Волновые процессы. Эффект Допплера. (Лекция 1)

1. ЛЕКЦИЯ 1

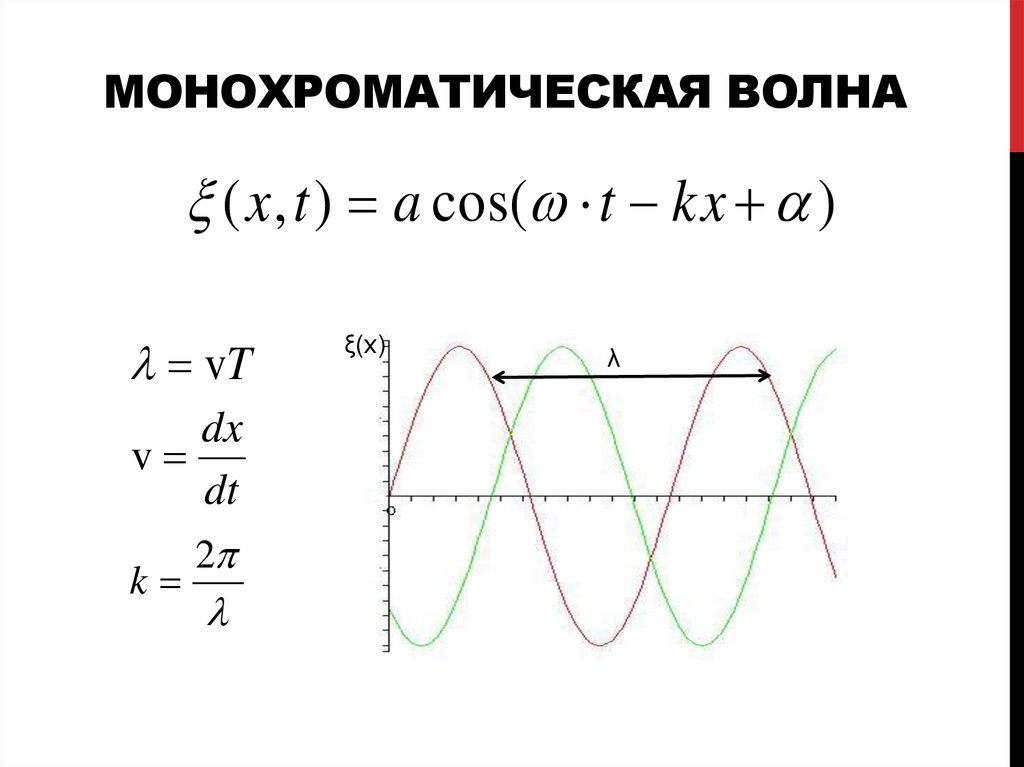
ВОЛНОВЫЕ ПРОЦЕССЫ

2. МОНОХРОМАТИЧЕСКАЯ ВОЛНА

( x , t ) a cos( t kx )
vT
dx
v
dt
2
k
ξ(x)
λ
t

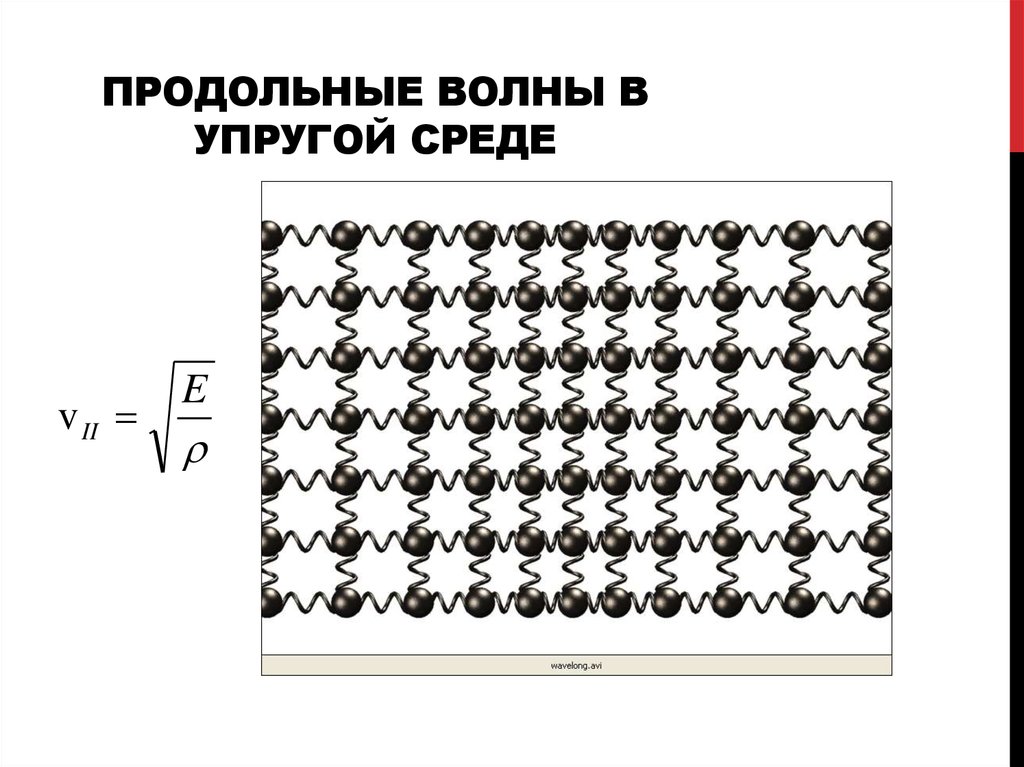
3. ПРОДОЛЬНЫЕ ВОЛНЫ В УПРУГОЙ СРЕДЕ

v II
E

4. ПОПЕРЕЧНЫЕ ВОЛНЫ В УПРУГОЙ СРЕДЕ

v
G

5. ВОЛНОВОЕ УРАВНЕНИЕ

1
2
2
v t
2
2
2
2
2 2 2
x y
z
Общее решение волнового
дифференциального уравнения
f ( r , t ) f1 ( t k r ) f 2 ( t k r )
Плоская
монохроматическая
волна
( r , t ) a cos( t k r )
Сферическая
монохроматическая
волна
a
( r , t ) cos( t k r )
r

6.

7. ВОЛНОВАЯ ПОВЕРХНОСТЬ

Геометрическое место точек, колеблющихся
в одинаковой фазе, называется волновой
поверхностью.
Волновой фронт (или фронт волны) –
геометрическое место точек, до которых
доходят колебания к данному моменту
времени t. Волновой фронт представляет
собой поверхность, которая отделяет
область пространства, уже вовлеченную в
волновой процесс, так называемую
волновую зону, от той части пространства,
куда колебания еще не дошли.

8. ЭНЕРГИЯ УПРУГОЙ ВОЛНЫ

2
2
1
2
W
v
V
2
x
t
1
2
2
w
a
2
Вектор Умова-Пойнтинга
Ф
W
S
S пл ощадь S пл ощадь t
S wv

9. ЭФФЕКТ ДОППЛЕРА

10. СУЩНОСТЬ ЯВЛЕНИЯ

Если источник волн движется относительно среды, то
расстояние между гребнями волн (длина волны) зависит от
скорости и направления движения. Если источник движется
по направлению к приёмнику, то есть догоняет испускаемую
им волну, то длина волны уменьшается. Если удаляется —
длина волны увеличивается.
v волны отн. неподв. источника и приёмника uисточника
0

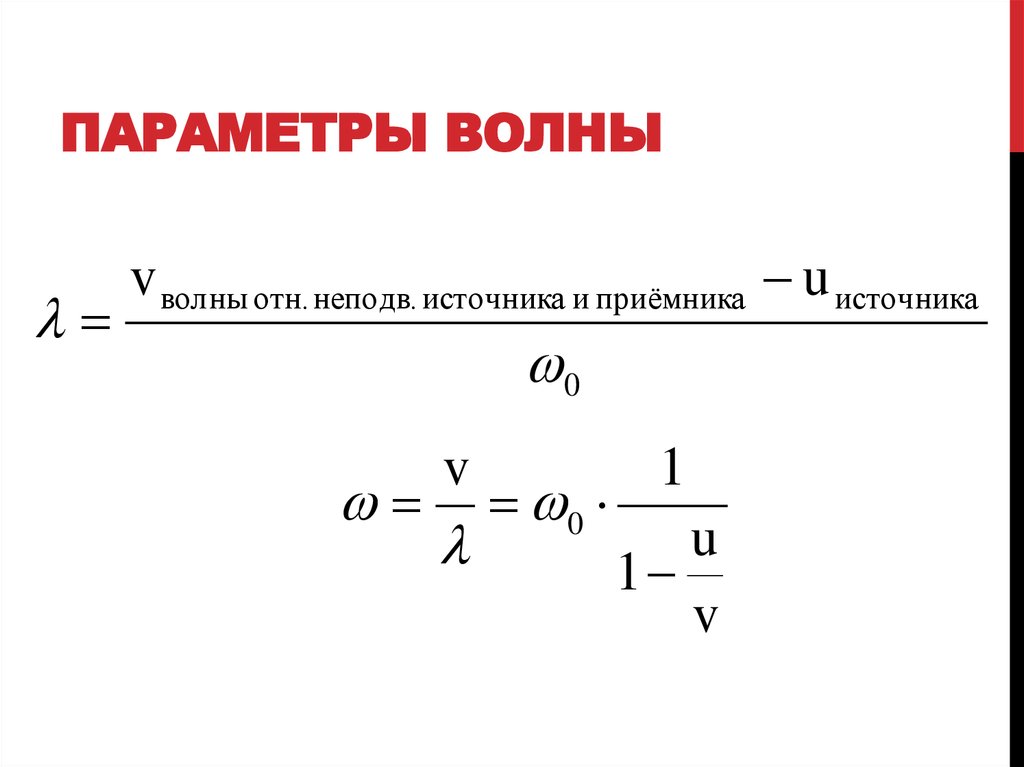
11. ПАРАМЕТРЫ ВОЛНЫ

v волны отн. неподв. источника и приёмника u источника
0
v
0
1
u
1
v

12. ЭФФЕКТ ДОППЛЕРА

13. СУЩНОСТЬ ЯВЛЕНИЯ

Если приёмник волн движется относительно среды, то
время между приходом гребней приходящих волн (период
колебаний в волне) зависит от скорости и направления
движения. Если приёмник движется по направлению к
источнику, то период увеличивается. Если удаляется —
уменьшается.
1
T T0
u
v
1
v

14. ПАРАМЕТРЫ ВОЛНЫ

1
T T0
u
v
1
v
v
u
f f 0 (1 )
v

15. ЭФФЕКТ ДОППЛЕРА

16. СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА

1
d
Г E dl dt S B dS
B dS 0
2
1
2
B
E
t
B 0
S
3
4
d
Г H dl j dS dt S D dS
D dS dV
S
V
3
4
D
H j
t
D

17. ЭЛЕКТРОМАГНИТНАЯ ВОЛНА

B
, E
t
2
, , E ( E ) E
E
0
если свободных зарядов нет, тт есть 0,
2
, , E E E

18. ЭЛЕКТРОМАГНИТНАЯ ВОЛНА

B
, E
t
B
D
, , B 0 , H 0 j
t
t
t
t
t
если j 0,
2
2
2
B
D
D
E
, 0 2 0 2 0 0 2
t
t
t
t

19. ВОЛНОВОЕ УРАВНЕНИЕ

E
E 2
c t 2
2
B
B 2 2
c t
2
c
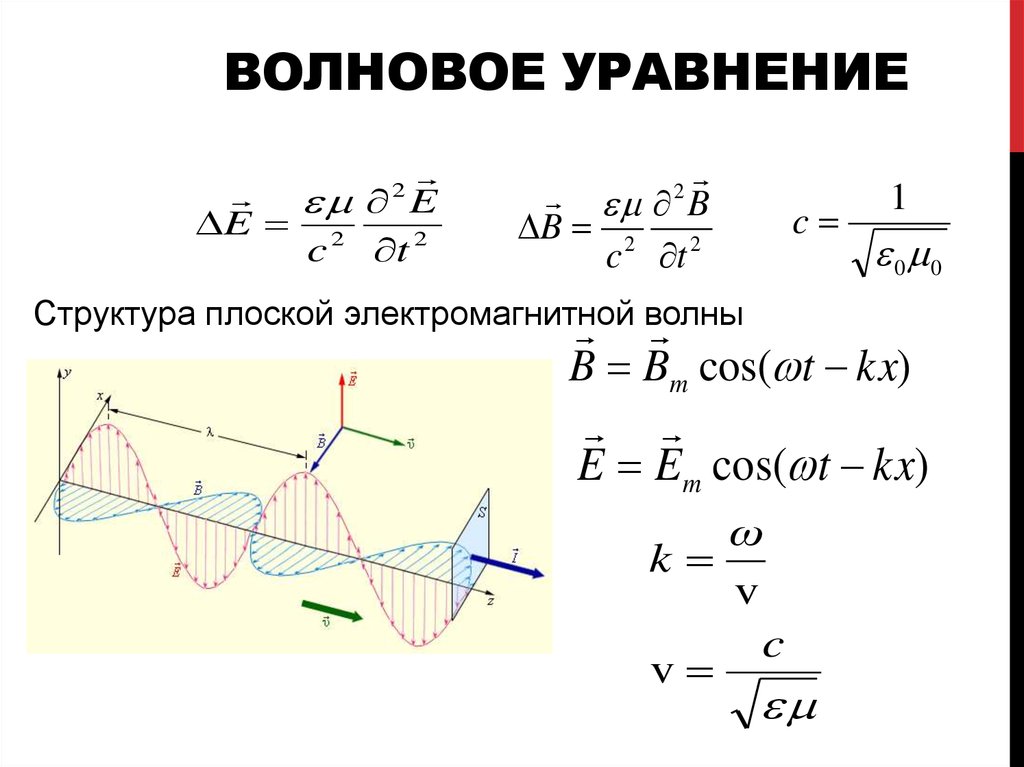
Структура плоской электромагнитной
волны
1
0 0
B Bm cos( t kx)
E Em cos( t kx)
ω
k
v
c
v

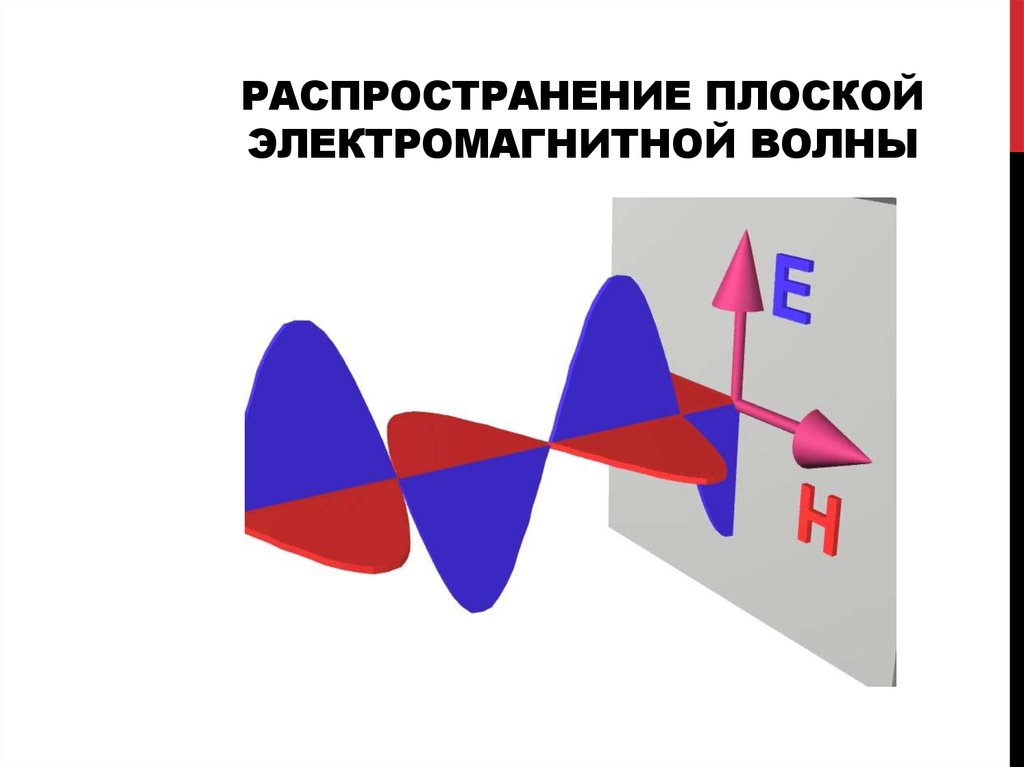
20. РАСПРОСТРАНЕНИЕ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

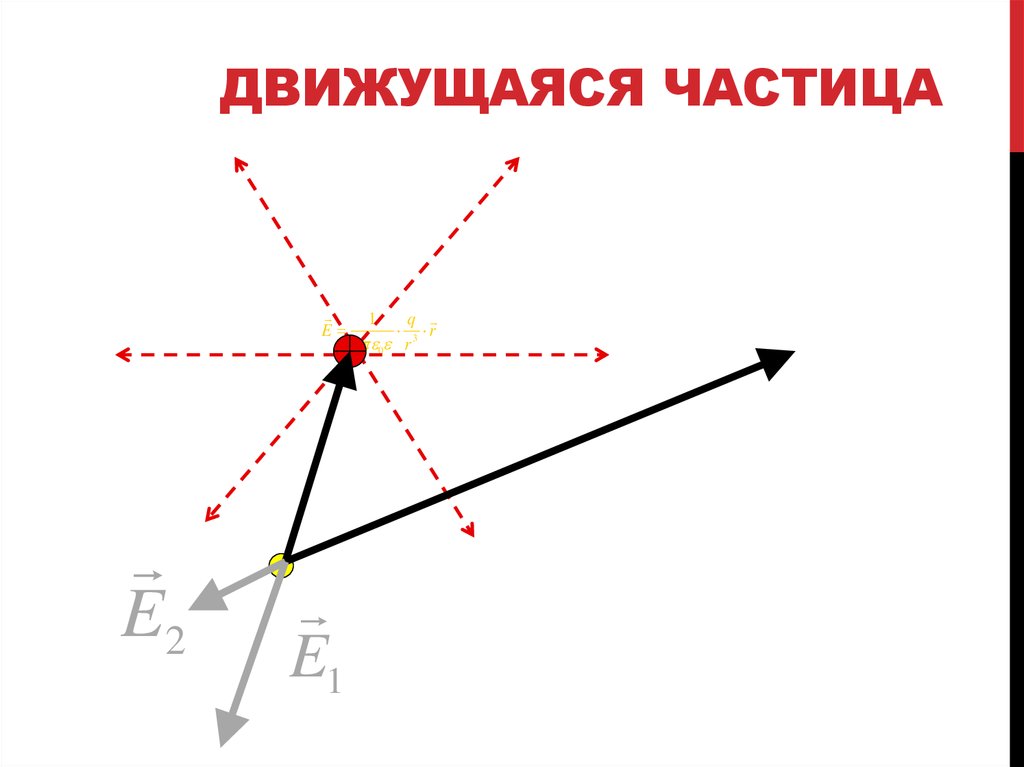
21. ДВИЖУЩАЯСЯ ЧАСТИЦА

E
E2
1
q
3 r
4 0 r
r1
E1
r2

22. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ДВИЖУЩИМСЯ ЗАРЯДОМ

vч
c

23. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ДВИЖУЩИМСЯ ЗАРЯДОМ

vч
c

24. ИЗЛУЧЕНИЕ ВАВИЛОВА-ЧЕРЕНКОВА

vч
c

25. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

E ( r , t ) E ( r ) cos( t k r )
2
2
0 E ( r , t ) 0 E ( r )
2
we
cos ( t k r )
2
2
2
0 E ( r , t )
0 E ( r ) 1
we
2
2
2
2

26. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

H ( r , t ) H ( r ) cos( t k r )
2
2
0 H ( r , t ) 0 H (r )
2
wm
cos ( t k r )
2
2
2
0 H (r , t )
0 H (r ) 1
2
2
2
2
wm

27. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

2
0 E ( r , t )
0 E 0 ( r ) 1
we
2
2
2
2
2
0 H (r , t )
0 H 0 (r ) 1
2
2
2
2
wm
w wm wm
2
0 E (r ) 0 H 0 (r ) 1
2
2
2
2
0

28. ВЕКТОР УМОВА-ПОЙНТИНГА

S w v
w we wm
we wm
v
c
0 E
2
2
0 H
2
2
0 E 0 H 0 0 EH
2
c
1
2
S E ,H
0 0
Вт
S
2
м

29. Интенсивность электромагнитных волн

I S
I 0 E 0 H
2
Вт
I 2
м
2

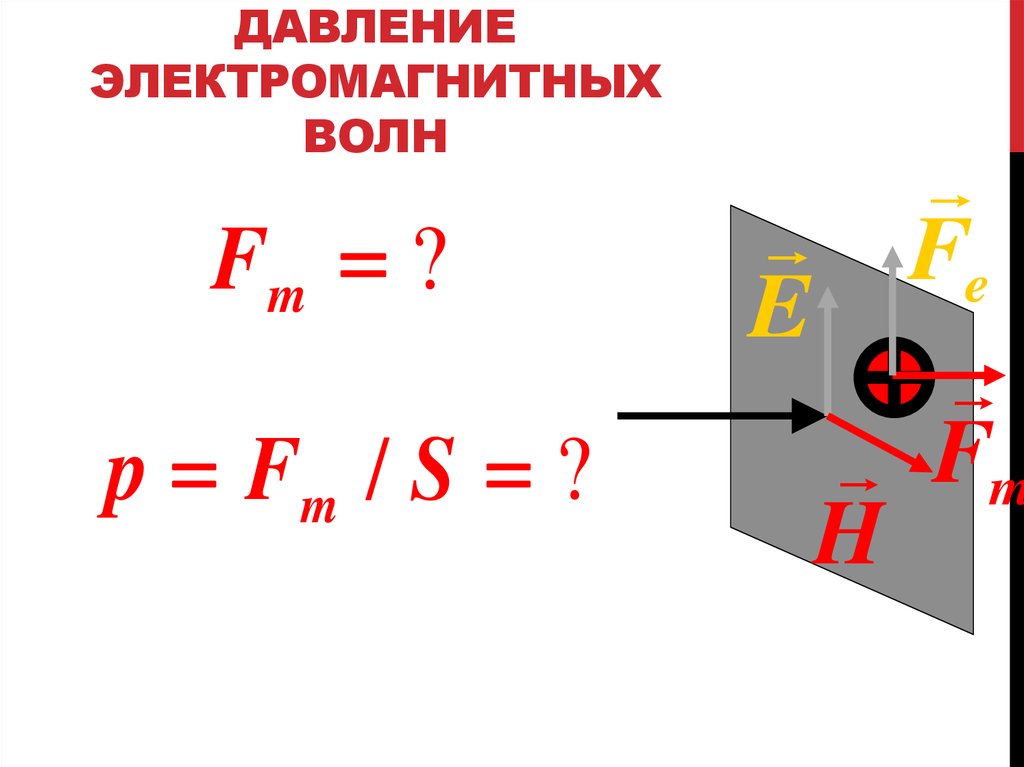
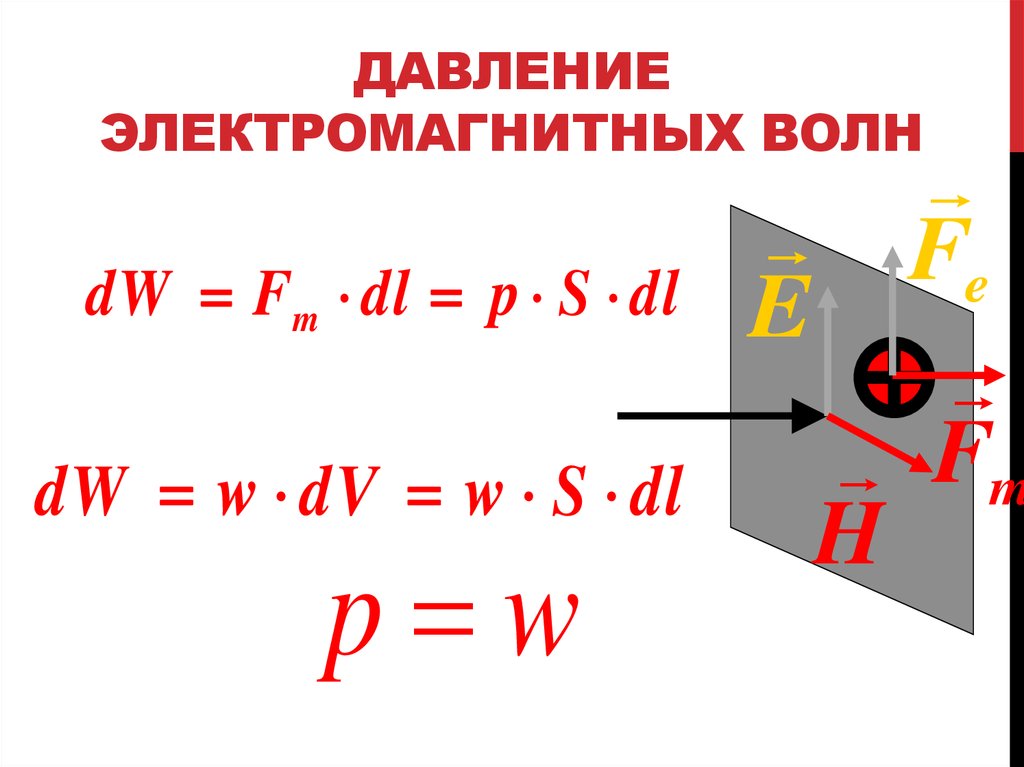
30. ДАВЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Fm ?
p Fm / S ?
Fe
E
Fm
H

31. ДАВЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

dW Fm dl p S dl
dW w dV w S dl
pp ww
Fe
E
Fm
H

32. ИМПУЛЬС ЭЛЕКТРОМАГНИТНЫХ ВОЛН

d ( Импульс )
F
dt
F p S w S
d ( Импульс ) w S dt
w S c dt
d ( Импульс)
c
dW
d ( Импульс)
c

33. ИМПУЛЬС ЭЛЕКТРОМАГНИТНЫХ ВОЛН

w S c dt dW
d ( Импульс )
c
c
W
( Импульс _ поля )
c
( Импульс _ системы) ( Импульсов _ тел) ( Импульсов _ полей )
( Импульса _ системы) ( Импульсов _ тел) ( Импульсов _ полей )

34. МАССА И ПЛОТНОСТЬ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

W
( Импульс _ поля )
c
( Импульс _ поля ) m v m c
W
w
m 2
2
c
c
W m c
2

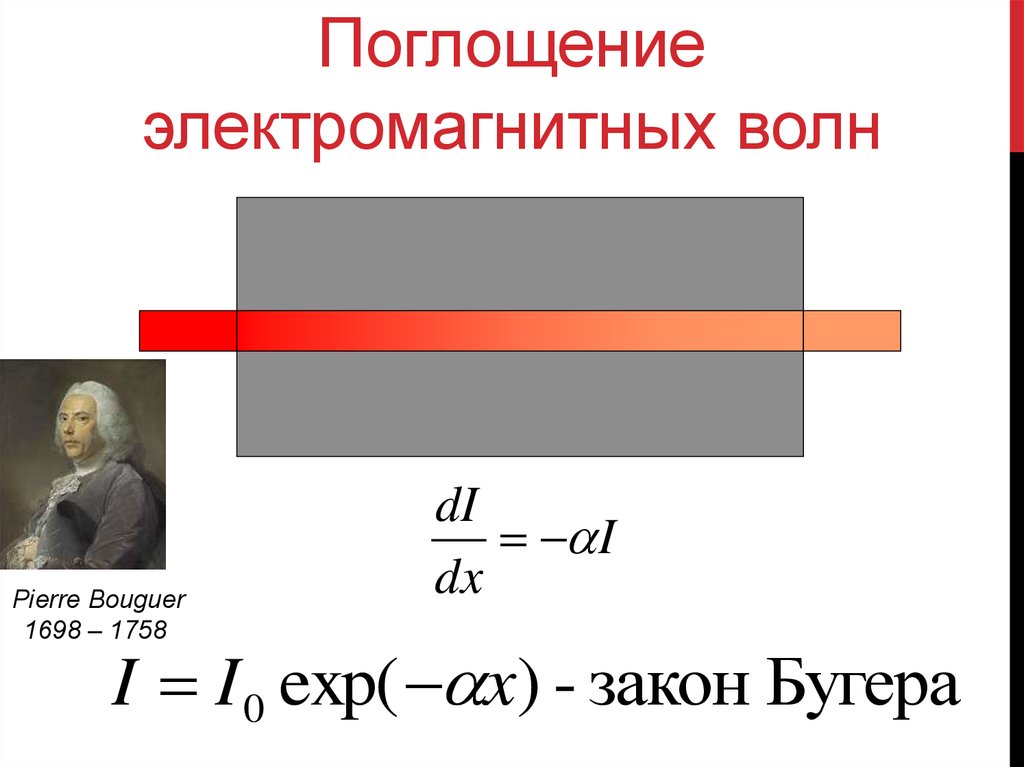
35. Поглощение электромагнитных волн

Pierre Bouguer
1698 – 1758
dI
I
dx
I I 0 exp( x) - закон Бугера

36. Рассеяние электромагнитных волн

John William Strutt,
3rd Baron Rayleigh
1698 – 1758
dI
I
dx
I I 0 exp( x) - закон Рэлея