Линейные цепи при несинусоидальных периодических токах

1. Линейные цепи при несинусоидальных периодических токах Подготовлено Степановым К.С.

2. Несинусоидальные токи

• Периодическими
несинусоидальными токами и
напряжениями называются токи и
напряжения, изменяющиеся во
времени по периодическому
несинусоидальному закону

3. Разложение периодических функций.  Характеристики несинусоидальных величин

Разложение периодических функций.
Характеристики несинусоидальных
величин
Для анализа процессов в линейных
электрических цепях при воздействии
на них несинусоидальных токов или
напряжений последние обычно
разлагаются в ряд Фурье. Формула
разложения имеет вид
k 1
k 1
f (t ) A0 ak cos k t bk sin k t A0 ck sin( k t k )

4. Разложение периодических функций. 

Разложение периодических функций.
T
1
Где A0 f (t )dt постоянная составляющая,
T0
c1 sin( t 1 ) первая (основная) гармоника,
ck sin( k t k ) высшие гармоники,
T
ck
2
2
ak bk
bk
arctg
ak
2
ak f (t ) cosk tdt
To
T
2
bk f (t ) sin k tdt
To

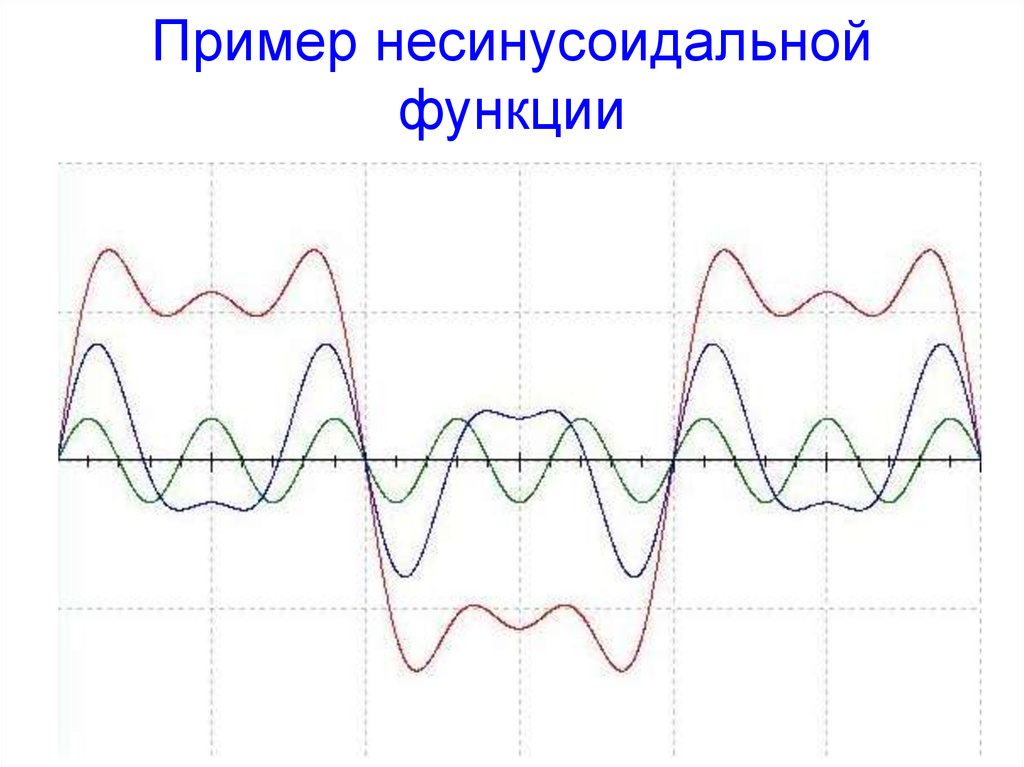
5. Пример несинусоидальной функции

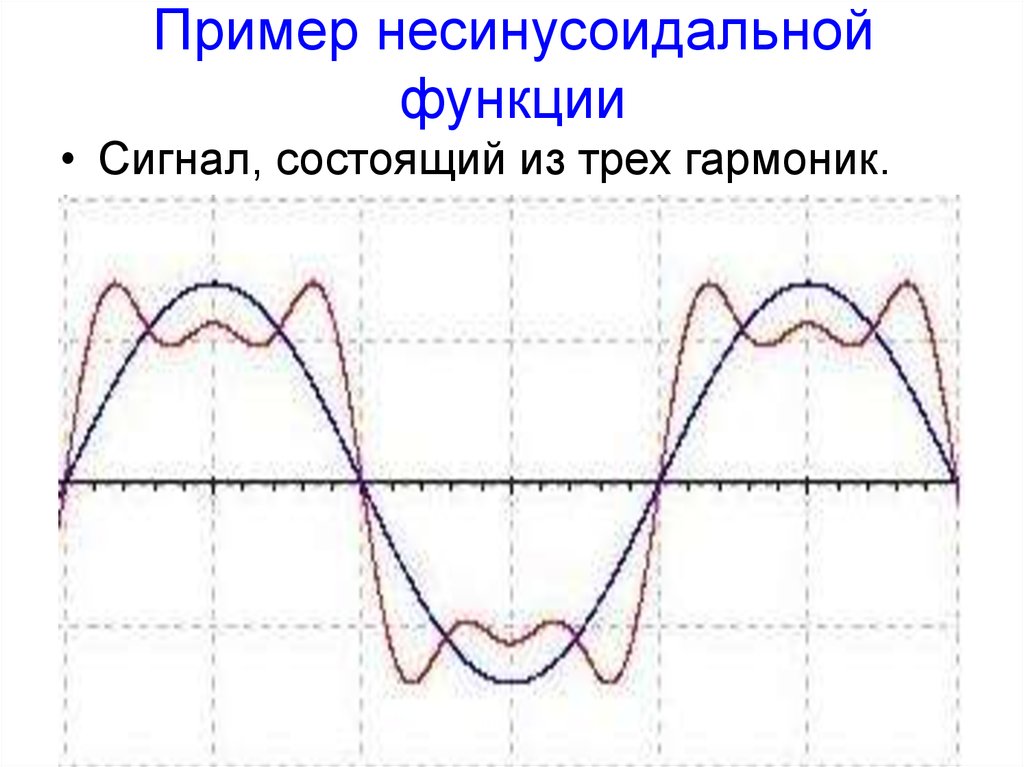
6. Пример несинусоидальной функции

• Сигнал, состоящий из трех гармоник.

7. типы периодических несинусоидальных функций

• 1. Кривые, симметричные относительно
оси абсцисс. К данному типу относятся
кривые с отсутствием постоянной
составляющей и удовлетворяющие
равенству
f (t ) f (t T / 2)

8. типы периодических несинусоидальных функций

2. Кривые, симметричные относительно
оси ординат, f (t ) f ( t ) т.е. в них
Отсутствуют постоянная и косинусные
составляющие, т.е., . bk 0
t

9. типы периодических несинусоидальных функций

3. Кривые, симметричные относительно
f (t ) f ( t )
начала координат
отсутствуют постоянная и косинусные
составляющие, т.е., A0 0 ak 0 .

10. Величины, характеризующие несинусоидальные токи

• Максимальное значение – I max
• Действующее значение
1T 2
I
i dt
T0
• Среднее по модулю значение
1T
I cp i dt
T0
• Среднее за период значение
T
1
I 0 idt
(постоянная составляющая)
T0

11. Величины, характеризующие несинусоидальные токи

• Коэффициент амплитуды
• Коэффициент формы
I max
êà
I
I
кф
I cp
• Коэффициент искажений
I1
ки
I
• Коэффициент гармоник к г
2
Ik
k 2
I1

12. Величины, характеризующие несинусоидальные токи

• Действующим значением периодической
несинусоидальной переменной называется
среднеквадратичное за период значение
величины:
T
1 2
I
i dt
T0

13. Величины, характеризующие несинусоидальные токи

• На практике действующее значение
переменной определяется на основе
информации о действующих значениях
конечного ряда гармонических.
1
2
I 2 I 02 I km
2 k 1
I
2
Ik
k 0

14. Мощность в цепях периодического несинусоидального тока

• Допустим, ток и напряжение являются
периодическими несинусоидальными
функциями:
u(t ) U km sin( k t k )
k 0
i(t ) I km sin( k t k )
k 0
1T
1T
P u (t ) i (t )dt U km sin k t k I km sin k t k dt
k 0
T0
T 0 k 0

15. Мощность в цепях периодического несинусоидального тока

• Среднее за период значение
произведения синусоидальных функций
различной частоты равно нулю, тогда
U km I km
P U0 I0
cos( k k ) U 0 I 0 U k I k cos k
2
k 1
k 1
k k k
Где
Реактивная мощность
Q
Qk
k 1
U k I k sin k
k 1

16. Мощность в цепях периодического несинусоидального тока

• Полная мощность
S UI
2
U
k
k 0
2
2
2
2
2
2
I
P
Q
T
P
Q
k
k 0
• где Т – мощность искажений,
определяемая произведениями
действующих значений разнопорядковых
гармонических тока и напряжения.

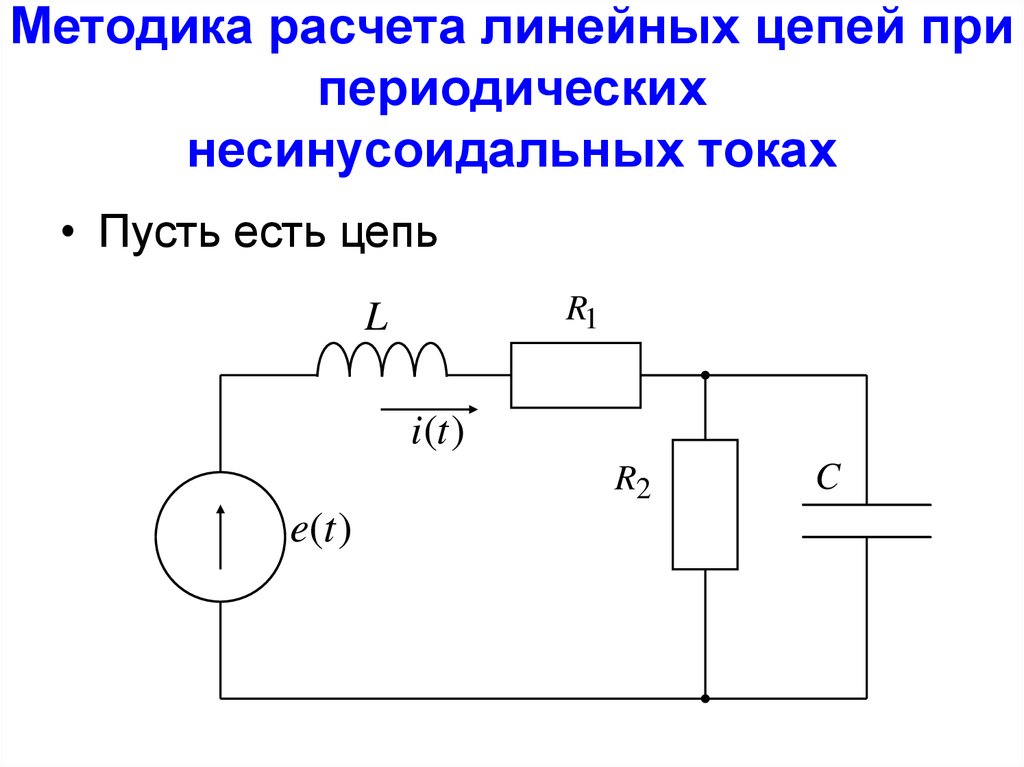
17. Методика расчета линейных цепей при периодических несинусоидальных токах

• Пусть есть цепь
R1
L
i(t )
R2
e(t )
C

18. Методика расчета линейных цепей при периодических несинусоидальных токах

Определить мгновенные значения токов и
напряжений.
Для этого используется следующий алгоритм:
• 1. ЭДС и токи источников раскладываются
в ряды Фурье.
• 2. ЭДС и токи источников раскладываются
в ряды Фурье.
• 3. Искомые величины определяются как
алгебраические суммы соответствующих
гармонических.

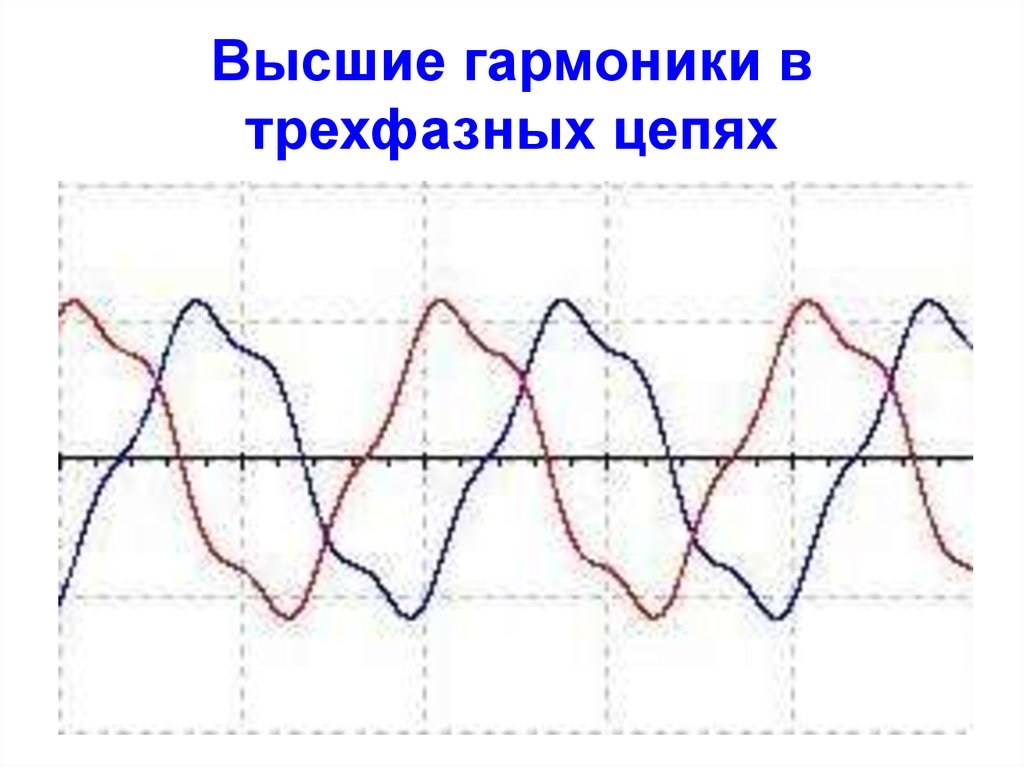
19. Высшие гармоники в трехфазных цепях

Рассмотрим особенности работы
трехфазных систем, обусловленные
наличием гармоник, кратных трем.
:

20. Высшие гармоники в трехфазных цепях

• Если фазы генератора соединены в
треугольник, то при фазных
несинусоидальных ЭДС, сумма
ЭДС, действующих в контуре, не
равна нулю, а определяется
гармониками, кратными трем. Эти
гармоники вызывают в замкнутом
треугольнике генератора ток, даже
когда его внешняя цепь (нагрузка)
разомкнута

21. Высшие гармоники в трехфазных цепях

22. Высшие гармоники в трехфазных цепях

23.

V2 3
U2
-
4
38 Vrms
50 Hz
0°
+
0.980m
0.982m
A
-
+
A
AC 1e-009 W
2
V3
U3
AC 1e-009 W
38 Vrms
50 Hz
240°
7 V4
1 V5
5 Vrms
200 Hz
0°
5 Vrms
200 Hz
240°
5
8
V6
5 Vrms
200 Hz
120°
6 V1
0
38 Vrms
50 Hz
120°
U1
+
0.982m
A
AC 1e-009 W

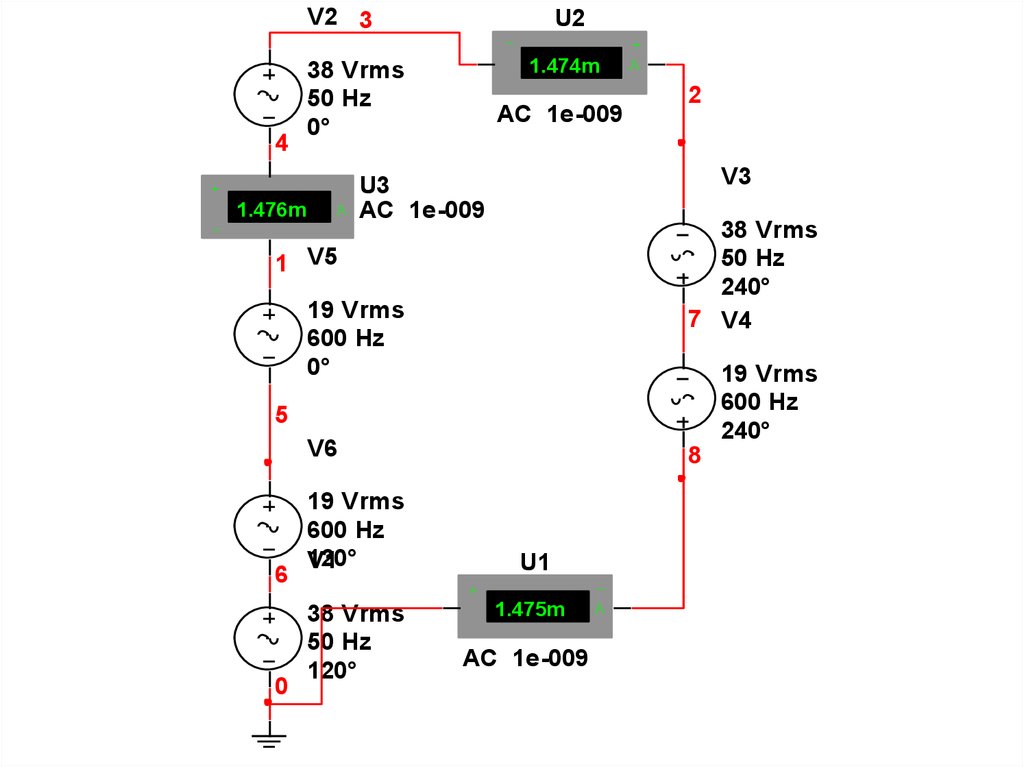
24.

V2 3
U2
-
4
+
1.476m
1.474m
38 Vrms
50 Hz
0°
A
-
+
A
AC 1e-009 W
2
V3
U3
AC 1e-009 W
38 Vrms
50 Hz
240°
7 V4
1 V5
19 Vrms
600 Hz
0°
19 Vrms
600 Hz
240°
5
V6
6
0
8
19 Vrms
600 Hz
120°
V1
U1
+
38 Vrms
50 Hz
120°
1.475m
A
AC 1e-009 W

25.

V2 3
U2
-
4
+
0.370m
0.372m
38 Vrms
50 Hz
0°
A
-
+
A
AC 1e-009 W
2
V3
U3
AC 1e-009 W
38 Vrms
50 Hz
240°
7 V4
1 V5
0 Vrms
600 Hz
0°
0 Vrms
600 Hz
240°
5
V6
6
0
8
0 Vrms
600 Hz
120°
V1
U1
+
38 Vrms
50 Hz
120°
0.372m
A
AC 1e-009 W

26.

V2 3
U2
-
4
+
4.011u
4.049u
38 Vrms
50 Hz
0°
A
-
+
A
AC 1e-009 W
2
V3
U3
AC 1e-009 W
38 Vrms
50 Hz
240°
7 V4
1 V5
0 Vrms
600 Hz
0°
0 Vrms
600 Hz
240°
5
V6
6
0
0 Vrms
600 Hz
120°
V1
38 Vrms
50 Hz
120°
8
U4
+
1.149p
AC 10M W
V

27.

V2 3
U2
-
4
+
4.753u
5.652u
38 Vrms
50 Hz
0°
A
-
+
A
AC 1e-009 W
2
V3
U3
AC 1e-009 W
38 Vrms
50 Hz
240°
7 V4
1 V5
20 Vrms
600 Hz
0°
20 Vrms
600 Hz
240°
5
V6
6
0
20 Vrms
600 Hz
120°
V1
38 Vrms
50 Hz
120°
8
U4
+
7.738p
AC 10M W
V

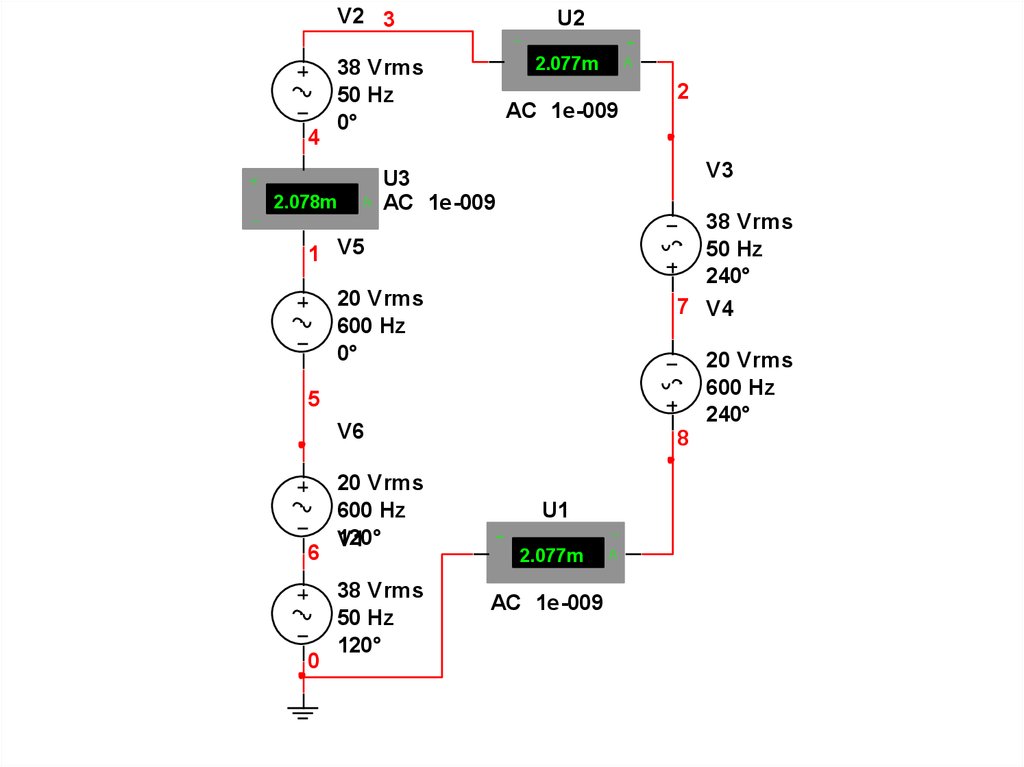
28.

V2 3
U2
-
4
2.078m
2.077m
38 Vrms
50 Hz
0°
+
A
-
+
A
AC 1e-009 W
2
V3
U3
AC 1e-009 W
38 Vrms
50 Hz
240°
7 V4
1 V5
20 Vrms
600 Hz
0°
20 Vrms
600 Hz
240°
5
V6
6
0
20 Vrms
600 Hz
120°
V1
38 Vrms
50 Hz
120°
8
U1
+
2.077m
A
AC 1e-009 W

29.

30. Пример расчёта

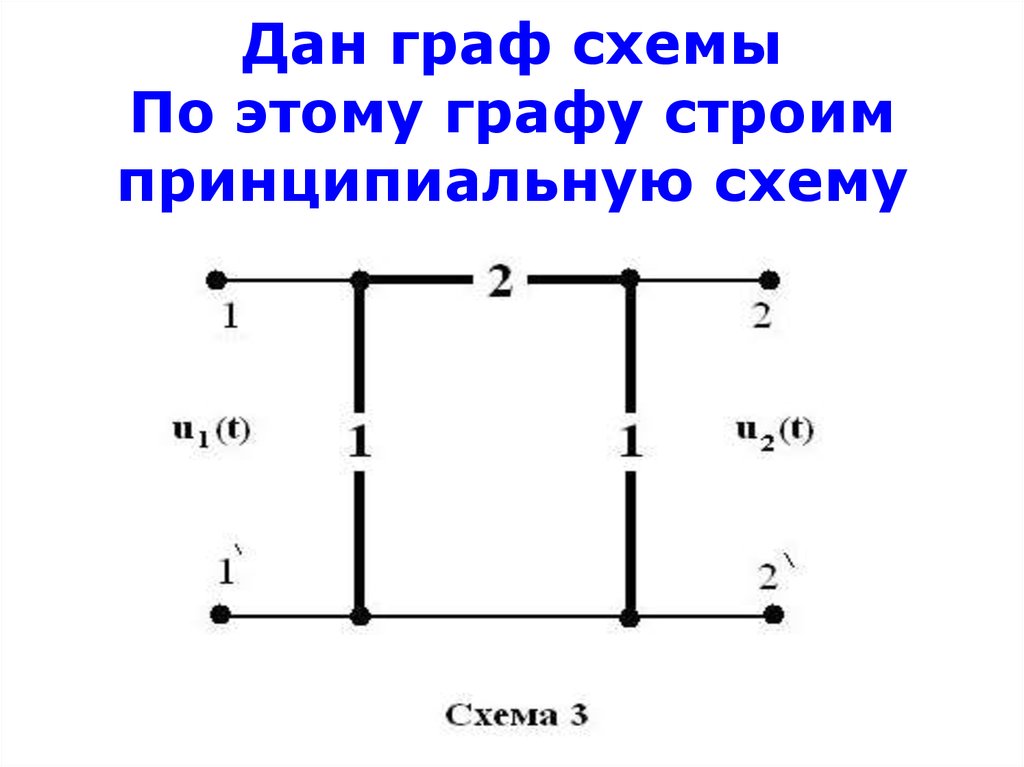
1. По графу составить принципиальную схему
2. Вести расчёт для каждой гармоники
отдельно
3. Алгебраически сложить полученные
значения мгновенных величин.
4. Построить графики требуемых функций

31. Дан граф схемы По этому графу строим принципиальную схему

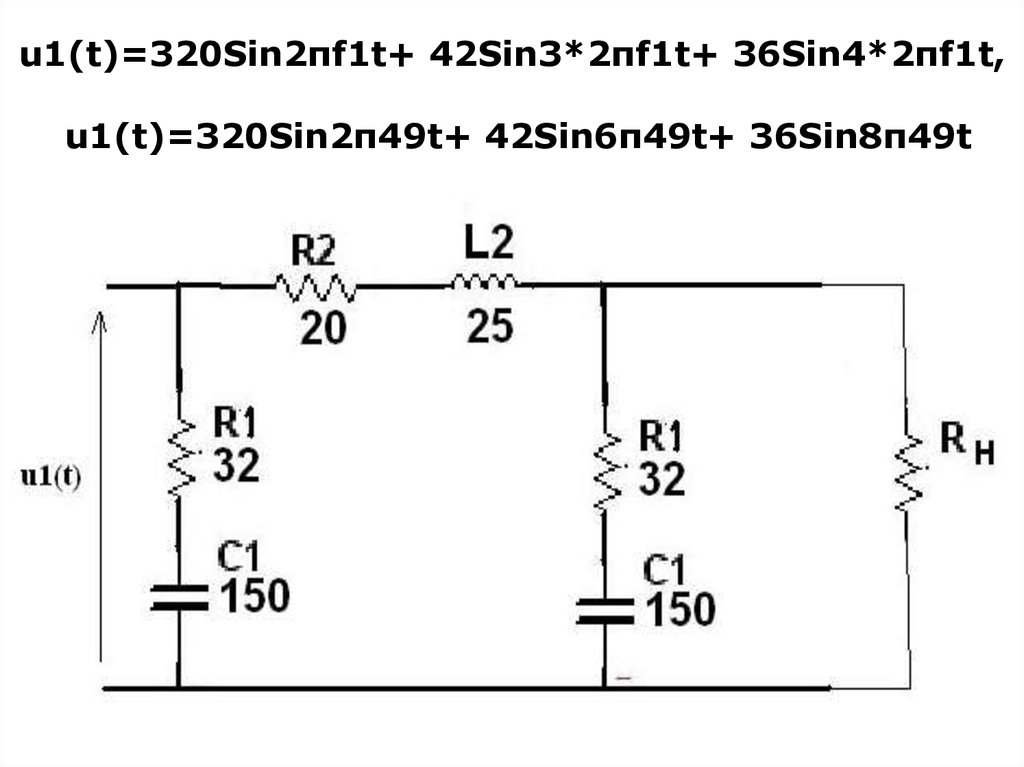
32. u1(t)=320Sin2πf1t+ 42Sin3*2πf1t+ 36Sin4*2πf1t, u1(t)=320Sin2π49t+ 42Sin6π49t+ 36Sin8π49t

33. Так как первая ветвь не влияет на значение u2(t), то её можно исключить

34. Определяется комлекс напряжения для каждой гармоники

• Тогда выходное напряжение определяется
по формуле
• где
1
Z1 R 1 j
k C
Z2 R 2 j k L2
U
Z
1
1
U2
Z2 Z1
k k 2 f1

35.

• Переводится комплексное
значение в форму мгновенного
значения и затем гармоники
складываются алгебраически.
• В комплексной форме
гармоники складывать
нельзя

36.

Благодарю за внимание