Способы преобразования чертежа. Способ вращения вокруг прямой уровня

1. Начертательная геометрия Семинар №8 Способы преобразования чертежа. Способ вращения вокруг прямой уровня. Подготовили: Данилова

Разработали: Данилова У.Б., Елисеева О.И.

2. Вращение вокруг горизонтали

А
а’
1
А’
в’
O
_
а’
Ось вращения горизонталь
Плоскость
вращения
Центр вращения
Радиус вращения
2
_
в’
_
А’
Разработали: Данилова У.Б., Елисеева О.И.

3.

Задача 62. Построить проекции биссектрисы угла
А, применив вращение вокруг горизонтали.
DZAO
h’’
1’’
2’’
В’’
_
а’
O’’
_
b’
1’
2’
В’ f
Ао
O’
_
А’
aвр.
1. Ось вращения - h - горизонталь плоскости,
заданной пересекающимися прямыми а и в
2. a-Плоскость вращения точки А
3. O – центр вращения точки А
4. АО – радиус вращения точки А
5. Вращаем точку А0 до плоскости вращения
6. Точки 1 и 2 расположены на оси вращения,
значит и повернутые они находятся там же,
тогда угол f – это натуральная величина угла
А.
7. Делим угол пополам – находим биссектрису
повернутого угла.
8. Точка пересечения биссектрисы с
горизонталью будет и ее горизонтальной
проекцией. Тогда горизонтальная проекция
биссектрисы – A’В’
9. A’’В’’ – фронтальная проекция биссектрисы.
Разработали: Данилова У.Б., Елисеева О.И.

4.

Задача 63. Определить угол между прямыми а и в,
применив вращение вокруг фронтали.
_ aвр.
А’
2’’
1’’ O’’
_
а1’’
а1 ’
= f’
Ао
А’’
O’
1’
DyAO
А’
2’
_
b’’
1. Прямые а и в – скрещивающиеся. Чтобы
найти угол между ними нужно параллельно
одной из прямых задать плоскость, в которой
заданная и параллельная второй заданной
прямой будут пересекаться. Точка пересечения
– А.
2. Ось вращения - f - фронталь плоскости,
заданной пересекающимися прямыми а1 и в
3. a-Плоскость вращения точки А
4. O – центр вращения точки А
5. IАОI – радиус вращения точки А
6. Вращаем точку А0 до плоскости вращения
7. Точки 1 и 2 расположены на оси вращения,
значит и повернутые они находятся там же,
тогда угол f – это натуральная величина угла
А.
Разработали: Данилова У.Б., Елисеева О.И.

5.

Задача 66-1. Определить угол между прямой а и
плоскостью b, применив вращение вокруг прямой уровня.
Из точки А, принадлежащей прямой а,
задаем нормаль n к плоскости b .
2.
Точка N –точка пересечения нормали с
плоскостью b.
3.
Точка К – точка пересечения прямой а с
плоскостью b.
4.
f’, f’’ - проекции искомого угла
5. Ось вращения - h - горизонталь
плоскости, заданной пересекающимися
прямыми а и n совпадает с нормалью n,
т.к. b горизонтально-проецирующая
6. a-Плоскость вращения точки К
7. O – центр вращения точки К
8. IКОI – радиус вращения точки К
9. Вращаем точку К0 до плоскости
вращения
10. Точки А и N расположены на оси
вращения, значит и повернутые они
находятся там же, тогда угол f– это
натуральная величина угла.
1.
N’’=O’’
А’’
n’’=h’’
f’’
DZKO
K’’
_
K’ aвр.
f
А’
f’
N’=O’
K’
=h’
Kо
Разработали: Данилова У.Б., Елисеева О.И.

6.

Задача 66-2. Определить угол между прямой а и
плоскостью b, применив вращение вокруг прямой уровня.
aвр.
_
n’’
А’’
1’’
f O’’
d
Ао
2’’
_
А’
f’
O’
DyAO
1’
А’
2’
_
а’’
1. Из точки А, принадлежащей прямой а
задаем нормаль n к плоскости b.
2. Ось вращения - f - фронталь плоскости,
заданной пересекающимися прямыми а и n
3. a-Плоскость вращения точки А
4. O – центр вращения точки А
5. IАОI – радиус вращения точки А
6. Вращаем точку А0 до плоскости
вращения
7. Точки 1 и 2 расположены на оси
вращения, значит и повернутые они
находятся там же, тогда угол d– это
натуральная величина угла А.
8. Достраиваем угол до 90 – получаем
натуральную величину угла f.
0
Разработали: Данилова У.Б., Елисеева О.И.

7.

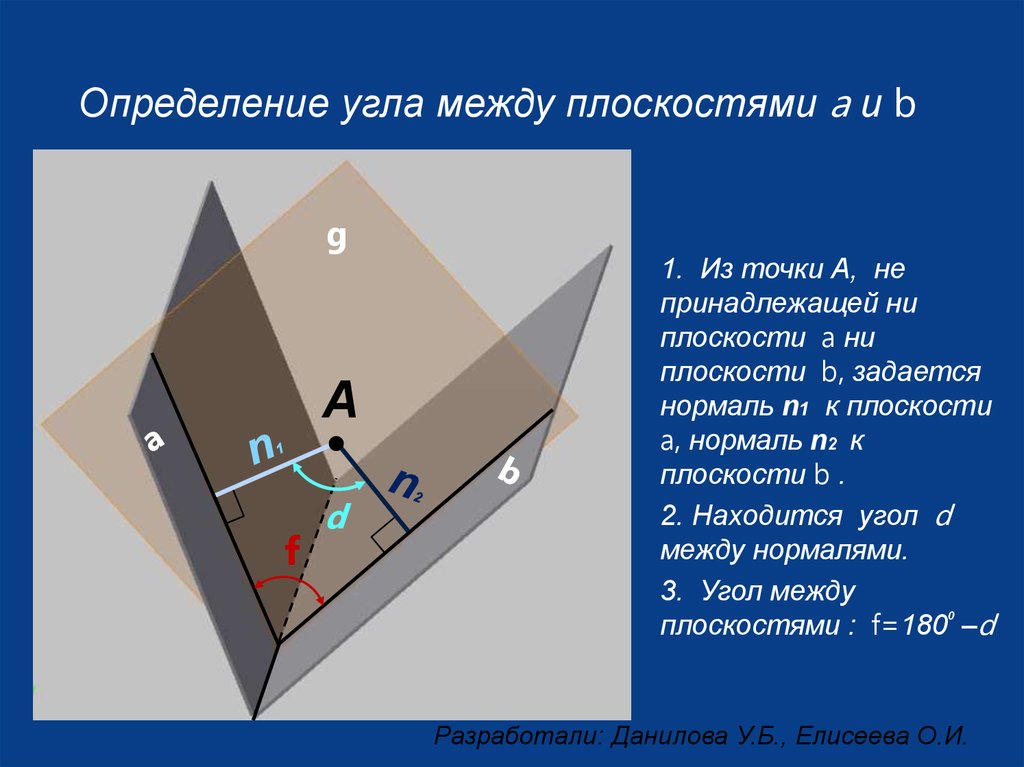
Определение угла между плоскостями a и b
g
А
f
d
1. Из точки А, не
принадлежащей ни
плоскости a ни
плоскости b, задается
нормаль n1 к плоскости
a, нормаль n2 к
плоскости b .
2. Находится угол d
между нормалями.
3. Угол между
0
плоскостями : f=180 –d
Разработали: Данилова У.Б., Елисеева О.И.

8.

Задача 67. Определить угол между плоскостями a и
b, применив вращение вокруг прямой уровня.
А’’
h’’
DZ
O’’
1’’
2’’
AO
aвр.
2’
1’
O’
d
f
Ао
А’
_
А’
1. Из точки А, не принадлежащей ни
плоскости a ни плоскости b, задаем
нормаль n1 к плоскости a, нормаль n2 к
плоскости b .
2. Ось вращения - h - горизонталь
плоскости, заданной пересекающимися
прямыми n1 и n2
3. a-Плоскость вращения точки А
4. O – центр вращения точки А
5. IАОI – радиус вращения точки А
6. Вращаем точку А0 до плоскости
вращения
7. Точки 1 и 2 расположены на оси
вращения, значит и повернутые они
находятся там же, тогда угол d– это
натуральная величина угла А.
8. Достраиваем угол до 180 – получаем
натуральную величину угла f.
0
Разработали: Данилова У.Б., Елисеева О.И.