Похожие презентации:
Способы преобразования чертежа
1. Начертательная геометрия Семинар №7 Способы преобразования чертежа. Подготовили: Данилова У.Б., Елисеева О.И. Московский
Разработали: Данилова У.Б., Елисеева О.И.2.
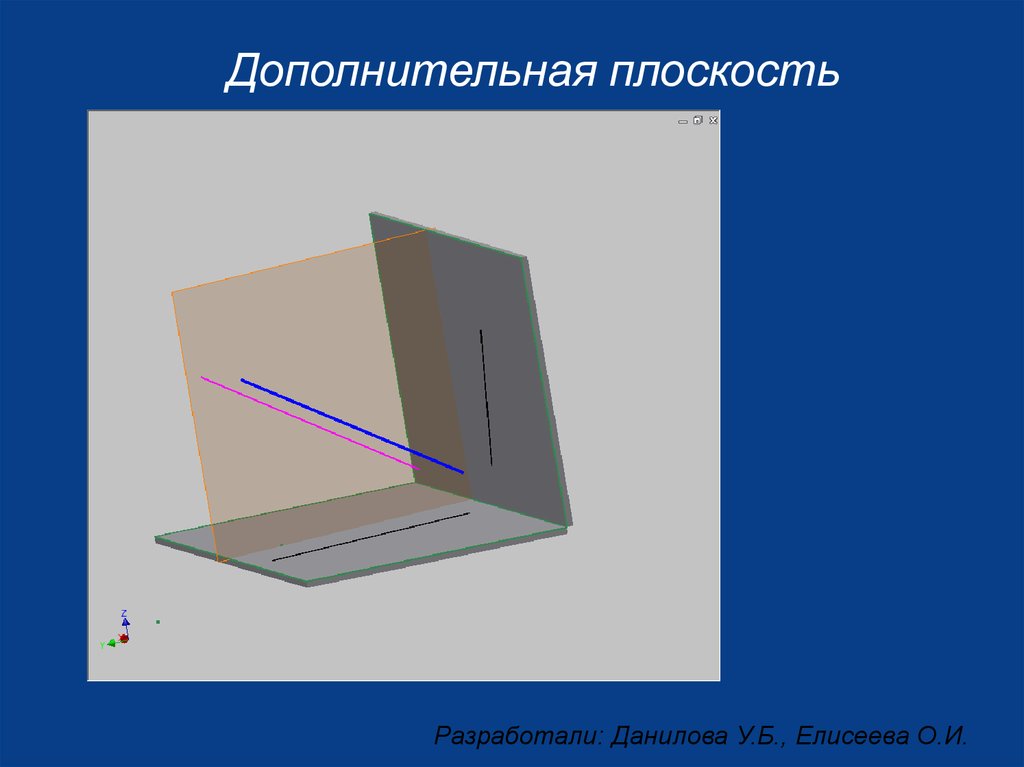
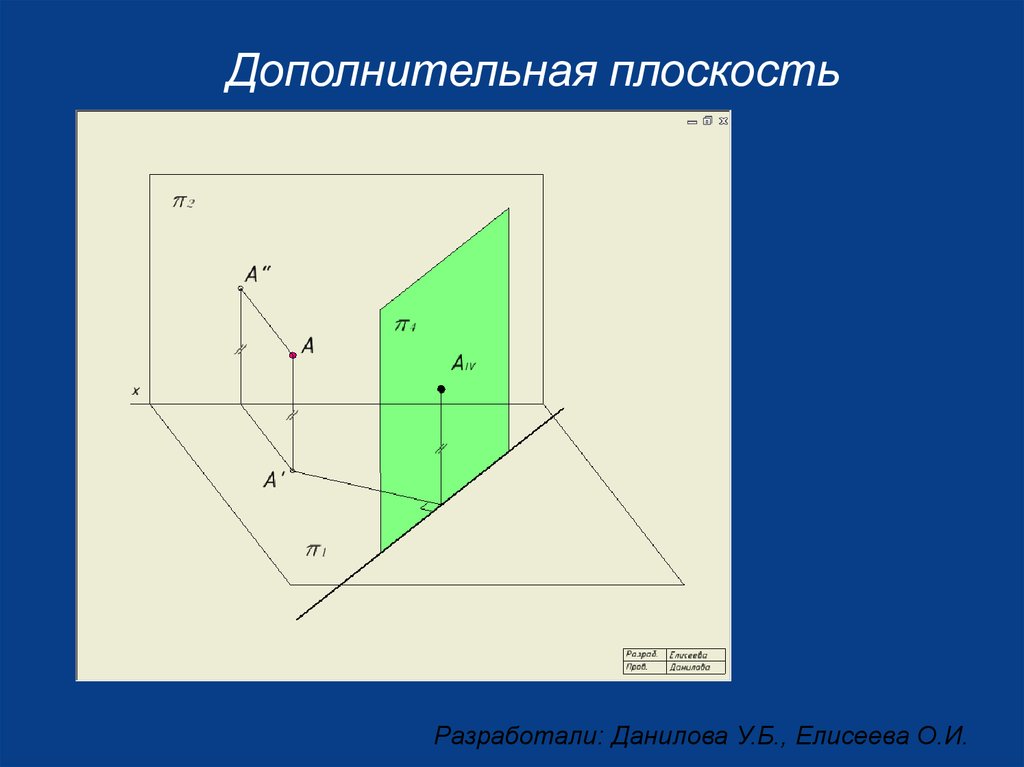
Дополнительная плоскостьРазработали: Данилова У.Б., Елисеева О.И.
3.
Дополнительная плоскостьРазработали: Данилова У.Б., Елисеева О.И.
4.
Задача 51. Заменой плоскостей проекций преобразоватьчертеж отрезка АВ так, чтобы в новой системе
плоскостей проекций отрезок занял проецирующее
положение.
1. Задаем новую плоскость p4
параллельно одной из проекций
отрезка.
2 . Задаем еще одну плоскость
p5 перпендикулярно проекции
отрезка.
zВ
zA
p2
p1
p1
p4
AVI
BVI
AV=BV
Разработали: Данилова У.Б., Елисеева О.И.
5.
Задача 54. Построить натуральный вид сечения призмыплоскостью a , используя способ замены плоскостей
проекций.
1 IV
6 IV
5 IV
2 IV
Cечение на чертеже.
4 IV
3 IV
1 II
2 II=6 II
3 II =5
II
4 II
p2
p1
2I
y2 =y3
3I
y1=y4
y6 =y5
1
4I
I
6I
5I
Разработали: Данилова У.Б., Елисеева О.И.
6.
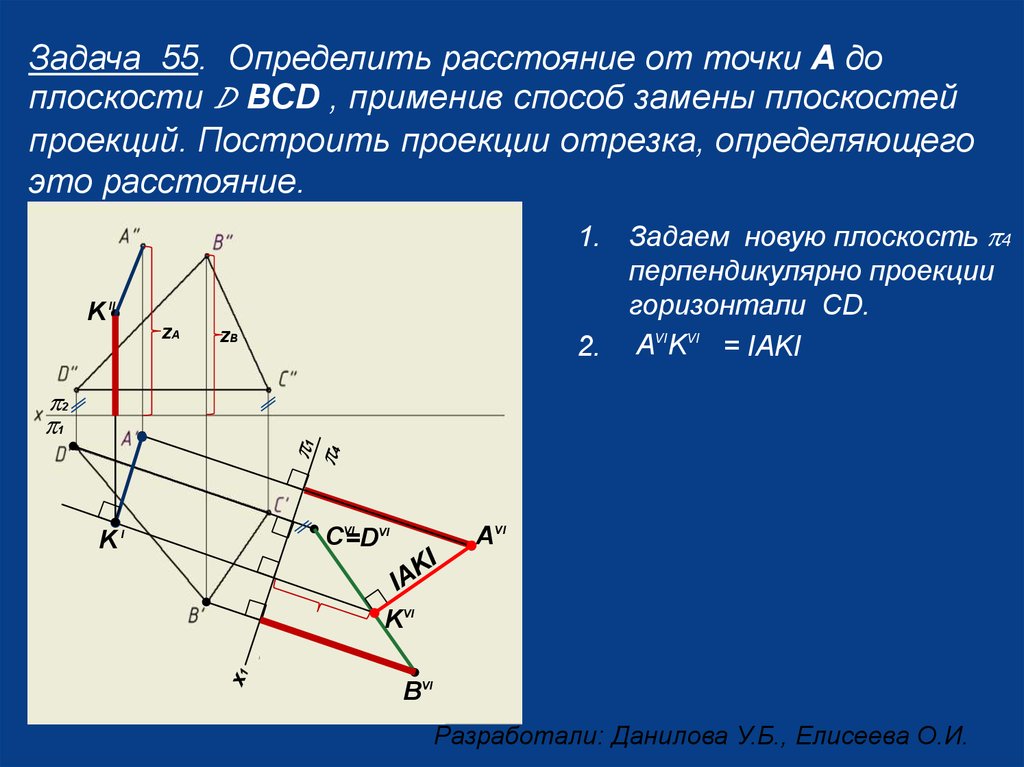
Задача 55. Определить расстояние от точки А доплоскости D ВСD , применив способ замены плоскостей
проекций. Построить проекции отрезка, определяющего
это расстояние.
K II
zA
1. Задаем новую плоскость p4
перпендикулярно проекции
горизонтали CD.
2. AVIKVI = IAKI
zВ
p2
p1
KI
СVI=DVI
AVI
KVI
BVI
Разработали: Данилова У.Б., Елисеева О.И.
7.
Задача 56. Построить проекции центра окружности,вписанной в треугольник АВС, используя способ замены
плоскостей проекций .
O II
zA =zВ
С II
p2
p1
OI
AIV=ВIV
1.Задаем новую плоскость p4:
p4 bA’ B’
2 .Задаем плоскость p5:
p5 II DАВС.
3 .(.) О – точка пересечения
биссектрис DАВС.
OVI
ВV
С VI
OV
СV
AV
Разработали: Данилова У.Б., Елисеева О.И.
8.
Задача 57. Определить величину двухгранного угламежду плоскостями треугольников АВС и АВD,
применив способ замены плоскостей проекций .
Разработали: Данилова У.Б., Елисеева О.И.
9.
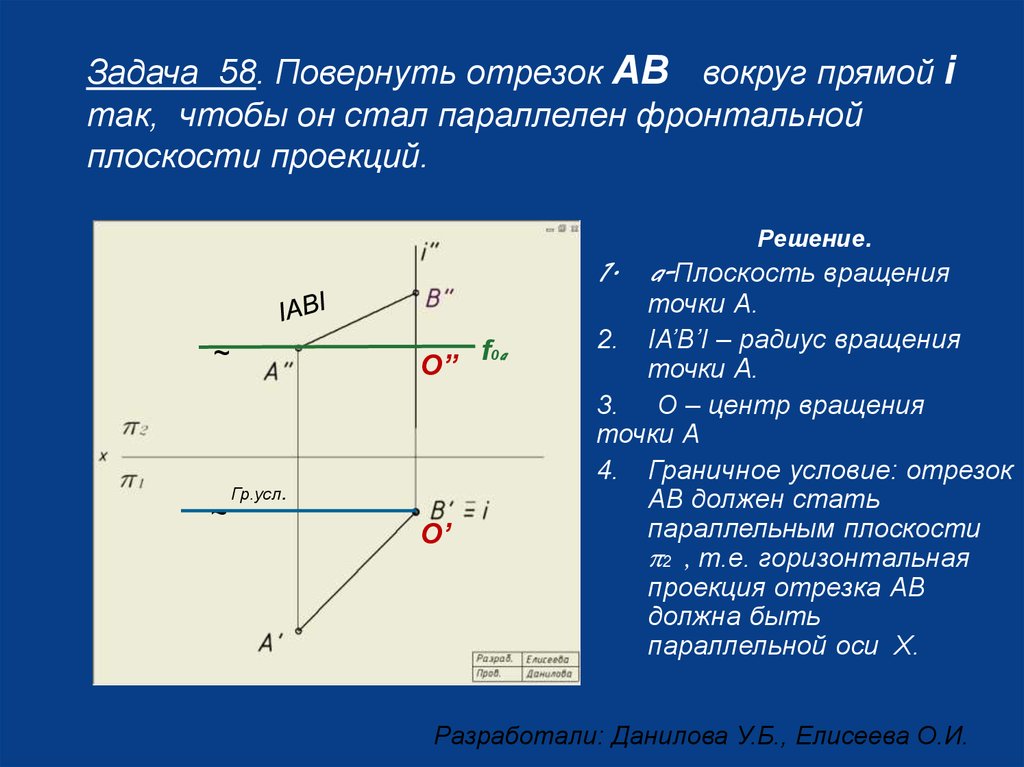
Задача 58. Повернуть отрезок АВ вокруг прямой iтак, чтобы он стал параллелен фронтальной
плоскости проекций.
1.
_
А’’
O’’
2.
3. O – центр вращения точки
Гр.усл.
_
А’
f0a
Решение.
a-Плоскость вращения
точки А.
IА’В’I – радиус вращения
точки А.
O’
А
4.
Граничное условие: отрезок
АВ должен стать
параллельным плоскости
p2 , т.е. горизонтальная
проекция отрезка АВ
должна быть
параллельной оси Х.
Разработали: Данилова У.Б., Елисеева О.И.
10.
Задача 58. Повернуть отрезок АВ вокруг прямой iтак, чтобы он стал параллелен фронтальной
плоскости проекций.
1.
~
O’’
Гр.усл.
O’
f0a
Решение.
a-Плоскость вращения
точки А.
2. IА’В’I – радиус вращения
точки А.
3. O – центр вращения
точки А
4. Граничное условие: отрезок
АВ должен стать
параллельным плоскости
p2 , т.е. горизонтальная
проекция отрезка АВ
должна быть
параллельной оси Х.
Разработали: Данилова У.Б., Елисеева О.И.
~
11.
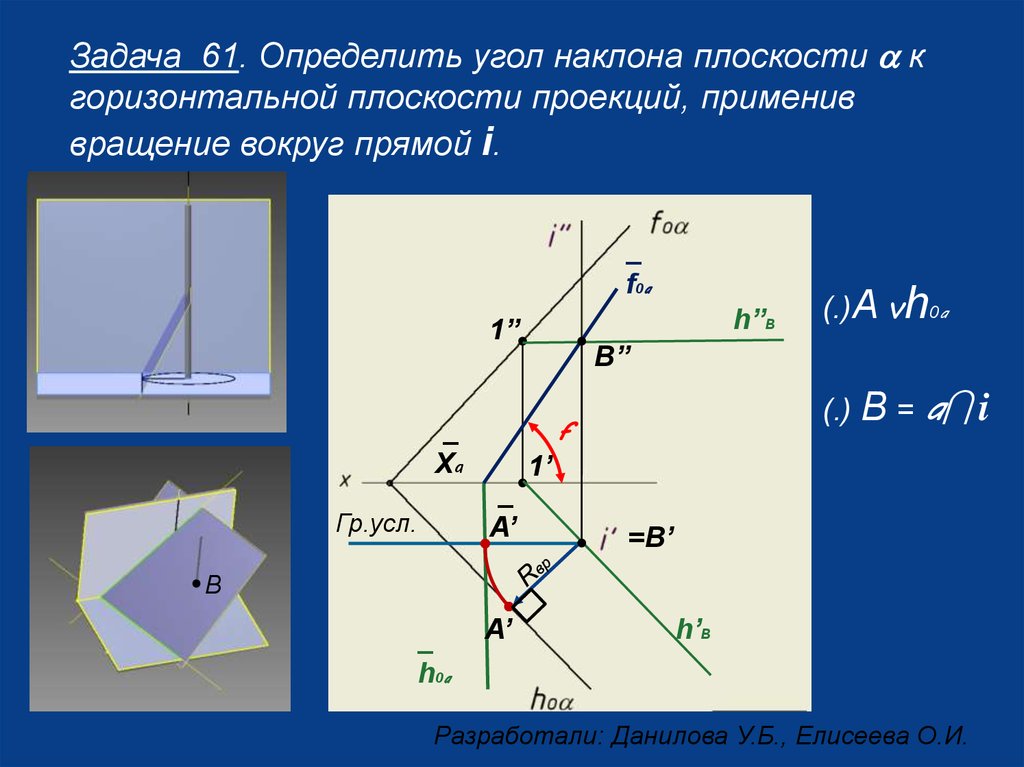
Задача 61. Определить угол наклона плоскости a кгоризонтальной плоскости проекций, применив
вращение вокруг прямой i.
_
f0a
h’’В
1’’
(.) В = aI
f
_
Xa
1’
_
А’
Гр.усл.
В’’
(.)А vh0a
=В’
В
_
h0a
А’
h’В
Разработали: Данилова У.Б., Елисеева О.И.
i






 Инженерная графика
Инженерная графика








