Виды изгибов. (Лекция 7)

1. Лекция № 7

1

2.

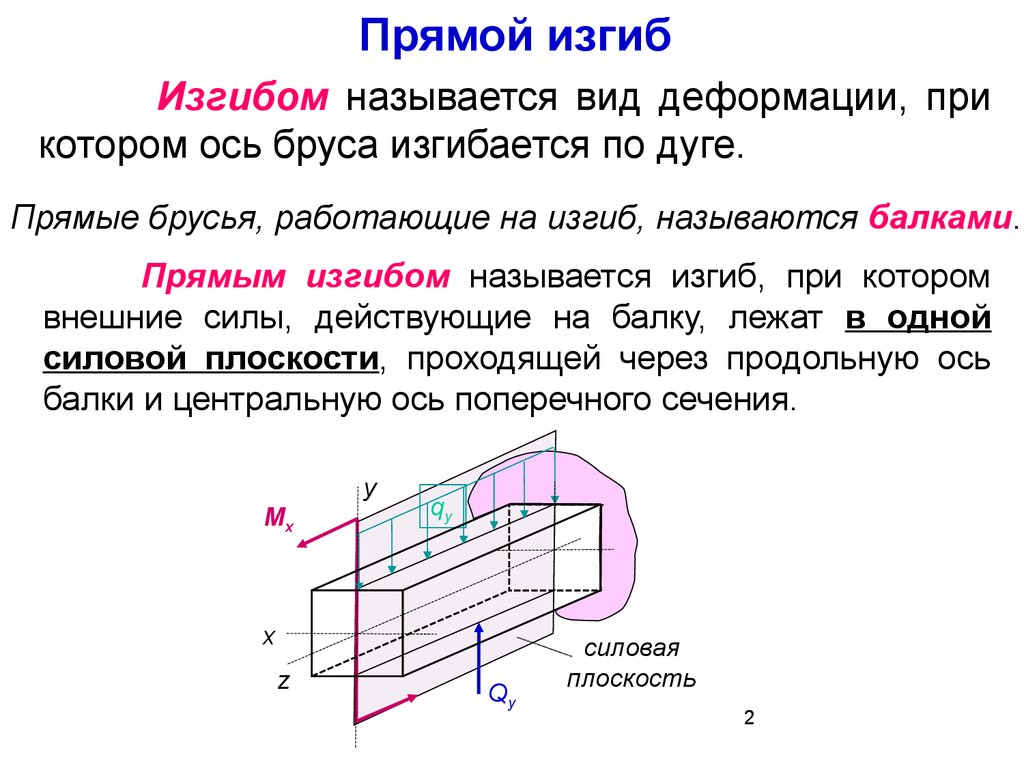
Прямой изгиб
Изгибом называется вид деформации, при
котором ось бруса изгибается по дуге.
Прямые брусья, работающие на изгиб, называются балками.
Прямым изгибом называется изгиб, при котором
внешние силы, действующие на балку, лежат в одной
силовой плоскости, проходящей через продольную ось
балки и центральную ось поперечного сечения.
y
Mx
qy
x
z
Qy
силовая
плоскость
2

3.

Чистый изгиб
Изгиб называется
чистым, если в любом
поперечном сечении балки
возникает
только
один
внутренний
силовой
фактор
изгибающий
момент M x (или M y ).
При этом: Мx(My) = const.
Поперечный изгиб
Изгиб называется
поперечным, если в любом
поперечном сечении балки
возникают два внутренних
силовых
фактора
изгибающий момент M x
и поперечная сила Q y ,
или M y и Qх .
3

4.

Рассмотрим чистый изгиб
По торцам балки приложим два равных и противоположно
направленных изгибающих момента.
Верхние волокна растянуты, а нижние - сжаты. Плоскость, разделяющая
область растяжения от области сжатия, называется нейтральным слоем.
Нейтральной линией называется линия пересечения
нейтрального слоя с плоскостью поперечного сечения балки.
M изг
M изг
z
4

5.

Расчет балки на изгиб основан на справедливости
гипотезы плоских сечений (гипотезы Бернулли).
При чистом изгибе ось бруса изгибается по дуге
окружности, при этом сечения остаются плоскими, но
поворачиваются в пространстве на некоторый угол
друг относительно друга.
Следствие:
В случае чистого изгиба в поперечном сечении бруса
действуют только нормальные напряжения.
5

6.

Нормальные напряжения при чистом изгибе
dN = σdA
N dА 0
d
сила
z
y
А
dM = σdAy
y
M x d А y
dA
y
А
плечо
Mx(z)
Mx(z)
нейтральный
слой
сила
d угол, общей кривизны балки
радиус кривизны нейтрального слоя;
dz d - длина продольных волокон нейтрального слоя.
6

7.

d
z
сила y
z
y
плечо
Mx(z)
нейтральный
слой
Mx(z)
сила
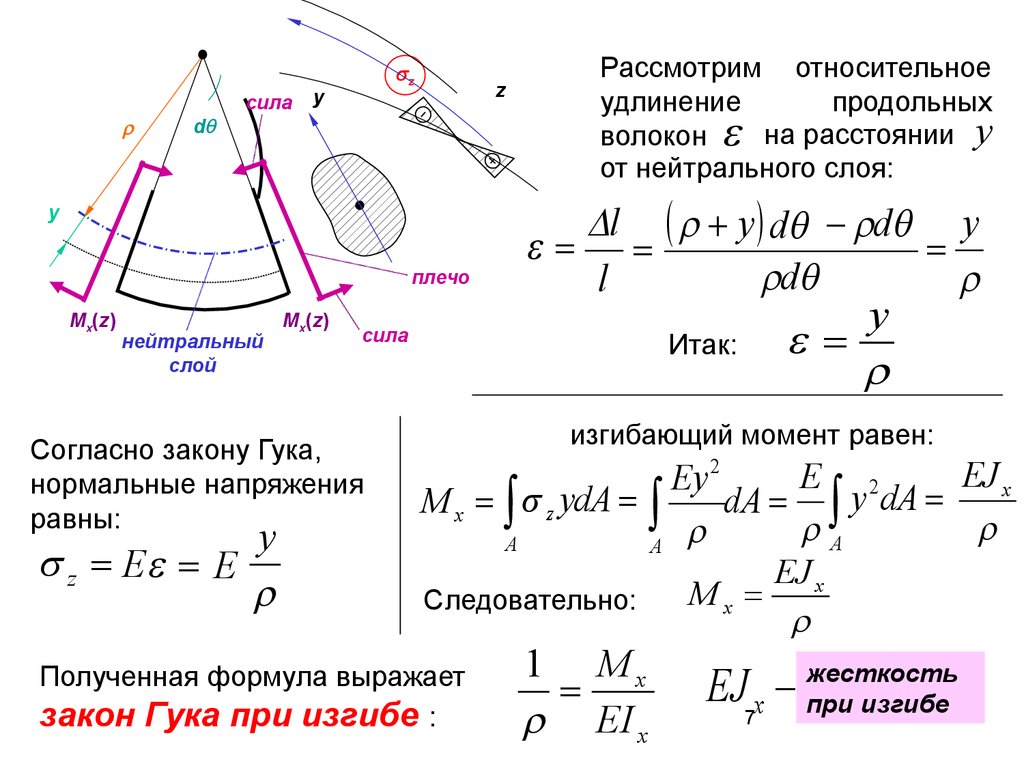
Согласно закону Гука,
нормальные напряжения
равны:
y
z Е E
Рассмотрим относительное
удлинение
продольных
волокон на расстоянии y
от нейтрального слоя:
l y d d y
d
l
y
Итак:
изгибающий момент равен:
EJ x
E 2
Ey 2
M x z ydА
dА y dА
А
А
А
Следовательно:
Полученная формула выражает
закон Гука при изгибе :
1 Мx
ЕI x
EJ x
Mx
EJ7x
жесткость
при изгибе

8.

Mxy
M xE
1
y
,
z Еy
Jx
EJ x
Mxy
z
Jx
Полученная зависимость называется
формулой Навье.
EJ x - Жесткость при изгибе.
Размерность:
Н м
2
Максимальное нормальное напряжение в площади поперечного
сечения балки наблюдается на её поверхности и равно:
z max
Итак, получено:
Mx
Mx
ymax
Wx
Jx
z max
Mx
Wx
Опасным сечением при изгибе называется поперечное сечение
8 напряжение.
бруса, в котором возникает максимальное нормальное

9.

Расчеты на прочность при изгибе
а) проверочный
расчет
Определяется максимальное расчетное напряжение и
сравнивается с допускаемым напряжением.
max
M x max
Wx
Заданы: нагрузка, площадь сечения,
свойства материала.
б) проектировочный
расчет
Производится подбор сечения бруса из условия:
Wx
M x max
Где:
bh 2
Wx
6
Прямоугольное
сечение.
d 3
Wx W y
32
Или:
9
Круглое сечение.

10.

Рациональные типы сечений балок
Спроектировать балку рационального сечения означает
задать ей такие размеры и форму, которые обеспечат при
минимальном расходе материала выполнение условия
прочности.
Несущая способность балки пропорциональна моменту
сопротивления сечения, т.е.
M x Wx
а расход материала – площади поперечного сечения.
Чем меньше площадь поперечного
сечения балки, тем она легче и,
соответственно, экономичнее.
10

11.

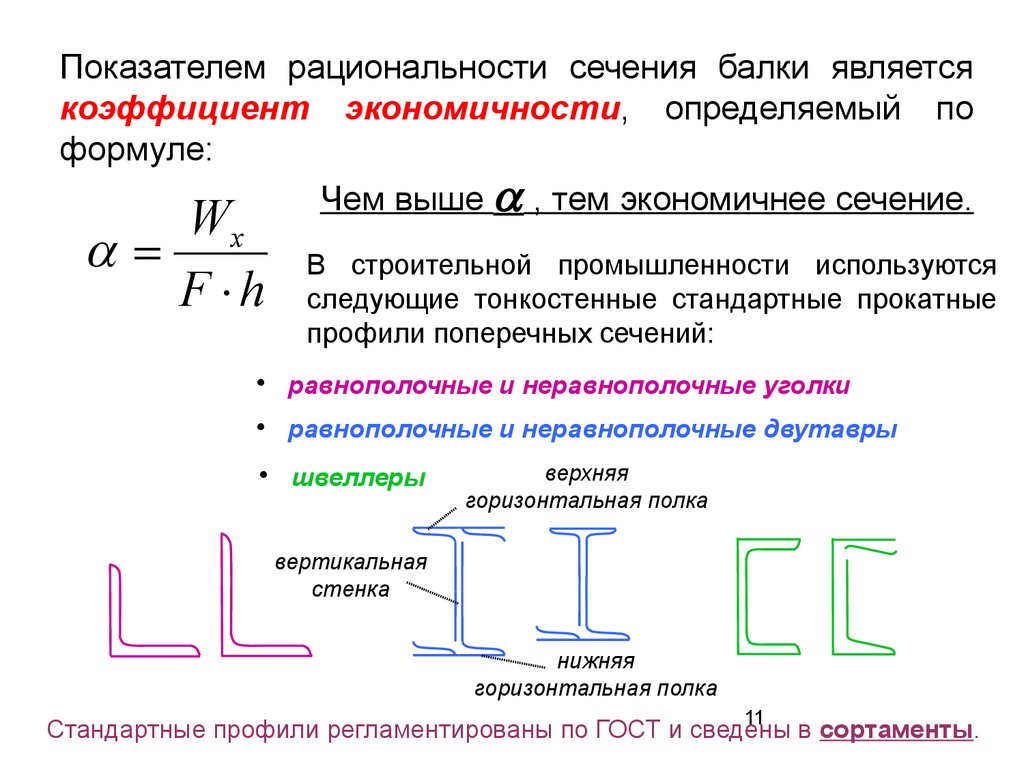
Показателем рациональности сечения балки является
коэффициент экономичности, определяемый по
формуле:
Чем выше , тем экономичнее сечение.
Wx
F h
В строительной промышленности используются
следующие тонкостенные стандартные прокатные
профили поперечных сечений:
• равнополочные и неравнополочные уголки
• равнополочные и неравнополочные двутавры
• швеллеры
верхняя
горизонтальная полка
вертикальная
стенка
нижняя
горизонтальная полка
11
Стандартные профили регламентированы по ГОСТ и сведены в сортаменты.

12.

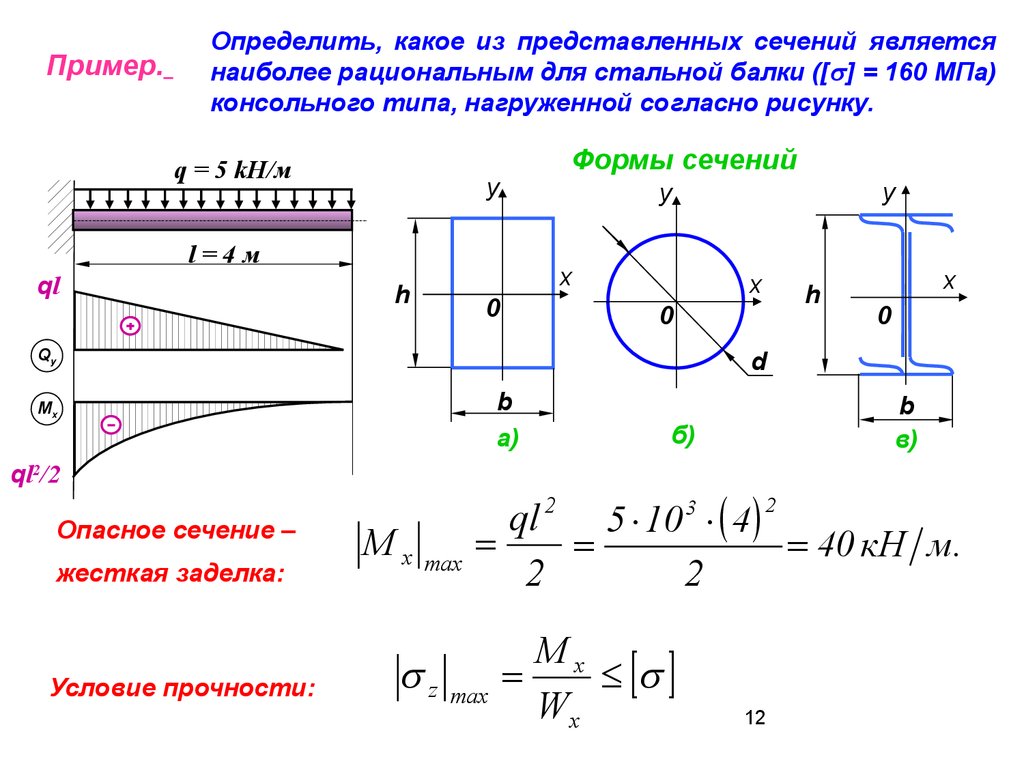
Пример.
Определить, какое из представленных сечений является
наиболее рациональным для стальной балки ([ ] = 160 МПа)
консольного типа, нагруженной согласно рисунку.
q = 5 kH/м
Формы сечений
y
l=4м
ql
x
h
0
x
0
Qy
b
а)
ql2/2
жесткая заделка:
Условие прочности:
h
x
0
d
Mx
Опасное сечение –
y
y
Mx
max
z
b
в)
б)
ql 2 5 10 3 4 2
40 кН м.
2
2
max
Mx
Wx
12

13.

а) прямоугольное сечение
z
max
2
Mx
Wx
2
3
bh
h h
h
Wx
6
2 6 12
h 3
(примем b = h/2)
M x 12
3
h
12 M x 3 12 40 10 3
0 ,144 м 14 ,4 см - требуемая высота сечения.
6
160 10
h
h 2 14,4
A b*h h
1,0368 * 10 2 м 2 103,68см 2 - площадь сечения.
2
2
2
2
h 3 0 ,144
Wx
248 ,33см 3
12
12
3
Wx
248,33
0,166
А h 103,68 14,4
- момент сопротивления сечения.
- коэффициент экономичности сечения.
13

14.

б) круглое сечение
z max
Mx
Wx
d 3
Wx
32
M x 32
3
d
32 M x 3 32 40 10 3
d 3
0 ,136 м 13,6 см
6
3,14 160 10
- требуемый диаметр сечения.
d 2 3,14 0,136
А
1,01452 10 2 м 2 145,2см 2
4
4
2
* d 3 3,14 * 13,6
Wx
246,83см 3
32
32
- площадь сечения.
3
Wx
246,83
0,125
А h 145,2 13,6
- момент сопротивления сечения.
- коэффициент экономичности сечения.
14

15.

в) двутавровое сечение
z
max
Mx
Wx
Mx
40 10 3
3
3
3
Wx
0
,
25
10
м
250
см
160 106
- требуемый момент
сопротивления сечения.
Ближайший момент сопротивления сечения по сортаменту:
что соответствует двутавру № 22 «а».
А 32,8см 2 ,
h 22см.
Wx
254
0,352
À h 32,8 22
Итак, получено:
прямоуг . 0 ,166
кругл . 0 ,125
двут . 0 ,352
Wx 254 см 3 ,
- коэффициент экономичности сечения.
Вывод:
Наиболее
предпочтительным
оказалось двутавровое сечение,
т.к.
его
коэффициент
экономичности максимален.
15

16.

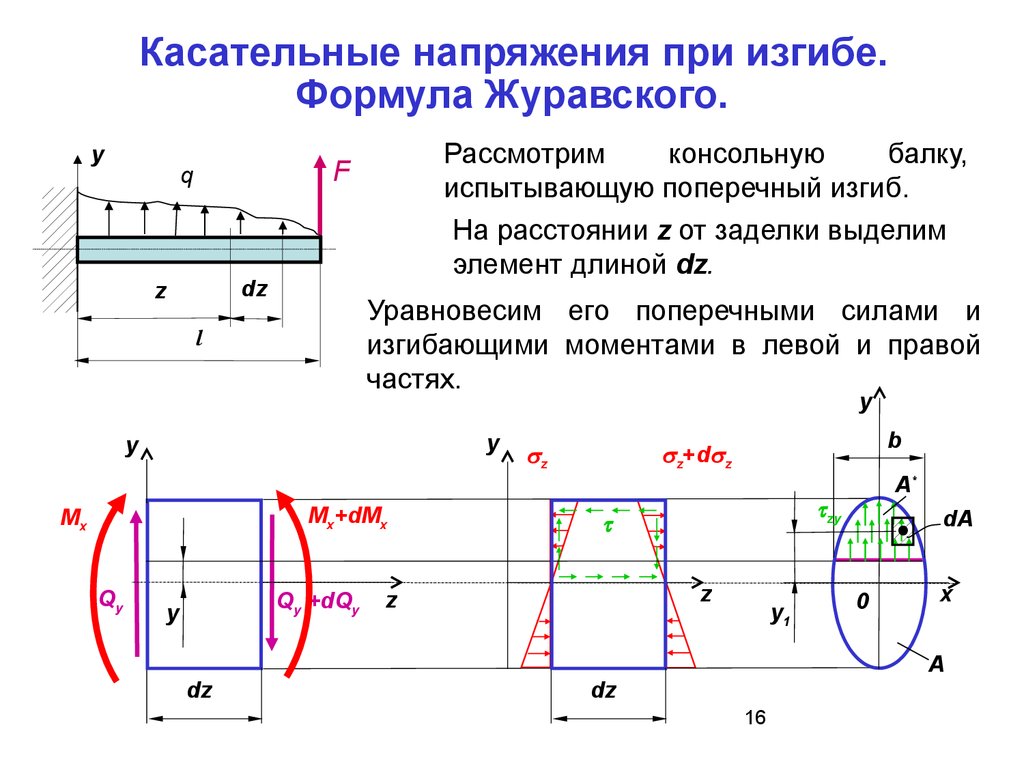
Касательные напряжения при изгибе.
Формула Журавского.
y
Рассмотрим
консольную
балку,
испытывающую поперечный изгиб.
На расстоянии z от заделки выделим
элемент длиной dz.
F
q
dz
z
Уравновесим его поперечными силами и
изгибающими моментами в левой и правой
частях.
l
у
у
у
Mx+dMx
Mx
Qy
Qy +dQy
у
b
z+d z
z
zy
z
z
А*
у1
dА
0
x
А
dz
dz
16

17.

Продольным горизонтальным сечением на расстоянии у от нейтрального слоя
разделим выделенный элемент на две части.
zy
N*+dN*
Рассмотрим равновесие
верхней
части,
имеющей
основание шириной b.
b
z
y
С учетом закона парности
касательных напряжений получаем, что
в поперечном сечении равны
в
продольном сечении, и направлены
перпендикулярно.
zy
yz
x
N*
0
dz
Составим уравнение
F z N N
F z 0
i
dN yzb dz 0
dN
(1)
dN yz bdz откуда: yz
bdz
M
M
M
N dА x y1 dА x y1dА x S x т.е. N M x S тогда:
x
Jx
Jx А
A Jx
J
А
i
dM x
dN
Sx
Jx
(2)
Подставим (2) в (1) :
x
yz
dM x S x Q y S x
J x bdz
J xb
17

18.

Полученная зависимость называется
формулой Журавского :
где:
yz
Qy поперечная сила, (Н);
S x
Q y S x
J xb
статический момент отсеченной части сечения,
находящейся выше (или ниже) некоторой
характерной точки, (м3);
Характерными будем считать точки на оси ординат, располагающиеся по верхней и
нижней образующей сечения, в местах изменения его ширины, а также в центре
тяжести сечения.
где:
А
y
x
S А y
– площадь части сечения выше (ниже) характерной точки, (м2);
– расстояние от центра тяжести площади
до центра тяжести сечения, (м);
A
b – ширина сечения в некоторой характерной точке, (м);
J x – момент инерции всего сечения относительно
центральной оси х (м4).
18

19.

Получим формулу для определения статического момента
прямоугольного сечения со сторонами b и h в общем случае, при:
h
0 y
2
y
А*
C*
y*
h
x
у
0
b
h
y
h 2
*
y
Sx А y b y
2
2
h
h y
b y y
2
4 2
h 2 hy hy y 2
h2 y 2
h
h y
b y b b
2
4 2
8 4 4 2
8 2
b h2
2
2
b h
y
2
Итак, получено:
S x y
2 4
2 194

20.

Пример.
Определить касательные напряжения по высоте прямоугольного (а) и круглого (б)
сечения консольной балки, нагруженной положительной силой F на свободном
правом торце, построить эпюру .
yz
1 0
Qy S x
J xb
S x 0
т.к.
S x А y
(А*=0)
У*=h/4 – коордоната
ц.т.сечения выше оси х
а)
h
x
h/4
0 (3)
b (2)
3
y (1)
1
2 0
max
т.к.
S x 0
(А*=0)
h h
Qy b
3Q y
2
4
max
bh 3
2bh
b
12
т.к.
h h bh 2
S А y b
Sx
2 4
8
x
*
20
max

21.

б)
брус круглого сечения
1
у
А*
R
С
у*
3
О
2
т.к.
S x 0
2 0
т.к.
S x 0
Выше точки 1 и ниже точки 3
площадей нет
max
x
1 0
3
2R3
Q y 3
R
2R
4
4
4Q y
3 R
2
max
Определим статический момент площади, находящейся выше точки 3:
R2 4R 2 3
S А y
R Sx
2 3 3
x
*
подставим
max
S xmax в 3
Площадь эпюры касательных напряжений (также как и для
прямоугольного сечения) ограничивается параболой второй
степени.
Направление действия напряжений
действия поперечной силы.
совпадает
с
21
направлением

22.

зависимость от у в сечении определяется
S
через статическийследовательно,
момент x
независимо от формы поперечного сечения,
max достигается в центре его тяжести, т.к. в нем
S x max т.к. А max .
0 в верхней и нижней точках по высоте сечения,
т.к. в них S x 0 т.к. А 0
выше и ниже характерных точек по верхней и
нижней образующим сечения.
Вывод:
Касательные напряжения, возникающие в брусе
при поперечном изгибе, обычно на порядок меньше
нормальных напряжений, поэтому в упрощенных
расчетах стальных балок на прочность ими
пренебрегают.
22

23.

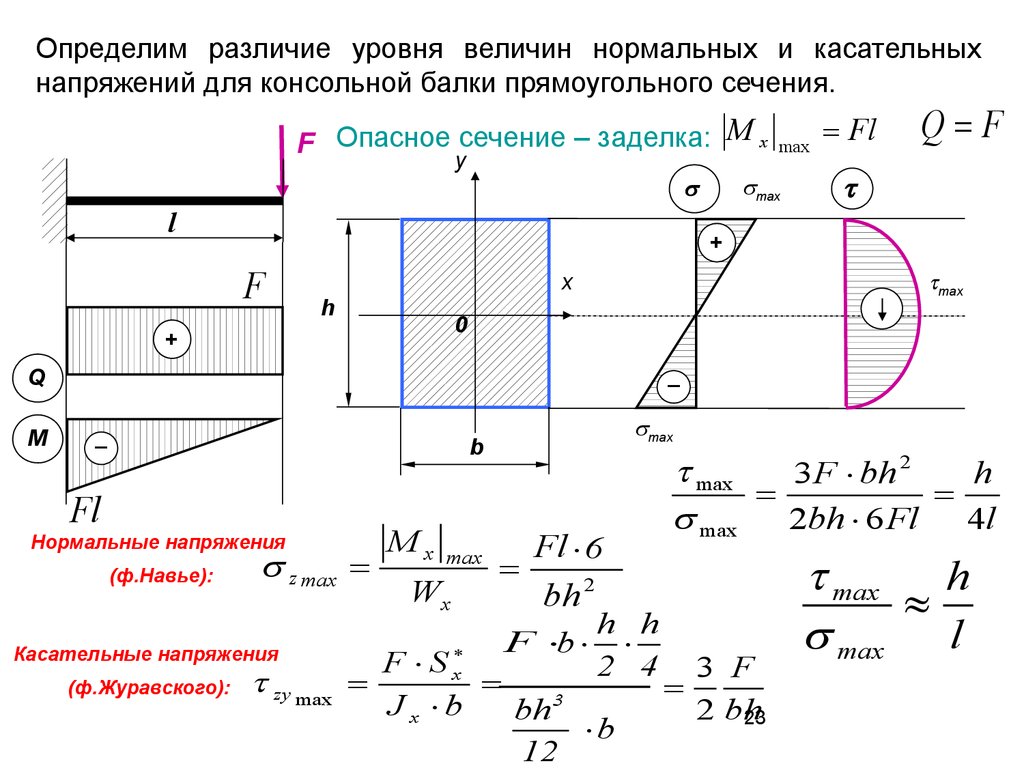
Определим различие уровня величин нормальных и касательных
напряжений для консольной балки прямоугольного сечения.
F Опасное сечение – заделка: M x
y
Fl
Q F
+
F
max
x
h
0
+
_
Q
M
max
l
max
_
max
b
Fl
Нормальные напряжения
(ф.Навье):
z max
Касательные напряжения
(ф.Журавского):
zy max
Mx
max
Wx
Fl 6
bh 2
F b
h h
2 4
F S x
Jx b
bh 3
b
12
max
3F bh 2
h
max
2bh 6 Fl 4l
3 F
2 bh
23
max
h
max
l