Похожие презентации:
Кинематический анализ механизмов
1.
Лекция 2Кинематический
анализ
механизмов
1
Лекция 2 - Кинематический анализ механизмов
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ
Лекция 2КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ
Кинематический
анализ
механизма
—
определение движения звеньев механизма по
заданному движению начальных звеньев. При этом
размеры звеньев механизма заданы.
К кинематическим параметрам механизмов
относятся:
1) перемещения (угловые и линейные) звеньев,
траектории точек звеньев, положения звеньев;
2) скорости (угловые и линейные) звеньев и точек
звеньев;
3) ускорения (угловые и линейные) звеньев и
точек звеньев.
2
Лекция 2 - Кинематический анализ механизмов
3. Методы кинематического анализа
Лекция 2Методы кинематического анализа
графоаналитические (метод планов
скоростей и ускорений, численные методы с
применением ЭВМ);
аналитические (методы с
использованием замкнутых векторных
контуров).
графические (метод кинематических
диаграмм, метод обращения движения).
3
Лекция 2 - Кинематический анализ механизмов
4. Кинематика входных звеньев
Схемы входных звеньев механизмов4
Лекция 2 - Кинематический анализ механизмов
Лекция 2
5. Кинематика входных звеньев
Лекция 2Если законы движения входных звеньев заданы
в аналитической форме или графически в виде
функций f (t ) или S f (t ) , то скорости и
ускорения входных звеньев определяются как:
d
d 2
dS
d 2S
; 2 ;
V ;a 2 ;
dt
dt
dt
dt
аналитическими или графическими методами.
Если законы движения входных звеньев заданы в
виде функций f (t ); f (t ) или V f (t ); a f (t ) , то
функции перемещения определяются их
интегрированием.
5
Лекция 2 - Кинематический анализ механизмов
6. Кинематика входных звеньев
Лекция 2При вращательном движении входного звена скорость любой
его точки А направлена перпендикулярно к звену в сторону
вращения и равна по модулю
VA lOA .
(1)
n
t
Ускорение т.А равно: a A a A a.A .
(2)
Модуль нормальной составляющей ускорения
2
n
2
V
или
(3)
n
A .
a A lOA
aA
lOA
Модуль тангенциальной составляющей ускорения
atA
lOA .
При поступательном движении входного звена скорость и
ускорение любой его точки параллельны направляющей.
6
Лекция 2 - Кинематический анализ механизмов
(4)
7. АНАЛОГИ СКОРОСТЕЙ И УСКОРЕНИЙ
Лекция 2При кинематическом анализе механизмов скорости и
ускорения ведомых звеньев и точек, им принадлежащих,
удобно выражать в виде функций:
d i d i d
d i
(5)
i
i ,
dt
d dt
d
dri dri d
dri
Vi
S i ,
dt d dt
d
где
i - безразмерная угловая скорость звена i ,
называемая аналогом угловой звена i ;
S i - аналог скорости точки звена i , имеющий
размерность длины.
7
Лекция 2 - Кинематический анализ механизмов
(6)
8. АНАЛОГИ СКОРОСТЕЙ И УСКОРЕНИЙ
iЛекция 2
d i d
d i
d
i
i
i
dt dt
dt
dt
d i d
i 2 i i ,
d dt
dVi d
ai
S i 2 S i S i ,
dt dt
- аналог углового ускорения звена i ;
S i - аналог ускорения точки звена i .
Аналоги угловых скоростей по своему физическому
смыслу есть передаточные отношения:
где
i
i.
8
Лекция 2 - Кинематический анализ механизмов
(7)
(8)
9. АНАЛОГИ СКОРОСТЕЙ И УСКОРЕНИЙ
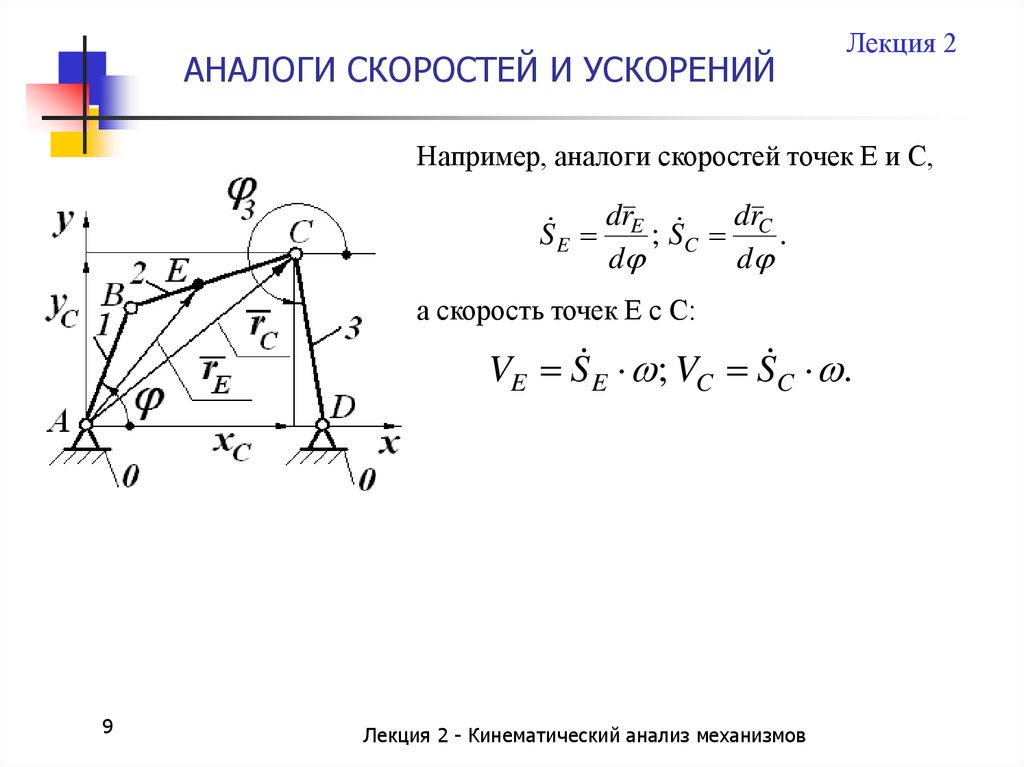
Лекция 2Например, аналоги скоростей точек Е и С,
drE
drC
SE
; SC
.
d
d
а скорость точек Е с С:
VE S E ; VC S C .
9
Лекция 2 - Кинематический анализ механизмов
10. Сложное движение точки или тела
Лекция 2Сложное движение точки или тела
При сложном движении точки или тела движение
рассматривается одновременно в основной и подвижной
системах отсчета.
Движение точки или тела по отношению к основной
системе отсчета называется абсолютным движением.
Движение точки или тела по отношению к подвижной
системе отсчета называется относительным
движением.
Движение подвижной системы отсчета по отношению
к основной системе отсчета называется переносным
движением.
10
Лекция 2 - Кинематический анализ механизмов
11. Сложное движение точки или тела
Лекция 2Сложное движение точки или тела
Элементы абсолютного движения обозначаются индексом а , относительного – r, переносного – е.
Теорема сложения скоростей при сложном движении
точки гласит:
(9)
V a V e V r .
При определении переносной скорости V e точки предполагается, что относительное движение точки остановлено.
При плоском движении звена переносное движение
является поступательным со скоростью произвольно выбранной точки звена, принятой за полюс, а относительное
движение является вращательным вокруг этой точки.
Угол и направление поворота от выбора полюса не зависят.
11
Лекция 2 - Кинематический анализ механизмов
12. Сложное движение точки или тела
Лекция 2Сложное движение точки или тела
Абсолютное ускорение а а любой точки звена при
плоскопараллельном движении:
a a ae a r
n
ae a r
t
ar ,
(10)
В случае, когда переносное движение при сложном
движении точки не является поступательным, то абсолютное ускорение точки равно векторной сумме трех ускорений: переносного, относительного и Кориолисова:
a a a e a r ак
12
n
ae a r
2( V r ).
Лекция 2 - Кинематический анализ механизмов
(11)
13. Сложное движение точки или тела
Лекция 2Сложное движение точки или тела
Если рассматривается совокупность элементов,
то эти индексы опускают и вводят в качестве подстрочного индекса обозначение точки и номер звена,
например, V B2 , V C3 , V C3B2 . Если принадлежность точек
к звену оговорена отдельно или ясно видна по кинематической схеме, то номер звена можно опускать,
например, V B , V C , V CB . Векторные уравнения (1) и (2)
применяют для построения планов скоростей и ускорений точек звеньев механизмов.
13
Лекция 2 - Кинематический анализ механизмов
14. Графические методы
Лекция 2Изображение кинематической схемы механизма в
выбранном масштабе l , соответствующее
определенному положению начального звена (или
начальных звеньев), называется планом механизма .
Планы механизма, построенные за цикл движения,
называются совмещенными.
Планы механизма определяют положения, законы
перемещения звеньев, например,
S f ( ), f ( ).
14
Лекция 2 - Кинематический анализ механизмов
15. План шестизвенного механизма
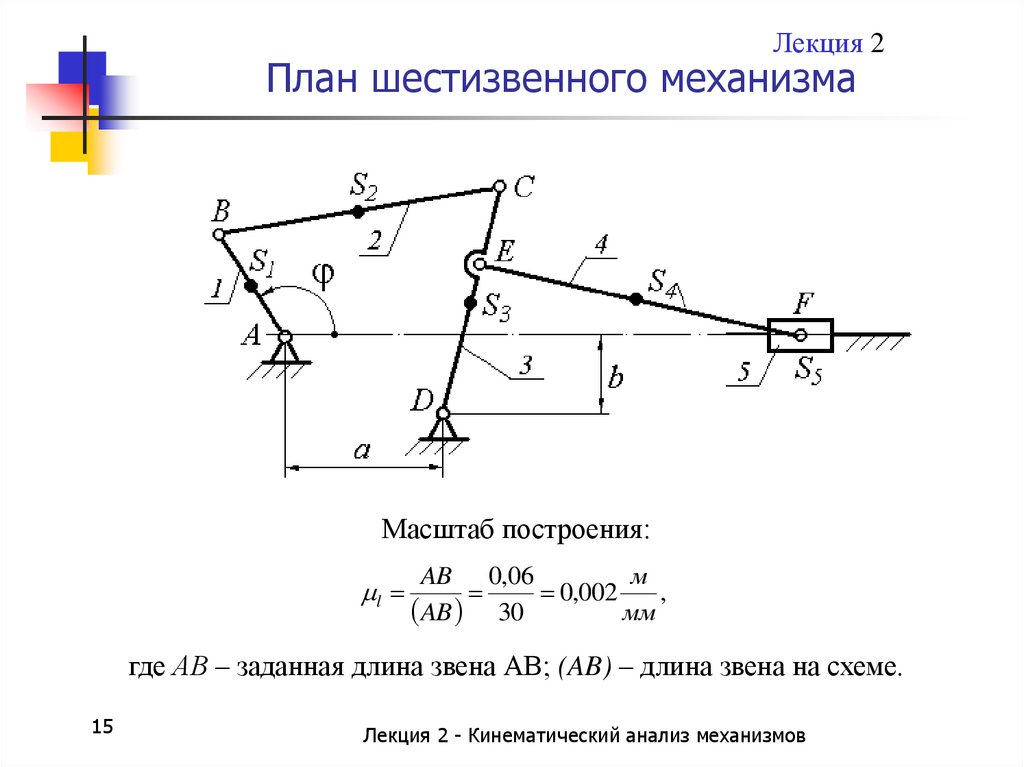
Лекция 2План шестизвенного механизма
Масштаб построения:
l
AB 0,06
м
0,002
,
AB 30
мм
где АВ – заданная длина звена АВ; (AB) – длина звена на схеме.
15
Лекция 2 - Кинематический анализ механизмов
16. Совмещенные планы механизма
SПо перемещениям
зависимости
16
Лекция 2
F
S
точки
F
ползуна строится график
S f ( ).
Лекция 2 - Кинематический анализ механизмов
17. Построение графика перемещения ползуна
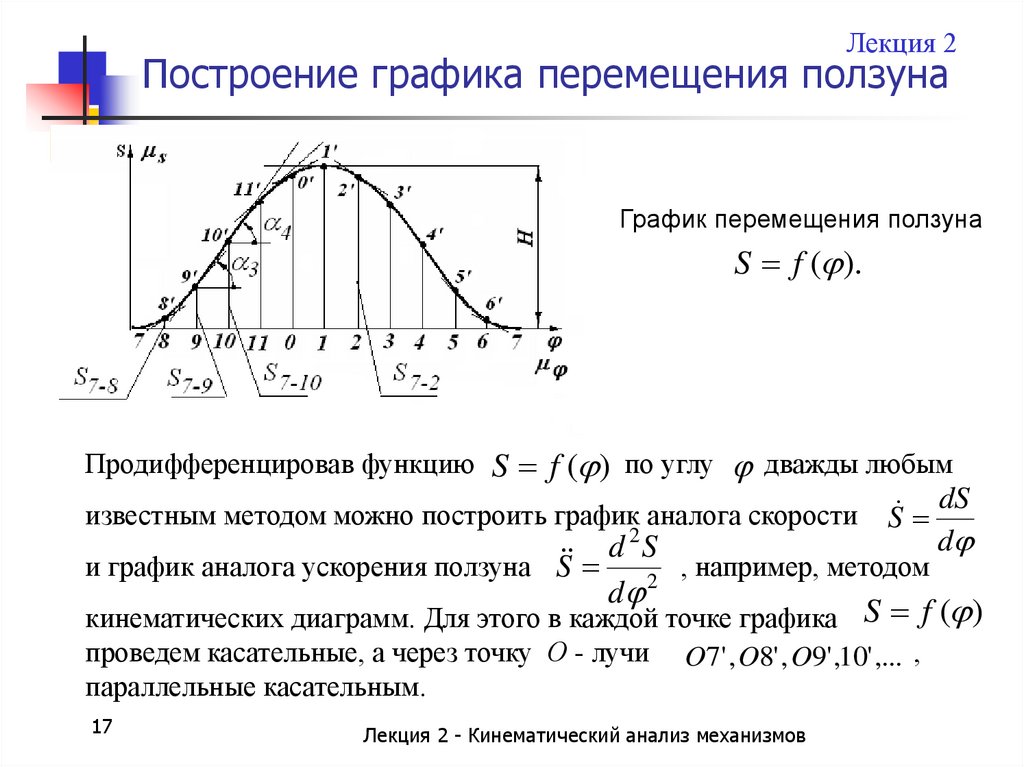
Лекция 2Построение графика перемещения ползуна
График перемещения ползуна
S f ( ).
Продифференцировав функцию S f ( ) по углу
дважды любым
известным методом можно построить график аналога скорости
dS
S
d
2
d
S
и график аналога ускорения ползуна S
, например, методом
2
d
кинематических диаграмм. Для этого в каждой точке графика S f ( )
проведем касательные, а через точку О - лучи
параллельные касательным.
17
O7' , O8' , O9' ,10' ,... ,
Лекция 2 - Кинематический анализ механизмов
18. Построение графика перемещения ползуна
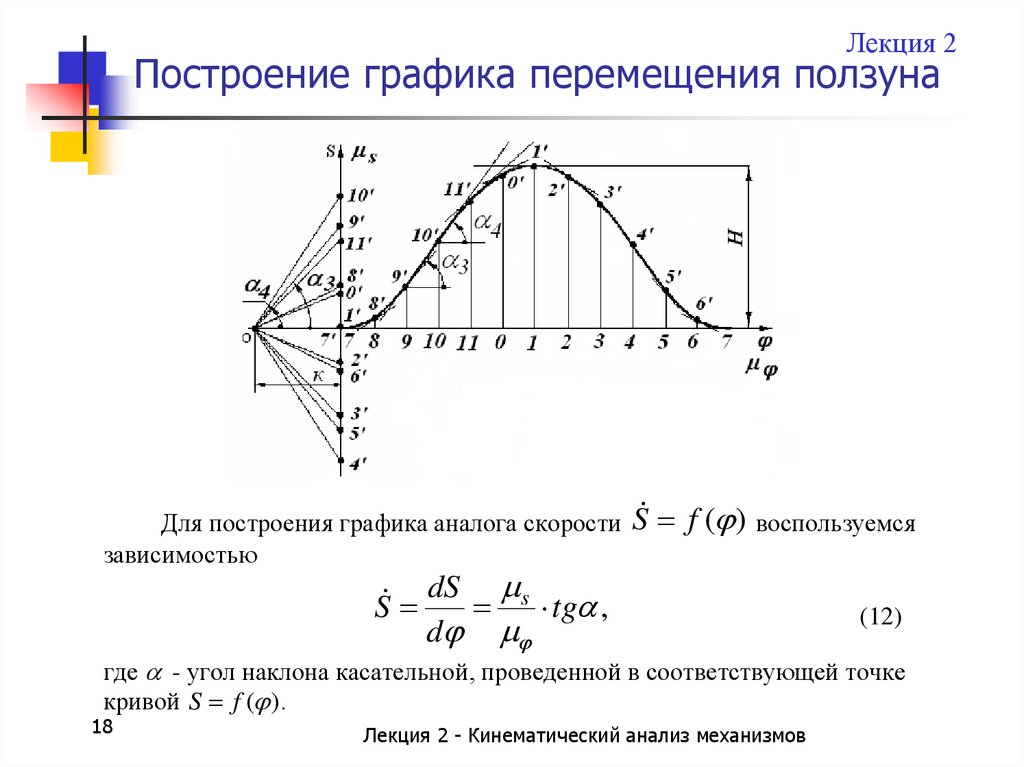
Лекция 2Построение графика перемещения ползуна
Для построения графика аналога скорости
зависимостью
S f ( ) воспользуемся
dS s
S
tg ,
d
(12)
где - угол наклона касательной, проведенной в соответствующей точке
кривой S f ( ) .
18
Лекция 2 - Кинематический анализ механизмов
19. Построение графика перемещения ползуна
Лекция 2Построение графика перемещения ползуна
Помножим и разделим выражение (12) на величину, равную к (расстояние от
начала координат до точки О называется коэффициентом дифференцирования)
в мм:
s
S
k tg .
k
(13)
Но величина k tg для касательных, проведенных в различных точках,
равняется отрезкам (7' 8' , 7' 9' ,7' 10' ,...) . Следовательно, аналоги скорости
пропорциональны отрезкам
рости:
Si , измеренным в мм. Масштаб s аналогов ско-
S м рад 1
S
k мм .
Отрезки (7' 8' , 7' 9' ,7' 10' ,...) откладываются на соответствующих ординатах
графика
S f ( ) .
Аналогично строится график зависимости
19
S i
S f ( ) аналогов ускорения.
Лекция 2 - Кинематический анализ механизмов
(14)
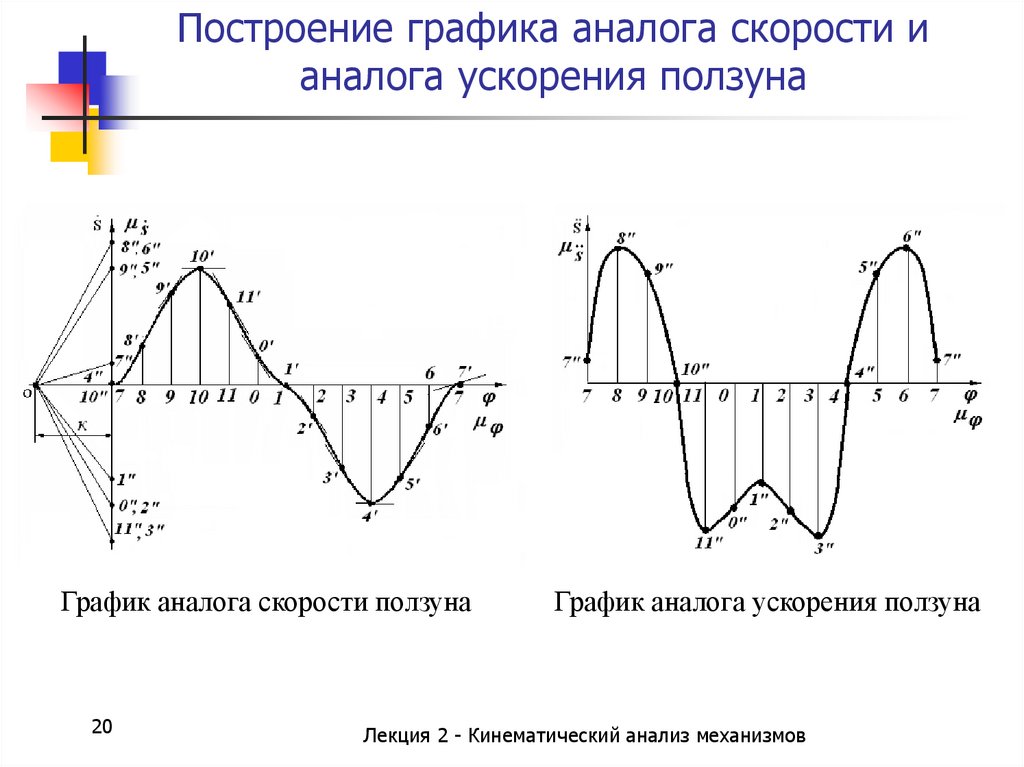
20. Построение графика аналога скорости и аналога ускорения ползуна
График аналога скорости ползуна20
График аналога ускорения ползуна
Лекция 2 - Кинематический анализ механизмов
21. Графоаналитические методы
Лекция 2Графоаналитические методы
Планом скоростей (ускорений) механизма называется чертеж, на
котором изображены в виде отрезков векторы, равные по модулю и по
направлению скоростям (ускорениям) различных точек механизма в данный
момент.
Сформулируем свойства планов скоростей и ускорений:
1) векторы абсолютных скоростей (ускорений) направлены из полюса;
2) векторы, соединяющие концы векторов абсолютных скоростей
(ускорений), есть векторы относительных скоростей (ускорений);
3) точки, у которых скорости (ускорения) равны нулю, расположены в
полюсе;
4) векторы относительных скоростей (полных относительных
ускорений) образуют на плане скоростей (ускорений) фигуру, подобную
жесткому контуру на плане механизма;
5) планы скоростей и ускорений позволяют определять величину и
направление угловых скоростей и ускорений.
21
Лекция 2 - Кинематический анализ механизмов
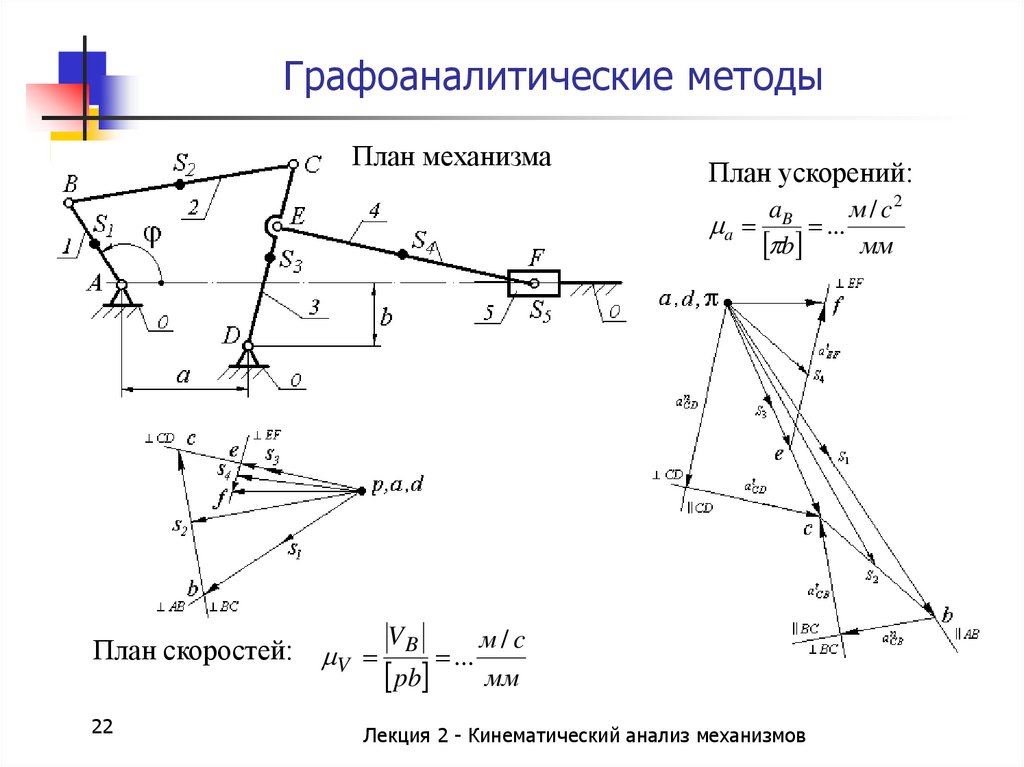
22. Графоаналитические методы
.План механизма
План ускорений:
aB
м / c2
a
...
b
мм
План скоростей: V
22
VB
pb
...
м/c
мм
Лекция 2 - Кинематический анализ механизмов
23. Графоаналитические методы
Лекция 2Модуль скорости точки В определяется по формуле:
VB AB.
(15)
Масштаб плана скоростей определяется как
VB
м/c
V
...
.
pb
мм
(16)
В плоскопараллельном движении скорость точки С определяется
из системы уравнений:
V C V B V CB ;
V C V D V CD .
23
Лекция 2 - Кинематический анализ механизмов
(17)
24. Графоаналитические методы
Лекция 2Через точку b плана скоростей проводим прямую
перпендикулярно звену ВС, а через полюс p проводим прямую перпендикулярно звену CD. Точка c пересечения этих прямых будет являться вектором абсолютной скорости точки С, а отрезок pc в масштабе
V будет являться вектором скорости V C . Отрезок bc
будет являться вектором относительной скорости
V CB .Модули скоростей V C и V CB определятся как
VC pc V ; VCB bc V .
24
Лекция 2 - Кинематический анализ механизмов
25. Графоаналитические методы
Лекция 2Скорость точки Е определяется на основании
свойств подобия, для чего отрезок pc cd на плане скоростей разбивается пропорционально отрезкам СЕ и ЕD
на плане механизма:
pc ep , откуда ep pc ED .
CD
ED
CD
Скорость точки F определяется из следующего уравнения:
V F// V E V FE .
(18)
Ускорение точки В определится из следующего уравнения:
n
t
a B a A a BA a BA .
(19)
n
aBA
2 AB; a BA AB.
t
25
Лекция 2 - Кинематический анализ механизмов
26. Графоаналитические методы
Лекция 2Если ведущее звено АВ вращается с постоянной угловой скоростью , тогда его угловое ускорение 0 .
Масштаб плана ускорения определяется как
aB
м / c2
a
...
.
b
мм
В плоскопараллельном движении ускорение точки С
определяется из системы уравнений:
n
t
aC a B aCB
a
CB ;
//
n
t
aC a D aCD // aCD .
(20)
n
a CB
n
a CD
Нормальные ускорения точки С
и
направлены из точки С параллельно звеньям ВС и СD, а тангенt
t
циальные ускорения a CB и a CD - перпендикулярно
звеньям
ВС и СD.
26
Лекция 2 - Кинематический анализ механизмов
27. Графоаналитические методы
Лекция 2Графоаналитические методы
Модули нормальных ускорений точки С определяются
по формулам:
2
bc V ;
VCB
BC
BC
2
n
aCB
VC2 pc V
.
CD
CD
2
n
aCD
Ускорение точки Е определяется также на основании
свойств подобия отрезков на плане ускорений и жестких
c e
контуров на кинематической схеме механизма: CD ED .
Ускорение точки F определяется из следующего уравнения:
n
t
a F// a E a FЕ// a FE .
27
Лекция 2 - Кинематический анализ механизмов
(21)
28. Графоаналитические методы
Лекция 2n
a FE
Нормальное ускорение
направлено из точки F
n
параллельно звену EF. Модуль вектора a FE определяется по формуле
2
2
V
(
fe
)
n
V
aFE
FE
.
FE
FE
По планам скоростей и ускорений определяются
также угловые скорости и угловые ускорения звеньев,
например:
VCB
2
;
BC
28
t
aCB
2
.
BC
Лекция 2 - Кинематический анализ механизмов
29. Аналитические методы
Лекция 2Аналитические методы основаны на том, что
кинематическую схему механизма представляют в виде
векторных многоугольников, простейшими из которых
являются треугольники и четырехугольники. Проецируя
векторные многоугольники на оси прямоугольной системы
координат, получаем систему уравнений, из которой
определяются координаты (линейные и угловые). Затем
дифференцированием полученных уравнений по
обобщенным координатам определяются аналоги
скоростей и ускорений.
29
Лекция 2 - Кинематический анализ механизмов
30. Аналитические методы
Лекция 2Если каждое звено механизма представить как вектор, то для
простейших механизмов можно записать:
l1 l2 l0 l3.
Из условия замкнутости векторных многоугольников для схем а)
и б):
l1 cos 1 l 2 cos 2 l 0 l3 cos 3 ;
l1 sin 1 l 2 sin 2 l3 sin 3 .
30
Лекция 2 - Кинематический анализ механизмов
31. Аналитические методы
Лекция 2l1 cos 1 l 2 cos 2 l3 ;
l1 sin 1 l 2 sin 2 l 0 .
Определение скоростей и ускорений сводится к
дифференцированию по времени составленных уравнений, например, для схемы б):
1 l1 sin 1 2 l 2 sin 2 VC ;
1 l1 cos 1 2 l 2 cos 2 0.
31
Лекция 2 - Кинематический анализ механизмов

























 Механика
Механика








