Кинематическое исследование механизмов

1.

Кинематическое исследование
механизмов
Задачи :
1.
Определение положений механизма и
траектории движения его отдельных точек;
Определение линейных скоростей и ускорений
точек и угловых скоростей и ускорений звеньев.
2.
Методы:
1.
2.
3.
Аналитический
Графо-аналитический (метод планов)
Графический (метод кинематических диаграмм)

2.

Метод планов
Сущность метода (основная идея):
Графическое решение системы векторных уравнений.
Реализация:
1.
2.
Последовательно по группам Ассура, начиная с
начального механизма
Построить план положений механизма.
Построить планы скоростей.
3.
Построить планы ускорений.

3.

Масштаб и масштабный коэффициент
Масштабным коэффициентом физической величины
называют отношение численного значения физической
величины к длине отрезка в миллиметрах,
изображающего эту величину
Пусть какая либо величина А (например, длина, скорость,
сила и т.п.) изображается на чертеже отрезком, имеющим
длину а. Тогда масштабный коэффициент, с помощью
которого эта величина изображена на чертеже, будет
A
a

4. Примеры

Масштаб и масштабный коэффициент
Примеры
Звено, имеющее длину 0,5 м, изображено на
чертеже 50 мм. Определить масштаб длин μS.
0,5
м
S
0,01
50
мм
Скорость vA=80 м/с некоторой точки А изображена на
чертеже отрезком, имеющим длину 16 мм. В каком
масштабе μv изображена скорость?
80
м/c
V 5
16
мм

5. Построение механизма в масштабе

План положений
Построение механизма в масштабе
Схема механизма вычерчивается в масштабе по ГОСТ 2.302-68 и
Ст. СЭВ 1180-78.
Задается масштабный коэффициент:
μL=….. мм/мм
(….миллиметров объекта в миллиметре чертежа)
Уменьшающие коэффициенты:
1; 2; 2,5; 4; 5; 10…
Увеличивающие коэффициенты: 0,1; 0,2; 0,25; 0,5; ..
0,01; 0,02; 0,025…

6.

План положений
Находятся размеры звеньев на чертеже:
AB
l AB
L
... мм; BC
lBC
L
... мм; CD
lCD
L
... мм; ....
Строится рабочее положение механизма.
(Обратить внимание: на рабочем положении буквы пишутся
заглавными буквами)

7.

План положений
Построение механизма методом засечек
E
C
B
А
D

8.

Планы скоростей и ускорений
Планом
скоростей
(ускорений)
называется
диаграмма, на которой от некоторого центра (полюса)
отложены векторы скоростей (ускорений) точек тела
VB VA VBA
VBA
А
VA
В
VB
VA
V BA

9.

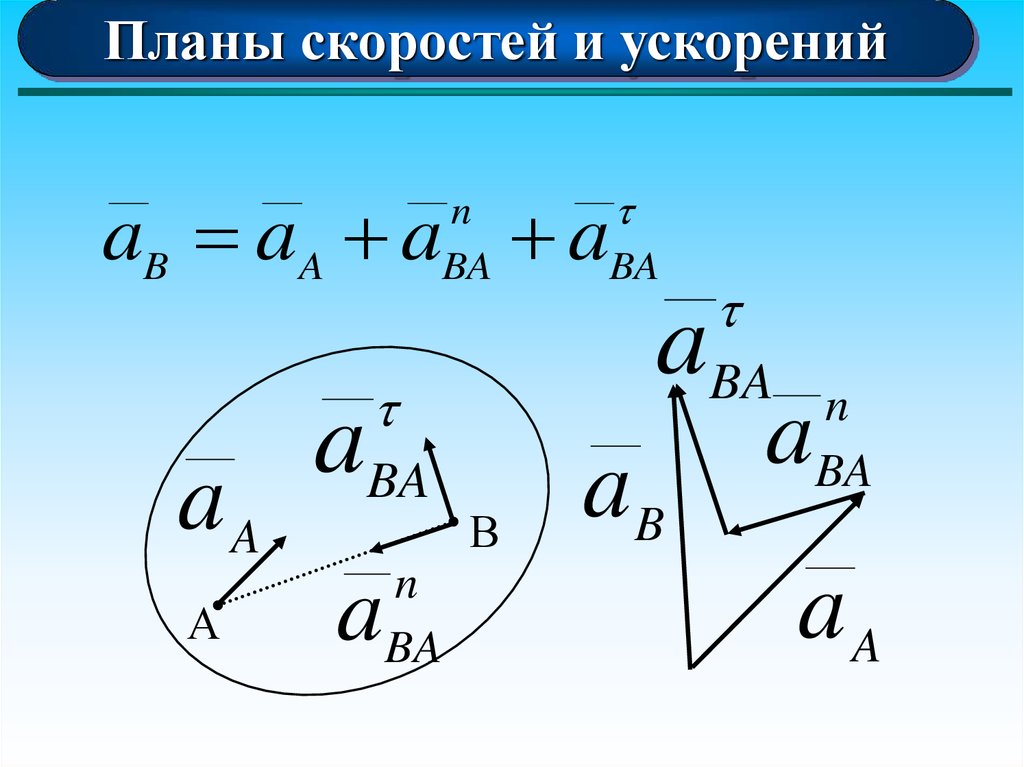
Планы скоростей и ускорений
aB aA a aBA
n
BA
aA
А
a
n
BA
aBA
aBA
В
aB
a
n
BA
aA

10.

Планы скоростей и ускорений
Свойства планов скоростей и ускорений
1. Векторы выходящие из полюса плана скоростей
(ускорений) изображают в масштабе векторы
абсолютных скоростей (ускорений) соответствующих
точек
2. Отрезки, соединяющие концы векторов, выходящих
из полюса, изображают в масштабе векторы
относительных
скоростей
(ускорений)
соответствующих точек
3. Сходственные фигуры звеньев на плане механизма и
плане скоростей (ускорений) – подобны
Примечание (правило обхода букв): направление обхода
букв сходственных фигур на плане механизма и плане
скоростей (ускорений)- одинаково

11.

Планы скоростей и ускорений
Определить
B
1
А
1
VВ ,VС ,VE ,
2
aB , aC , aE ,
D
E
3
C
2 , 3
2 , 3

12.

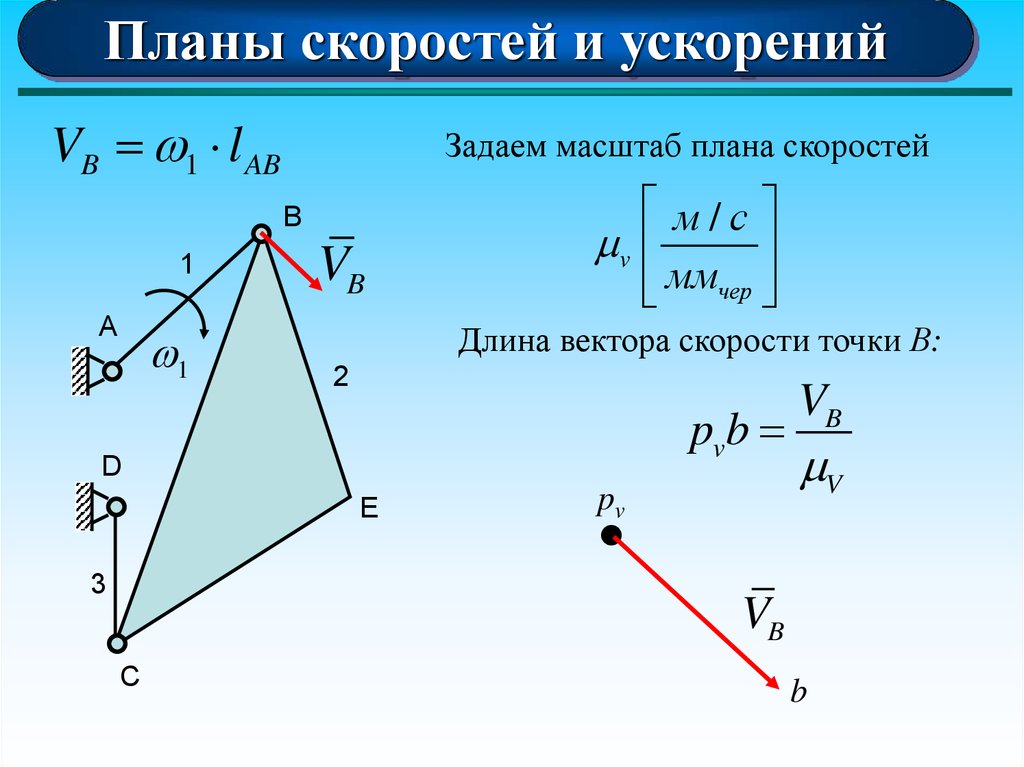
Планы скоростей и ускорений
VB 1 l AB
Задаем масштаб плана скоростей
B
1
А
1
VB
м/c
v
ммчер
Длина вектора скорости точки В:
2
pvb
D
E
3
pv
VB
V
VB
C
b

13.

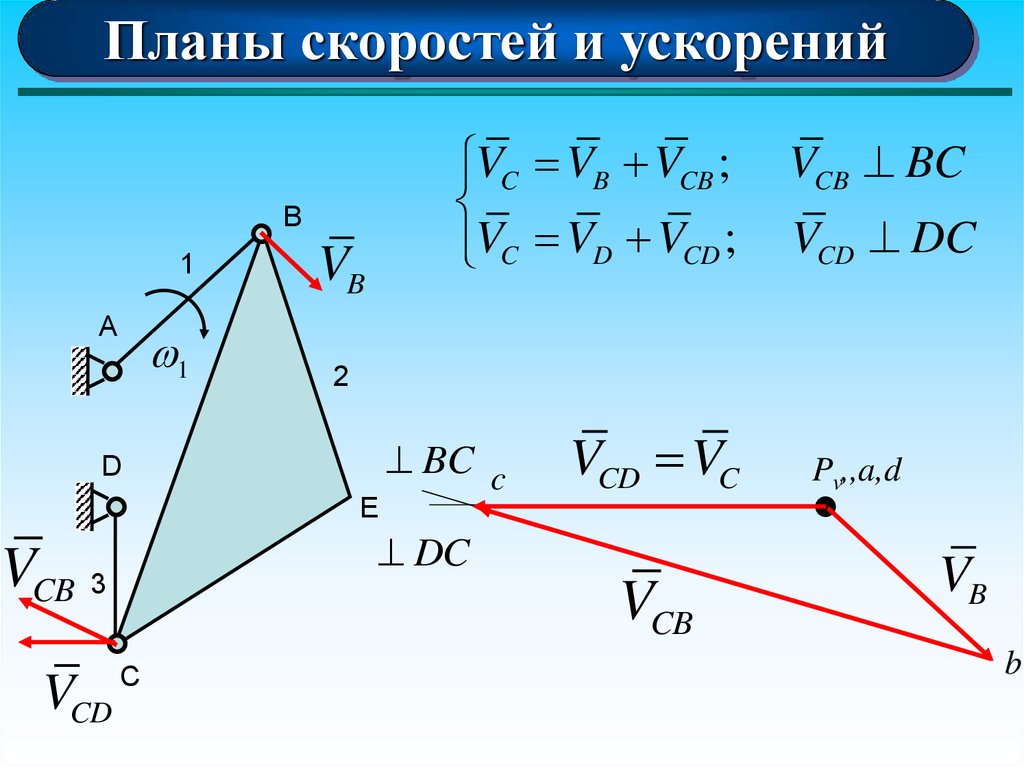
Планы скоростей и ускорений
VC VB VCB ;
VC VD VCD ;
B
1
А
1
VB
VCB BC
VCD DC
2
BC c
D
VCD VC
Pv,,a,d
E
DC
VCB 3
VCD
VCB
C
VB
b

14.

Планы скоростей и ускорений
BC c
B
VB
1
А
1
D
VCB
3
VCD
C
pv
DC
VCB
VB
b
2
2
VCD VC
Из плана находим
E
VC pv c v
VCB bc v
2
lCB
lCB
VCD dc v
3
lCD
lCD

15.

Планы скоростей и ускорений
Скорость точки Е найдем по правилу подобия
BCE
B
1
А
1
2
BC c
E
VCB 3
VCD
BE be
BC bc
CE ce
BC bc
VB
D
bce
bc BE
be
BC
bc CE
ce
BC
VCD VC
DC
VCB
C
VE pv e v
VE
e
pv
VB
b

16.

Планы скоростей и ускорений
aB aBn 12 l AB
aB
Задаем масштаб плана ускорений
м / c2
a
ммчер
B
1
А
1
Длина вектора ускорения точки В:
2
pab
D
E
aB
3
C
b
aB
a
pa,a,d

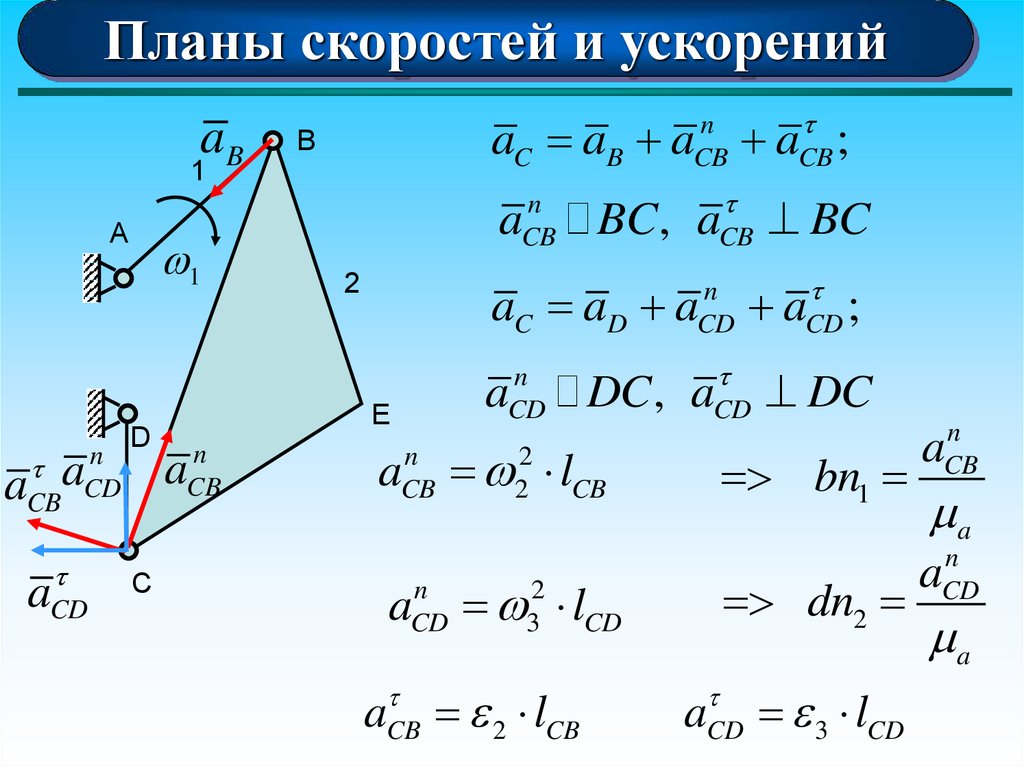
17.

Планы скоростей и ускорений
aB
1
А
n
CD
1
D
aCBa
aCD
C
n
CB
a
2
BC, aCB BC
aC aD a
n
CD
n
CD
a
E
n
aCB
aC aB a aCB ;
n
CB
B
n
CB
a
n
CD
a
aCD ;
DC, aCD DC
lCB
bn1
2
2
dn2
lCD
2
3
aCB 2 lCB
aCD 3 lCD
n
CB
a
a
n
CD
a
a

18.

Планы скоростей и ускорений
aB
aC aB a aCB ;
1
А
n
CD
1
D
aCBa
aCD
n
aC aD aCD
aCD
;
2
E
n
aCB
BC
aCD
c
DC
C
n
CB
B
n2
aÑ
aCB
n
aCD
pa,a,d
n1
n
CB
a
b
aB

19.

Планы скоростей и ускорений
aB
Из плана находим
B
aC pa c a
1
А
1
D
aCBa
aCD
2
2
3
n
CD
aCB
n1c a
2
lCВ
lCB
aCD n2c a
3
lCD
lCD
E
n
aCB
BC
c
DC
C
aCD
n2
aÑ
aCB
n
aCD
pa,a,d
n1
n
CB
a
b
aB

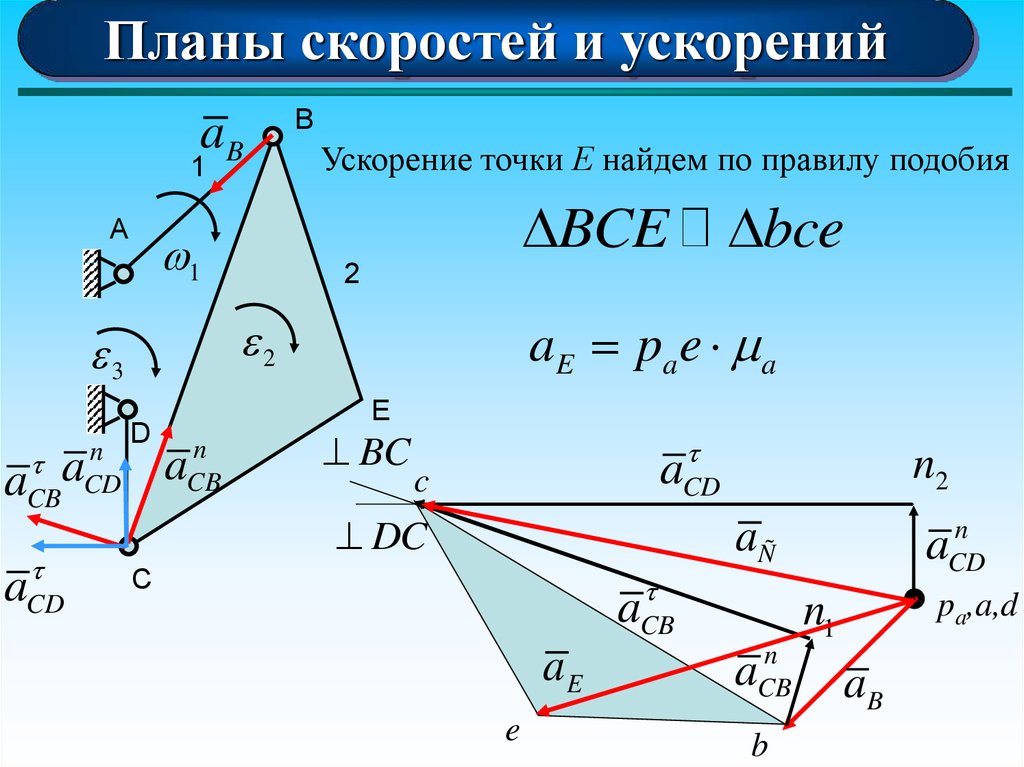
20.

Планы скоростей и ускорений
aB
1
А
D
aCD
bce
2
aE pa e a
2
aCBa
Ускорение точки Е найдем по правилу подобия
BCE
1
3
n
CD
B
E
n
CB
a
BC
aCD
c
DC
n2
aÑ
C
aCB
aE
e
n
CD
a
pa,a,d
n1
n
CB
a
b
aB