Плоский изгиб. Деформации и перемещения. Условие жесткости

1.

ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Инженерно-технический институт
Кафедра прикладной механики
Лекции
по дисциплине «Техническая механика»
270800 - Строительство

2. Плоский изгиб Деформации и перемещения Условие жесткости

3.

ЭНЕРГЕТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА
ДЕФОРМАЦИЙ В УПРУГИХ СИСТЕМ
Потенциальная энергия деформации в общем случае нагружения:
Закон сохранения энергии:
Потенциальная энергия внешних сил UP, действующих на тело,
находящееся в равновесии, полностью переходит в потенциальную энергию
деформации U этого тела:
Потенциальная энергия деформации U численно равна работе внешних сил
AP, проделанной ими при этой деформации:
В балках основным усилием вызывающим деформацию изгиба
является изгибающий момент, поэтому потенциальная энергия упругой
деформации при изгибе балки определяется по:
i
U
0
M x2i dZ
2 EI X

4.

Обобщенные силы и обобщенные перемещения
Потенциальная энергия деформации (или, с другой стороны, работа силы)
численно равна половине произведения величины силового фактора на
значение перемещения, соответствующего этой силе:
Таким образом, появляется возможность решать задачу в общем виде, не
конкретизируя ни силовые факторы, ни перемещения. При этом вводят
понятия обобщенной силы (F) и обобщенного перемещения (Δ).
Обобщенная сила – это сила или группа сил, которую удобно выделить
при подсчете потенциальной энергии деформации. Обобщенной силой
может быть сосредоточенная сила, момент, распределенная нагрузка или
их сочетание.
Обобщенное перемещение – это тот вид перемещения (линейное,
угловое, объемное и т. д.), на котором рассматриваемая обобщенная сила
производит работу.

5.

Выбирать обобщенное перемещение необходимо таким образом,
чтобы произведение обобщенного перемещения на обобщенную силу
представляло собой работу (размерность работы – H·м).
Таким образом, для сосредоточенной силы, принятой за
обобщенную, обобщенным перемещением будет являться линейное
перемещение точки приложения силы.
Если в качестве обобщенной силы выбран момент, то обобщенным
перемещением будет являться угол поворота сечения в точке приложения
момента.
3. Теорема Кастильяно
Обобщенное перемещение сечения упругой системы, где приложена
обобщенная сила равна частному производному от потенциальной энергии
упругой системы по этой обобщенной силе.

6.

4. Метод Максвелла-Мора
Для определить перемещения методом Максвелла-Мора, необходимо:
1) рассмотреть «грузовую» систему, нагруженную только внешними
силами, и записать для этой системы выражения для внутренних усилий по
участкам;
2) рассмотреть «единичную» систему, нагруженную только одной силой –
единичной силой Φ1=1, приложенной в той точке, где требуется найти
перемещение, и записать для этой системы выражения для внутренних
усилий по участкам;
3) подставить найденные внутренние усилия в интеграл Максвелла-Мора и
найти перемещение.
n
l
M xF M x1
dx
EI x

7.

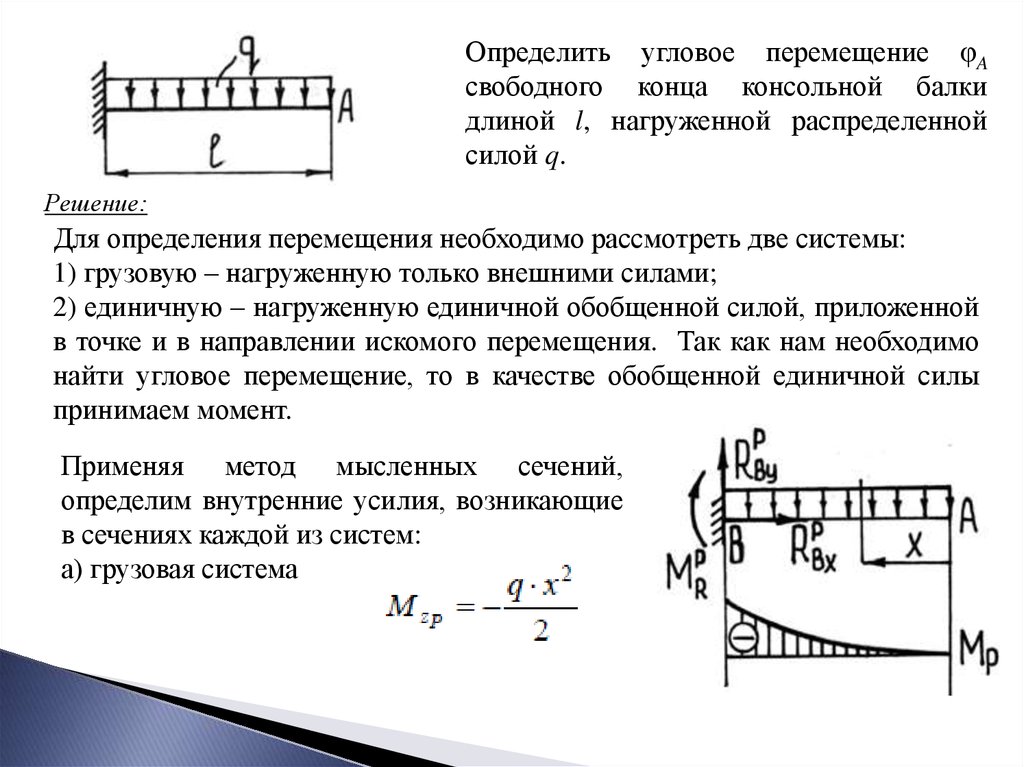
Определить угловое перемещение φA
свободного конца консольной балки
длиной l, нагруженной распределенной
силой q.
Решение:
Для определения перемещения необходимо рассмотреть две системы:
1) грузовую – нагруженную только внешними силами;
2) единичную – нагруженную единичной обобщенной силой, приложенной
в точке и в направлении искомого перемещения. Так как нам необходимо
найти угловое перемещение, то в качестве обобщенной единичной силы
принимаем момент.
Применяя метод мысленных сечений,
определим внутренние усилия, возникающие
в сечениях каждой из систем:
а) грузовая система

8.

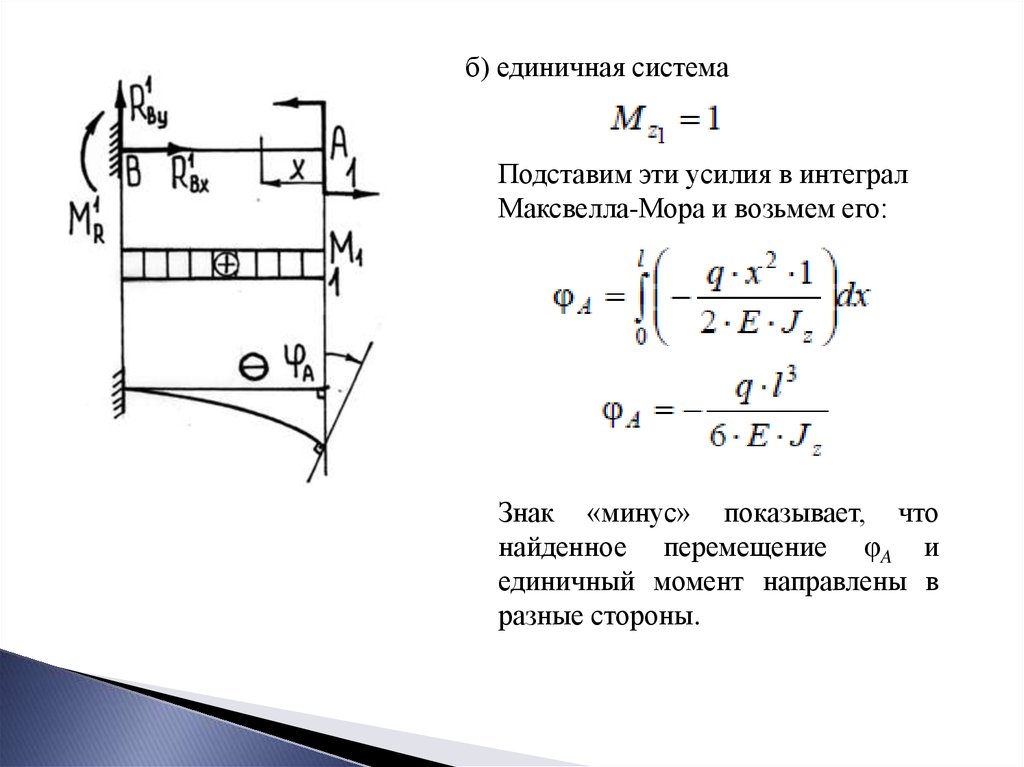
б) единичная система
Подставим эти усилия в интеграл
Максвелла-Мора и возьмем его:
Знак «минус» показывает, что
найденное перемещение φA и
единичный момент направлены в
разные стороны.

9.

5. Формула Симпсона
li
0
M x M1
dz
EI x
l
(
M xн M 1н 4M xC M 1C M xK M 1K )i
6 EI x
M xн , M xC , M xK -значения ординат изгибающих моментов от действия
заданных нагрузок в начале, середине и конце рассматриваемого участка;
M1н , M1C , M1K – значения ординат изгибающих моментов от действия
единичной силы или единичного момента в начале, середине и конце
рассматриваемого участка.

10.

m=6 кН м
a)
q =12кН/м
к
RA
RB
4м
2м
1м
6
1,5
б)
Эпюра M
Для стальной балки на двух шарнирных опорах из двух швеллеров № 30,
+
определить прогиб и 14
угол поворота свободного конца балки формулой
Симпсона.
28
в)
I
34
x
11620см4
38
E 2,1 10
5
RA
г)
Pк =1
8
МПа
2,1
10
кПа
к
RB
0,167 0,333
0,667
1
0,5

11.

Решение:
Формула Симпсона:
MPM1
dz
EI
li
m=6
m=6 кН
кН м
м
q
кН/м
q =12
=12кН/м
R
RB
B
4
4м
м
2
2м
м
+
+
28
28
34
34
Участок 1
R
RA
A
M x Ra z
0,333
0,167
0,167 0,333
38
38
m 0
y 0
RB 46 кН
A
RА 14 кН
1
1м
м
6
6
14
14
Строим эпюру изгибающих
1,5
моментов от заданной нагрузки
1,5
M
кН м
Эпюра
MP
м
Эпюра
P кНэпюру
(грузовую
МР),
определяем значения ординат в
начале, середине и конце
=1
P
Pкк =1
каждого участка.
к
к 2
Участок
R
RB
B
Участок 3
2
z
M x Ra (2 z ) m q
1
2
0,667
1 0,5
0,667
0,5
m
mкк =1
=1
Из условия равновесия балки
определяем опорные реакции:
кк
R
RA
A
li
H
C
k
M PH M 1 4M PC M 1 M Pk M 1
6 EIi
z2
M x q
2
Эпюра
кН м
м
Эпюра M
M кк кН
i

12.

Для определения прогиба
m=6
сечения
за
m=6 кН
кН м
м «К»
кН/м
единичную q
нагрузку
кН/м
q =12
=12
принимаем
кк
сосредоточенную
силу,
R
RAAравную единице и строимR
RB
B
44 м
1
22мм
м
1м
м
эпюру
изгибающих
6 1,5
1,5
моментов с определением
её ординат во всех
++
14
рассмотренных
выше
14
28
28
сечениях.
38
34
34
Pк =1
к
R
RAA
RB
0,333 0,667
0,167
0,167 0,333
1
0,5
mк =1
RA
R
A
RB
Прогиб сечения «К» равен:
li
yk
M P M1
dz
EI
0
li
H
C
k
M PH M 1 4 M PC M 1 M Pk M 1
6 EIi
i
2
0
4
14
0
,
167
28
0
,
333
6
M
M
кН
м
Эпюра
кН
м
Эпюра
P
1 4 P
34
0
,
333
4
38
0
,
667
6
1
EI 6
1
6 1 4 1,5 0,5
6
75,359
75,359
0,31 10 2 м.
8
8
EI
2,1 10 11620 10
Прогиб y имеет отрицательный знак,
сечение
«К»
поднимается
вверх,
против
направления единичной силы.
к
кН м
м
Эпюра
Эпюра
M
M
кк кН
следовательно,

13.

A
.
4м
2м
B
1м
Для
определения
угла
Угол поворота сечения «К» будет:
6 1,5
поворота сечения «К» за
Эпюра MP кН м
li
H
C
k
единичную силу+ принимаем
M PH M 1 4 M PC M 1 M Pk M 1
k
14
6 EIi
единичный
i
28 сосредоточенный
38
момент и34 строим эпюру Pк =1
2
0 4 14 0,1667 28 0,333
изгибающих
моментов к
1 6
(единичная
эпюра)
с
EI 4
RA
RB
6 34 0,333 4 38( 0,667) 6 1
определением её ординат во
всех
рассмотренных
1
1
0,667
0,333
0,5 6 1 4 1,5 1 0
0,167
сечениях.
6
Эпюра M к кН м
75,32
75,32
0,31 10 2 рад.
mк =1
8
8
EI
RA
0,1667
RB
0,333
0,667
1 1 1
2,1 10 11620 10
Угол
поворота
к
имеет
отрицательный
знак,
Эпюра
M к кН м
следовательно,
сечение
«К»
поворачивается
против
хода
часовой
стрелки
против
направления единичного момента.

14.

6. Способ Верещагина
Если балка в пределах рассматриваемого участка имеет постоянное
сечение, площадь эпюры изгибающих моментов и положение её центра
тяжести легко определяемы, то интеграл Максвелла - Мора может быть
решен графоаналитическим методом Верещагина:
n
M 1C
EI x
где ω – площадь «грузовой» эпюры MF на данном участке; M1C – величина
«единичного» момента под центром тяжести «грузовой» эпюры на данном
участке.

15.

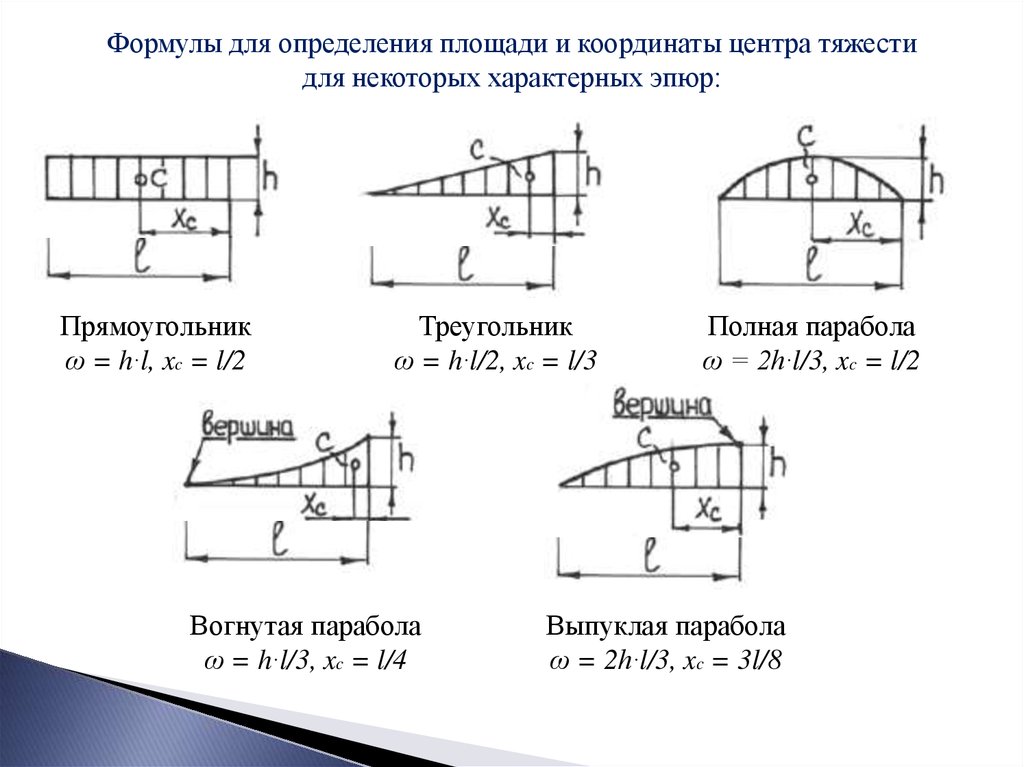
Формулы для определения площади и координаты центра тяжести
для некоторых характерных эпюр:
Прямоугольник
ω = h·l, xc = l/2
Треугольник
ω = h·l/2, xc = l/3
Вогнутая парабола
ω = h·l/3, xc = l/4
Полная парабола
ω = 2h·l/3, xc = l/2
Выпуклая парабола
ω = 2h·l/3, xc = 3l/8

16.

Для деревянной балки прямоугольного сечения 20 20 см2 определить
вертикальное перемещение оси балки в середине пролета и угол поворота
опорного сечения А методом Верещагина.
a)
q =10 кН/м
A
к
RA
RB
4м
z с =1,5 м
б)
B
ц.т.
E 0,11 10 МПа
ц.т.
+ I x 13333,33 см
5
P
1
1,5 м
qL 2
8
4
P
2
MP

17.

Решение:
MP Mk
P M kC
При применении формулы Верещагина кр
dz (
)i
li
i
0
q =10 кН/м
A
B
к
RA
RB
4м
z с =1,5 м
P
ц.т.
1
1,5 м
MP
ц.т.
+
P
qL 2
8
2
i
EI
Балка имеет два равных участка АК и КВ.
Площади эпюр:
l
2
к
P1 P2
RB
Положение центров тяжести этих
площадей определяем: Mк
Mкс1= 0,75
i
для определения перемещений сечения
балки строим эпюру изгибающих
моментов
от
заданной
нагрузки
(грузовую эпюру), определяем площади
эпюр и положение их центров тяжести
на соответствующих участках.
P =1
RA
EI
i
+
P
4
L
Mкс 2= 0,75
ql 3
M P z dz
26,67
24
0
l
2
M z zdz
p
zC
0
P1
5 l
1,25 м.
8 2

18.

q =10 кН/м
Для определения прогиба
Ординаты единичной эпюры под
A
B
в
сечении
«К»
за
центрами тяжести этих площадей равны:
к
единичную
нагрузку
R
RB
A
принимаем 4 м
C
5 P l
C
M
M
0,625
k
2
k1
сосредоточенную
z с =1,5 м
1,5 м
8 4
единичную силу строим
MPПрогиб сечения «К» равен:
ц.т.
эпюруц.т. + изгибающих
P
моментов
от действия
P
1
C
C
1
y
M
M
k
k2
2
1
k
P
P
1
2
этой силы.
qL 2
EI
8
P =1
Mкс1= 0,75
Орд
EI
33.3375
0,11 108 13333,33 10 8
2,273 10 2 м.
к
RA
26,67 0,625 2
RB
Mк
+
P
L
Mкс 2= 0,75
4
mA=1
RA
RB
C
MA =-0,5
уk
имеет
положительный
знак,
следовательно, прогиб сечения «К»
балки направлен вниз, т.е. совпадает с
направлением единичной силы.

19.

)
)
)
)
)
1,5 м
с
ц.т.
MP
ц.т.
+
Для определения
угла поворота
P
«А» за
опорного
1 сечения балки P
2
2
qL
единичную
силу
принимаем
8
сосредоточенный
единичный
=1
P
момент,
приложенный
в
рассматриваемомк сечении,
и
RA
RB
строим
эпюру
изгибающих
моментов от его действия.
Mк
Для этой
задачи
балка
имеет
один
+
с = 0,75
с = 0,75
M
M
к
к
участок.
1
P L 2
4
mA=1
Площадь эпюры МР:
.
.
l
ql 3
P M P zdz
53,33
12
0
Так как эпюра МР симметричная, то
центр
тяжести
площади
р
находится посередине. Ордината
единичной эпюры под центром
тяжести этой площади равна:
C
1
M A 1 0 ,5
2
Угол поворота сечения «А» равен:
M A 53,33 ( 0,5)
кр A P
EI
EI
26,67
1,82 10 2 рад
8
8
0,11 10 13333,33 10
C
RA
RB
C
1
MA =-0,5
MA
Угол поворота А имеет отрицательный знак,
следовательно, сечение поворачивается по ходу часовой
стрелки (против направления единичного момента).

20.

Условие жесткости
Под расчетом на жесткость понимают оценку упругой податливости балки
под действием приложенных нагрузок и подбор таких размеров
поперечного сечения, при которых перемещения не будут превышать
установленных нормами пределов.
f м акс f
l
400...800
Перемещение центра тяжести сечения по направлению перпендикулярному к
оси балки, называется прогибом.
Наибольший прогиб в пролете или на консоли балки, называется стрелой
прогиба и обозначается - f.