Оптимизация контуров регулирования

1. Оптимизация контуров регулирования

Цель оптимизации- поиск регулятора при
котором выходной сигнал контура будет
способен повторять задающее воздействии
без больших колебаний, а действие
возмущения будет нейтрализовано.

2. Оптимизация контуров регулирования

При единичной обратной связи
W pWo
Х вых ( р )
W p ( р)
Wз ( р )
Х вх ( р ) 1 W p ( p ) 1 W pWo
з
При наличии датчика обратной связи
Идеальный режим
Х вых (p)
з
1 Wз ( р ) 1
X з ( р)
Х вых (p)
з
0 Wвозм
( р) 0
X возм (р)
Wз з (р)
Wпк (р)
1 W p ( p)
Wp Wo
1 Wp Wo Wдос
Решение идеальной задачи ступает в противоречие с техническими
возможностями и экономической целесообразностью. На практике
инерционность объекта компенсируют насколько это возможно и
насколько это целесообразно. В контуре оставляют малую
инерционность для сохранения помехоустойчивости контура.

3. Оптимизация контуров регулирования

Передаточные функции замкнутых систем АЭП
1.
Wз з ( j )
Wз з (р)
bo
a o a1p a 2 p 2
2.
Wз з (р)
b0
(a 0 2 a 2 ) 2 2 a 1 2
Wз з ( j ) 1
b0
a 0 2 2 (a12 2a 0 a 2 ) 4 a 2 2
при 2а0а2 = а12
b 0 b1p
a 0 a 1p a 2 p 2 a 3 p 3
Wз з ( j ) 1
при 2а0а2 = а12 2а1а3 = а22

4. Оптимизация контуров регулирования

Оптимизация на модульный оптимум.
1. Объект контура содержит большую (То) и малую (Тµ)
инерционности:
ko
Wo (p)
(To p 1)(T p 1)
Для компенсации большой инерционности и для придания
контуру астатических свойств нужен ПИ регулятор,
Т из р 1 ,у которого: Тиз= То, а Кр=?
W ( p) k
p
Найдем
p
Т из р
W p ( p ) Wo ( p )W p ( p )
k p (Tиз р 1)
ko k p
ko
(To p 1)(T p 1)
Т из р
To p (T p 1)

5. Оптимизация на модульный оптимум

.
Передаточная функция замкнутого контура:
kok p
Wp p ( p)
To p(T p 1)
Wпк ( р)
Wз ( р)
kok p
1 Wпк ( р) Woc ( p)
1 Wp p ( p)
1
To p(T p 1)
з
ko k p
ko k p To p ToT p 2
где
k0kp = b0 = a0; T0 = a1; T0T = a2.
Из условия оптимизации на модульный оптимум: 2a0a2 = a12,
запишем 2kpk0T0T = T02; Откуда находим: k p To
2k o T
После подстановки имеем:
ko
Wз з (р)
ko
To
2k o T
To
To p To T p 2
2k o T
1
1 2T p 2T 2 p 2

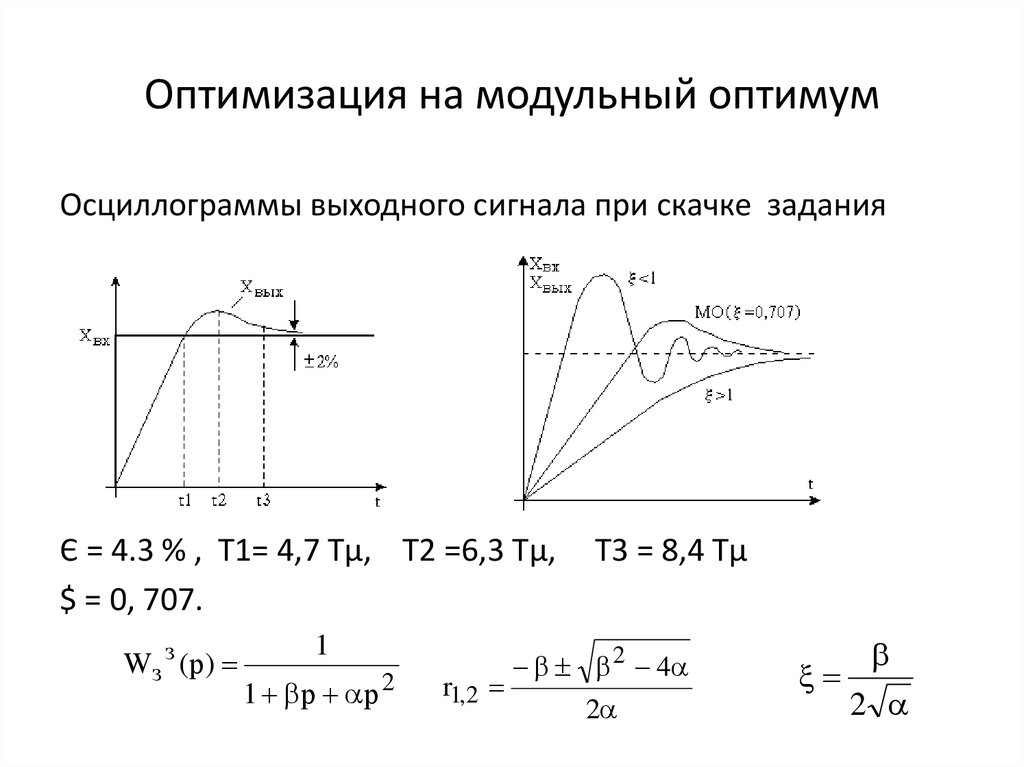
6. Оптимизация на модульный оптимум

Осциллограммы выходного сигнала при скачке задания
Є = 4.3 % , Т1= 4,7 Тµ, Т2 =6,3 Тµ,
$ = 0, 707.
з
Wз (р)
1
1 р р 2
Т3 = 8,4 Тµ
2 4
r1,2
2
2

7. Оптимизация на модульный оптимум

ЛАЧХ контура, оптимизированного на МО.
W р(мо ) (р)
ko
Т р 1
ko
k p из
(To p 1)(T p 1)
Т из р
(To p 1)(T p 1)
To
(To p 1)
2k o T
To p
з(мо )
Wз
( р)
1
;
2T p(T p 1)
W р(мо ) (р)
1 W р(мо ) (р)
з(мо)
Wз
(р)
1
1 2T
1
2T p(T p 1)
1
1
2T p(T p 1)
1
1 2T p 2T 2 p 2

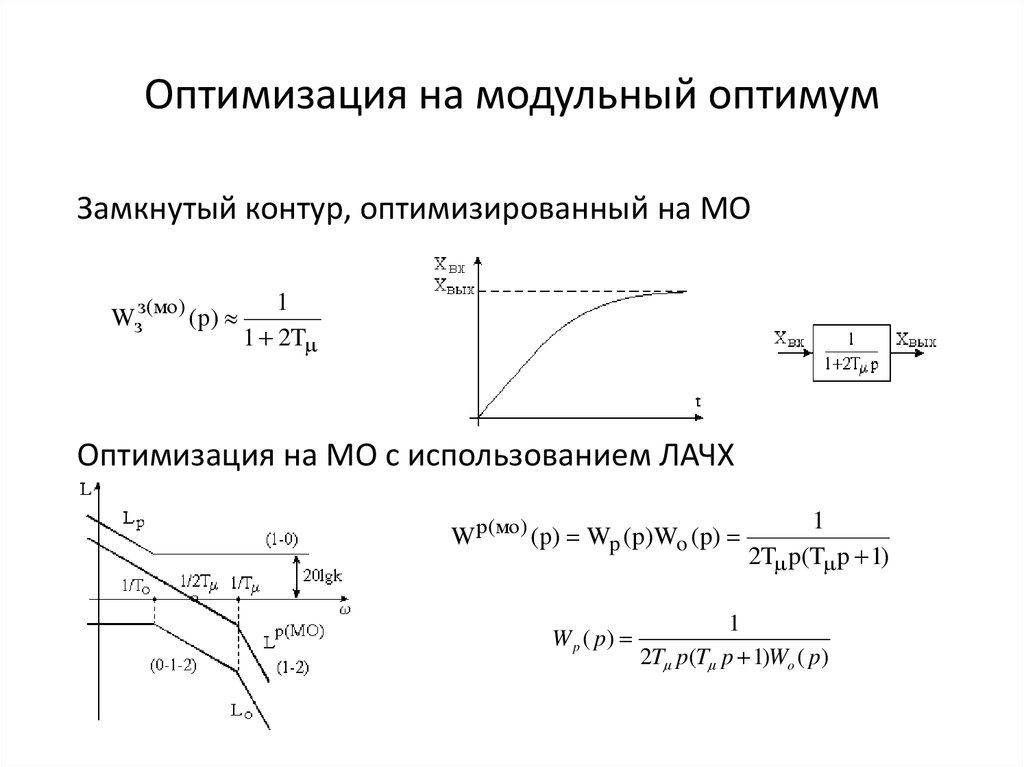
8. Оптимизация на модульный оптимум

Замкнутый контур, оптимизированный на МО
з(мо)
Wз
(р)
1
1 2T
Оптимизация на МО с использованием ЛАЧХ
W р(мо) (р) Wp (p) Wo (p)
W p ( p)
1
2T p(T p 1)
1
2T p (T p 1)Wo ( p )

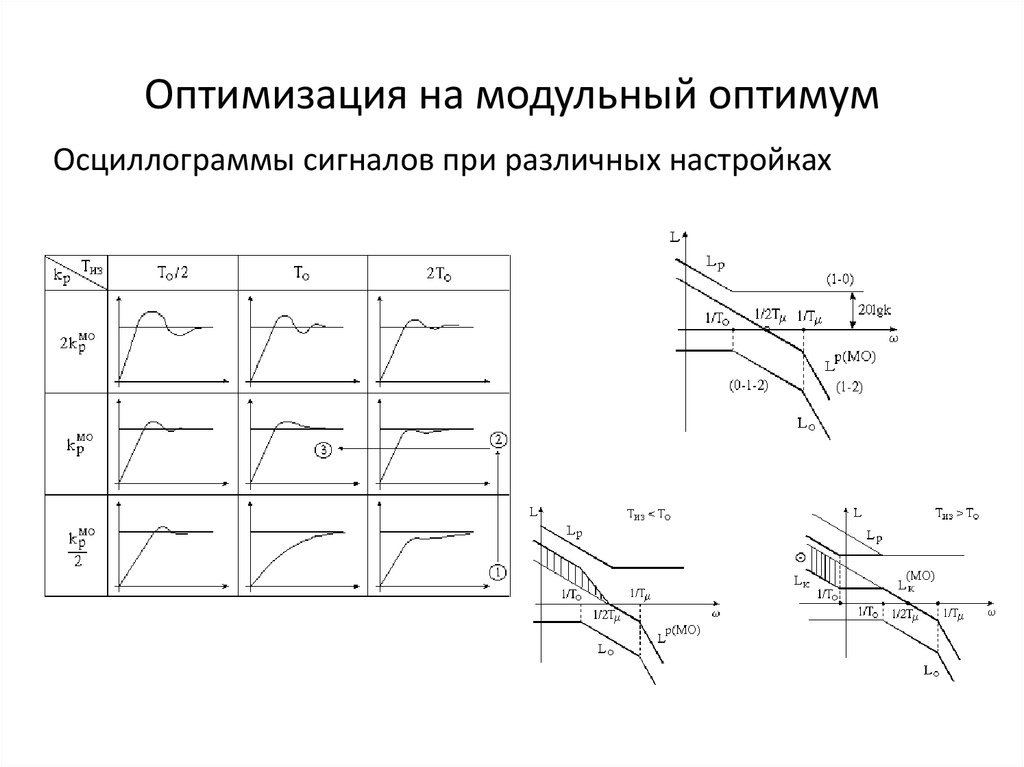
9. Оптимизация на модульный оптимум

Осциллограммы сигналов при различных настройках

10. Оптимизация на модульный оптимум

Ошибка регулирования при настройке на МО
Wош (р)
Х(р) Х вх (р) Х вых (р)
1
1 Wзз (р) 1
2 2
Х вх (р)
Х вх (р)
1 2T p 2T p
2T p 2T 2 p 2
1 2T p 2T 2 p 2
;
lim Wош (р) 0
p 0
Х(р) = WОШ (р) ХВХ (р).

11. Оптимизация на модульный оптимум

2. Оптимизация контура на МО в объекте которого
интегрирующее звено и звено с малой постоянной времени
To
ko
1
W
(
p
)
kp
W (p) Wp (p) Wo (p) Wp (p)
p
2k o T
To p(T p 1) 2T p(T p 1)
p
Получили регулятор П типа, при котором контур в общем
случае -статический.
По заданию контур –астатический (т.к. есть интегрирующее
звено в объекте).
По возмущению –м.б. как статическим, так и астатическим.

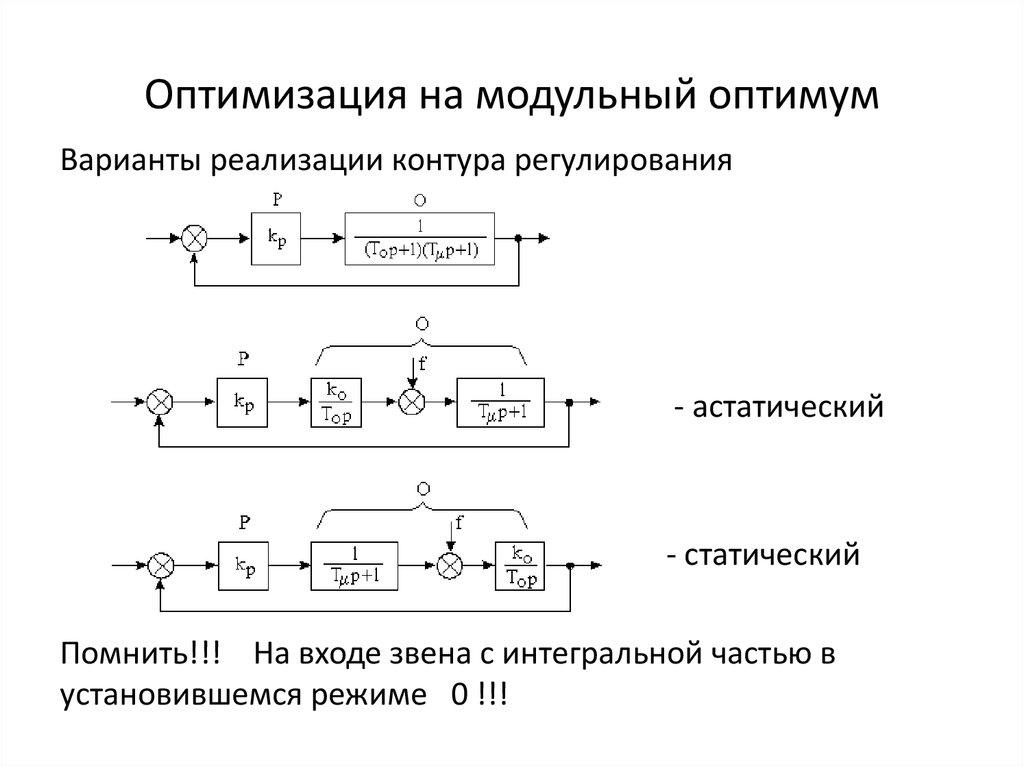
12. Оптимизация на модульный оптимум

Варианты реализации контура регулирования
- астатический
- статический
Помнить!!! На входе звена с интегральной частью в
установившемся режиме 0 !!!

13. Оптимизация контура на симметричный оптимум

Построение астатической контура в объекте которого
интегрирующее звено и звено с малой постоянной времени.
Т из р 1
Надо применить ПИ –регулятор:
Wp k p
Т из р
Т р 1
ko
W p (p) k p из
Т из р To p(T p 1)
2а0а2 = а12 2kpk0ТИЗТ0 = kp2k02ТИЗ2 2Т0 = kpk0ТИЗ;
2а1а3 = а22 2kpk0ТИЗ2Т0Т = ТИЗ2Т02 2kpk0T = T0;
k p k o (Т из р 1)
kp
2
Т
Т
р
(Т р 1)
из
o
W з ( р)
p
k
k
(
Т
р
1
)
p o из
1 W
1
Т изТ o р 2 (Т р 1)
Wp
2To
k p k o k p k o Tиз р
2
k p k o k p k o Т из р Т изТ o р Т изТ o Т р
3
;
To
2k o T
To
k o Т из
2k o T
ТИЗ = 4Т ;

14. Оптимизация контура на симметричный оптимум

Подстановка полученных Кр и Тиз позволяют получить:
4T p 1
4T p 1
Тo
ko
1
W ( р)
2k o T 4T p To p(T p 1)
4T p 2T p(T p 1)
р
Wзз (р)
1 4Т р
1 4Т р 8Т 2 р 2 8Т 3 р 3
Т1=3,1 Тµ, Т2 = 5,8 Тµ, Т3 = 16,5Тµ
Название настройки – по виду ЛАЧХ
(частота среза симметрична частотам сопряжения)

15. Оптимизация контура на симметричный оптимум

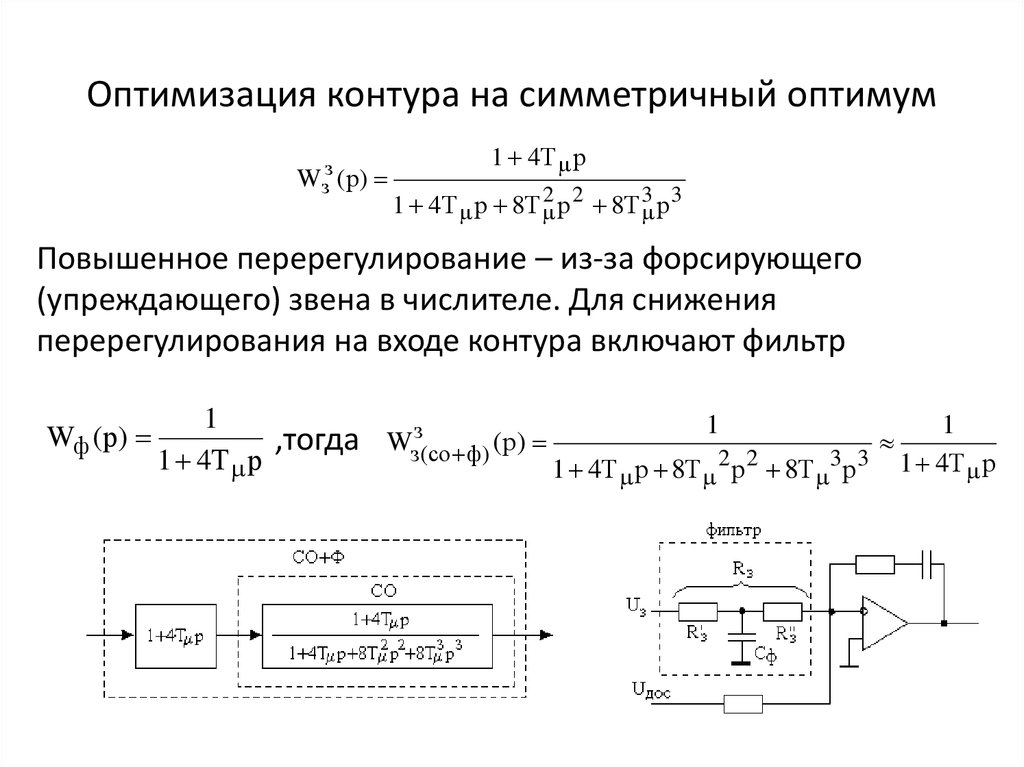
Wзз (р)
1 4Т р
1 4Т р 8Т 2 р 2 8Т 3 р 3
Повышенное перерегулирование – из-за форсирующего
(упреждающего) звена в числителе. Для снижения
перерегулирования на входе контура включают фильтр
Wф (р)
1
1
1
,тогда Wзз(со ф) (р)
1 4Т р
1 4Т р 8Т 2 р 2 8Т 3р 3 1 4Т р

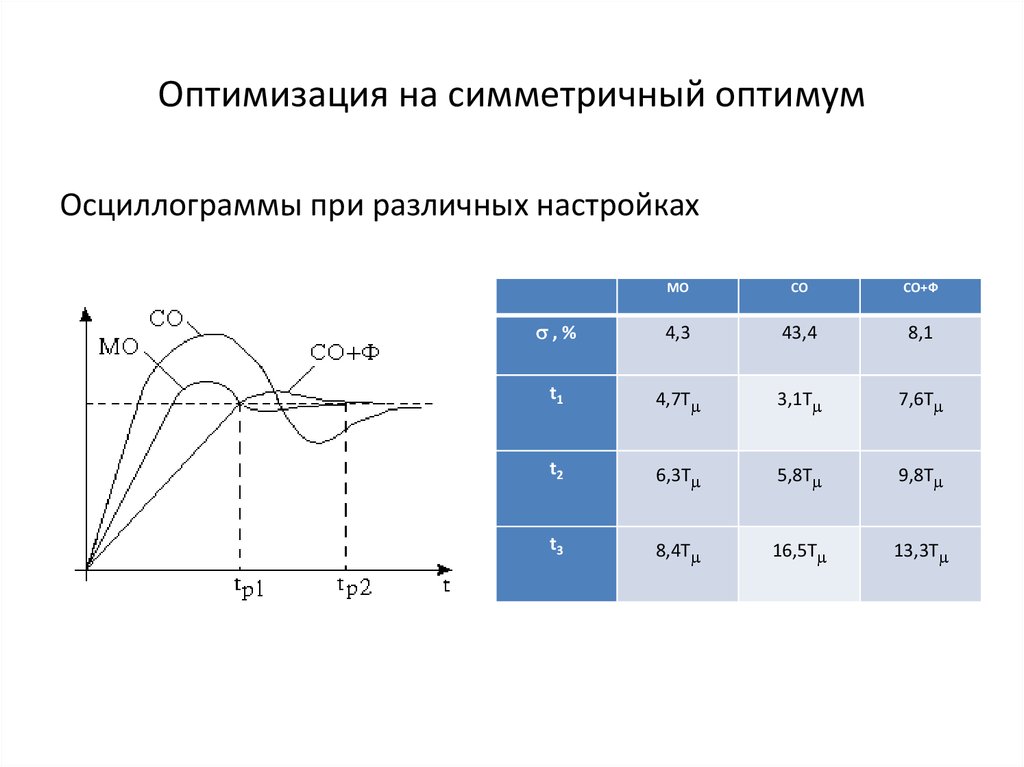
16. Оптимизация на симметричный оптимум

Осциллограммы при различных настройках
МО
СО
СО+Ф
,%
4,3
43,4
8,1
t1
4,7Т
3,1Т
7,6Т
t2
6,3Т
5,8Т
9,8Т
t3
8,4Т
16,5Т
13,3Т