Похожие презентации:
Элементы математического анализа
1. Элементы математического анализа
Лекционное занятиеВ группах 12ПОэ, 12ЭТТМКн
Преподаватель Усенко Т.И.
2. План
1)2)
3)
4)
5)
6)
7)
8)
9)
Последовательность
Понятие функции
Различные способы задания функции
Предел функции
Теоремы о пределах функции
Два замечательных предела
Бесконечно большие и малые функции
Понятие сложной и обратной функции
Понятие неявно заданной функции
3. Последовательность
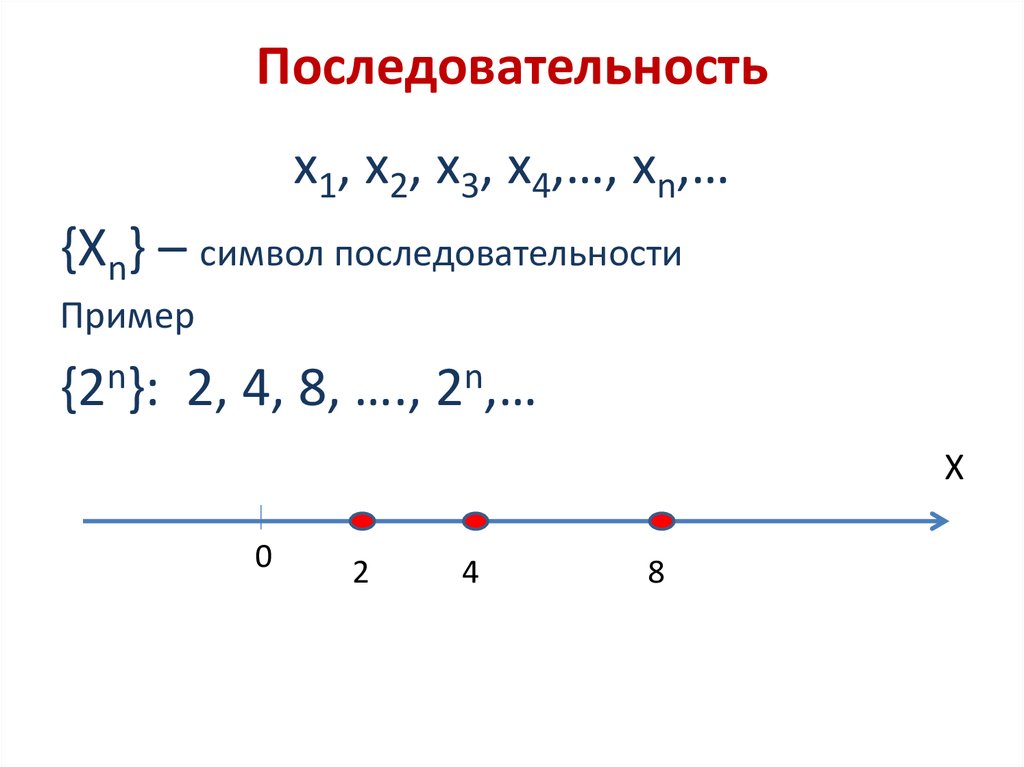
х1, х2, х3, х4,…, хn,…{Xn} – символ последовательности
Пример
{2n}: 2, 4, 8, …., 2n,…
Х
0
2
4
8
4. Арифметические действия над числовыми последовательностями
1.2.
3.
4.
m {Xn} = {mXn}
{Xn} + {Yn} = {Xn + Yn}
{Xn} - {Yn} = {Xn - Yn}
{Xn} · {Yn} = {Xn · Yn}
Xn Xn
5.
Yn Yn
5. Ограниченные и не ограниченные последовательности
Xn ≤ M(-∞; M]
( X n ≥ m)
( [m; ∞) )
________________________________________________________________________
m ≤ Xn ≤ M
[m; M]
____________________________________________________________________________________
| Xn | > A
Xn > A или Xn > - A
(- ∞; ∞ )
6. Примеры
1) 1, 2, 3,…, n,...2) -1, -2, -3, …, -n, …
3) 1, ⅟2, ⅓, … , ⅟n, …
4) -1, 2, -3, …, (-1)n·n
7. Бесконечно большие и бесконечно малые последовательности
{Xn}A > 0, N при n > N
{n}: 1, 2, 3, …, n, …
Последовательность
| Xn | > A
__________________________________________________________________________________________
Последовательность {an}
Ɛ > 0, N при n > N
| an | < Ɛ
{⅟n}: 1, ⅟2, ⅓, … , ⅟n, …
8. Свойства
1. Если {Xn} б. б., то2. Если {an} б. м., то
{⅟Xn} б. м.
{⅟an}
б. б.
3. Если {Xn} +{an} б. м. , то {Xn + an} б. м.
4. Если {Xn} +{an} б. б. , то {Xn + an} б. б.
5. Если {Xn} ·{an} б. м., то {Xn · an} б. м.
6. Если {Xn} огр-ная, {an} б. м., то {Xn · an} б. м.
9. Сходящиеся последовательности
a – предел последовательности {Xn}Ɛ > 0, N при n > N
| Xn - a | < Ɛ
Xn
a
lim
x
a
n
n
10. Свойства
1. Если {an} б. м. и an = с, то с = 0.2. Сходящаяся последовательность имеет
только один предел
3. Если {Xn} +{Yn} сх-ся , то {Xn + Yn} an.
lim
Xn lim
Yn
Xn Yn lim
n
n
n
4. Если {Xn} ·{an} сх-ся, то {Xn · an} сх-ся.
lim
X
Y
lim
X
lim
Y
n
n
n
n
n
n
n
5. Если Xn
Yn
сх-ся, то
Xn
Y
n
сх-ся.
Xn
lim
n
Yn
Xn
lim
n
Yn
lim
n
11. Понятие функции
Множествоf : {<x; y>}
X Є X, y Є Y
y = f (x), y = g (x), y = y (x), y = F(x)
12. Свойства
1) f(x) = C2) y = f(x), xЄ X
f(x) ≤ M (f(x) ≥ m)
3) y = f(x)












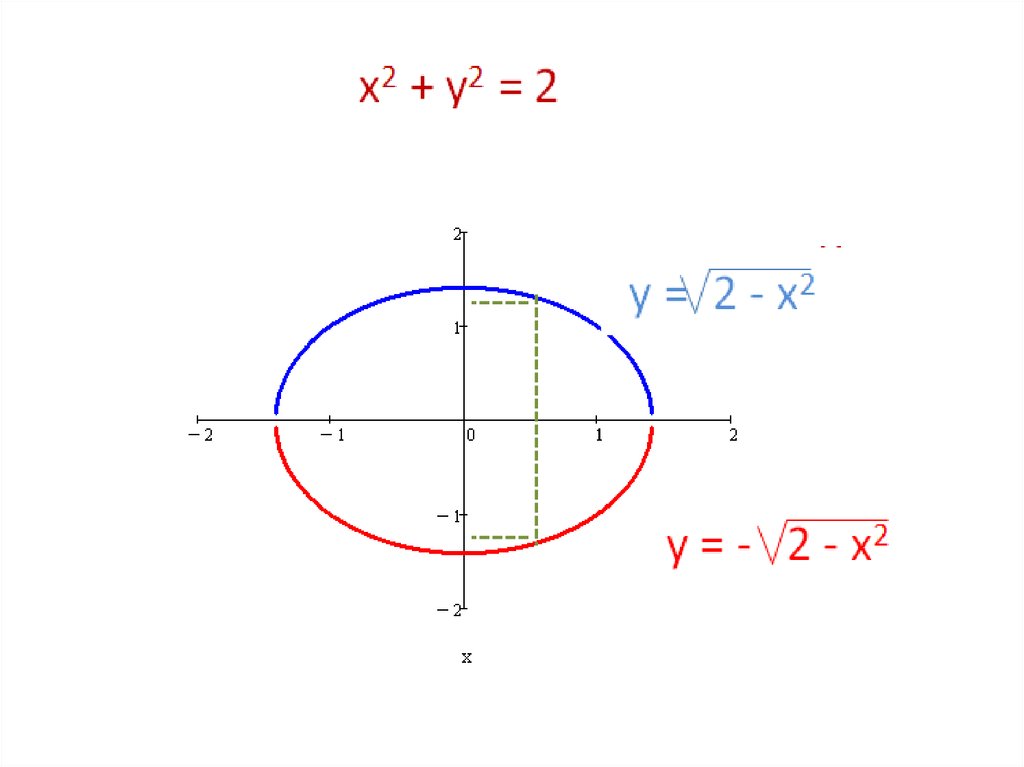
 Математика
Математика








