A combined vision-robot arm. System for material assortment

1. A Combined Vision-Robot Arm System for Material Assortment

By
Prof. Dr. Erol UYAR
R.A. Aytac GOREN
Mech. Eng. (M.Sc.) Alper AYBERK

2. Contents:

• Introduction
• Object Recognition via Classical Moments
• Control of a Robot Arm System
• Conclusion

3. Introduction

• In this project, an application of computer image processing to
recognize various objects and the vision-based guidance of a
robot arm to assort them are investigated.
• Captured image of the passing objects on the conveyor band
are digitalized and features of the objects are calculated to
identify them.
• After identification process, objects are assorted by a built up
revolute jointed robot manipulator with five degrees of freedom
with a gripper, as an end-effector, is used to assort the recognized
objects to desired locations via a predefined trajectory.

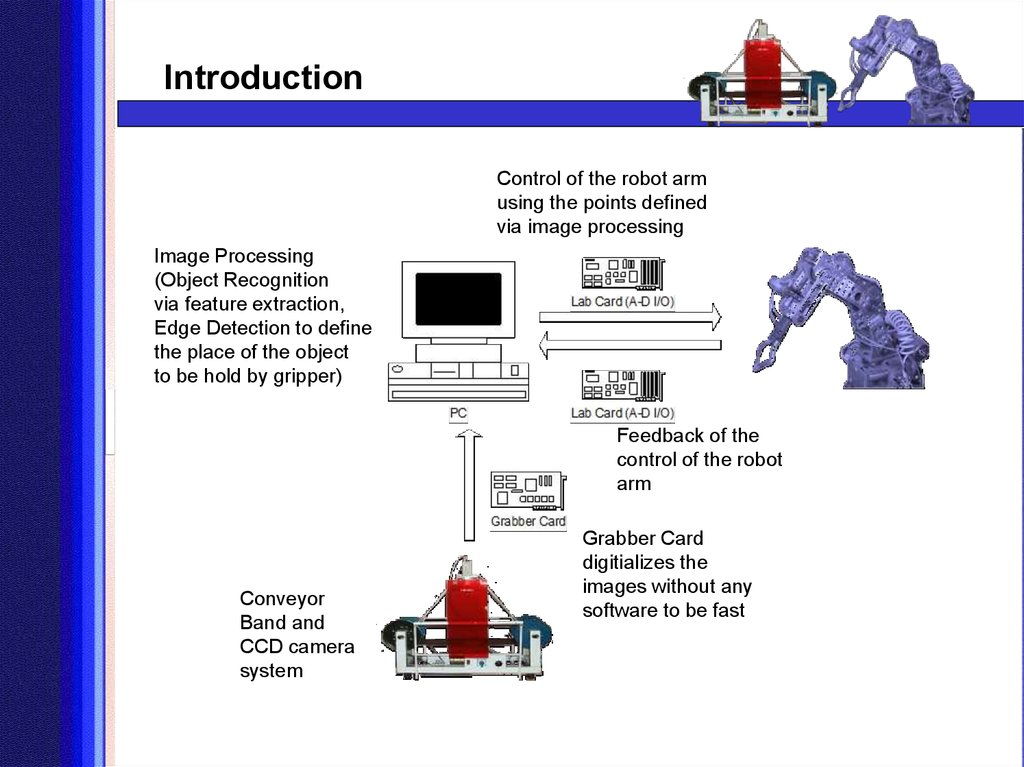
4. Introduction

Control of the robot arm
using the points defined
via image processing
Image Processing
(Object Recognition
via feature extraction,
Edge Detection to define
the place of the object
to be hold by gripper)
Feedback of the
control of the robot
arm
Conveyor
Band and
CCD camera
system
Grabber Card
digitializes the
images without any
software to be fast

5. Image Processing via Classical Moments

• After Hu presented moment invarients in 1962, they are widely
used in many applications. Subsequently, Resis revised and Li
reviewed and re-formulated, also produced higher order
invariants. However, increasing complexity with increasing order
and having redundant information because of not being derived
from a family of orthogonal functions are the two main drawbacks
of Hu moment invariants.
• Afterwards, in term of noise sensitivity, image description
capability and redundancy of information Legendre moments,
ortogonal moments, geometrical moments, Zernike moments,
pseudo-Zernike moments and Orthogonal Fourier-Mellin
moments are evaluated.

6.

Image Processing via Classical Moments
Central Moment of an Area:
pq ( x x) p ( y y ) q f ( x, y)
(1)
x y
Whereas;
m
x 10
m00
and
m01
y
m00
If we calculate the central moments to the third order
via using the equation (1), we have the following results:
10 ( x x)1 ( y y)0 f ( x, y)
x y
11 ( x x)1 ( y y )1 f ( x, y )
x y

7.

Image Processing via Classical Moments
20 ( x x) 2 ( y y) 0 f ( x, y)
02 ( x x)0 ( y y) 2 f ( x, y)
12 ( x x)1 ( y y) 2 f ( x, y)
22 ( x x) 2 ( y y) 2 f ( x, y)
03 ( x x)0 ( y y)3 f ( x, y)
30 ( x x)3 ( y y )0 f ( x, y )
x y
x y
x y
Denoting
and
x y
x y
x y
as in the following formulas,
Hu moments can be found.
pq
pq
00
1 20 02
p q
1
2
(2)
2 ( 20 02 ) 2 4 112
(3)
3 ( 30 3 12 ) 2 (3 21 03 ) 2
(4)

8.

Image Processing via Classical Moments
4 ( 30 12 ) 2 ( 21 03 ) 2
(5)
5 ( 03 3 12 )( 30 12 ) 03 12 2 3 21 03 2
(3 21 03 )( 21 03 ) 3 30 12 21 03
2
2
(6)
6 ( 20 02 ) 30 12 2 21 03 2
4 11 30 12 21 03
(7)
Six of these invariants are invariable if the image is mirrored. But
the last changes its sign. There were no two patterns those are
the mirror of each other. Thus, the first six moments are used for
object recognition.

9.

Image Processing via Classical Moments
Zernike Moments:
Zernike polynomials, form a complete orthogonal set over the
interior of the unit circle x2+y2=1 . The Zernike function of order (p,
q) is defined in the polar coordinate (r, ) as:
Wpq (r, ) Rpq (r )eiq
(8)
where,
R p , q (r )
B pqk
p
B
rk ,
(9)
( 1)( p k ) / 2 (( p k ) / 2)!
(( p k ) / 2)!((q k ) / 2)!((k q) / 2)!
(10)
pqk
k q , p |k | even

10.

Image Processing via Classical Moments
Zernike moments of order p with repitation q for a digital image is
the projections of the image function onto defined orthogonal basis
functions (8),(9),(10) and can be shown as:
Z pq
p 1
f ( x, y)W
Note that,
x
*
pq
(r , ) x y
(11)
y
W (r, ) Wp, q (r, )
*
pq
and thus
Z *pq Z p, q
r is the length of the vector from origin to pixel (x ,y ) and θ is the
angle between vector r and the x -axis in the counter-clockwise
direction. x2+y2=1, x =r cos θ y=r sin θ.

11.

Image Processing via Classical Moments
Orthogonal Fourier-Mellin Moments:
r is the length of the vector from origin to pixel (x ,y ) and θ is the
angle between vector r and the x -axis in the counter-clockwise
direction. x2+y2=1, x =r cos θ y=r sin θ.
2
Fpq
p
iq
r
f
(
r
,
)
e
rdrd
where q=0,±1, ±2,...
0 0
Then the discrete version of the Fourier-Mellin Moments and
Orthogonal Fourier-Mellin moments can be defined as:
Fpq f ( x, y ) r p e iq x y
x
y

12.

Image Processing via Classical Moments
O pq
p 1
f ( x, y)Q
x
p
(r )e iq x y
y
The magnitude of Hu moments, OFMMs and ZMs are rotation,
translation and scaling invariant features of the captured images.
In this respect, in application of the feature extraction, identifying
and recognizing an object in a class, normalization must be made
for scale invariance. Describing a circle and investigating if the
feature of an object belongs to this circle or not is a way to have
rotation invariance and to define an object in a similarity region.

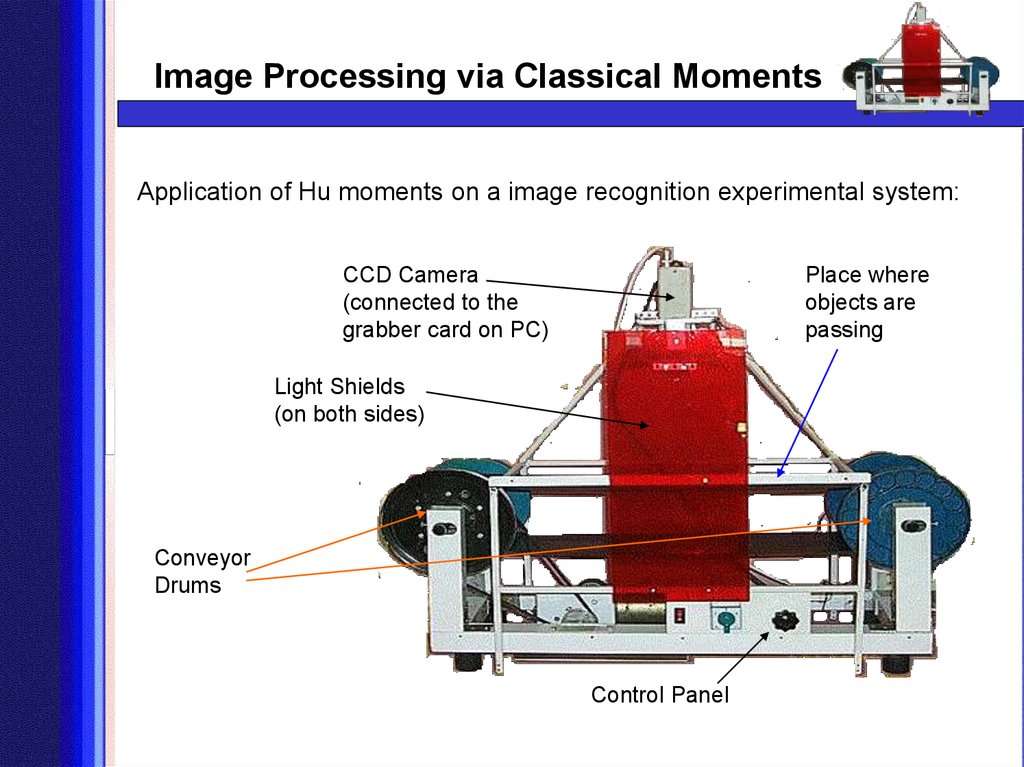
13. Application of Hu moments on a image recognition experimental system:

Image Processing via Classical Moments
Application of Hu moments on a image recognition experimental system:
CCD Camera
(connected to the
grabber card on PC)
Place where
objects are
passing
Light Shields
(on both sides)
Conveyor
Drums
Control Panel

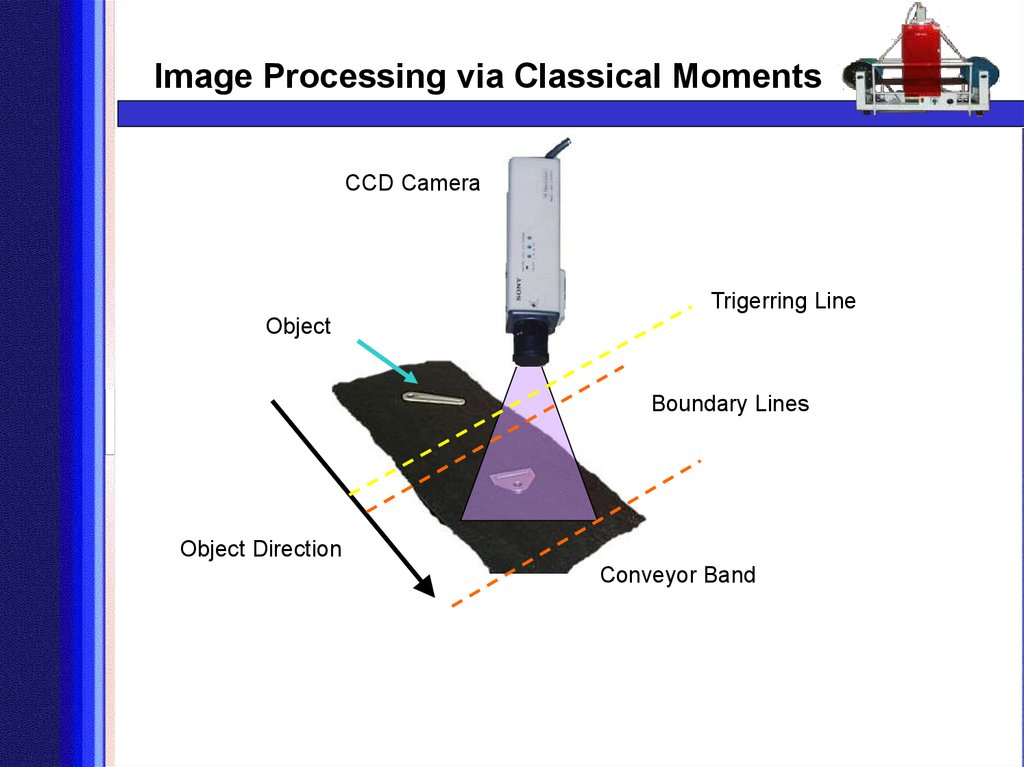
14. CCD Camera

Image Processing via Classical Moments
CCD Camera
Trigerring Line
Object
Boundary Lines
Object Direction
Conveyor Band

15.

Image Processing via Classical Moments
In this project, four types of image processing
techniques are used:
1. Image Data Reduction
2. Segmentation
3. Feature Extraction
4. Object Recognition

16.

Image Processing via Classical Moments
1
Image Data Reduction
a. Digital Conversion:
It reduces the number of gray levels used by the machine
vision system. For example,as we have used in the project, an
8-bit register used for each pixel would have 256 gray levels.
b. Windowing
It involves using only a portion of the total image stored in the
frame buffer for image processing and analysis. In this project,
we used windowing in choosing a smaller area for better
feature extraction.

17.

Image Processing via Classical Moments
2. Segmentation
a. Edge Detection
In Edge Detection it is considered that the intensity change
which occurs in the pixels at the boundary or edge of a part.
Given that a region of similar attributes has been found, the
boundary shape is unknown, the boundary can be determined
via a simple edge following procedure.
Canny Edge Detection Algorithym is used in this project in
order to find the coordinates of the recognized object to handle
by the robot arm.
b. Tresholding

18.

Image Processing via Classical Moments
Some examples of Canny Edge Detection Algorithym can be seen
below

19.

Image Processing via Classical Moments
2. Segmentation
a. Edge Detection
b. Tresholding
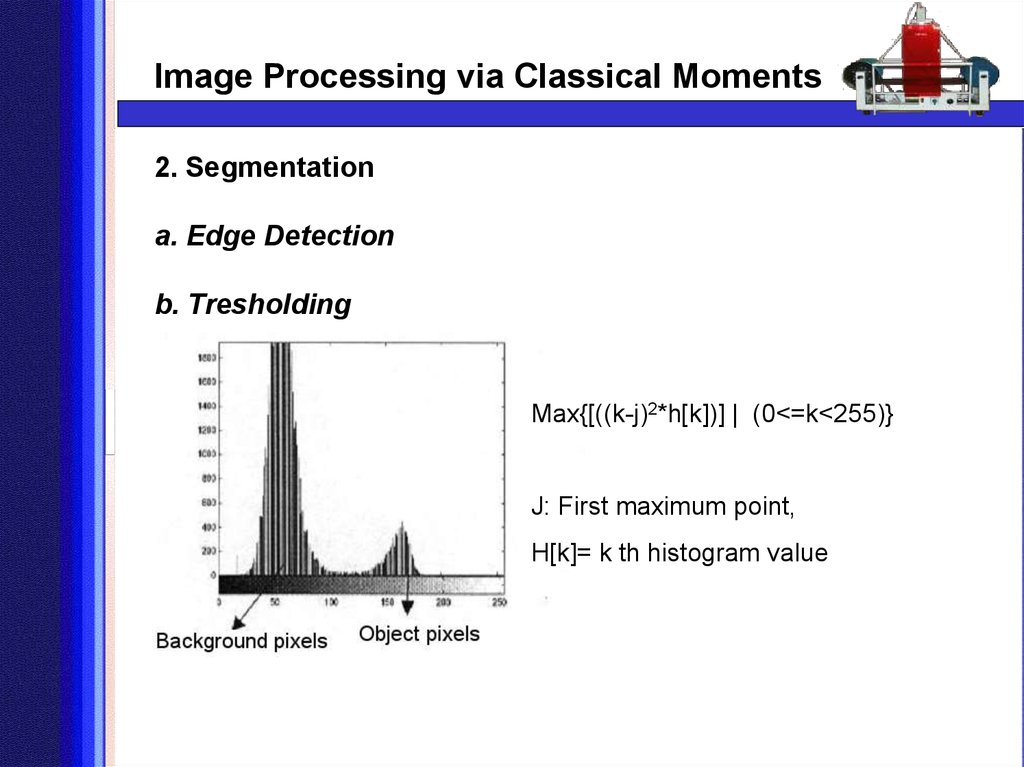
Tresholding is a binary conversion technique in which each
pixel is converted into a binary value, either black or white.
This is accomplished by utilizing a frequency histogram of the
image and establishing what intensity(gray level) to be the
border between black and white.
In this project,adaptive tresholding is used to define the object
area and the background area before feature extraction.

20.

Image Processing via Classical Moments
2. Segmentation
a. Edge Detection
b. Tresholding
Max{[((k-j)2*h[k])] | (0<=k<255)}
J: First maximum point,
H[k]= k th histogram value

21.

Image Processing via Classical Moments
Images of some of the objects, tresholded images and histograms
of the real object onthe background can be seen in figure.

22.

Image Processing via Classical Moments
3. Feature Extraction
Hu moments, Legendre moments, ortogonal moments, geometrical
moments, Zernike moments, pseudo-Zernike moments and
Orthogonal Fourier-Mellin moments are some methods for feature
extraction of an object.
In this project, Hu moments are used to extract the features of the
Objects. After calculating 6 features from Hu moments, thay are
grouped as three ones in two groups to show 6 dimensional space as
three dimensioned two spaces in the figures given below.

23.

Image Processing via Classical Moments
4. Object Recognition
Object Recognition process can be defined as labeling the
objects which are modelled before.
In this project, 14 object classes are used as seen in the
figure.

24. A Robot Arm with Five Degree of Freedom

Robot Arm System and Control
A Robot Arm with Five Degree of Freedom
Motor # 4
Link # 4
Link # 3 Motor # 3
Motor # 5
Motor # 2
Link # 2
Gripper
Link # 1
Motor # 1

25. The body and the joints of the manipulator are all made from aluminium due to light weight and toughness of this material. For reducing the speed and also to increase the torques of the motors to desirable level, gear reduction mechanisms have been used f

Robot Arm System and Control
The body and the joints of the manipulator are all made from
aluminium due to light weight and toughness of this material. For
reducing
the
speed
and
also
to
increase
the
torques of the motors to desirable level, gear reduction mechanisms
have been used for the actuators of the joints.
First, kinematic analysis and “link table “ of the revolute jointed
manipulator with five degrees of freedom is investigated.
Furthermore, a path following and control algorithm software for
joint motors is developed to move the manipulator through a given
trajectory.

26. Coordinates Located into the links

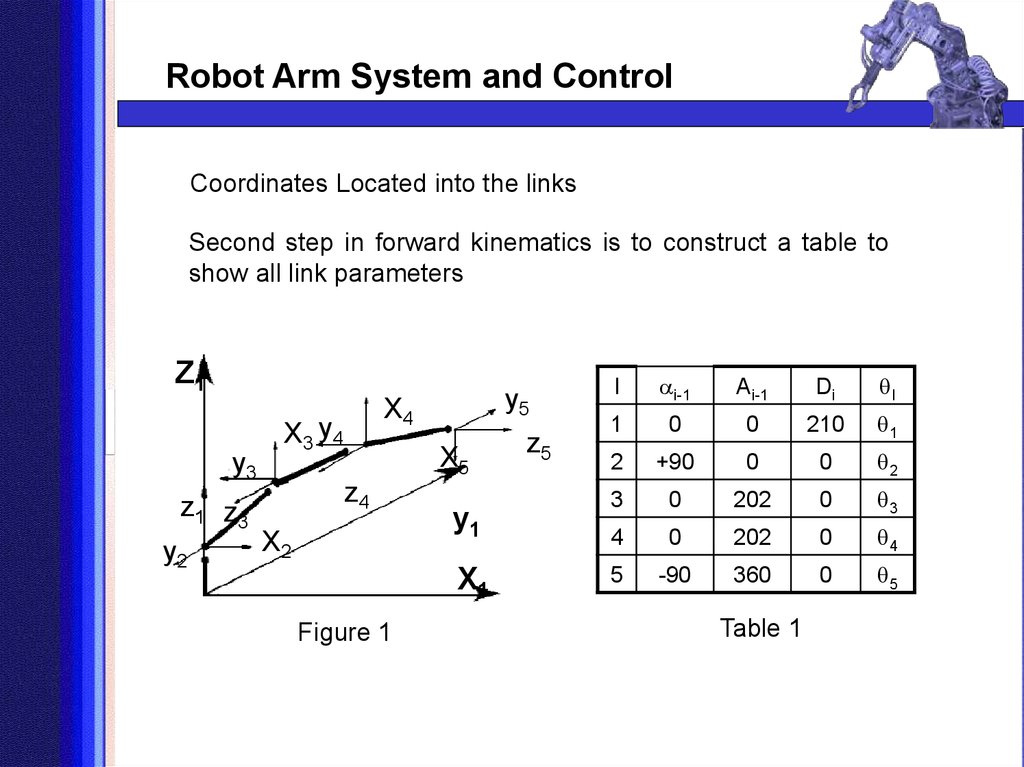
Robot Arm System and Control
Coordinates Located into the links
Second step in forward kinematics is to construct a table to
show all link parameters
Z1
y3
z1 z3
y2
y5
X4
X3 y4
X5
z4
X2
y1
X1
Figure 1
z5
I
i-1
Ai-1
Di
I
1
0
0
210
1
2
+90
0
0
2
3
0
202
0
3
4
0
202
0
4
5
-90
360
0
5
Table 1

27. Transformation matrices according to table are,

Robot Arm System and Control
Transformation matrices according to table are,
c1
s
0
1
1T
0
0
s1
c1
0
c 3
s
2
3
3T
0
0
s3
c3
0
0
0
0 0
0 0
1 210
0 1
c2
0
1
2T
s 2
0
0 202
0 0
1 0
0 1
c 4
s
3
4
4T
0
0
c5
0
4
5T
s5
0
s5
0
c5
0
s 21 0 0
0
1 0
c 2 0 0
0
0 1
s4
c4
0
0
0 360
1 0
0 0
0 1
0 202
0 0
1 0
0 1

28.

Robot Arm System and Control
In deriving the kinematical equations, we formed the product of
link transformations:
Forming the product to obtain;
T 01T.21T.23T.43 T.45T
0
5
r11
r
5
21
0T
r3"
0
r12
r13
r22
r32
r23
r33
0
0
Px
Py
Pz
1

29. Px , Py, Pz, can be found with respect to the angles θ1,2,3,4

Robot Arm System and Control
Px , Py, Pz, can be found with respect to the angles θ1,2,3,4
After finding the solution matrices, program executes for choosing
the best solution for the manipulator control. The criteria of
choosing the best one are, searching the easiest and shortest
movement of the manipulator.
In this study, the aim is obtaining a path control algorithm by using
inverse kinematics method. As told before, by this method
manipulator’s joints angles are determined from the required target
given in Cartesian coordinates. And after these steps the main
control program starts to execute by using joint base control
algorithms.

30. Before the path control applications, the position following capability of the manipulator is tested for each arm. First of all, reconsidering the mechanical design and its workspace; the possible motion capabilities of the manipulator are investigated. J

Robot Arm System and Control
Before the path control applications, the position following
capability of the manipulator is tested for each arm. First of all,
reconsidering the mechanical design and its workspace; the
possible motion capabilities of the manipulator are investigated.
Joint based control is used for each joint by applying additional
control algorithms. Responses of the joints for different control
algorithms are tested.
Figure 2
Figure 3

31.

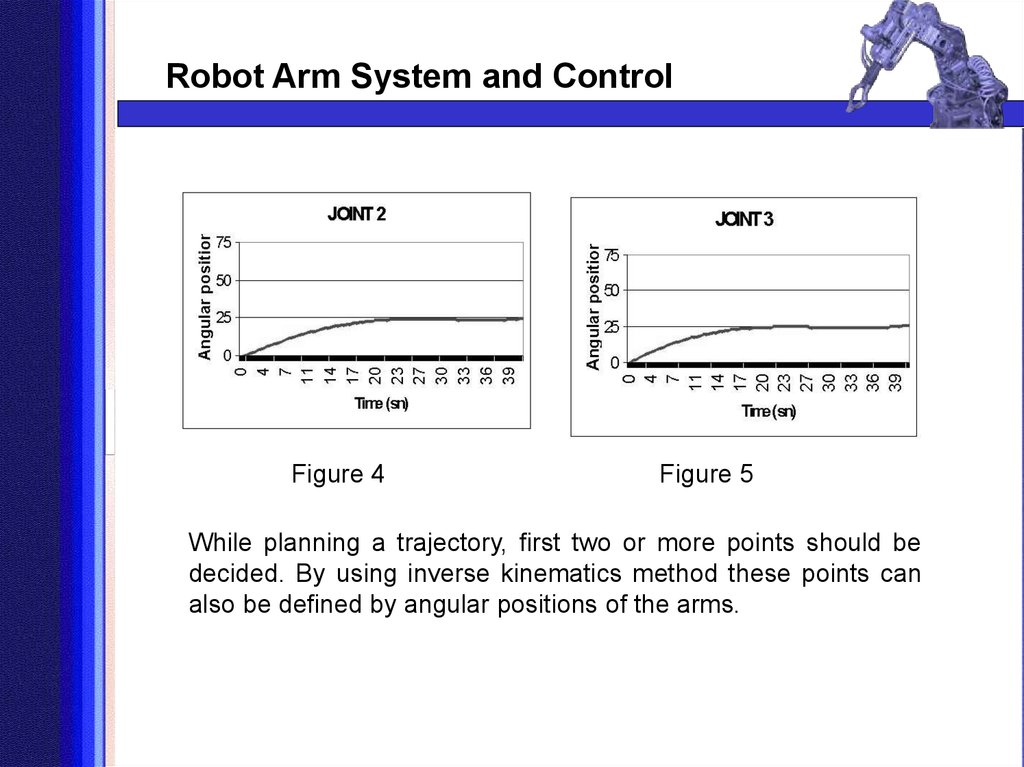
Robot Arm System and Control
Figure 4
Figure 5
While planning a trajectory, first two or more points should be
decided. By using inverse kinematics method these points can
also be defined by angular positions of the arms.

32.

Robot Arm System and Control
After defining these angles, the trajectory of a joint can be
described by a polynomial equation as given below.
Θ(t)=a0 + a1 t + a2 t2 + a3 t3
and the angular velocity can be defined as,
.
Θ’(t)= a1 + 2 a2 t + 3 a3 t2
If the coefficients can be determined correctly then the trajectory
following will be possible.
After determining these coefficients, we can generate the control
algorithm of the manipulator by applying the time depended
angular velocity equation.

33.

Robot Arm System and Control
As an example the trajectory and parameters of the manipulator
are given in table below:
.
J0
J1
J2
J4
θ0=64.6 0
θ0=8.5 0
θ0= -5 0
θ0=57 0
θf=41.1 0
θf=8.8 0
θf=22.8 0
θf=58 0
Dθ=23.5 0
Dθ=-0.3 0
Dθ=27.8 0
Dθ=1 0
Dt=6.77 s
Dt=0.05 s
Dt=9.62 s
Dt=0.27 s
Table 2
Here Dθ represents the amount of the way that the manipulator
takes among this trajectory, and also Dt represents the time that
the joint needs for reaching the end point. Dt can easily be
computed by the division of the (Dθ/ w) where w is in (0/s) format.

34.

Robot Arm System and Control
By this table, we can easily determine the needed time of the arms for
whole trajectory. Since we want all joints to start and end their motions at
the same time then we have to choose each joint a specific time value.
After that, we can determine the angular velocities of the arms by using
the equations which are formed via using Table 2.
.
In this study there are two objects with their own placing points after
picking from the conveyor band. Thus there are two paths determined for
the manipulator and the path following features are observed for each of
them. Results can be seen in figures below.
Figure 6 Path for object A
(in XY plane)
Figure 7 Path for object A
(in XZ plane)

35.

Conclusion
• After theoretical study, to test the performance of the presented
algorithym, an application mechanism is prepared as shown before. During
the tests, system classified 14 predefined objects in 500 times random
taken photos of passing objects. In these tests, the 95% of the system
decisions were right. And it is determined that most of the reasons of the
faults were that the objects were far from the center of the conveyor band.
• Even there are a little data loss for the bigger objects in 14 classes,
identification is realized whereas there were some problems (mentioned in
5% faults) for the smaller objects.
• In addition, when the noise in reduced data of the objects which are
same in color with the conveyor band is homogenous, it doesn’t affect the
identification algorithym; but if the noise is in the characteristic of damaging
the region distrubition of any object, it causes errors for the algorithym.
• Improving the mechanical system of the conveyor system, performance
of the software can be higher. Furthermore, with a conveyor band that has
homogenous reflection coefficient distribution and is not swinging during
moving the percentage of right identification can be improved,

36.

Conclusion
•It is observed that, with its present design, manipulator is more
favourable in pick and place operations. However, by adding a
prismatic joint, manipulator will be more sensitive and smooth for
two-dimensional motions.
•In addition, high reduction usage of the motion motors due to the
limited sources has caused limited velocity adjustments, where it
is necessary for smooth path control of the manipulator. Also the
result of the low speed is observed when joints need high
moments for path control. It is clear that usage of high capacity AC
or DC servo-motors can prevent this problem.
•Again due to limited sources, multi-turn potentiometers are used
for the measurement of the joint angles. And it is observed that the
hysterisys of these potentiometers while the arms moves forward
and backwards affect the smoothness and the repeatability
features of the manipulator in negative way.