Похожие презентации:
Теорема Остроградского – Гаусса. Лекция 2
1. Лекция 2. Теорема Остроградского – Гаусса
20132.
Историческая справкаТеорема Остроградского - Гаусса – основная теорема
электродинамики; применяется для расчета электрических
полей; входит в систему уравнений Максвелла.
1826 г. – акад. М.В. Остроградский, вывел
общую формулу, связанную с
преобразованием объемного интеграла
к поверхностному.
1844 г. – К.Ф. Гаусс, установил взаимосвязь
потока вектора напряженности
электрического поля с зарядом в объеме,
ограниченным этой поверхностью.
3
3.
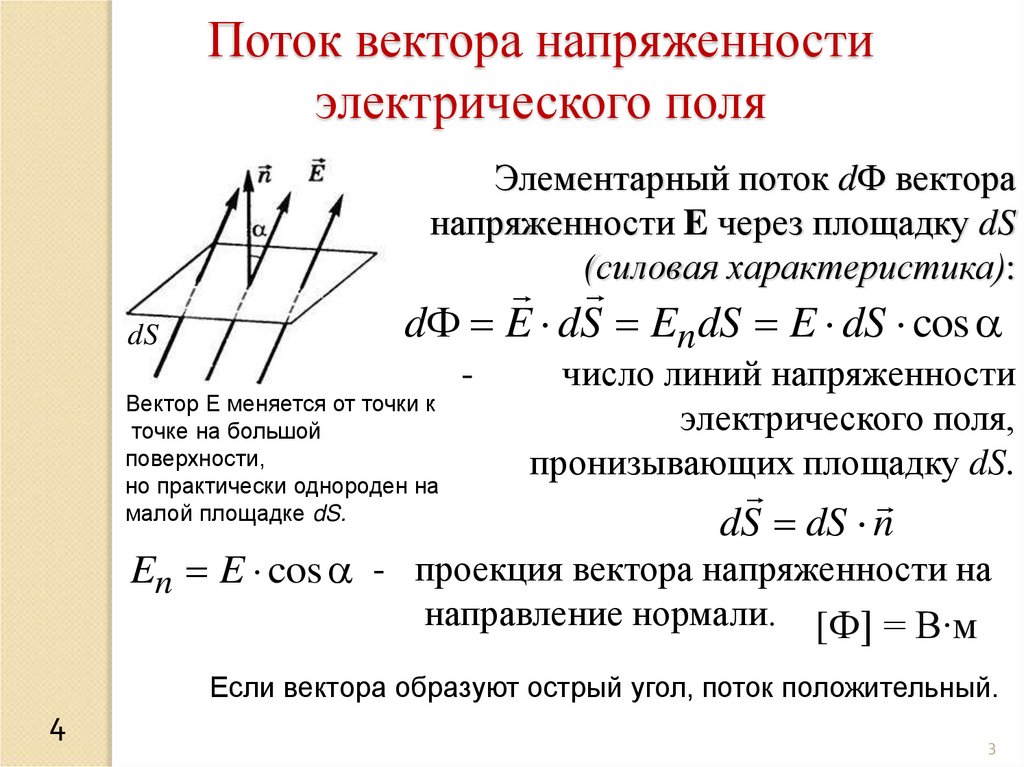
Поток вектора напряженностиэлектрического поля
Элементарный поток dФ вектора
напряженности E через площадку dS
(силовая характеристика):
dS
d E dS En dS E dS cos
Вектор Е меняется от точки к
точке на большой
поверхности,
но практически однороден на
малой площадке dS.
-
число линий напряженности
электрического поля,
пронизывающих площадку dS.
dS dS n
En E cos - проекция вектора напряженности на
направление нормали. [Ф] = B∙м
Если вектора образуют острый угол, поток положительный.
4
3
4.
Поток вектора напряженностичерез произвольную поверхность:
Ф d EdS EndS
S
S
S
через замкнутую поверхность:
Ф d EdS EndS
S
S
S
однородного поля (E=const) через поверхность S
Ф E S En S E S cos
α – угол между нормалью к поверхности и линиями
напряженности электрического поля.
5
4
5.
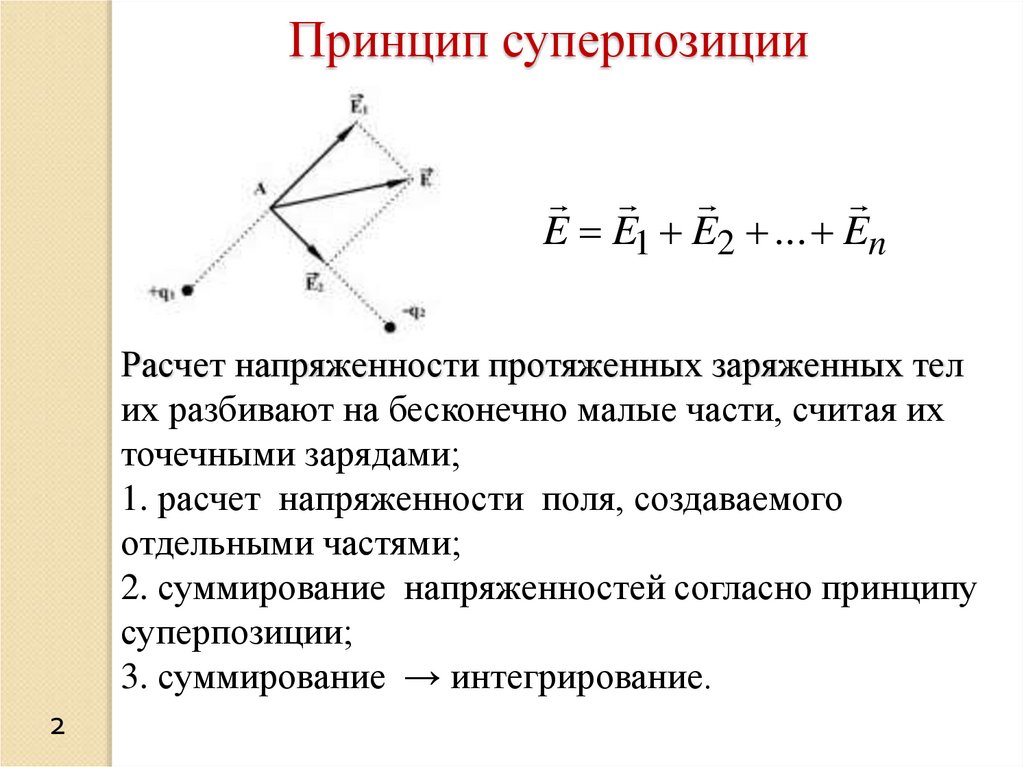
Принцип суперпозицииE E1 E2 ... En
Расчет напряженности протяженных заряженных тел
их разбивают на бесконечно малые части, считая их
точечными зарядами;
1. расчет напряженности поля, создаваемого
отдельными частями;
2. суммирование напряженностей согласно принципу
суперпозиции;
3. суммирование → интегрирование.
2
6.
Теорема Гаусса (1844)Полный поток вектора напряженности E через замкнутую
поверхность равен алгебраической сумме всех зарядов,
заключенных внутри этой поверхности, деленной на ε0.
1
EdS qвнутр
0
S
ε0 - диэлектрическая проницаемость вакуума
Поток напряженности поля Е через любую замкнутую
поверхность, внутри которой полный заряд равен нулю,
также равен нулю.
6
6
7.
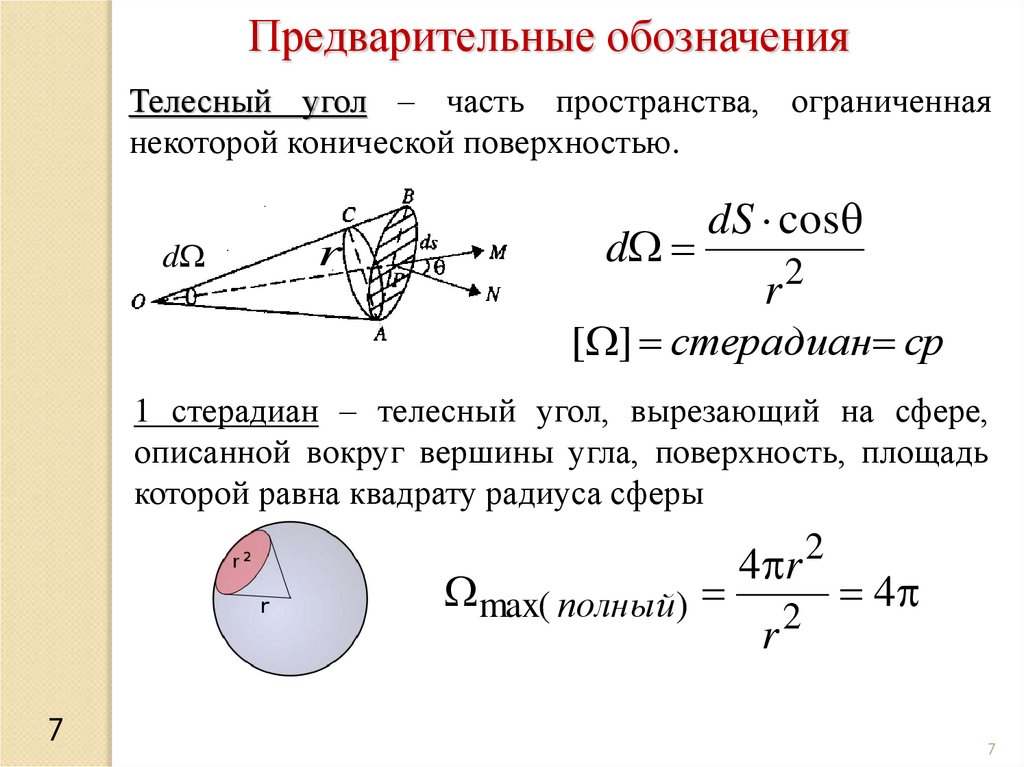
Предварительные обозначенияТелесный угол – часть пространства, ограниченная
некоторой конической поверхностью.
d
r
d
dS cos
r2
[ ] стерадиан ср
1 стерадиан – телесный угол, вырезающий на сфере,
описанной вокруг вершины угла, поверхность, площадь
которой равна квадрату радиуса сферы
max( полный )
7
4 r 2
r2
4
7
8.
Доказательство теоремы Гаусса1
q
4 0 r 2
1
q
q
d EdS
dS cos
d
2
4 0 r
4 0
Напряженность поля точечного заряда: E
q
q
d
d
4 0 S
0
S
С точки зрения физики, теорема Гаусса и закон Кулона
эквиваленты, это один и тот же физический закон, облаченный в
разные математические оболочки.
Непрерывное распределение заряда:
8
q
1
EdS dV
0
0V
S
ρ – объемная плотность
распределения заряда.
8
9.
Применение теоремы ГауссаПрименяется для расчета электрических полей в задачах со
специальной симметрией.
1. Напряженность электрического поля бесконечной равномерно
заряженной плоскости с поверхностной плотностью заряда σ:
E
2 0
Поле однородно (в каждой точке поля
E=const)
2. Напряженность поля двух бесконечных равномерно заряженных
разноименными зарядами параллельных плоскостей:
напряженности полей обеих плоскостей между плоскостями
направлены в одну сторону, сл-но, их геометрическая сумма явл. их
арифметической суммой в вакууме:
9
9
10.
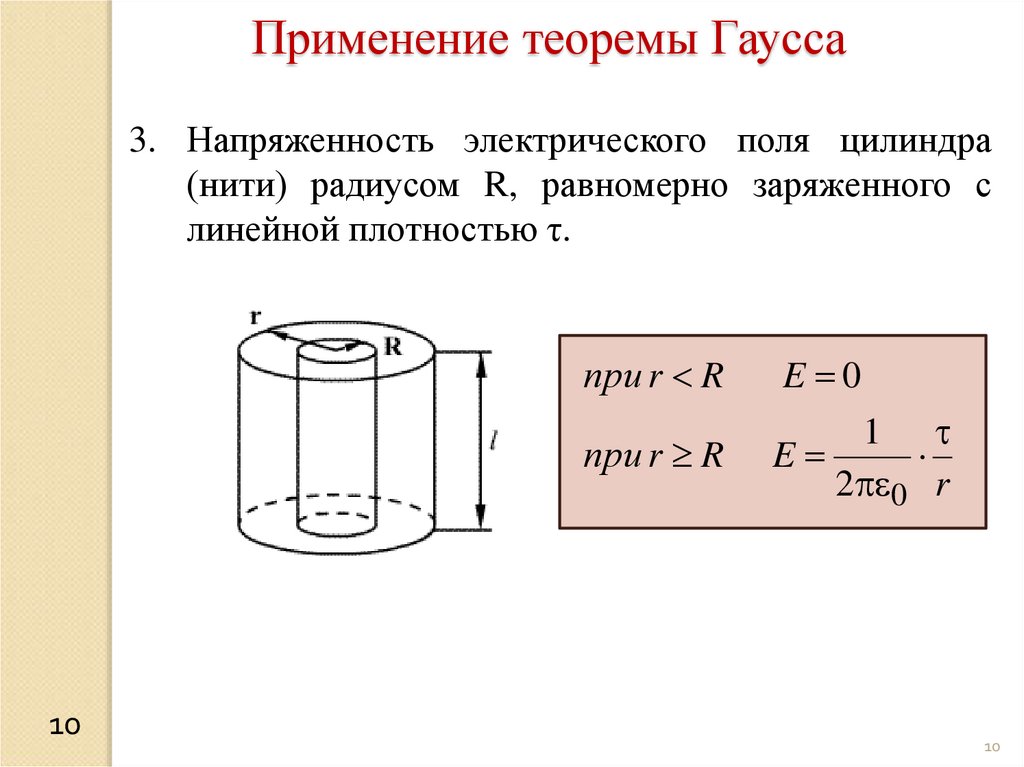
Применение теоремы Гаусса3. Напряженность электрического поля цилиндра
(нити) радиусом R, равномерно заряженного с
линейной плотностью τ.
10
при r R
E 0
при r R
1
E
2 0 r
10
11.
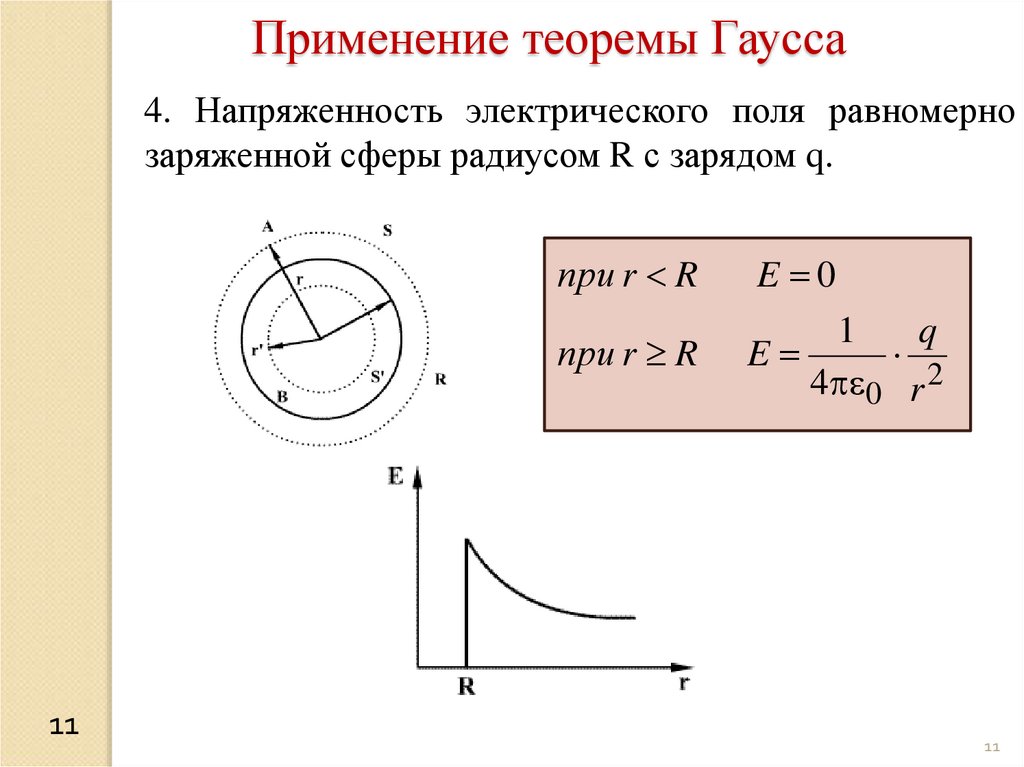
Применение теоремы Гаусса4. Напряженность электрического поля равномерно
заряженной сферы радиусом R с зарядом q.
11
при r R
E 0
при r R
1
q
E
4 0 r 2
11
12.
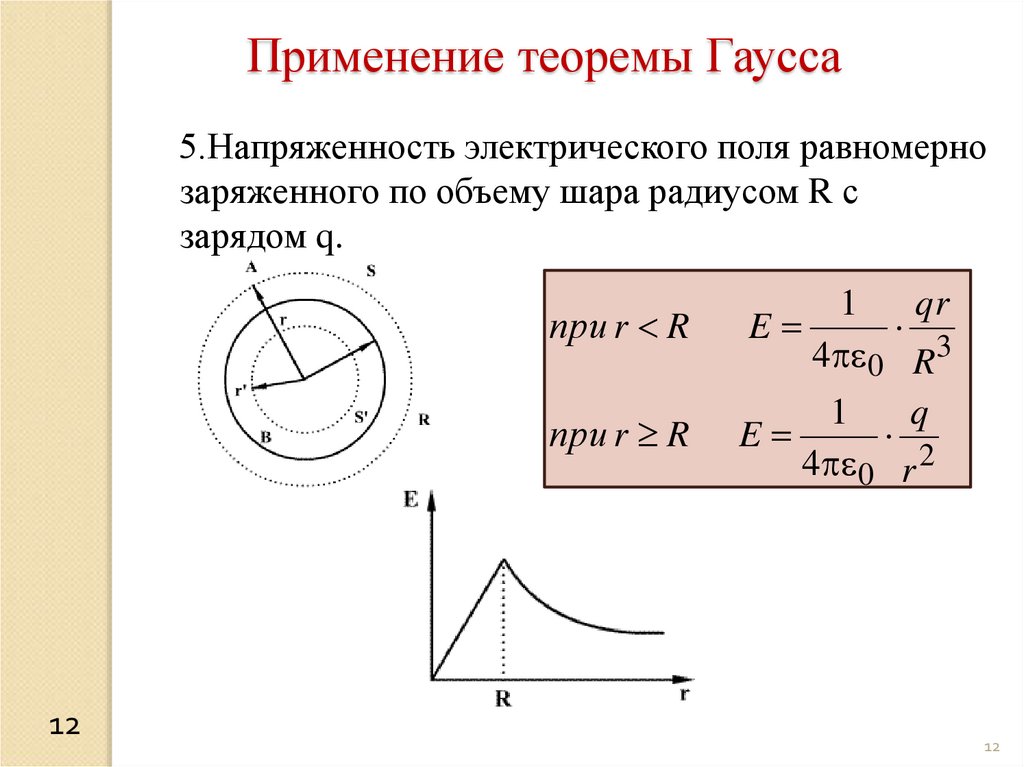
Применение теоремы Гаусса5.Напряженность электрического поля равномерно
заряженного по объему шара радиусом R с
зарядом q.
12
при r R
1
qr
E
4 0 R3
при r R
1
q
E
4 0 r 2
12
13.
Теорема Гаусса в дифференциальной формеТеорема Гаусса в интегральной форме:
q
1
1
EdS dV V
0
0V
0
S
или
1 1
EdS
VS
0
V→0 (плотность в объеме можно считать постоянной)
1 1
lim EdS
0
V 0 V S
1 - дивергенция
divE lim EdS
V 0 V S
операция дифференцирования, в результате применения
которой к векторному полю получается скалярное поле
13
13
14.
Теорема Гаусса в дифференциальной формеДивергенция векторного поля в декартовых координатах:
E x E y E z
divE
x
y
z
Дивергенция — это линейный дифференциальный оператор на
векторном поле, характеризующий поток данного поля через
поверхность малой окрестности каждой внутренней точки
области определения поля.
Векторный дифференциальный оператор
прямоугольных декартовых координатах:
i
j k
x
y
z
Теорема Гаусса в дифференциальной форме:
divE E
0
14
набла
в
насколько расходится входящее и
исходящее из малой окрестности
данной точки поле напряженности
14
15.
Теорема ГауссаВ дифференциальной форме она является локальной
теоремой, связывающей объемную плотность заряда ρ и
divE в одной и той же точке поля. Во всех точках поля, где
divЕ>0 имеются источники поля – положительные заряды,
а где divЕ<0, находятся отрицательные заряды – стоки
поля, а где divE=0, силовые линии проходят, но не
рождаются и не исчезают (зарядов нет).
divE E
0
15
Теорема Гаусса в интегральной форме устанавливает
связь между физическими величинами в сколь угодно
далеких точках пространства в один и тот же момент
времени.
q
1
EdS dV ρ – объемная плотность
S
0
0V
распределения заряда.
15








 Физика
Физика








