Похожие презентации:
Метод расчёта электрических полей на основе теоремы Гаусса. Тема 3
1. Омский государственный технический университет Кафедра физики
Калистратова Л.Ф.Электронные лекции по разделам
электромагнетизма
(электростатика, постоянный ток, магнетизм)
17 лекций
(34 аудиторных часа)
2. Тема 3. Метод расчёта электрических полей на основе теоремы Гаусса
План лекции1. Электрическое поле заряженной нити.
2. Электрическое поле заряженной плоскости.
3. Электрическое поле плоского конденсатора.
4. Электрическое поле заряженной сферы.
5. Электрическое поле заряженного шара.
3. 1. Электрическое поле заряженной нити
Пусть бесконечная нить однородно заряжена слинейной плотностью заряда.
dq
dl
E=?
r
Будем считать заряд нити
положительным по знаку.
Вычислим напряженность поля Е
на расстоянии r от нити.
+q
4.
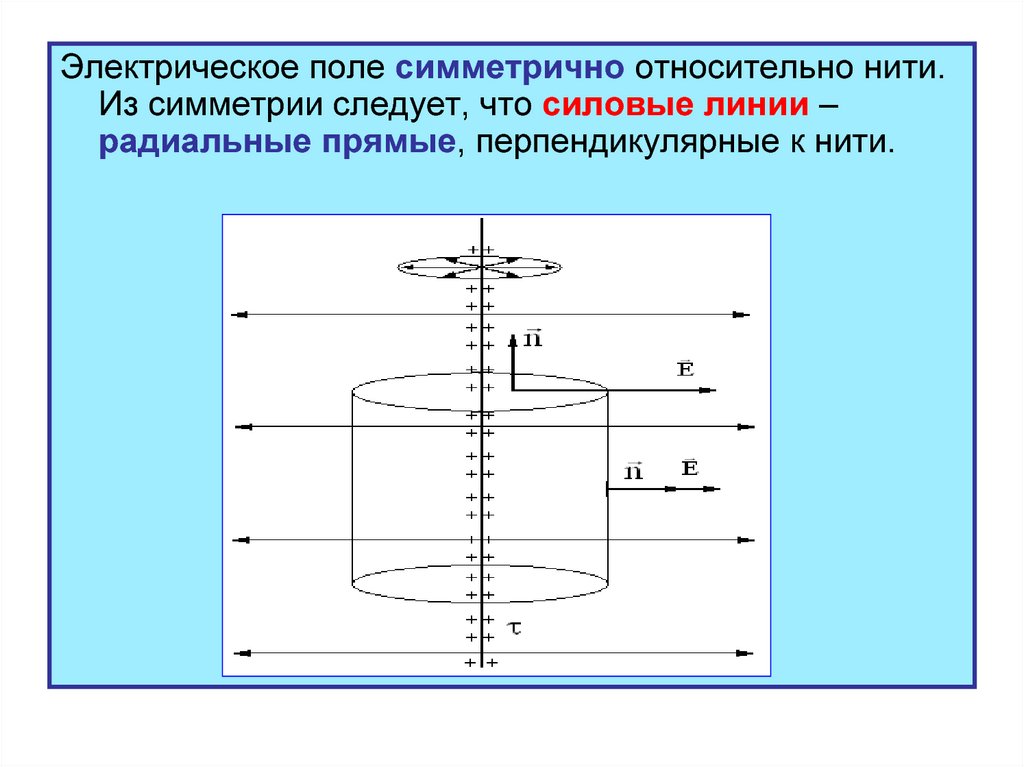
Электрическое поле симметрично относительно нити.Из симметрии следует, что силовые линии –
радиальные прямые, перпендикулярные к нити.
5.
В качестве гауссовой поверхности следует выбратьзамкнутую цилиндрическую поверхность радиусом
r и высотой h, коаксиальную с нитью.
r
h
6.
Поток вектора E через эту цилиндрическуюповерхность складывается из потока через боковую
поверхность и потоков через два основания
цилиндра:
N EdS E n dS
S
Sбок.
E
dS
n
Sверх. осн
E
dS
.
n
Sниж. осн.
Второй и третий интегралы (потоки напряжённости
через основания) равны нулю, так как эти основания
параллельны линиям :
E
E n dS 0
осн.
На боковой же поверхности цилиндра E
׀׀dS .
7.
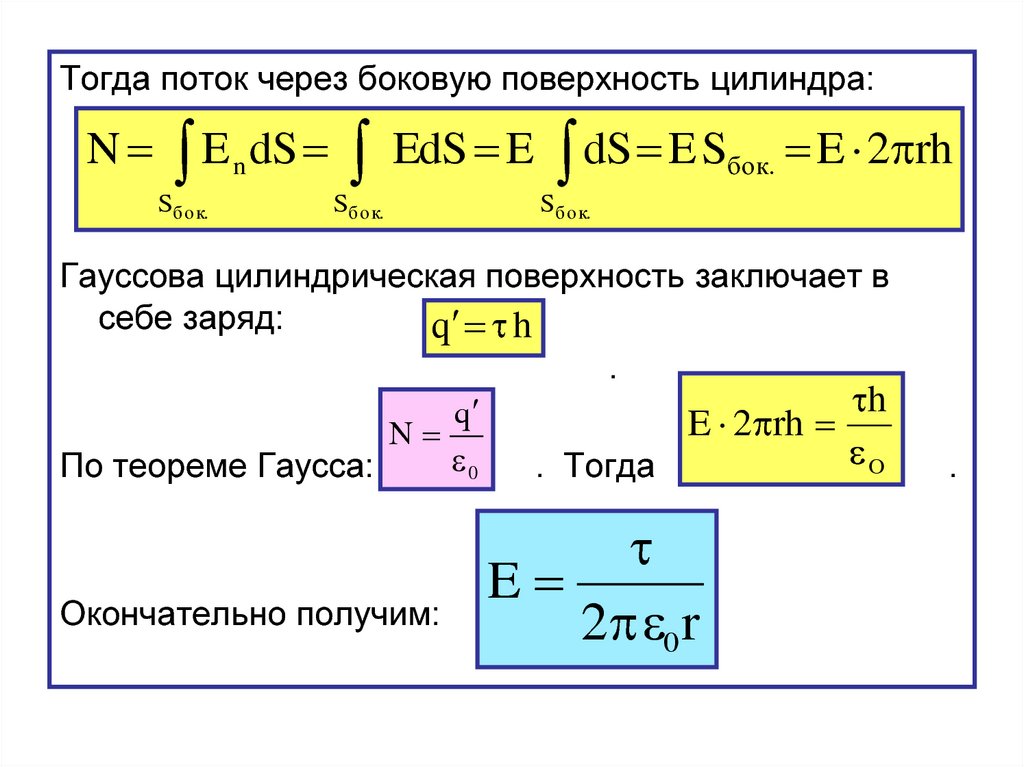
Тогда поток через боковую поверхность цилиндра:N
E dS
n
Sбок.
EdS E
Sбок.
dS E S
бок.
E 2 rh
Sбок.
Гауссова цилиндрическая поверхность заключает в
себе заряд:
q h
.
h
q
E 2 rh
N
O
0
По теореме Гаусса:
. Тогда
Окончательно получим:
E
2 0 r
.
8.
Напряженность полянити:
- прямо
пропорциональна
линейной плотности
заряда;
- обратно
пропорциональна
расстоянию от нити.
2k
E
2 0 r
r
Е
9.
Для вычисления потенциала используем формулусвязи напряженности и потенциала:
d Er dr
Проинтегрируем
2
r2
d E
1
обе части выражения:
r
dr
r1
2k
E
r
Проведем интегрирование, подставив в последнее
выражение формулу напряжённости.
2k
r1
2 1
dr 2k ln
r
r2
r1
r2
10.
Конкретную зависимость потенциала от расстоянияполучим, если примем,
что при r1 0 потенциал равен 1 0
,
а при
r2 r
потенциал равен 2 r .
Тогда можно записать
r 0 2k ln r
Потенциал убывает с увеличением расстояния по
закону натурального логарифма от максимального
значения 0 до нуля.
11. 2. Электрическое поле заряженной плоскости
Пусть бесконечная плоскость равномерно заряжена споверхностной плотностью заряда + :
dq
dS
+
r
Вычислим напряжённость поля
на расстоянии r от плоскости.
E = const
12.
Cиловые линии в обе стороны параллельны междусобой и перпендикулярны плоскости.
Напряжённость поля в точках, расположенных по обе
стороны от плоскости на одинаковых расстояниях:
- равна по величине;
- противоположна по направлению.
Гауссовой поверхностью является поверхность
цилиндра, образующие которого параллельны
линиям поля, а основания S расположены на
одинаковых расстояниях r от плоскости.
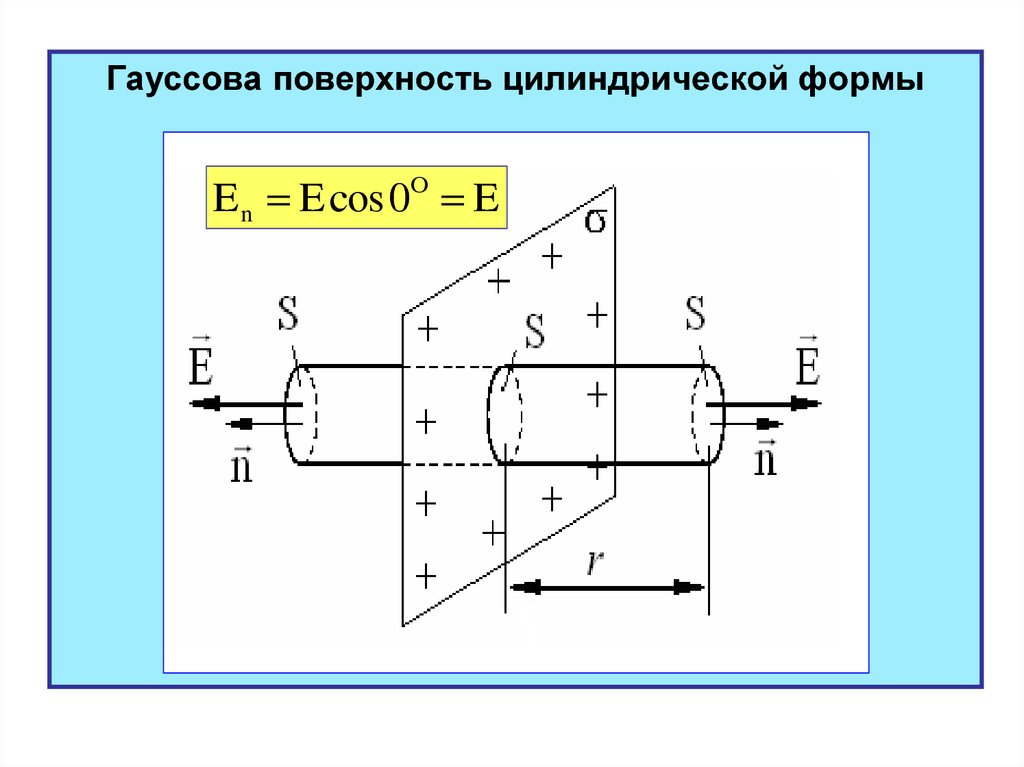
13.
Гауссова поверхность цилиндрической формыE n E cos 0O E
14.
Полный поток линий E через эту поверхностьскладывается из потоков через основания цилиндра
и его боковую поверхность:
N
E dS 2 E dS E dS 2ES
n
цил.
пов.
n
осн.
n
осн.
бок.
пов.
Поток через боковую поверхность равен нулю, так
как вектор напряжённости параллелен этой
поверхности.
Поток вектора напряжённости через два основания:
N 2 ESосн
15.
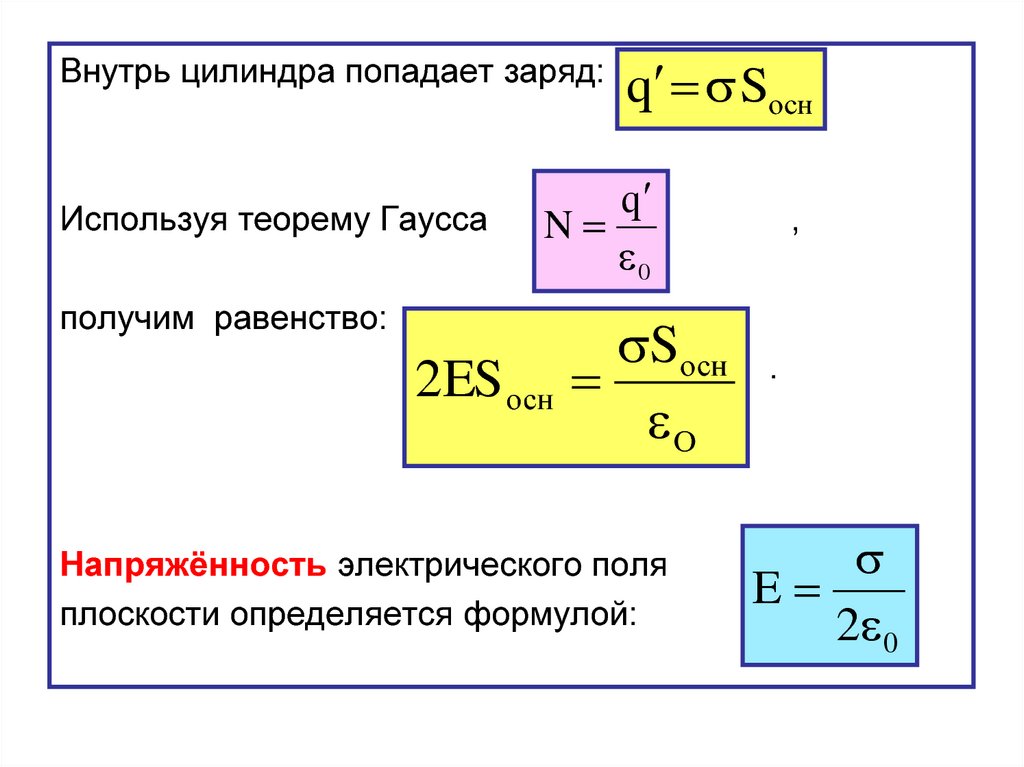
Внутрь цилиндра попадает заряд:Используя теорему Гаусса
.
q Sосн
q
N
0
получим равенство:
2ES осн
Sосн
O
Напряжённость электрического поля
плоскости определяется формулой:
,
.
E
2 0
16.
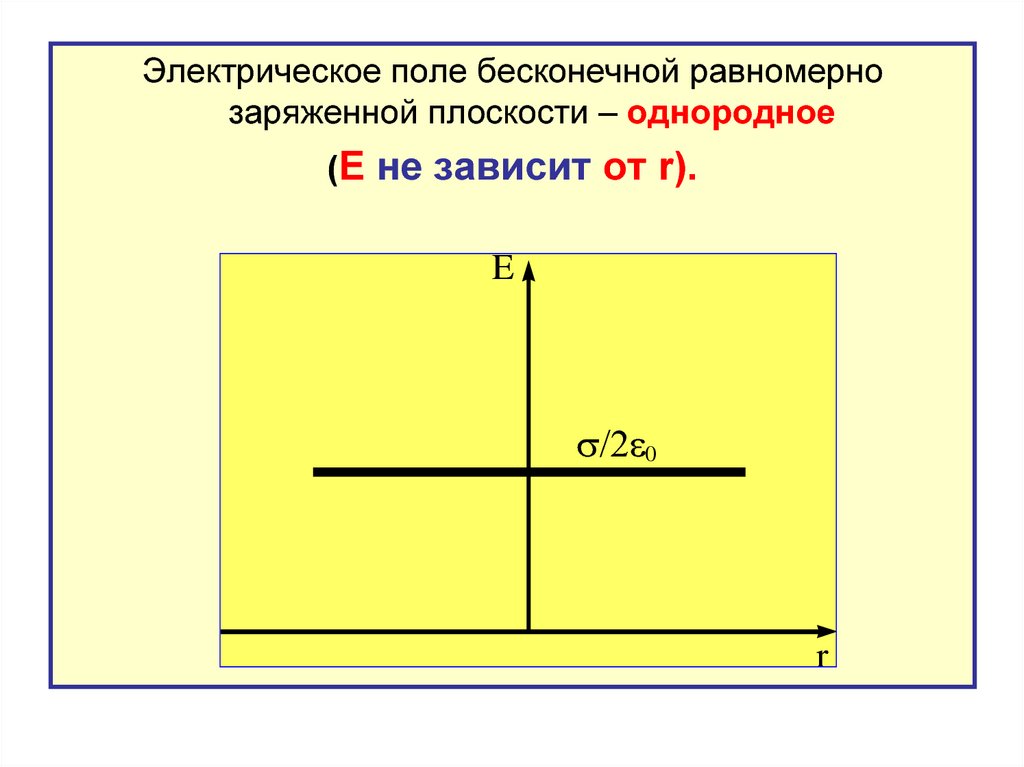
Электрическое поле бесконечной равномернозаряженной плоскости – однородное
(E не зависит от r).
E
0
r
17.
Определим разность потенциалов двух точек,расположенных на одной силовой линии.
+
1
2
r1
r2
Запишем формулу связи потенциала с
напряжённостью:
d Edr
E
2 0
Подставим формулу напряжённости и проинтегрируем
полученное выражение.
18.
Тогда2
d r 2 0 dr
1
1
r2
или
r1 r2
2 1
2 0
Примем, что при r1 0 потенциал равен
и при r r потенциал равен
2 r
2
Тогда
1 0
0 r
r 0
2 0
r
r 0
2 0
19.
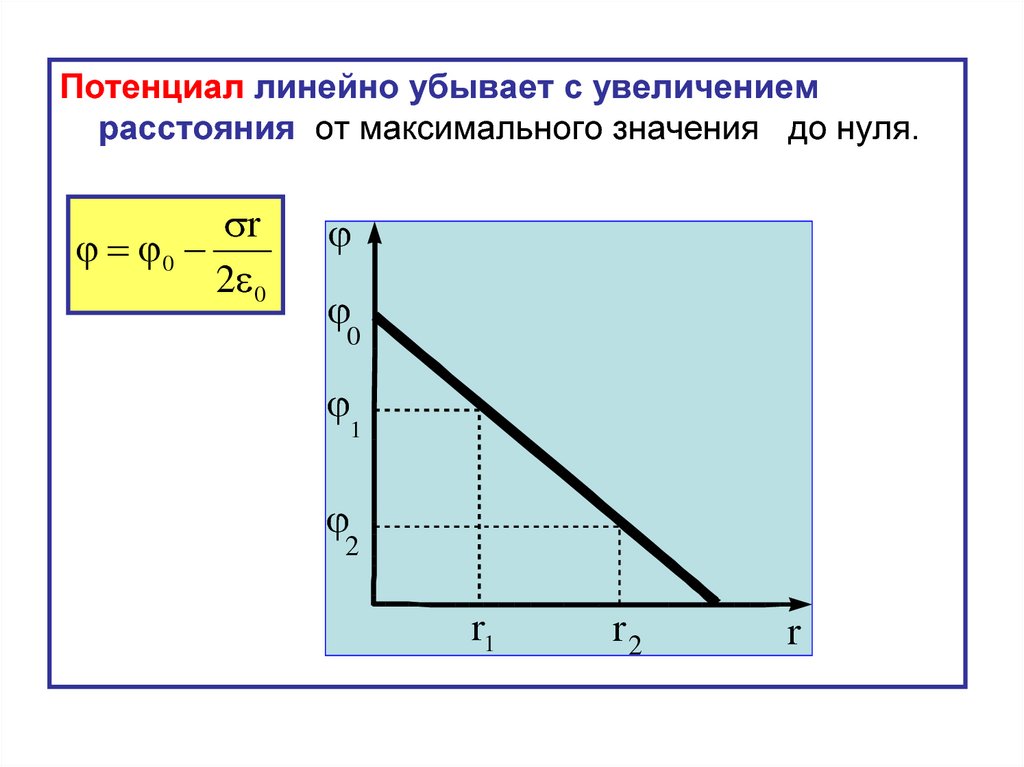
Потенциал линейно убывает с увеличениемрасстояния от максимального значения до нуля.
r
0
2 0
0
1
2
r1
r2
r
20. 3. Электрическое поле плоского конденсатора
Плоским конденсатором называется система двухзаряженных металлических плоскостей
(пластин), находящихся на расстоянии d друг от
друга.
Плоскости заряжены разным по знаку, но одинаковым
по величине зарядом q = S, где S – площадь
пластин.
Между пластинами может быть помещён диэлектрик с
диэлектрической проницаемостью .
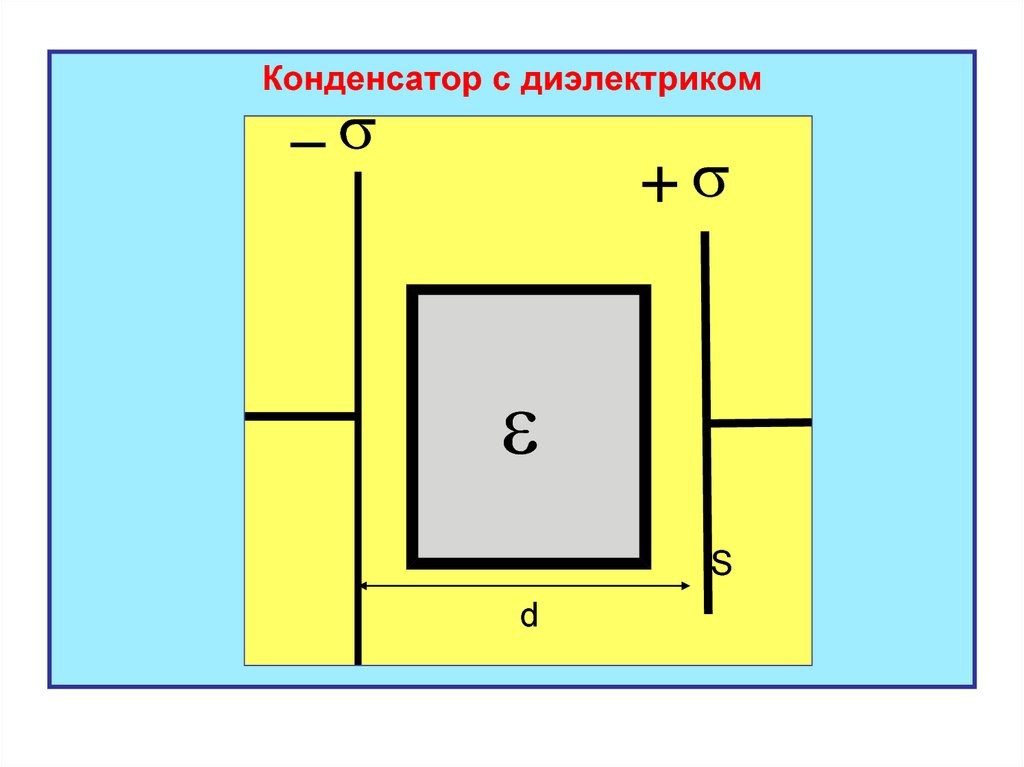
21.
Конденсатор с диэлектрикомS
d
22.
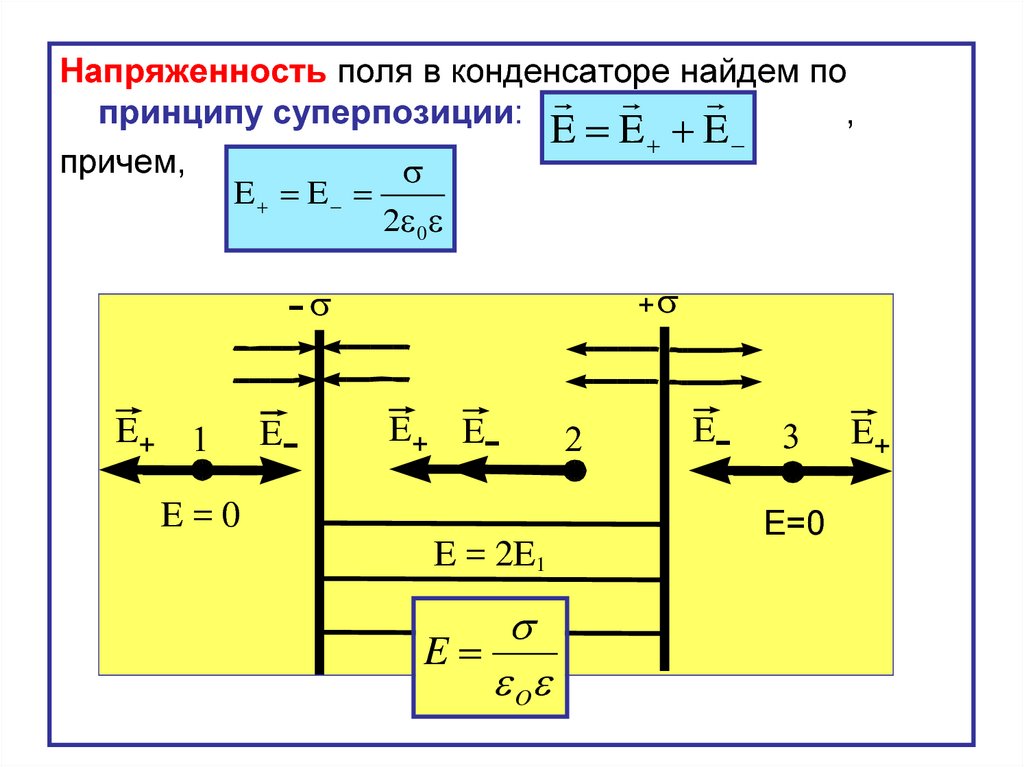
Напряженность поля в конденсаторе найдем попринципу суперпозиции:
,
E E E
причем,
E E
2 0
+
-
E+
E-
E+ E-
E=0
E = 2E1
E
O
E-
Е=0
E+
23.
Напряжённость поля в конденсаторе с диэлектриком:E
0
Электрическое поле в плоском конденсаторе с
бесконечными пластинами – однородное.
24.
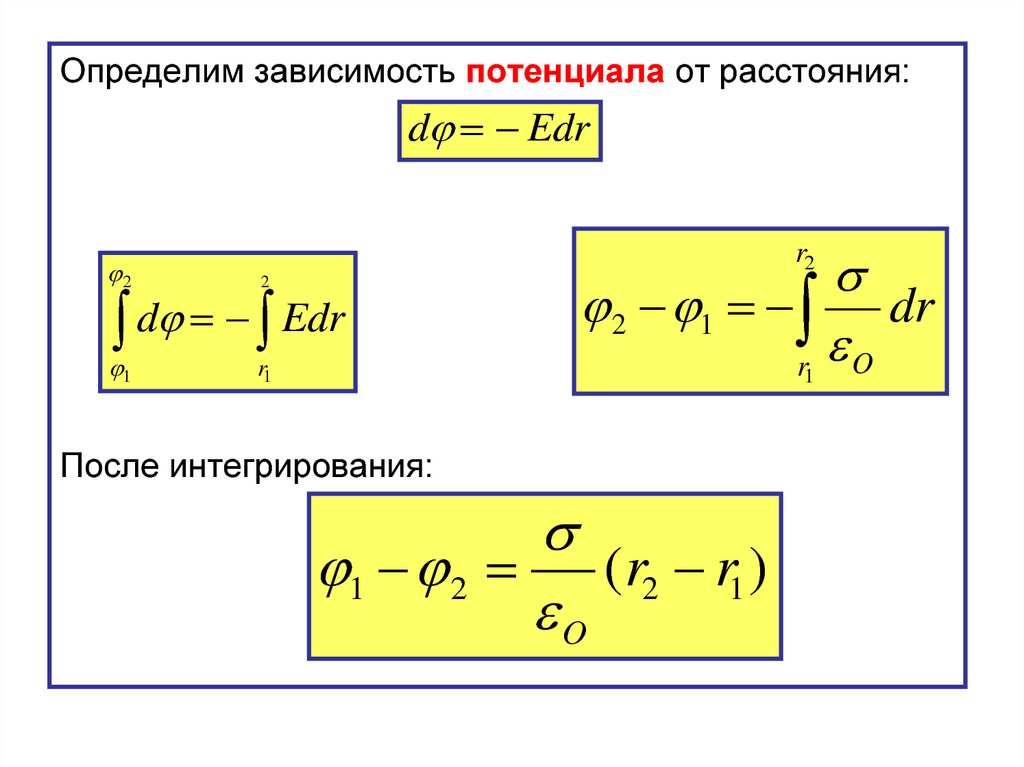
Определим зависимость потенциала от расстояния:d Edr
2 1 dr
O
r
r2
2
2
1
r1
d Edr
После интегрирования:
1 2 (r2 r1 )
O
1
25.
Примем, что прии при r2 d
Получим
Окончательно
r1 0 потенциал равен O
потенциал равен
d
d O
d
0
d O
d
0
Потенциал линейно уменьшается от одной пластины
конденсатора к другой.
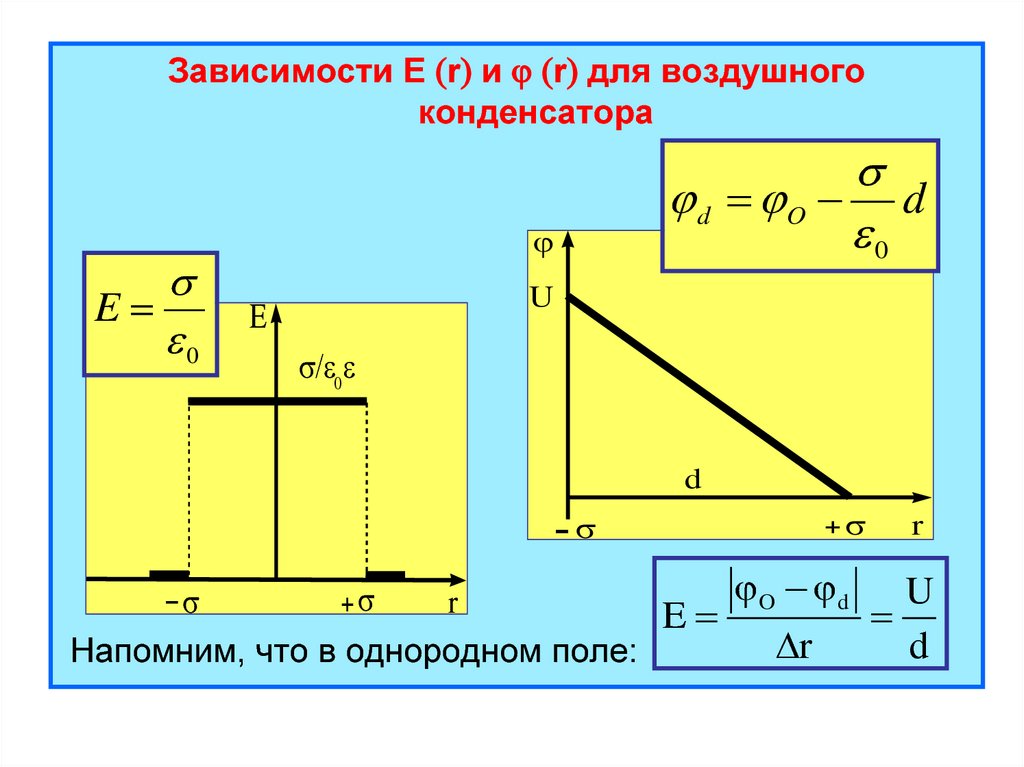
26.
Зависимости E r и r для воздушногоконденсатора
E
0
d O d
0
U
E
0
d
-
+
r
O d U
r
E
r
d
Напомним, что в однородном поле:
_
+
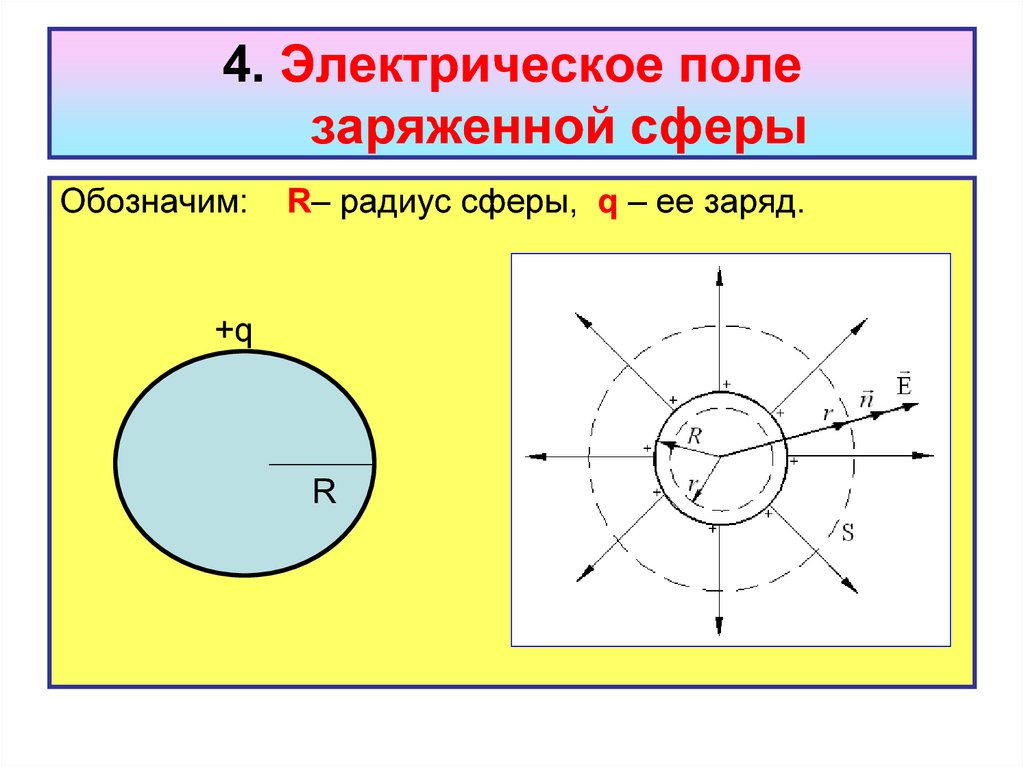
27. 4. Электрическое поле заряженной сферы
Обозначим:R– радиус сферы, q – ее заряд.
+q
R
28.
Заряды расположены на поверхности сферы, причём2
q S 4 R
σ - поверхностная плотность заряда/
q
R
n
E
29.
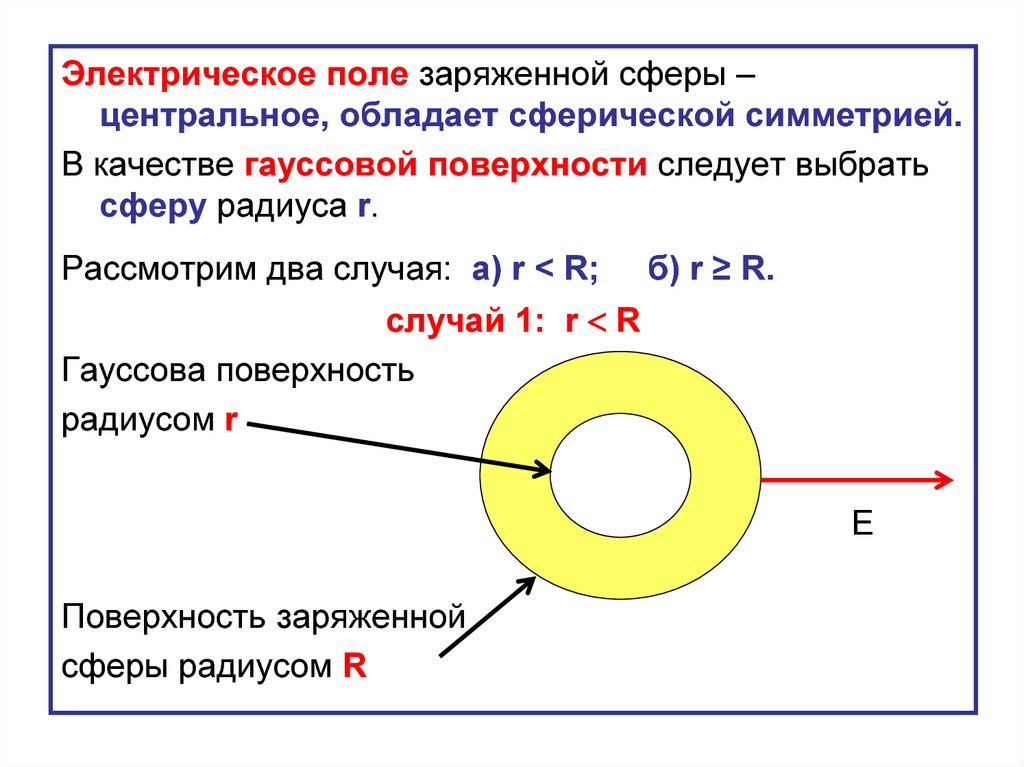
Электрическое поле заряженной сферы –центральное, обладает сферической симметрией.
В качестве гауссовой поверхности следует выбрать
сферу радиуса r.
Рассмотрим два случая: а) r < R;
б) r ≥ R.
случай 1: r R
Гауссова поверхность
радиусом r
Е
Поверхность заряженной
cферы радиусом R
30.
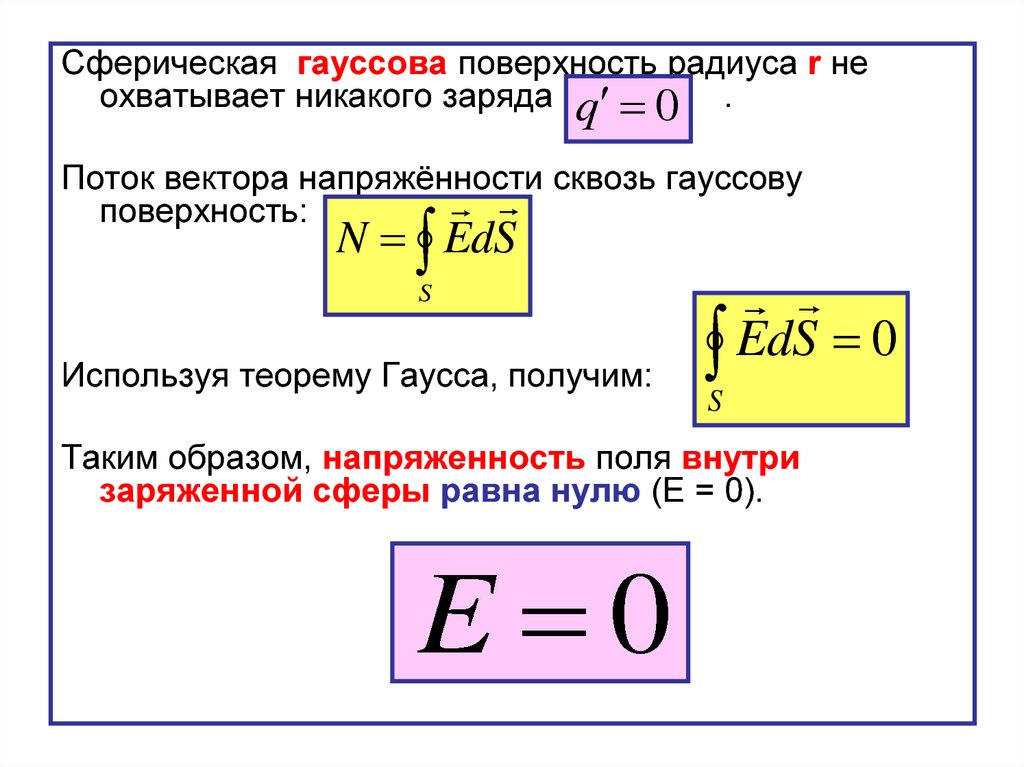
Сферическая гауссова поверхность радиуса r неохватывает никакого заряда q 0 .
Поток вектора напряжённости сквозь гауссову
поверхность:
N EdS
S
Используя теорему Гаусса, получим:
EdS 0
S
Таким образом, напряженность поля внутри
заряженной сферы равна нулю (Е = 0).
E 0
31.
Случай 2: r ≥ RТак как E ║ n во всех точках гауссовой поверхности,
то поток силовых линий через гауссову поверхность
радиуса r равен:
N E dS E n dS E dS ES E 4 r 2
S
S
S
Гауссова поверхность
E
Поверхность сферы
q
n
E
E n E cos 0O E
32.
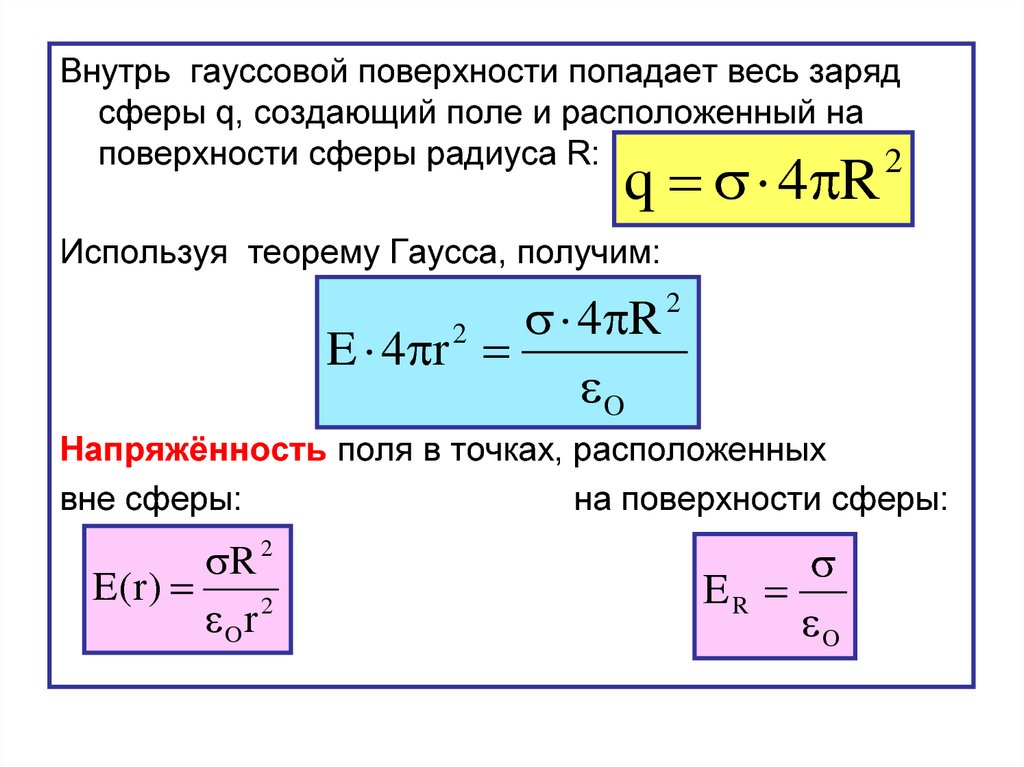
Внутрь гауссовой поверхности попадает весь зарядсферы q, создающий поле и расположенный на
поверхности сферы радиуса R:
2
q 4 R
Используя теорему Гаусса, получим:
4 R
E 4 r
O
2
2
Напряжённость поля в точках, расположенных
вне сферы:
на поверхности сферы:
R 2
E(r )
O r 2
ER
O
33.
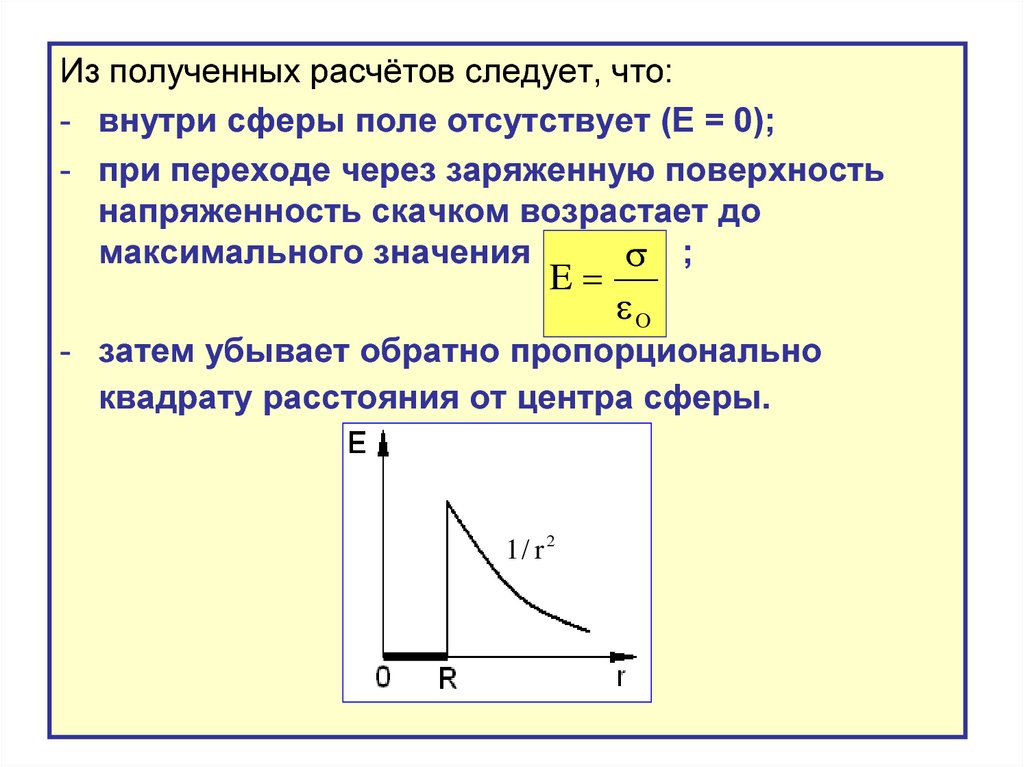
Из полученных расчётов следует, что:- внутри сферы поле отсутствует (Е = 0);
- при переходе через заряженную поверхность
напряженность скачком возрастает до
максимального значения
;
E
O
- затем убывает обратно пропорционально
квадрату расстояния от центра сферы.
1/ r 2
34.
Вычислим потенциал:d E r dr
Для области (r R) можно записать:
r E r dr
r
Потенциал в бесконечности = 0.
R 2
E(r )
O r 2
Тогда с использованием формулы
получим
R
R
r
dr
2
r
O r
r O
2
2
35.
Потенциал на поверхности заряженной сферы (призначении r = R) равен значению
R
R
O
Для точек, лежащих внутри сферы (область: r R)
можно записать
r
r R E r dr
R
Но так как напряжённость Е = 0, то
r R
.
36.
Потенциал:- внутри сферы не зависит от расстояния и равен
значению потенциала на его поверхности;
R
R
const
O
- затем убывает обратно пропорционально
расстоянию от центра сферы.
R
const
1/r
R
r
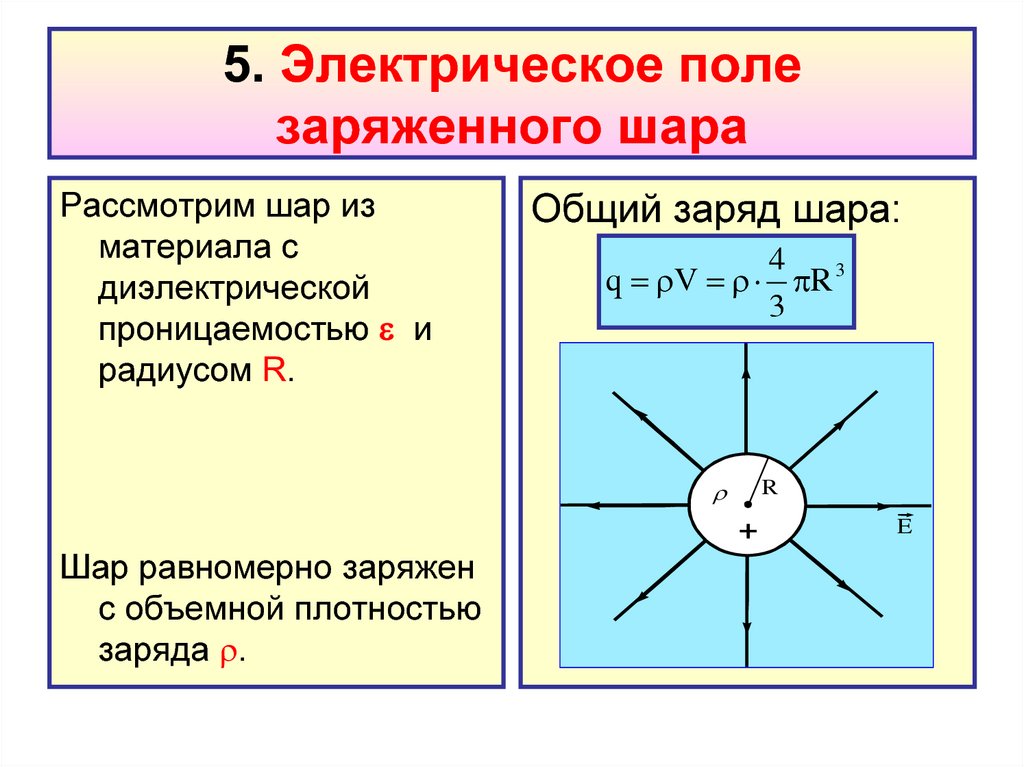
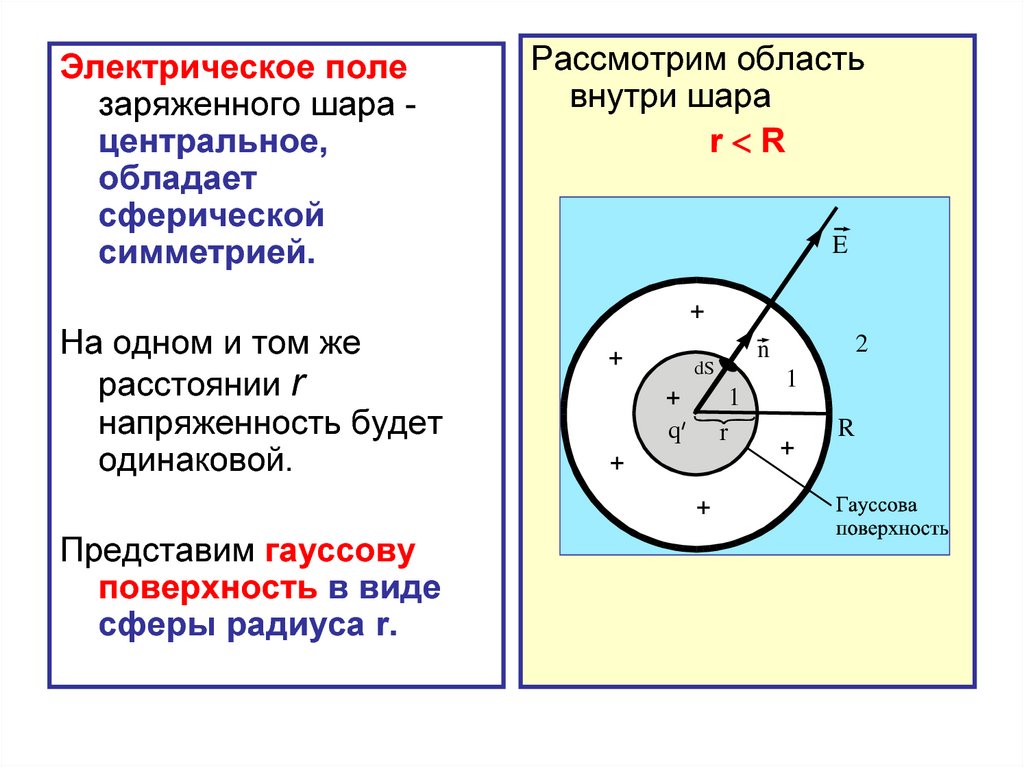
37. 5. Электрическое поле заряженного шара
Рассмотрим шар изматериала с
диэлектрической
проницаемостью и
радиусом R.
Общий заряд шара:
4 3
q V R
3
R
q+
Шар равномерно заряжен
с объемной плотностью
заряда .
E
38.
Электрическое полезаряженного шара центральное,
обладает
сферической
симметрией.
На одном и том же
расстоянии r
напряженность будет
одинаковой.
Рассмотрим область
внутри шара
r R
E
+
+
dS
1
+
q
r
+
+
Представим гауссову
поверхность в виде
сферы радиуса r.
2
n
1
+
R
39.
Линии напряженности пересекают гауссовуповерхность.
Вектор E и вектор нормали n к элементу
сферической поверхности совпадают по
направлению в любой точке гауссовой поверхности,
поэтому
O
E n E cos 0 E
Поток вектора через сферическую гауссову
поверхность равен
N
гаусс.
пов.
Е п dS Е dS Е 4 r
S
2
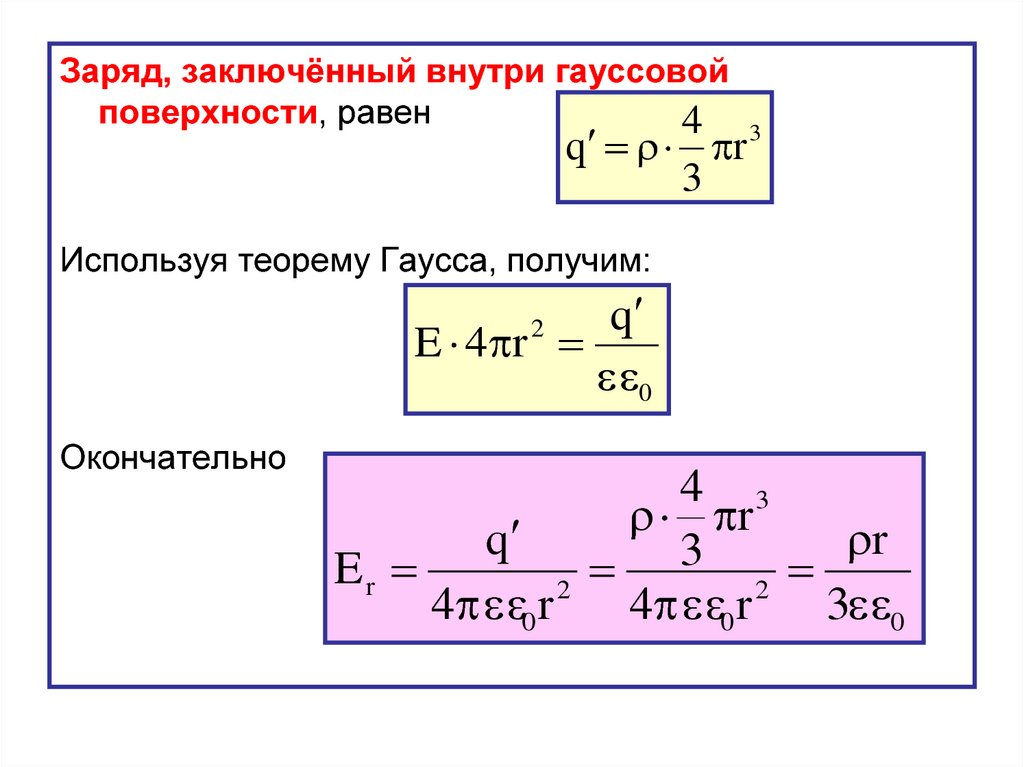
40.
Заряд, заключённый внутри гауссовойповерхности, равен
4
3
q r
3
Используя теорему Гаусса, получим:
q
E 4 r
0
2
Окончательно
4 3
r
q
r
3
Er
2
2
4 0 r
4 0 r
3 0
41.
В точках, лежащих на самой поверхности шара (r = R),напряженность равна
R
ER
3 0
Таким образом, для точек, лежащих внутри шара,
напряженность линейно возрастает с
увеличением расстояния от нулевого значения в
центре шара, до значения на его поверхности.
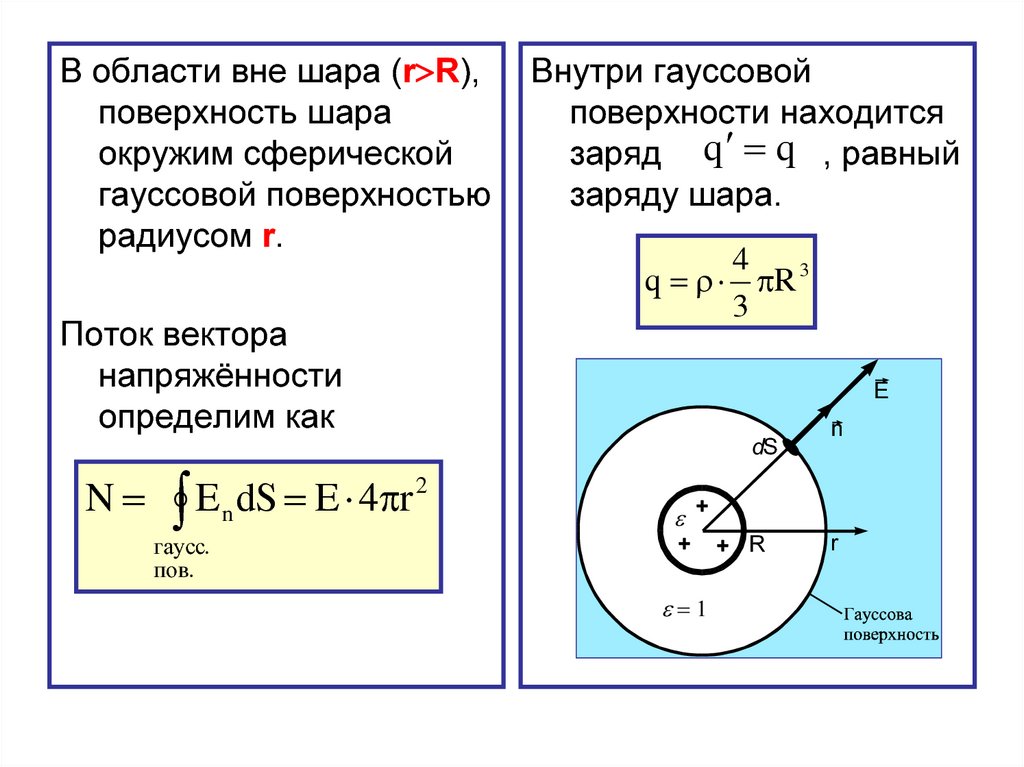
42.
В области вне шара (r R),поверхность шара
окружим сферической
гауссовой поверхностью
радиусом r.
Поток вектора
напряжённости
определим как
Внутри гауссовой
поверхности находится
заряд q q , равный
заряду шара.
4 3
q R
3
E
dS
N
2
E
dS
E
4
r
n
гаусс.
пов.
n
+
+
+ R
r
43.
Объединяя полученные формулы теоремой Гаусса,получим
4 3
R
E 4 r 2 3
0
В области вне шара точки пространства находятся в
воздухе, поэтому величина = 1.
R
E(r )
3 0 r 2
3
В точках, лежащих на самой поверхности шара (r = R),
напряжённость равна
R
E R
3 0
44.
Напряженность поля вне шара уменьшается сувеличением расстояния обратно
пропорционально квадрату расстояния (Е 1 / r 2 ).
Сравним формулы
R
ER
3 0
и
R
E R
3 0
Они дают значения напряженности на поверхности
шара: эти значения не равны между собой.
Это говорит о том, что напряженность в точках на
поверхности шара испытывает скачок.
.
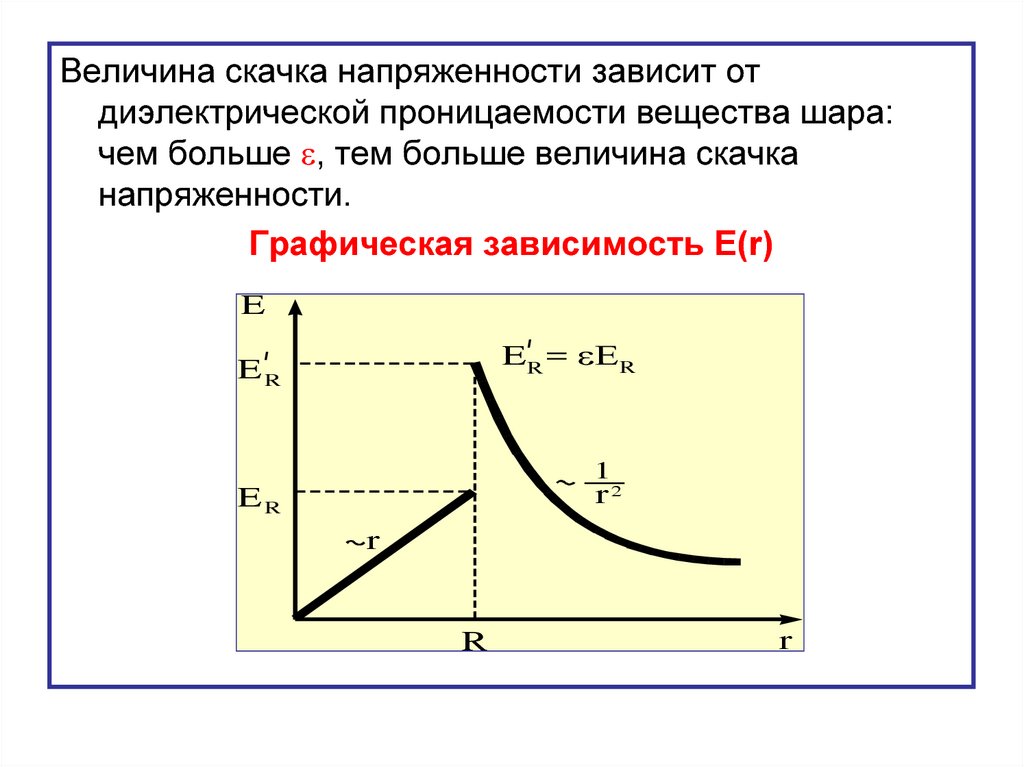
45.
Величина скачка напряженности зависит отдиэлектрической проницаемости вещества шара:
чем больше , тем больше величина скачка
напряженности.
Графическая зависимость Е(r)
E
ER = R
ER
1
r2
ER
r
R
r
46.
При расчете потенциала надо определить ту точку, вкоторой потенциал равен нулю.
Такая точка находится в бесконечности.
Тогда для области (r > R) на основе формулы связи
напряжённости с потенциалом имеем:
d Edr
r
r
0
d E(r)dr
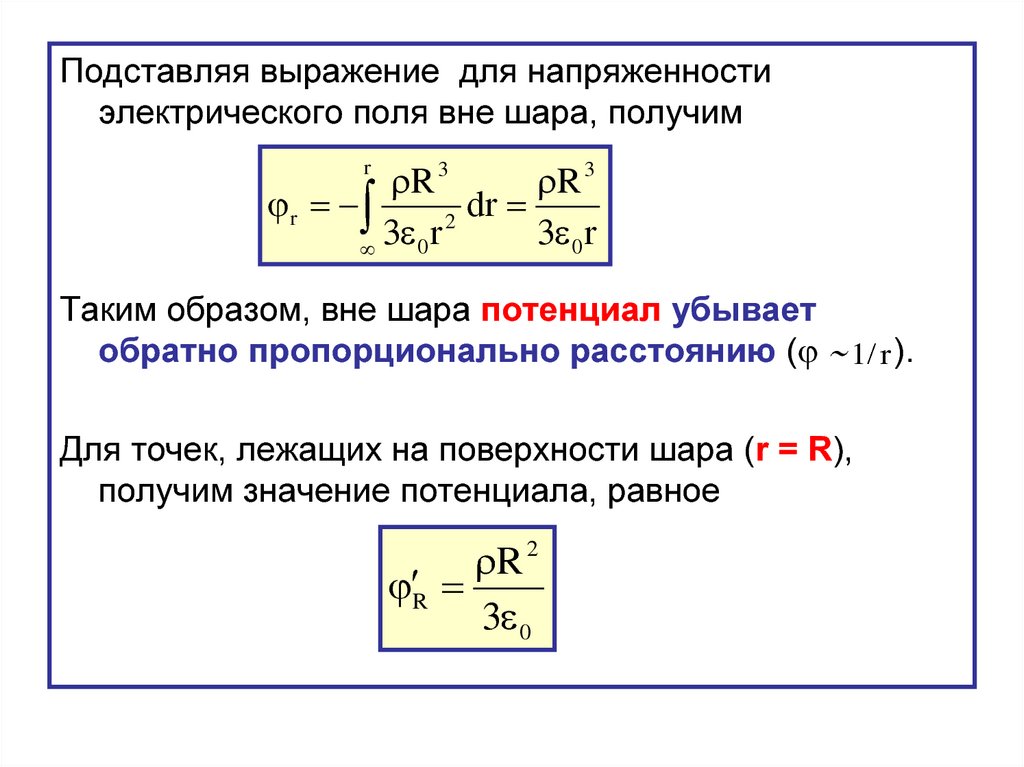
47.
Подставляя выражение для напряженностиэлектрического поля вне шара, получим
R 3
R 3
r
dr
2
3 0 r
3 0 r
r
Таким образом, вне шара потенциал убывает
обратно пропорционально расстоянию ( 1/ r ).
Для точек, лежащих на поверхности шара (r = R),
получим значение потенциала, равное
R 2
R
3 0
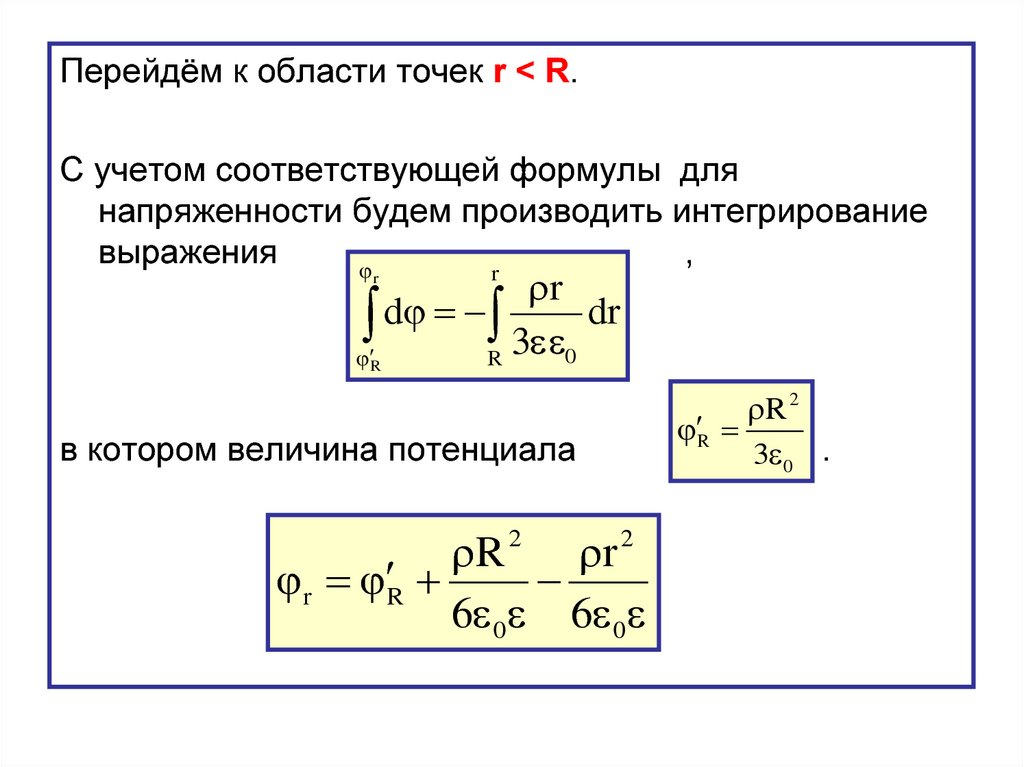
48.
Перейдём к области точек r < R.С учетом соответствующей формулы для
напряженности будем производить интегрирование
выражения
,
r
r
d R 3 0 dr
R
r
в котором величина потенциала
R 2 r 2
r R
6 0 6 0
R 2
R
3 0 .
49.
R 2 R 2 r 2 R 2 (1 2 ) r 2r
3 0 6 0 6 0
6 0
6 0
Зависимость (r) для точек внутри шара является
квадратичной.
R 2 (1 2 )
При r = 0 потенциал имеет значение: 0
6 0
Потенциал – функция непрерывная и не должна
испытывать скачков.
50.
Графическая зависимость (r)0
R
R
r
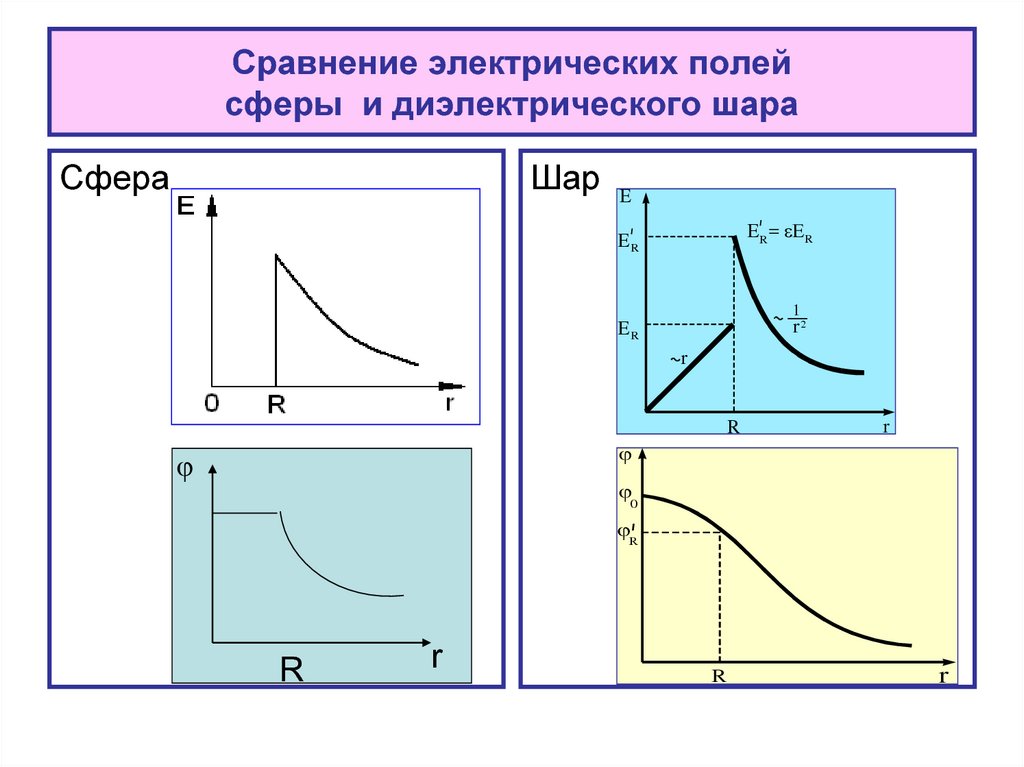
51. Сравнение электрических полей сферы и диэлектрического шара
СфераШар
E
ER = R
ER
1
r2
ER
r
R
r
0
R
R
r
R
r




























 Физика
Физика








