Векторная алгебра (1 часть). Векторы на плоскости и в пространстве

1. Векторная алгебра. (1 часть)

2. 1. Векторы на плоскости и в пространстве

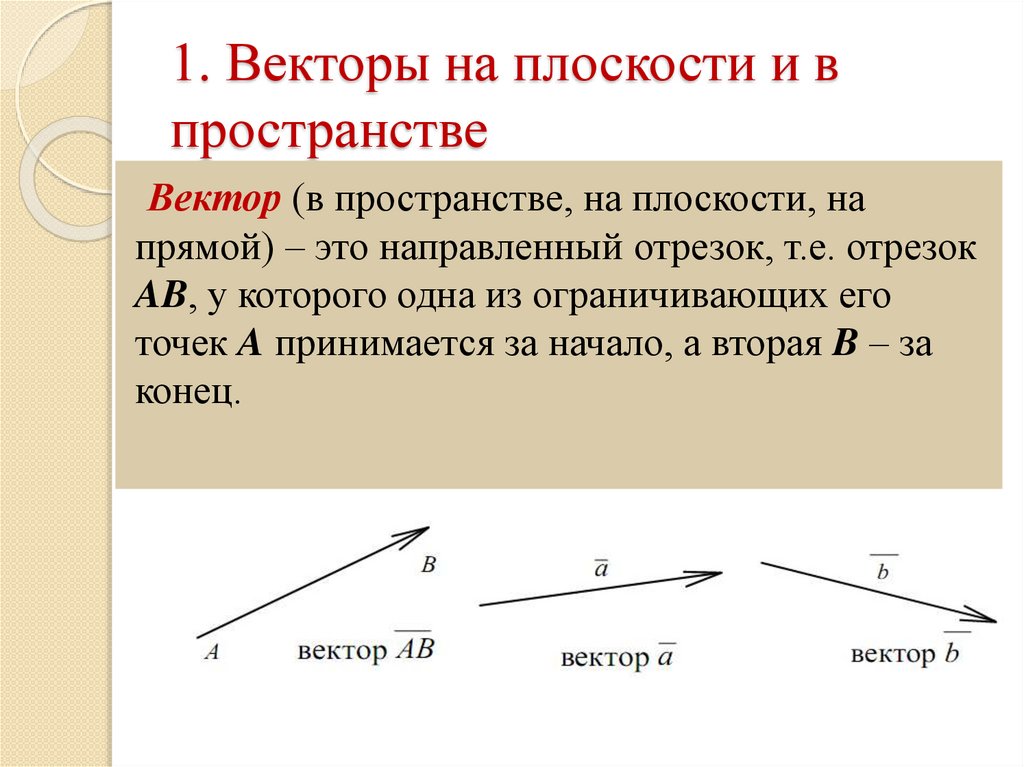
Вектор (в пространстве, на плоскости, на
прямой) – это направленный отрезок, т.е. отрезок
AB, у которого одна из ограничивающих его
точек A принимается за начало, а вторая B – за
конец.

3. Модулем вектора (длиной вектора) называется длина отрезка :

a AB
Нулевым вектором называется вектор, у которого
начало и конец совпадают.
0 0
! Направление нулевого вектора не
определено.

4.

Ненулевые векторы AB и CD называются
равными: AB CD , если:
1) они лежат на одной прямой или на
параллельных прямых;
2) имеют одинаковые длины ( AB CD ) и
одинаково направлены.
! Все нулевые векторы считаются равными
B
D
друг другу.
A
C

5.

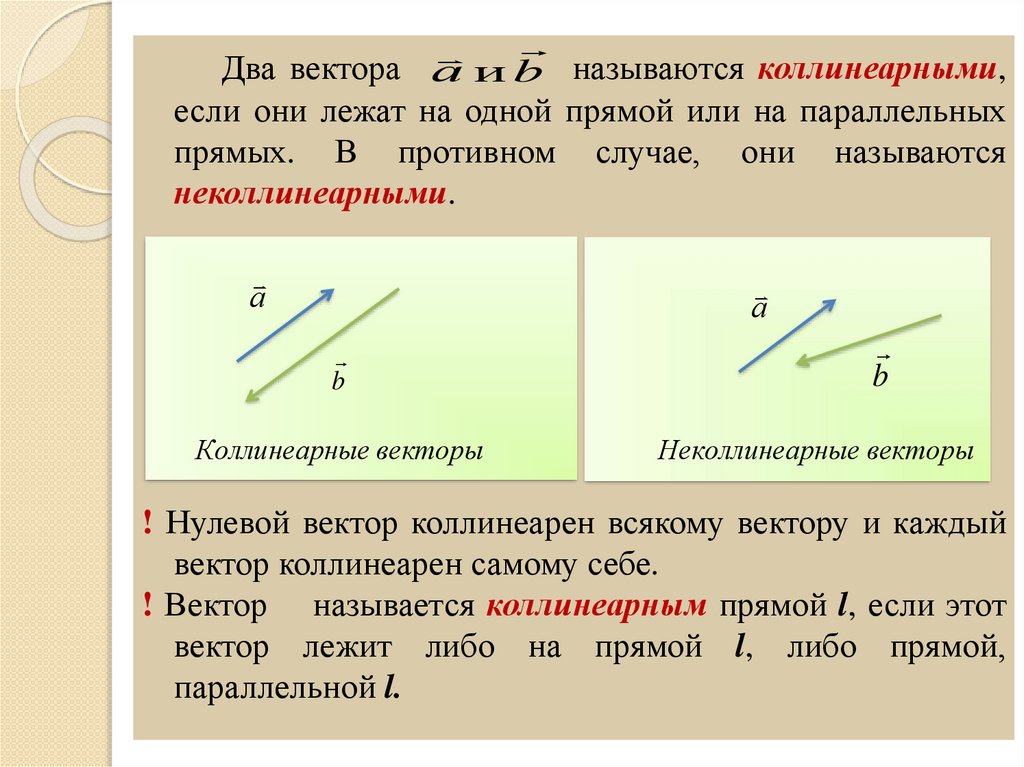
Два вектора а и b называются коллинеарными,
если они лежат на одной прямой или на параллельных
прямых. В противном случае, они называются
неколлинеарными.
а
а
b
Коллинеарные векторы
b
Неколлинеарные векторы
! Нулевой вектор коллинеарен всякому вектору и каждый
вектор коллинеарен самому себе.
! Вектор называется коллинеарным прямой l, если этот
вектор лежит либо на прямой l, либо прямой,
параллельной l.

6.

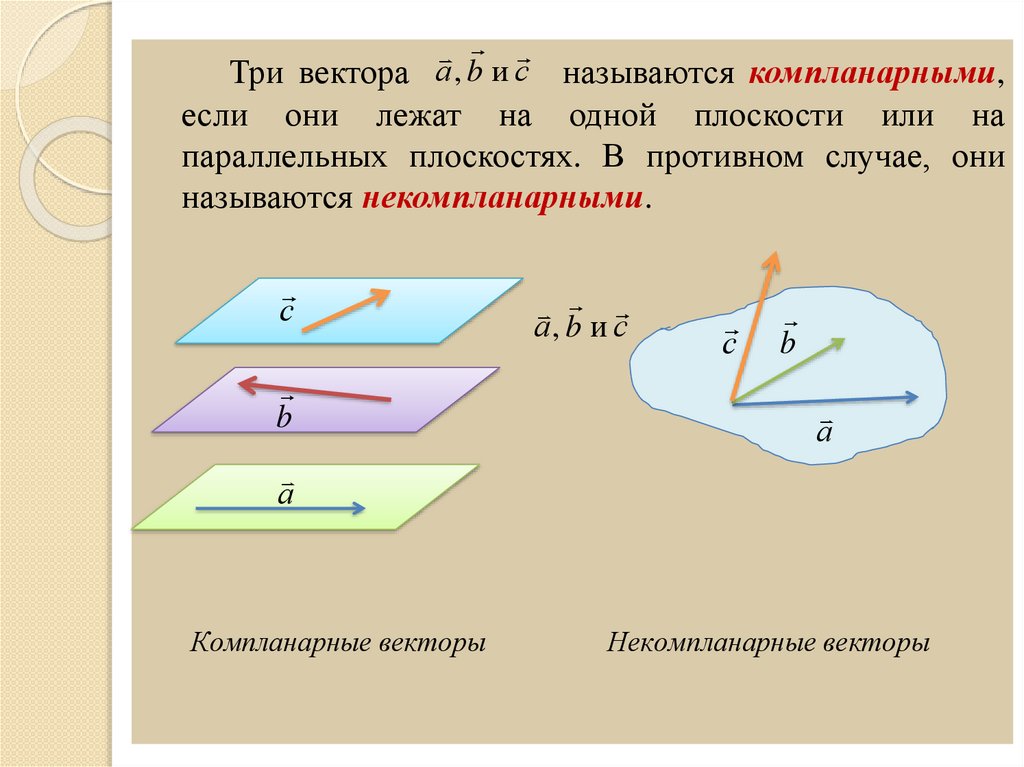
Три вектора а , b и с называются компланарными,
если они лежат на одной плоскости или на
параллельных плоскостях. В противном случае, они
называются некомпланарными.
с
b
а, b и с
с
b
а
а
Компланарные векторы
Некомпланарные векторы

7.

а, b и с
! Если хоть один из векторов
вектор, то эти векторы компланарны.
нулевой
! Множество всех свободных векторов на
1
прямой будем обозначать R , на плоскости R 2, в пространстве - R3 .
! Вектор равный исходному по длине и
имеющий противоположное направление
называется противоположным вектором.
a

8. 2. Линейные операции над векторами

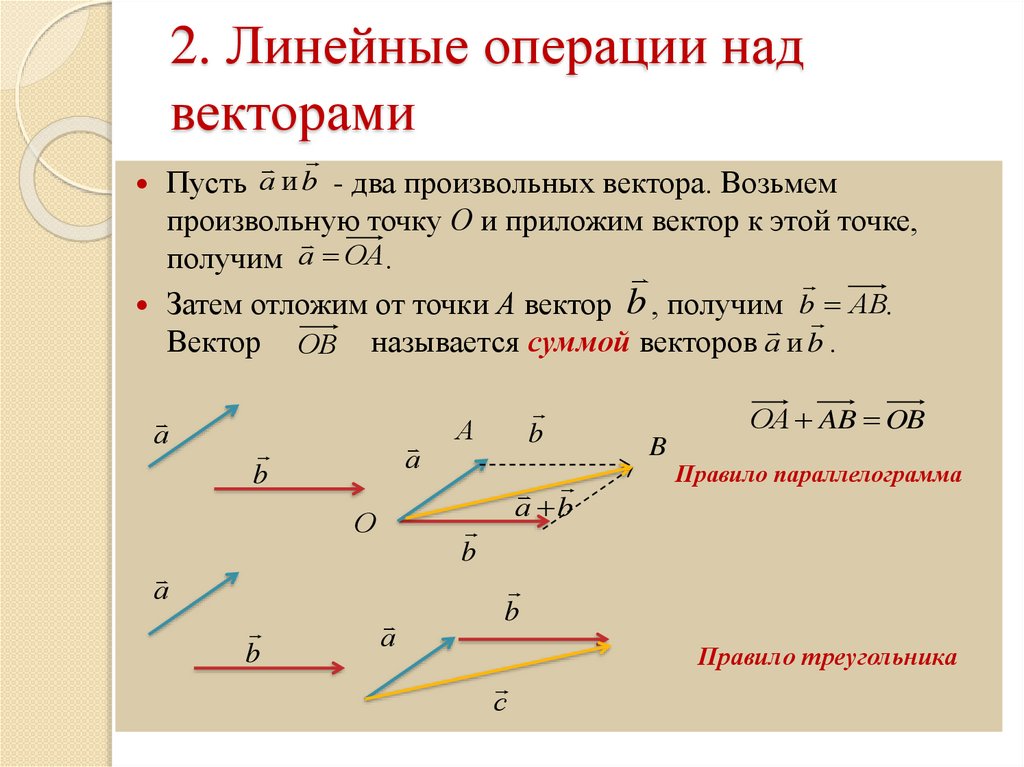
Пусть а и b - два произвольных вектора. Возьмем
произвольную точку О и приложим вектор к этой точке,
а
получим ОA.
Затем отложим от точки А вектор b , получим b АB.
Вектор ОB называется суммой векторов а и b .
а
а
b
О
А
а b
b
а
b
b
а
ОА AB OB
B
Правило параллелограмма
b
с
Правило треугольника

9.

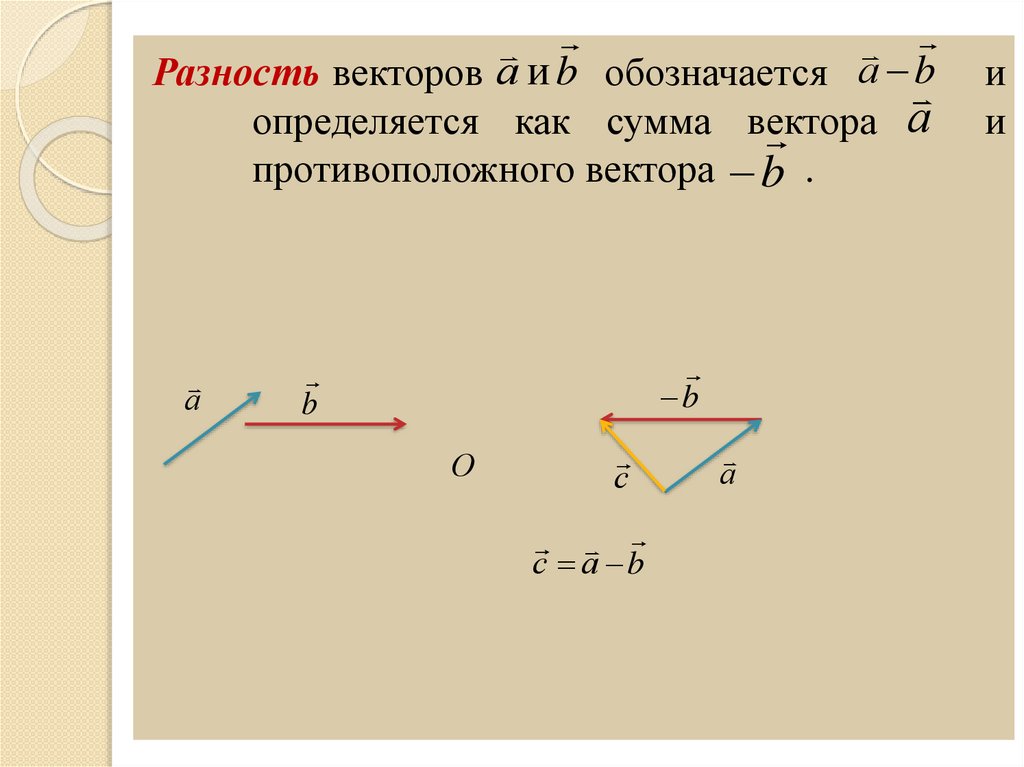
Разность векторов а и b обозначается а b
а
определяется как сумма вектора
противоположного вектора b .
а
b
b
О
с
с а b
а
и
и

10.

Произведение вектора а на число называется вектор,
а
длина которого равна числу
и который
имеет направление вектора а , если >0, и
противоположное направление ( а ), если 0.
Обозначается: а .
Если 0 или а 0 , то а 0 .
а
3а
2а

11. 3. Свойства линейных операций над векторами

1. a b b a
2. (a b) c a (b c)
3. a ( a) 0
4. (a b) a b
5. ( 1 2 )a 1 a 2 a
6. ( 1 2 )a 1 ( 2 a)
7. a 0 a 0 a
8. a b a b
9. a b a b

12. 4. Разложение векторов на плоскости

Теорема: Пусть векторы a и b −
неколлинеарные, векторы
a, b, c - компланарные.
Тогда найдутся такие постоянные
и
,что
c a b
Такое разложение единственное.
Доказательство:
p
q
c p q
a
p a
c
b
q b
c a b

13.

Докажем единственность.
Предположим, что разложение не единственно,
тогда:
c a b
c 1 a 1 b
1
(хотя бы одно из неравенств
1 и 1 выполнено)
0 ( 1 )a ( 1 )b
( 1 )
b
a
( 1 )
b a
(противоречие)

14. 5. Разложение векторов в пространстве

Теорема: Пусть векторы a , b, c
некомпланарные.
−
Тогда найдутся такие постоянные , , ,
что любой вектор d
можно записать в виде
d a b c
(разложить по векторам a , b, c ).
Такое разложение единственное.

15. 6. Базис и линейная комбинация векторов

Базисом в пространстве называются любые 3
некомпланарных
вектора,
взятые
в
определенном порядке.
Базисом на плоскости называются любые 2
неколлинеарных
вектора,
взятые
в
определенном порядке.
Базисом на прямой называется любой ненулевой
вектор.

16. Если - базис в пространстве и , то числа ,  и  - называются компонентами или координатами вектора в этом базисе.

Если e1 , e2 , e3 - базис в пространстве и a e1 e2 e3 ,
то числа , и - называются компонентами или
координатами вектора в этом базисе.
Свойства:
1. Равные векторы имеют одинаковые координаты.
2. При умножении вектора на число его компоненты
тоже умножаются на это число:
a ( e1 e2 e3 ) ( )e1 ( ) e2 ( ) e3
3. При сложении векторов складываются их
соответствующие компоненты:
a 1 e1 2 e2 3 e3
b 1 e1 2 e2 3 e3
( 1 1 )e1 ( 2 2 )e2 ( 3 3 )e3

17.

Если a1 , a2 ,..., an- некоторая система векторов
3
1 2
пространства R ( R , R или R ), тогда любой
вектор вида 1a1 2 a2 ... n an называется
линейной комбинацией векторов
a1 , a2 ,..., an , где 1 , 2 ,..., п
некоторые действительные числа, называемые
коэффициентами линейной комбинации.
! Если какой-либо вектор представляется в
виде линейной комбинации некоторых
векторов, то говорят, что он разложен по этим
векторам.

18.

Векторы a1 ,..., a n называются
линейно
зависимыми, если существует такая линейная
комбинация 1 a1 2 a2 ... n an 0 , при не равных
нулю одновременно i , т.е. 12 22 ... n2 0 .
Если же только при i = 0 выполняется
равенство 1 a1 2 a2 ... n an 0 , то векторы
называются линейно независимыми.

19.

Свойства:
1. Если среди векторов есть нулевой вектор, то эти
векторы линейно зависимы.
2. Если к системе линейно зависимых векторов добавить
один или несколько векторов, то полученная система
тоже будет линейно зависима.
3. Система векторов линейно зависима тогда и только
тогда, когда один из векторов раскладывается в линейную
комбинацию остальных векторов.
4. Любые 2 коллинеарных вектора линейно зависимы и,
наоборот, любые 2 линейно зависимые векторы
коллинеарны.
5. Любые 3 компланарных вектора линейно зависимы и,
наоборот, любые 3 линейно зависимые векторы
компланарны.
6. Любые 4 вектора линейно зависимы.