Система координат. Географические координаты

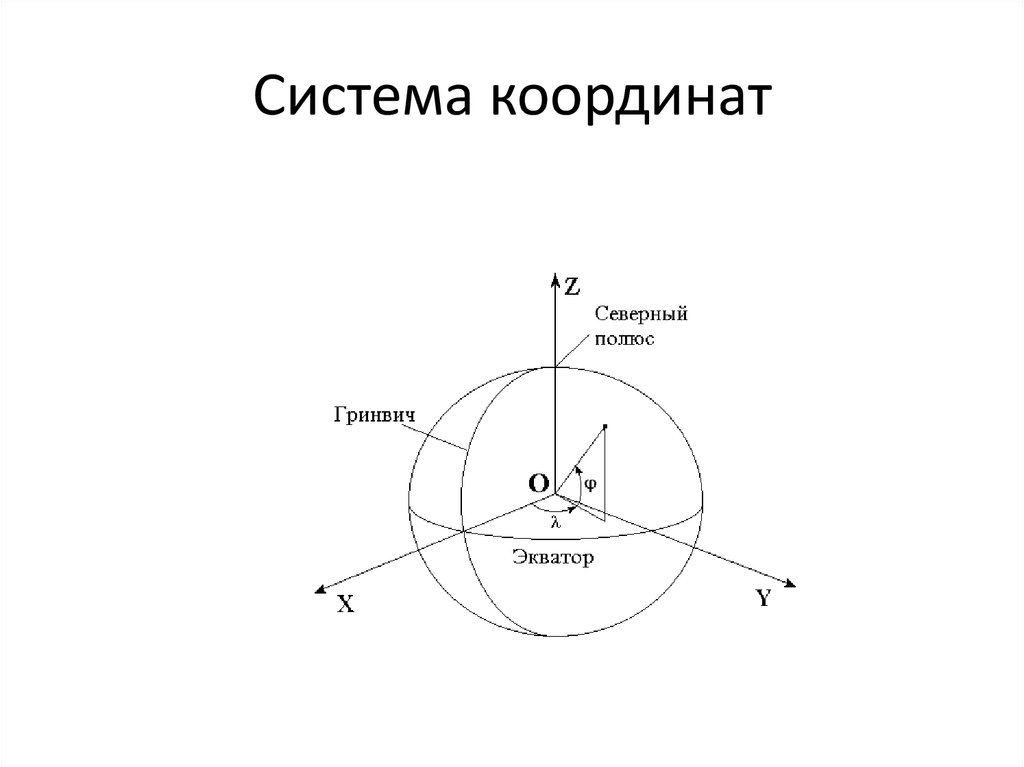
1. Система координат

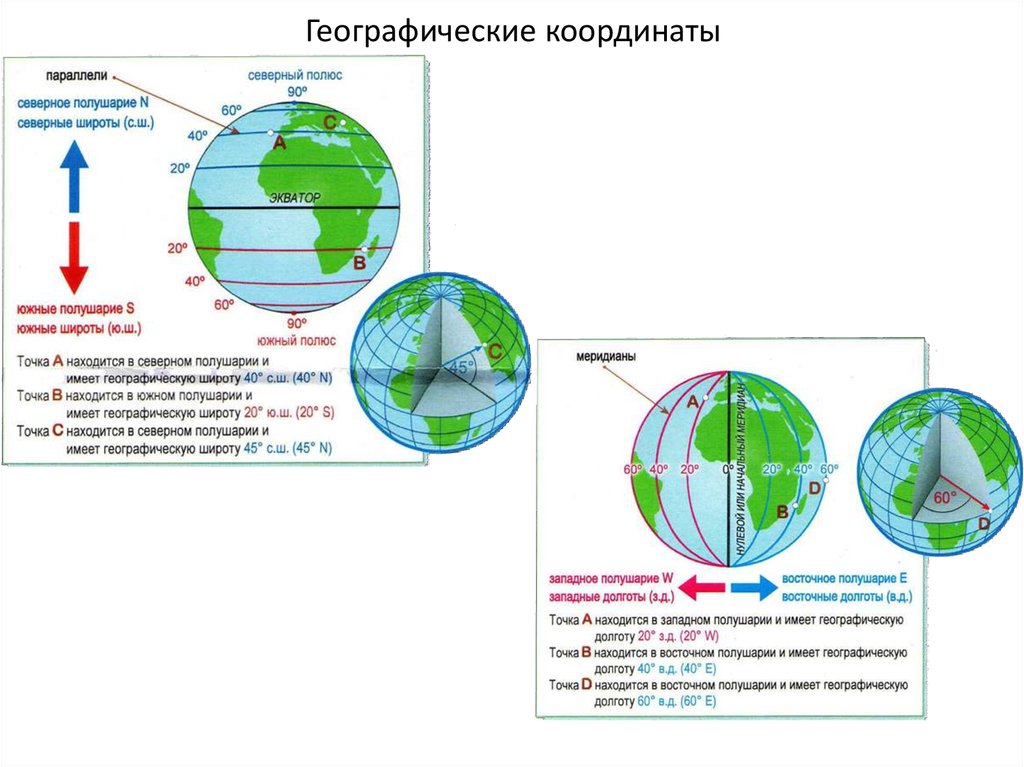
2. Географические координаты

3. Параметры эллипсоида Земли

Малая полуось (полярный радиус), b
6356863,019 м
Большая полуось (экваториальный радиус), a
6378245,000 м
Средний радиус Земли, принимаемой за шар, Rз
6371100 м
Полярное сжатие (отношение разницы полуосей к большой полуоси), a 1/298,3
Площадь поверхности Земли
510 083 058 км²
Длина меридиана
40 008 550 м
Длина экватора
40 075 696 м
Длина дуги 1° по меридиану на широте 0°
110,6 км
Длина дуги 1° по меридиану на широте 45°
111,1 км
Длина дуги 1° по меридиану на широте 90°
111,7 км

4. Преобразования географических координат в геоцентрические (h=0)

X = R çcos cos ,
Y = R çcos sin ,
Z = R çsin ,
где Rз – радиус Земли,
– широта, – долгота
.

5. Преобразование в геоцентрические координаты ( )

Преобразование в геоцентрические координаты ( H 0 )
x ( N H) cos(B) cos(L)
y ( N H) cos(B) sin( L)
z (1 e 2 ) N H sin( B)
N
a
1 e 2 sin 2 ( B)
e 1 b2 a2
Преобразование в географические координаты
переход от пространственных координат X, Y, Z к географическим
B, L, H требует выполнения итераций
при вычислении широты B и высоты H. Для этого используют
следующий алгоритм:
вычисляют вспомогательную величину D
D x 2 y2

6.

•анализируют значение D.
•Если D=0, то
B
z
, L 0, H z sin( B) a 1 e 2 sin 2 (B) .
2z
если y 0, x 0, то L 2 L a ,
если y 0, x 0, то L L a ,
если y 0, x 0, то L L a ,
если y 0, x 0, то L L a ,
y
L a arcsin
D
Если D>0, то
анализируют значение z.
Если z=0, то
B 0, H D a
Во всех других случаях используют следующий алгоритм вычислений:
находят вспомогательные величины r, c, p по формулам:
e 2a
z
r x y z , c arcsin , p
2r
r
реализуют итеративный процесс:
2
2
2
s1 0,
если модуль разности
s 2 s1
b c s1 ,
p sin( 2b)
s2 arcsin
2
2
1 e sin (b)
меньше заданной погрешности вычисления ε
B b,
H D cos(B) z sin( B) a 1 e 2 sin 2 B .

7.

Во всех других случаях используют следующий алгоритм вычислений:
находят вспомогательные величины r, c, p по формулам:
e 2a
z
r x y z , c arcsin , p
2r
r
2
2
2
реализуют итеративный процесс:
s1 0,
b c s1 ,
p sin( 2b)
s 2 arcsin
1 e 2 sin 2 (b)
если модуль разности
s 2 s1
меньше заданной погрешности вычисления ε