Похожие презентации:
Пересечение прямых и плоскостей
1. Пересечение прямых и плоскостей
Пересечение прямой спроецирующей плоскостью
2.
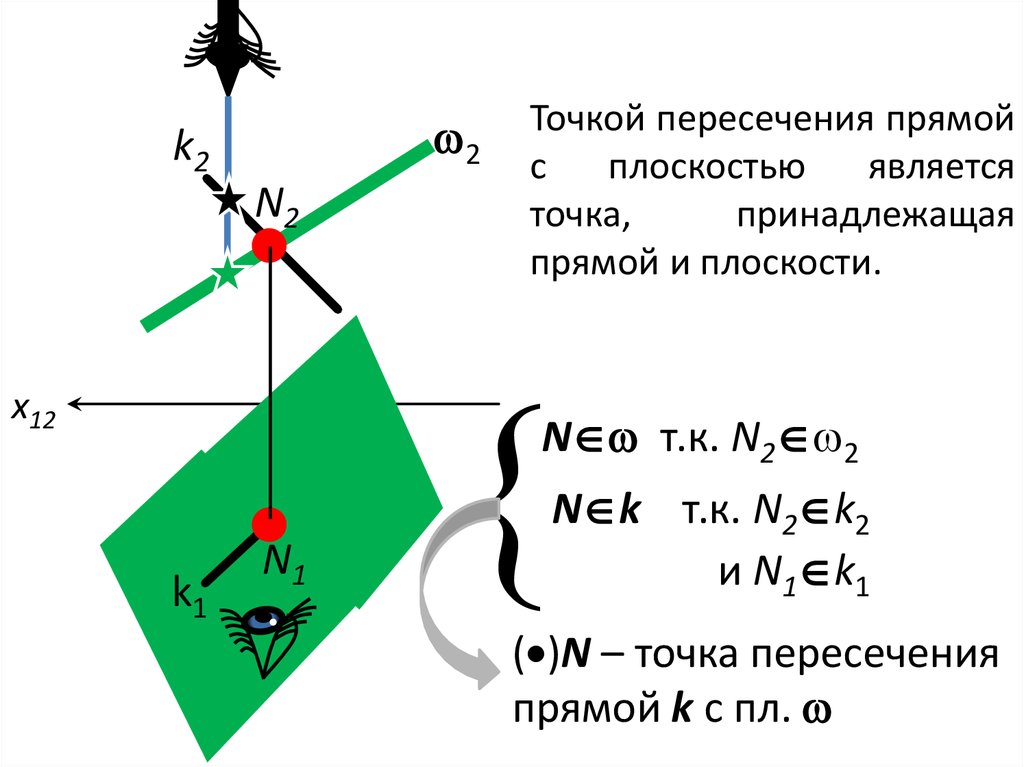
2k2
N2
x12
Точкой пересечения прямой
с
плоскостью
является
точка,
принадлежащая
прямой и плоскости.
N т.к. N2 2
k1
N1
N k т.к. N2 k2
и N1 k1
( )N – точка пересечения
прямой k c пл.
3.
Пересечение плоскости общегоположения с проецирующей
плоскостью
4.
1222
1
2
5.
1222
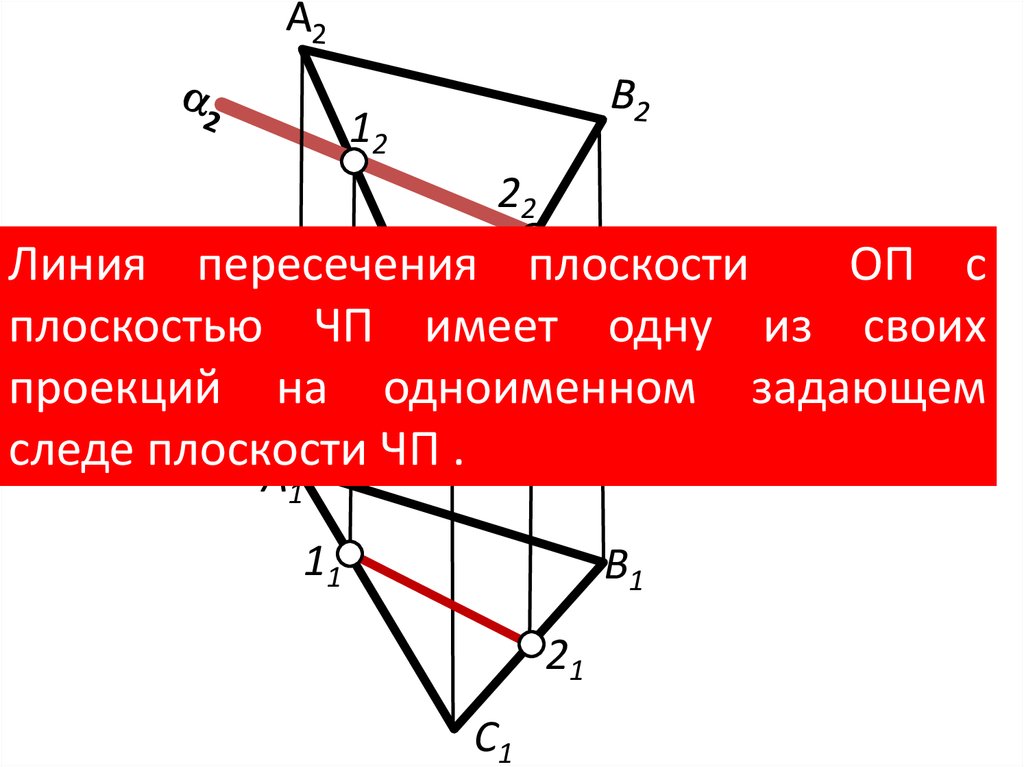
Линия пересечения плоскости
ОП с
плоскостью ЧП имеет одну из своих
проекций на одноименном задающем
x12 плоскости ЧП .
следе
A1
11
B1
21
C1
6.
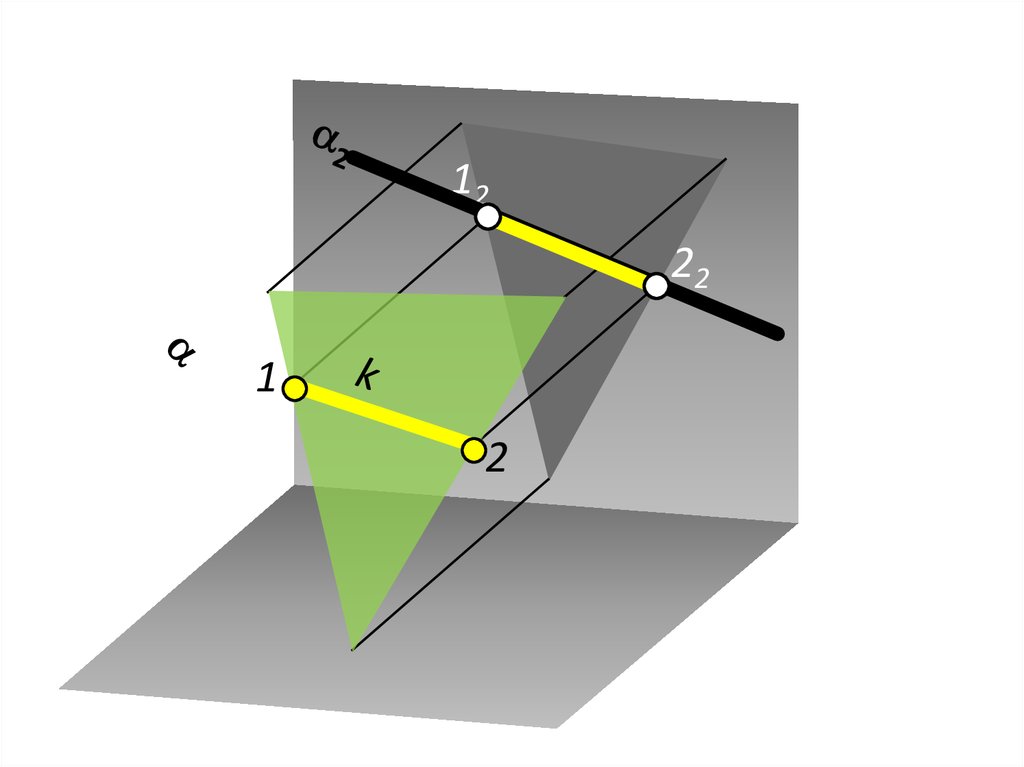
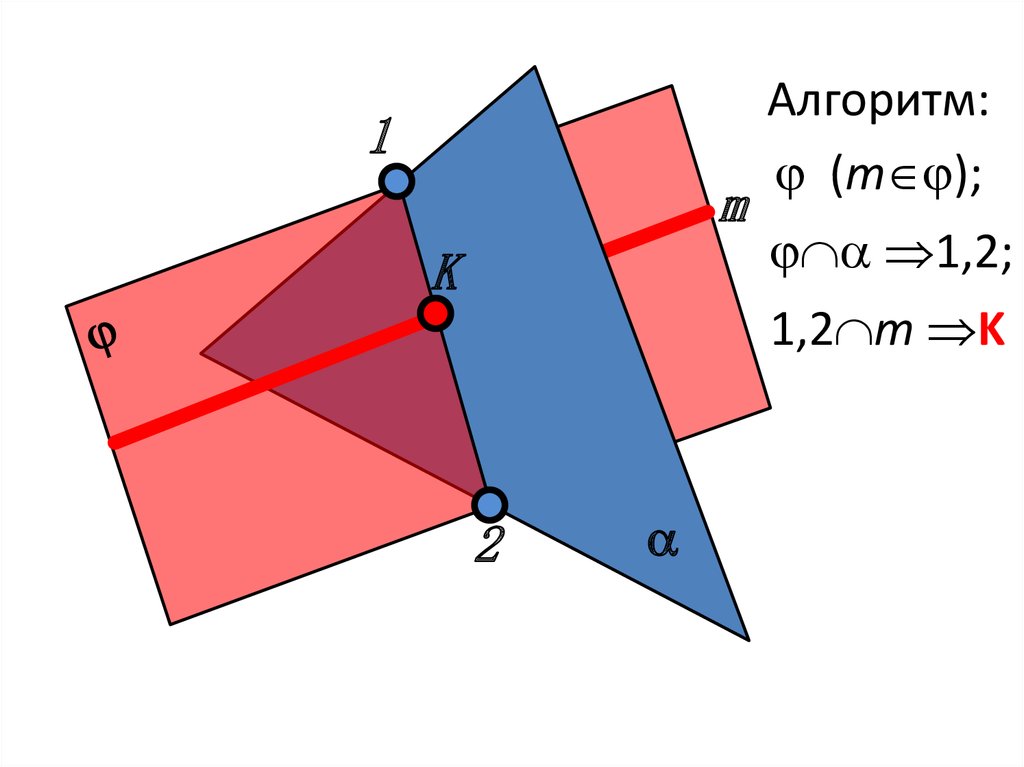
Пересечение прямой с плоскостьюобщего положения
7.
1m
K
Алгоритм:
(m );
1,2;
1,2 m K
2
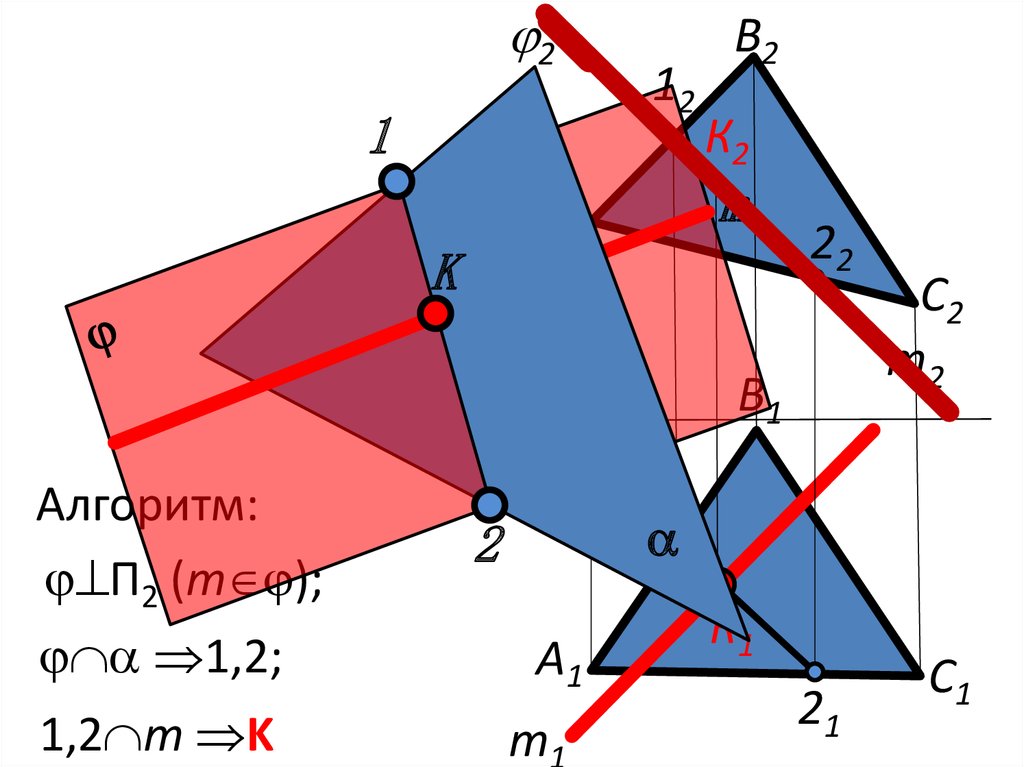
8.
21
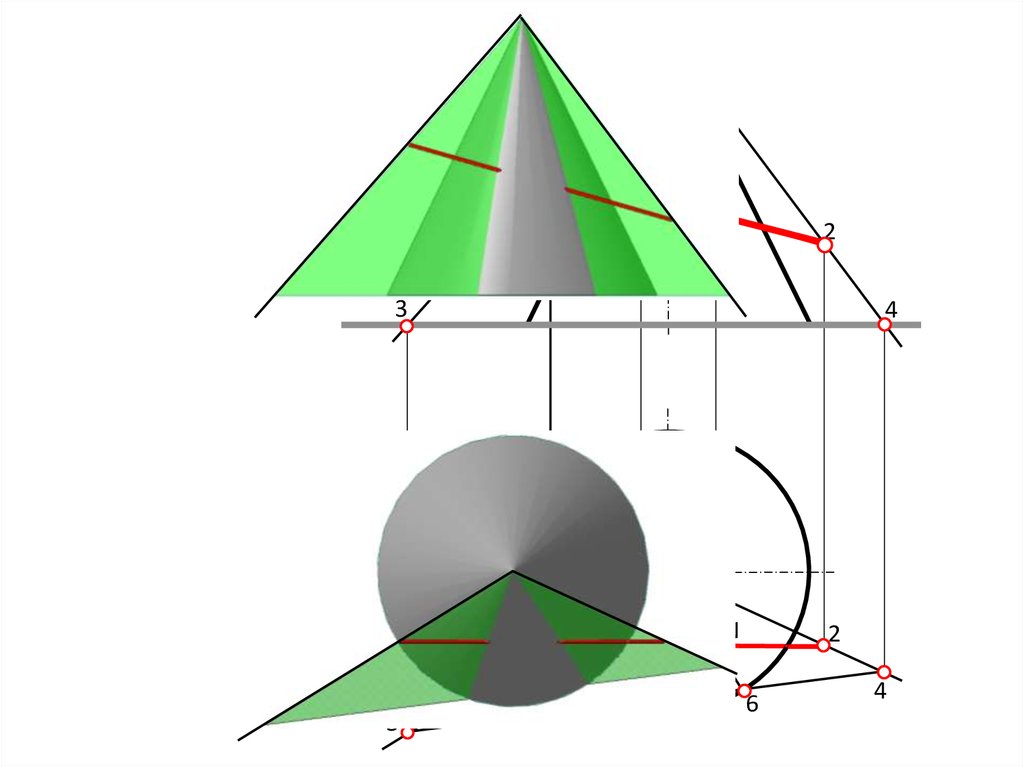
12
1,2;
1,2 m K
22
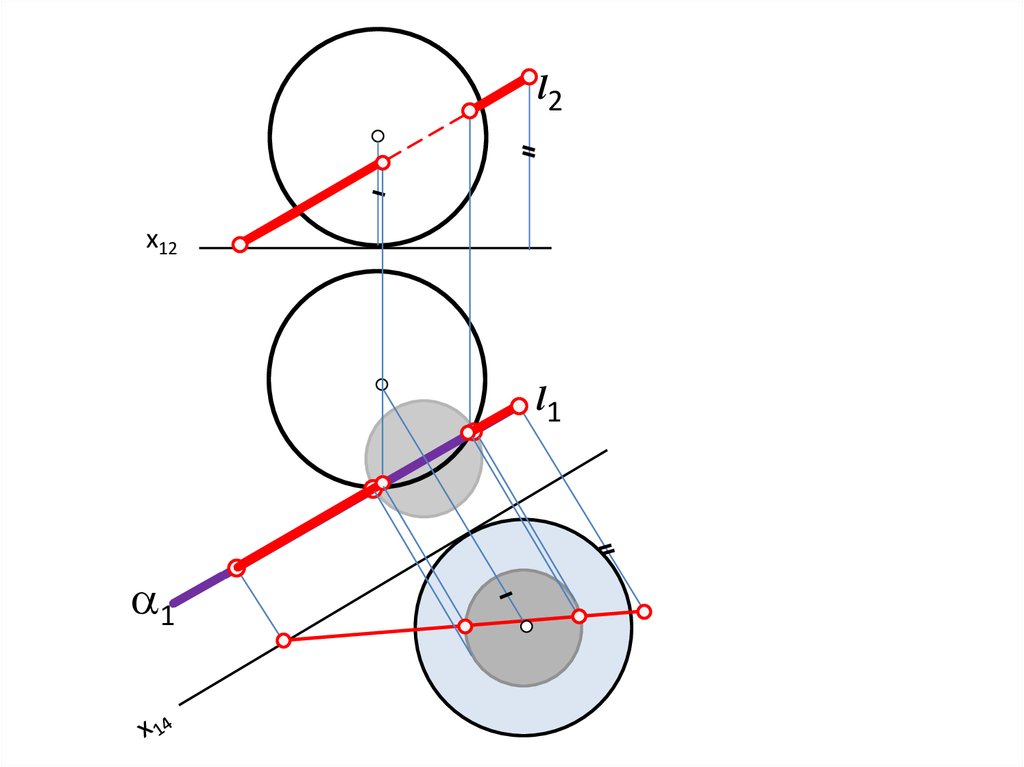
В1
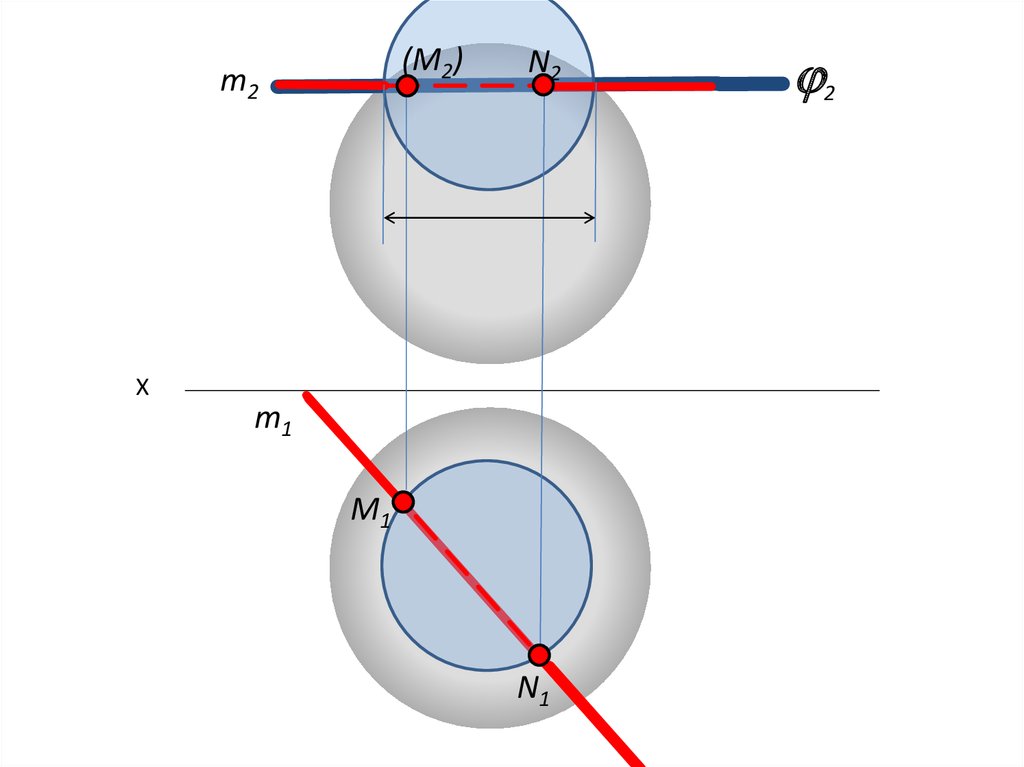
x12
Алгоритм:
П2 (m );
К2
m
А
K
В2
С2
m2
1
1
2
А1
m1
К1
21
С1
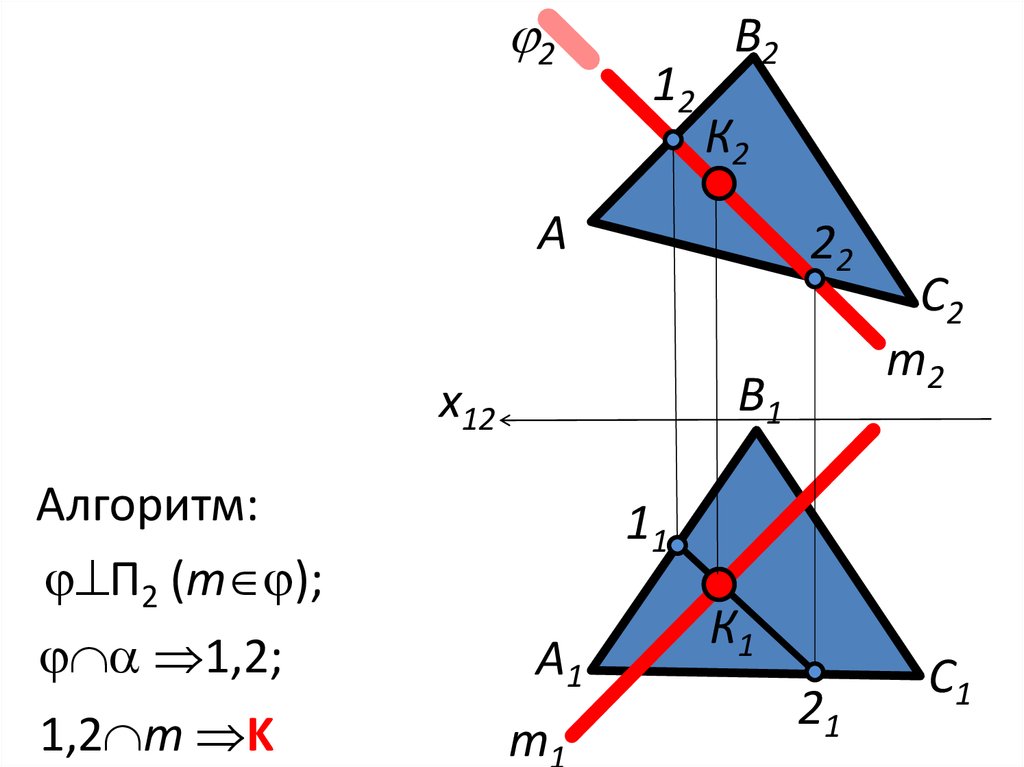
9.
212
В2
К2
А
22
В1
x12
Алгоритм:
П2 (m );
1,2;
1,2 m K
С2
m2
11
А1
m1
К1
21
С1
10. Пересечение проецирующих плоскостей
11.
k212.
k2k1
x12
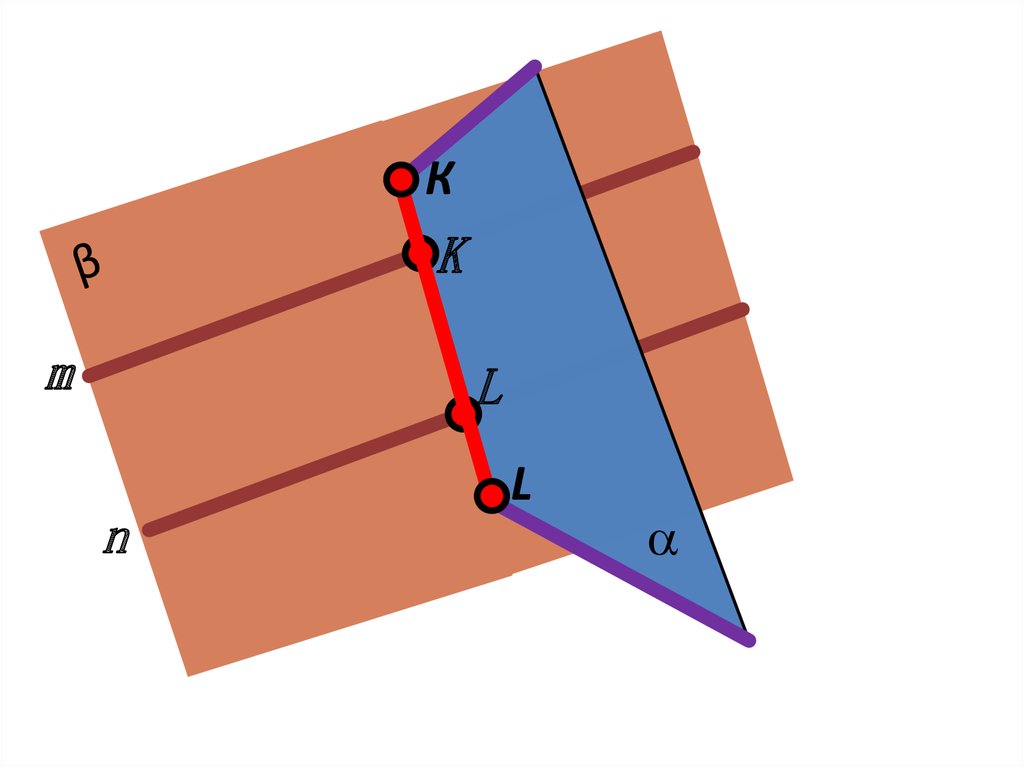
13. Построение линии пересечения двух плоскостей общего положения
14.
Km
L
n
15.
КK
m
L
n
L
16.
KПостроение линии пересечения двух
плоскостей
общего положения заключается в
m
определении точек пересечения
двух
L
прямых одной плоскости
с другой
n
плоскостью
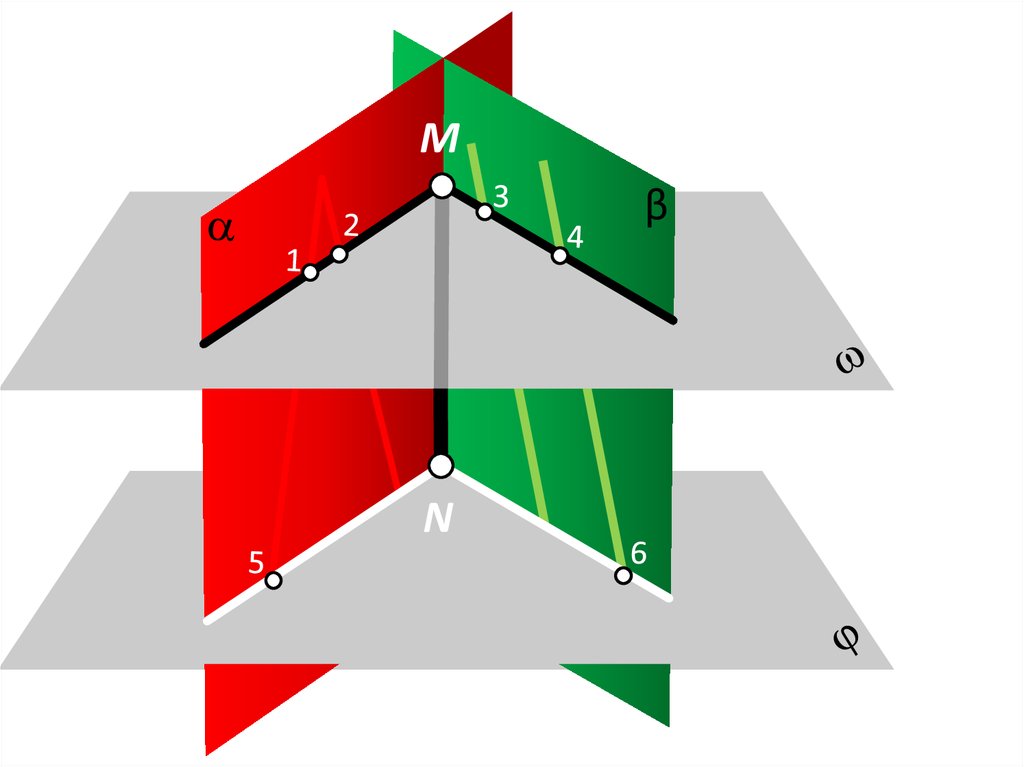
17.
Mβ
N
18.
f2e2
2
12
2
(a b)
β(eff)
ПП22
12
5…
34
β 6…
12 34 M
5… 6… N
M2
M
22
β
a2 52
a1
51
b2
11
b1
N
32
42
N2
62
61
41
21
N1
M1
31
e1
f1
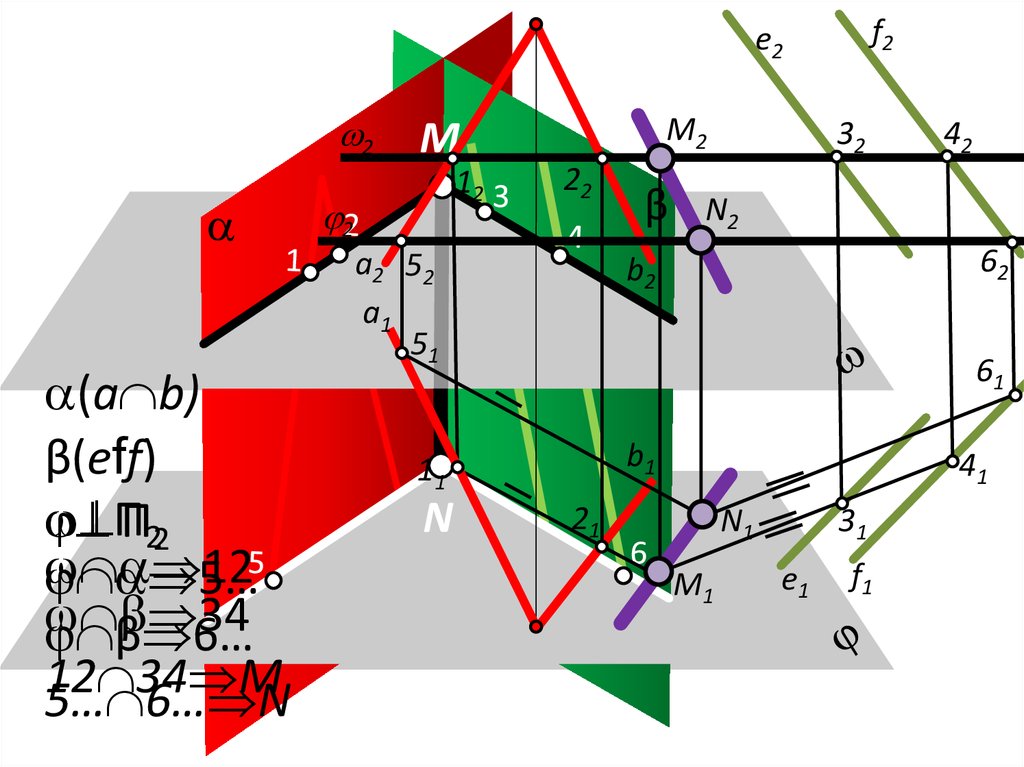
19.
Алгоритм построения линии пересечениядвух плоскостей общего положения
(a b) и β(eff)
П2
12 12 34 M
34
MN – линия
П2
пересечения
5…
5… 6… N
β 6…
плоскостей
и
20.
Пересечение плоскости спроецирующей плоскостью
21.
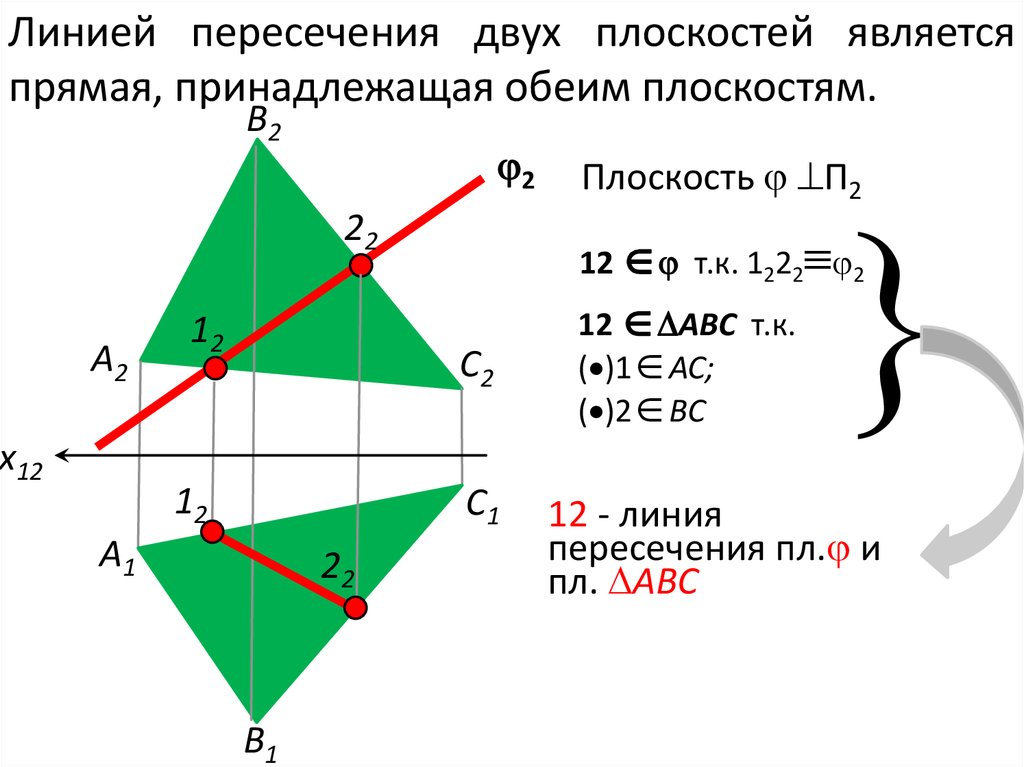
Линией пересечения двух плоскостей являетсяпрямая, принадлежащая обеим плоскостям.
В2
2
22
x12
12 т.к. 1222 2
С2
12
С1
А1
22
В1
12 АВС т.к.
( )1 АС;
( )2 ВС
А2
12
Плоскость П2
12 - линия
пересечения пл. и
пл. АВС
22. Определение видимости плоскостей
23.
В22
22
12
А2
x12
С2
12
С1
А1
22
В1
24. Пересечение поверхности плоскостью и прямой
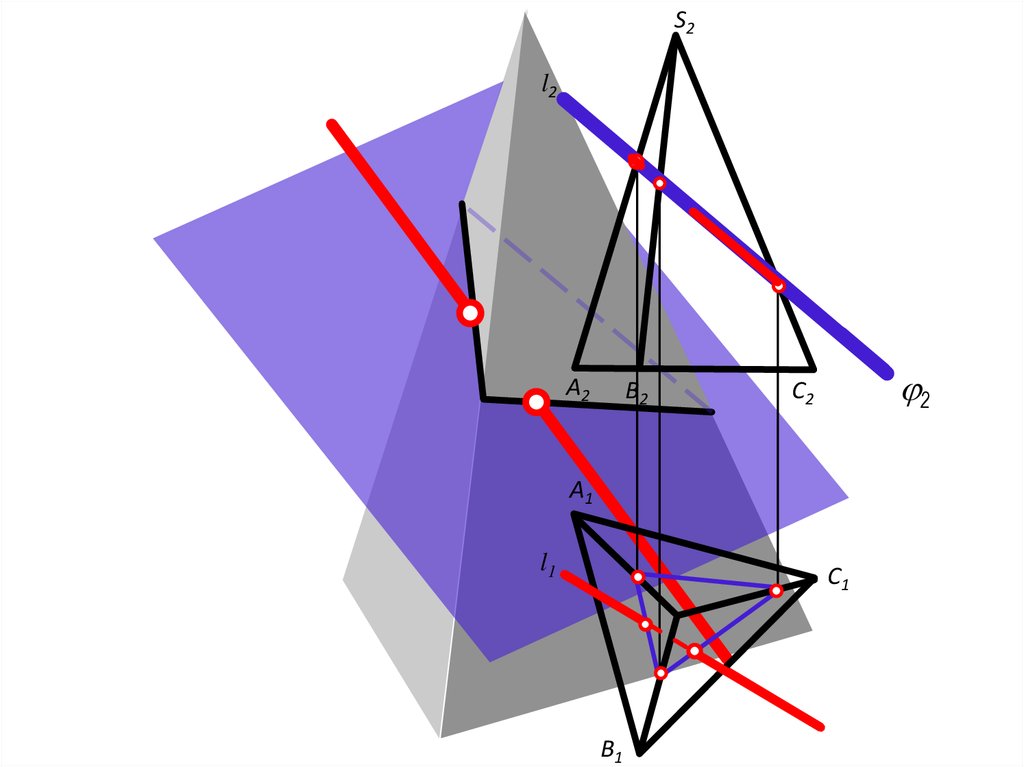
25. Пересечение проецирующей плоскости с поверхностью многогранника
26.
27.
S212
22
32
А2
В2
2
С2
A1
11
31
21
B1
C1
28.
Пересечение с линейчатойповерхностью
29.
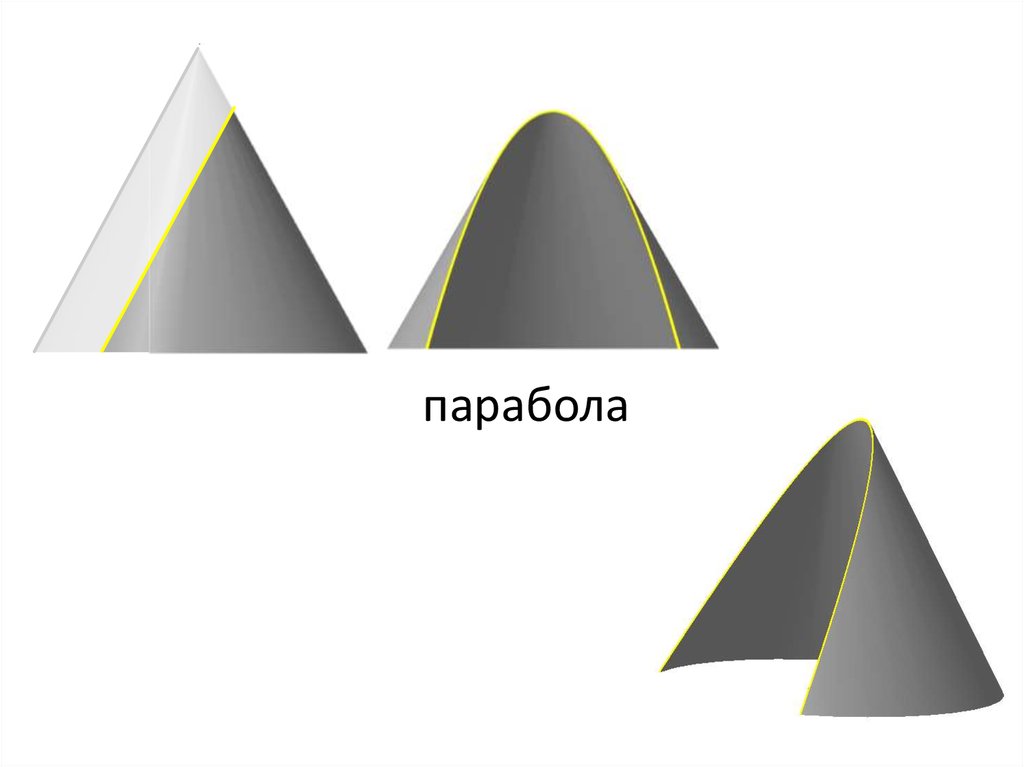
парабола30.
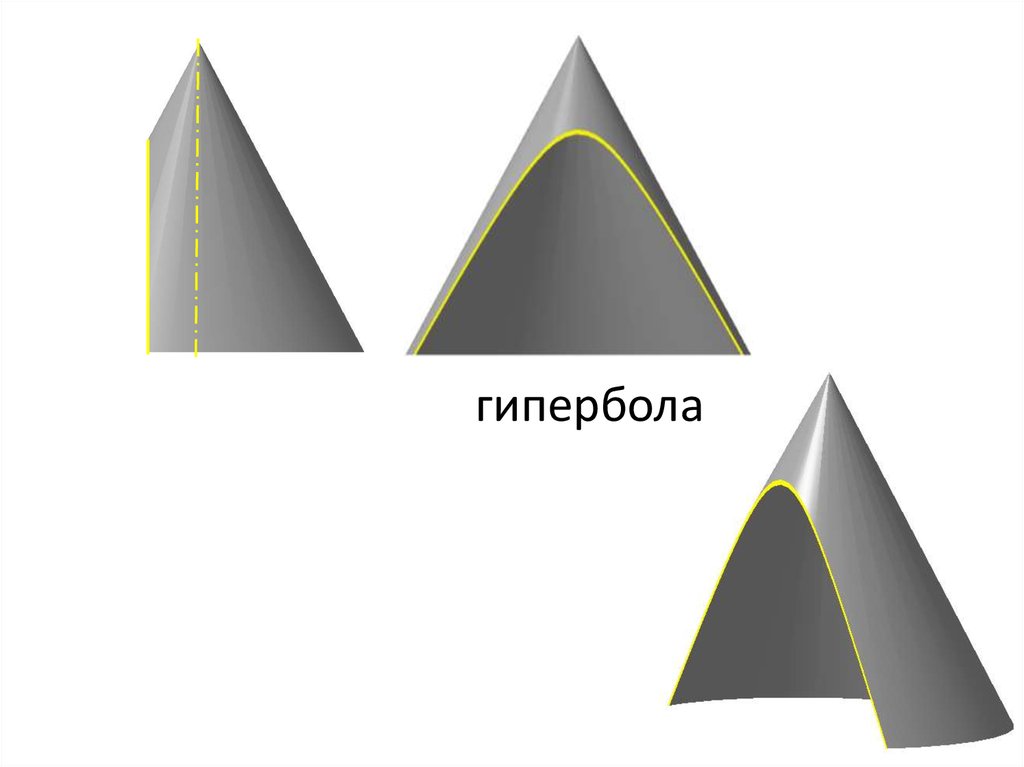
гипербола31.
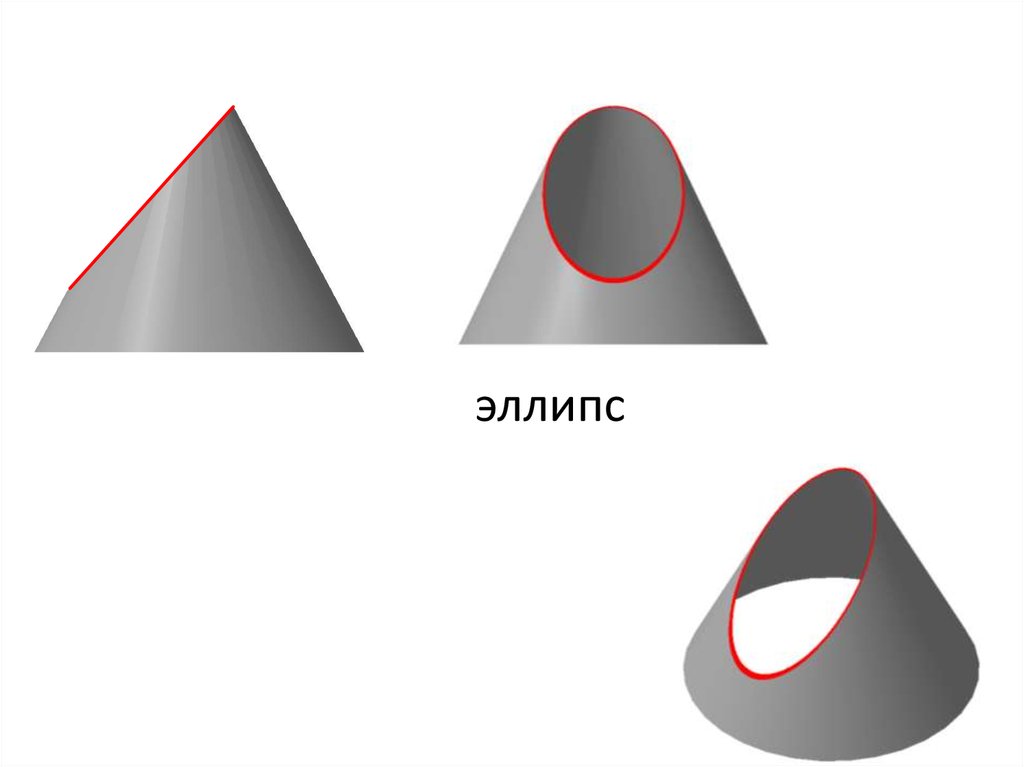
эллипс32.
33.
34.
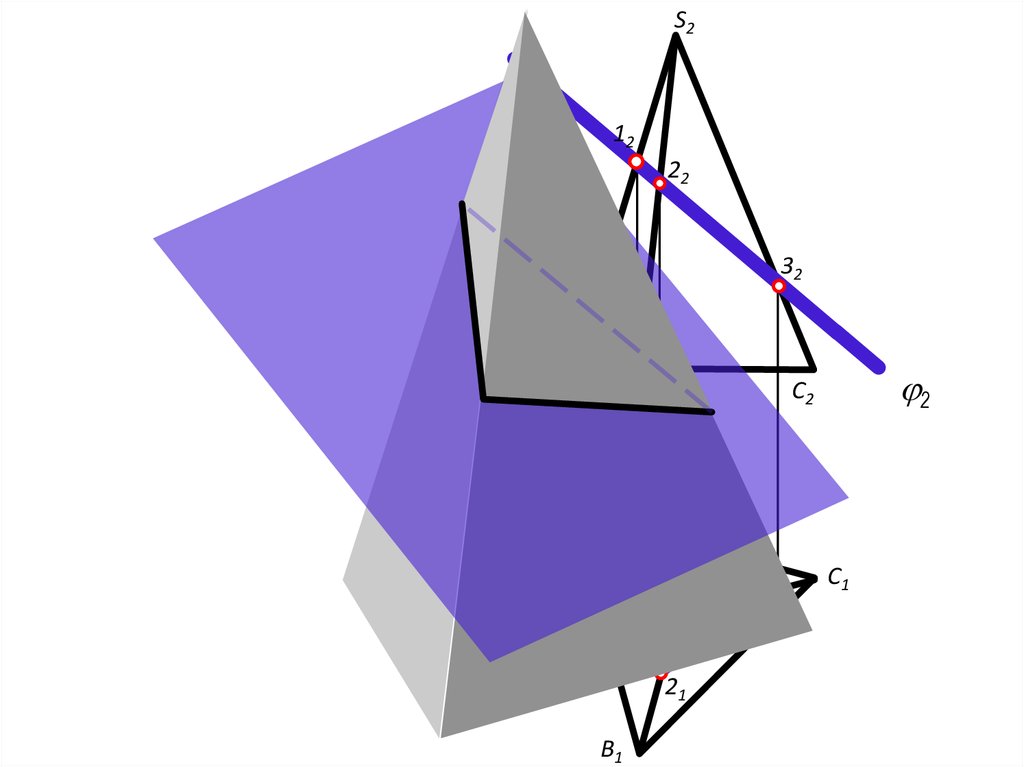
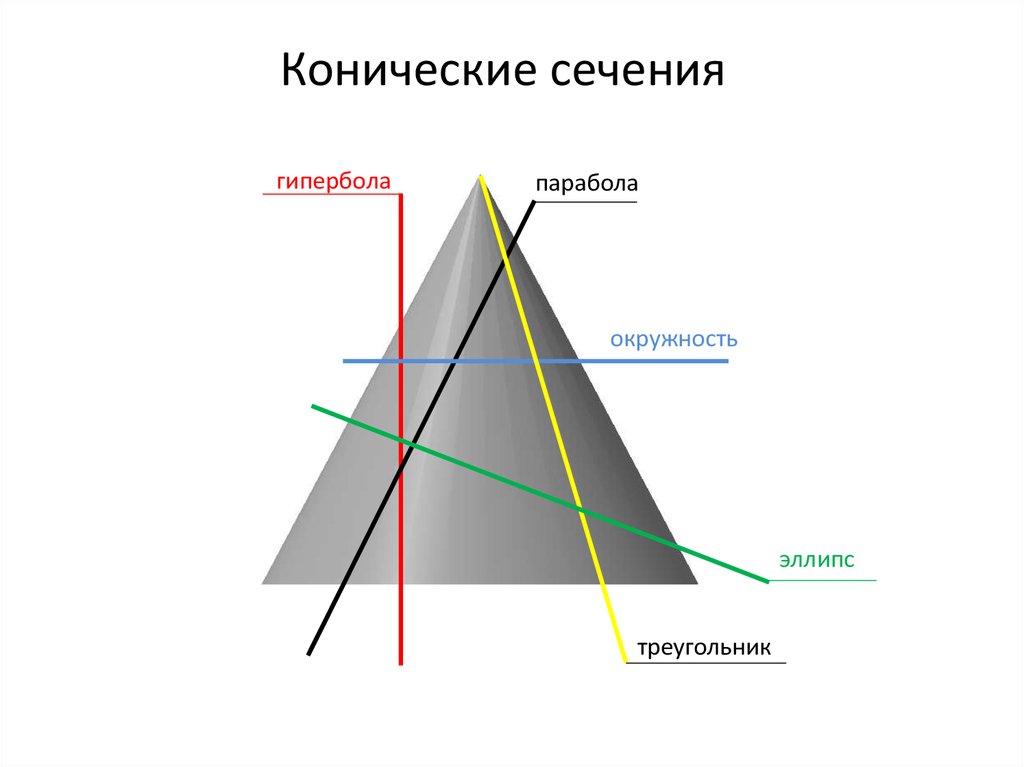
Конические сечениягипербола
парабола
окружность
эллипс
треугольник
35.
62 4252
72 32
22 82
12 1о2
2о2 8о2
3о2 7о2
4о2 6о2 5о2
7о1
8о1
6о1
81
71
61
51
11 1о1
5о1
41
2о1
21
31
3о1
4о1
36.
АлгоритмНа
поверхности обозначить ряд образующих.
Обязательно включить очерковые образующие с П1 и П2.
Обозначить
точки
пересечения
проецирующей
плоскости с образующими.
Перенести точки на другую плоскость проекций.
Соединить полученные проекции точек плавной кривой.
Показать видимость линии пересечения.
37.
52m2M
62 42
72 32
82 22
(12)
81
m1
71
M
61
11
51
21
41
31
n1
n2
38.
АлгоритмНа
поверхности обозначить ряд точек на следе
плоскости. Обязательно включить точки, лежащие на
экваторе и главном меридиане.
Перенести точки, лежащие на экваторе и главном
меридиане на другую плоскость проекций.
На поверхности обозначить ряд параллелей на П1 и П2.
Обозначить
точки
пересечения
проецирующей
плоскости с параллелями.
Перенести точки на другую плоскость проекций.
Соединить полученные проекции точек плавной кривой.
Показать видимость линии пересечения.
39. Пересечение прямой с гранными поверхностями
40.
41.
S2l2
А2
В2
2
С2
A1
l1
C1
B1
42.
Алгоритм построения точек пересеченияпрямой с поверхностью
l пл. ;
пл. с поверхностью линия d;
линия d l ( ) M, N.
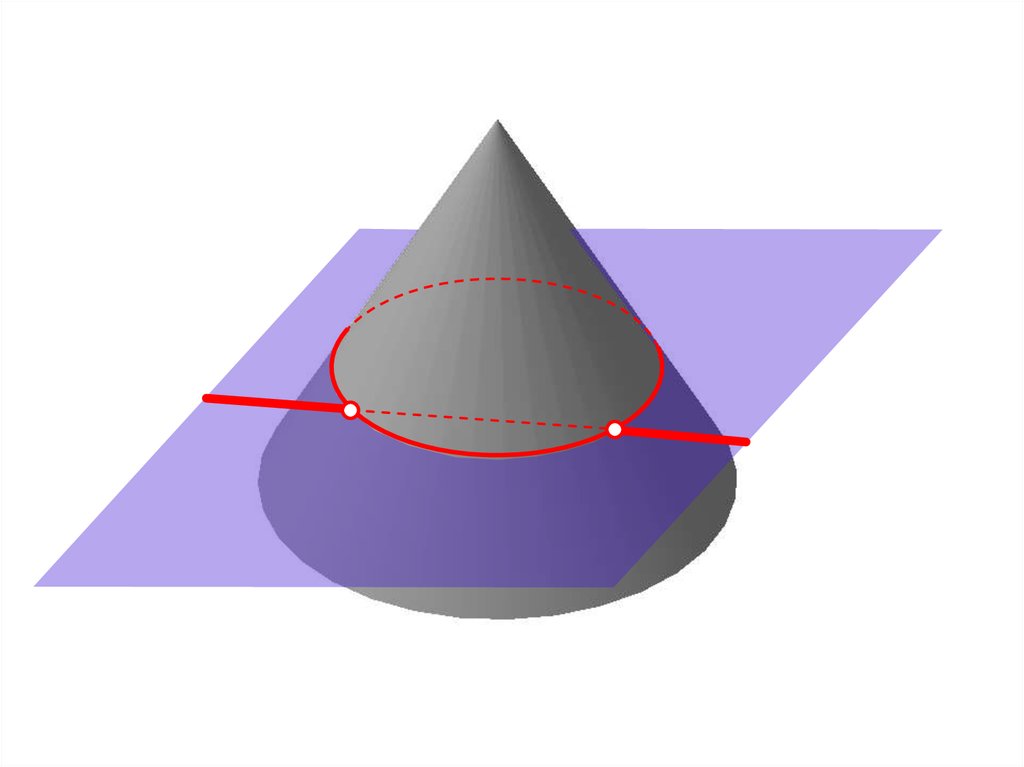
43. Пересечение прямой с линейчатой поверхностью
44.
45.
Алгоритм построения точек пересеченияпрямой с поверхностью
l пл. ;
пл. с поверхностью линия d;
линия d l ( ) M, N.
46.
47.
48.
49.
N2M2
l2
R
M1
N1
l1
2
50.
N2 M2l2
l1
N1
M1
2
51.
1M
3
N
2
5
6
4
52.
53.
1M
N
2
3
4
1
3
M
5
N
2
6
4
54.
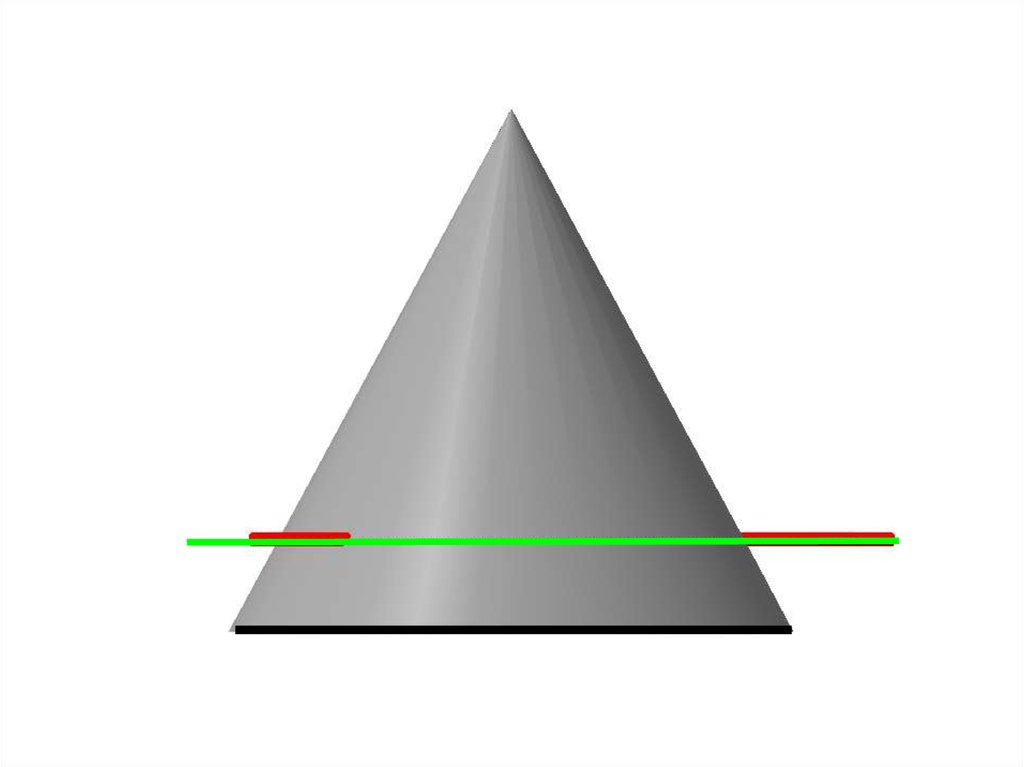
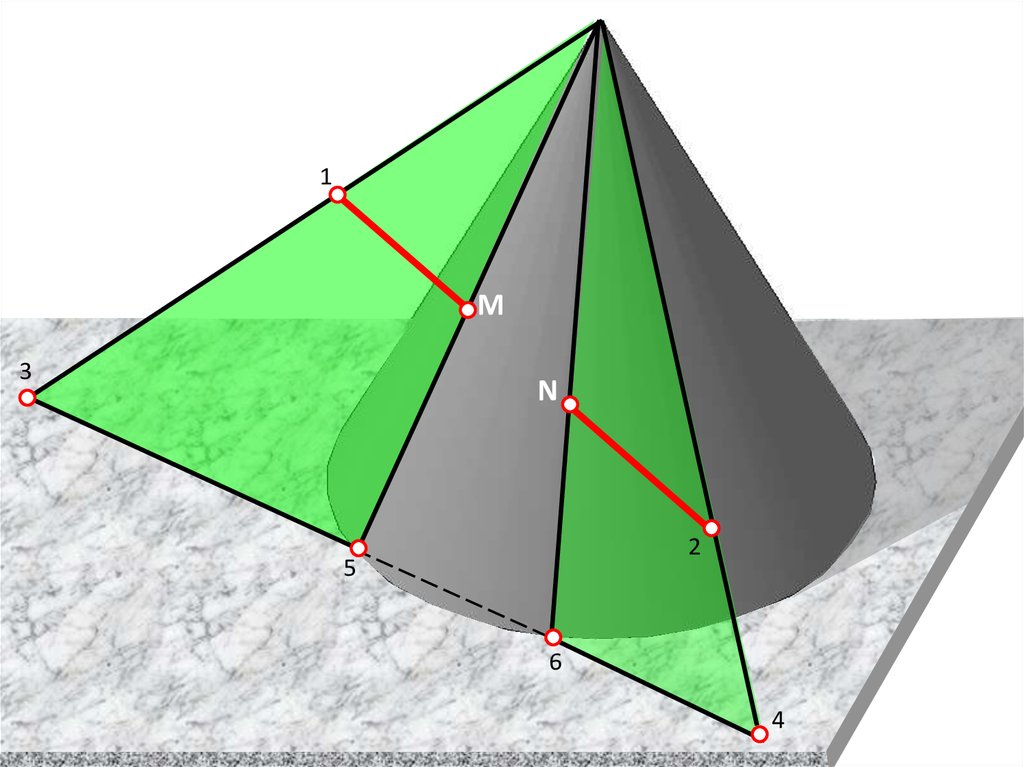
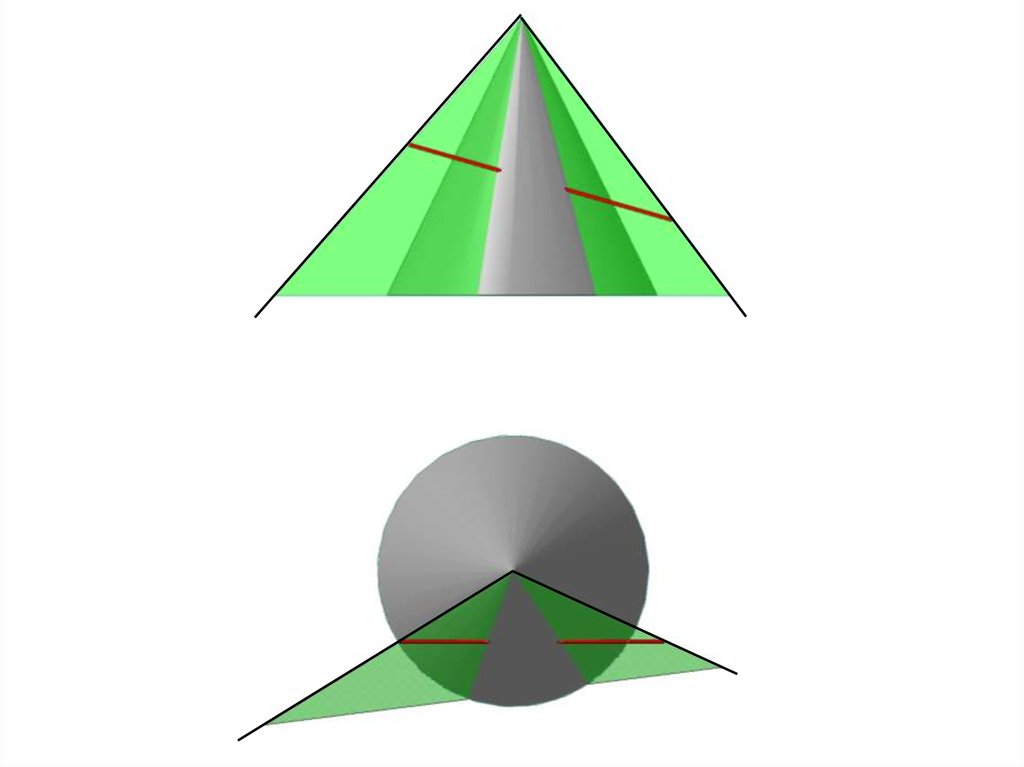
Алгоритм построения точек пересеченияпрямой ОП с конусом
Выбрать ( ) 1 и ( ) 2 на прямой.
Через вершину конуса и ( ) 1 и ( ) 2 провести лучи.
На пересечении лучей с плоскостью основания
конуса построить ( ) 3 и ( ) 4.
Построить линию 34 .
На пересечении линии с очерком основания конуса
построить ( ) 5 и ( ) 6 .
Построить образующие конуса из ( ) 5 и ( ) 6 .
На пересечении образующих с прямой построить
( ) М и ( ) N.
55.
56.
57.
l2х12
l1
1
58.
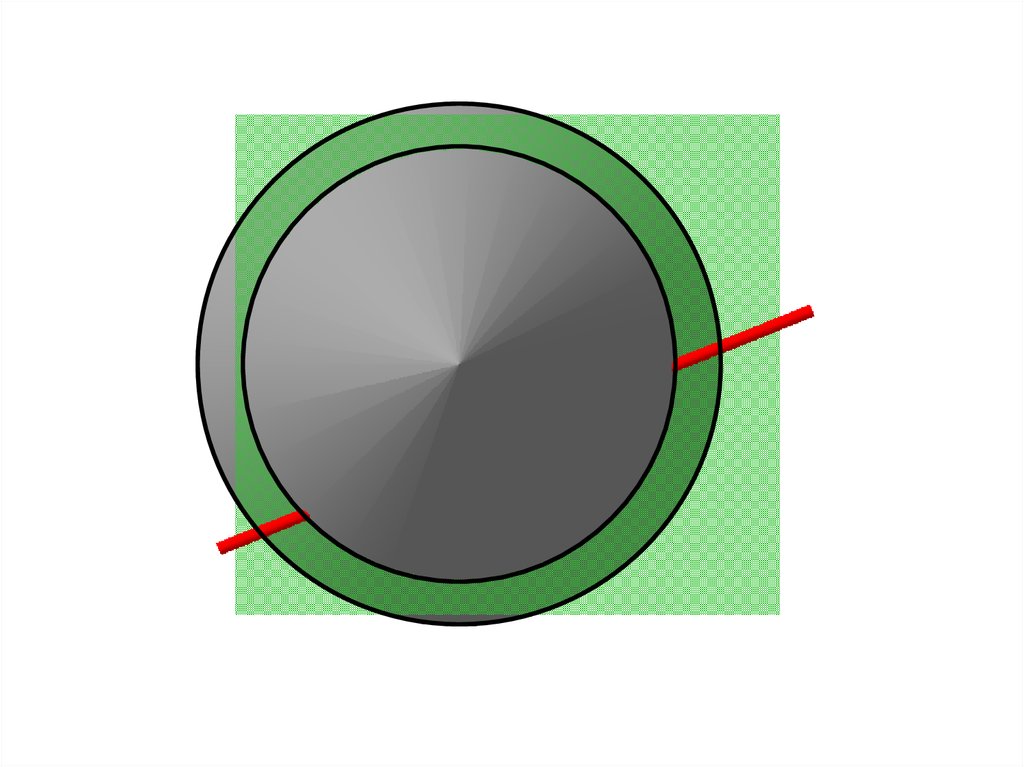
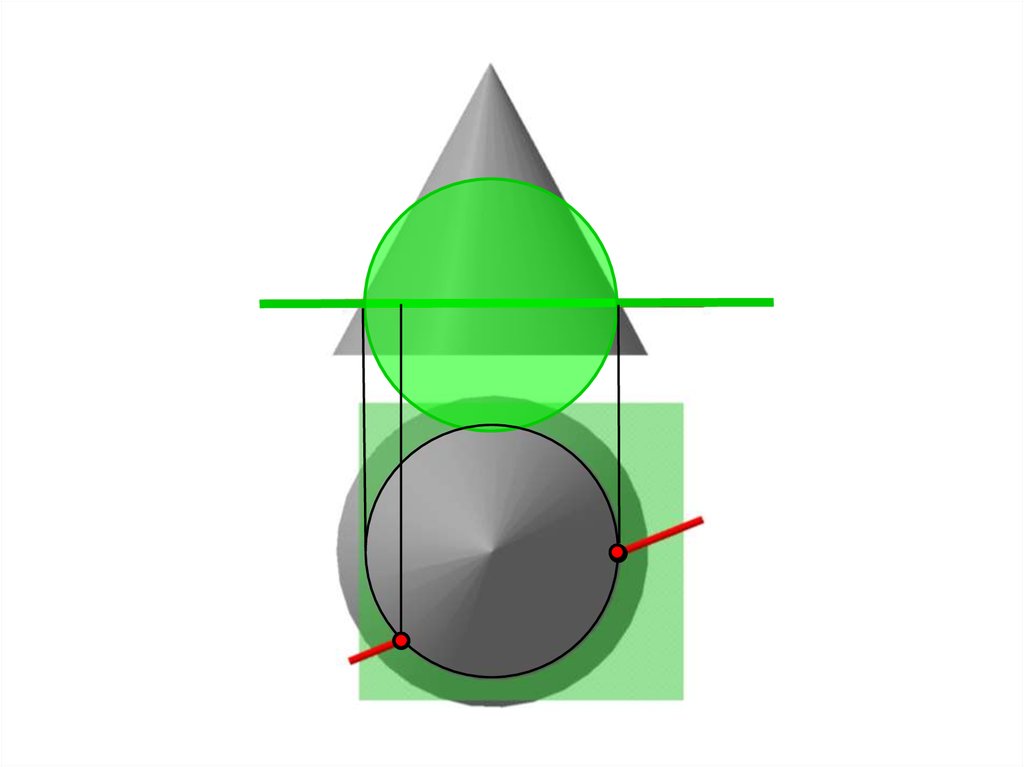
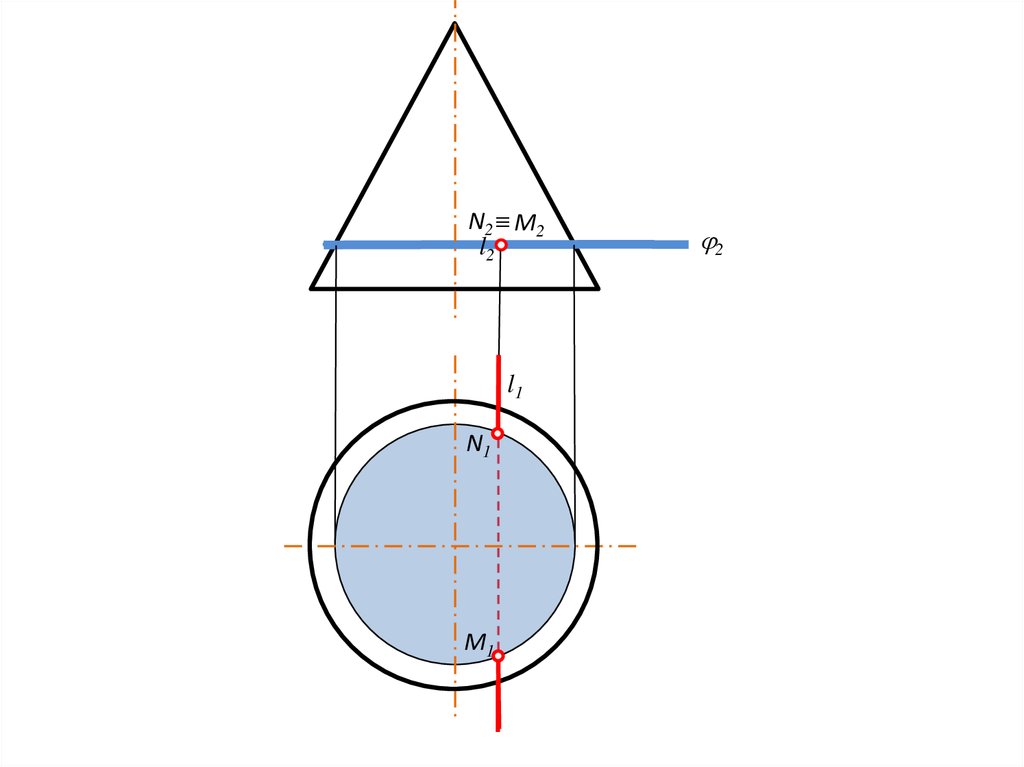
Алгоритм построения точек пересеченияпрямой ОП со сферой
Заключить прямую l в проецирующую плоскость .
Ввести дополнительную плоскость проекций Пi+1 .
На пл. Пi+1 построить центр сферы О и прямую l.
Из центра Оi+1 построить сечение сферы плоскостью
(окружность).
Обозначить точки пересечения проекций сечения сферы и прямой
на пл. Пi+1 .
Точки перенести с плоскости Пi+1 на плоскости проекций Пi , П1, П2.
59.
(M2)m2
N2
Х
m1
M1
N1
2



























 Инженерная графика
Инженерная графика








