Простая регрессионная модель

1.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y b1 b 2 X
b1
X1
X2
X3
X4
X
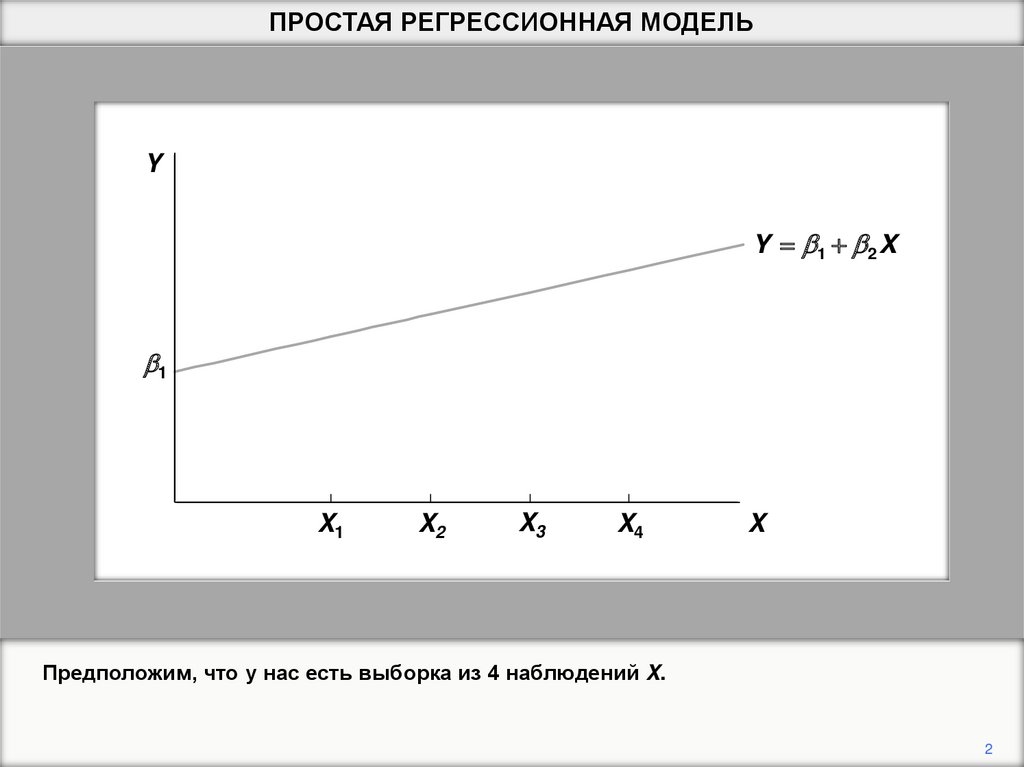
Предположим, что переменная Y является линейной функцией другой переменной X, с
неизвестными параметрами b1 and b2, которые мы хотим оценить.
1

2.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y b1 b 2 X
b1
X1
X2
X3
X4
X
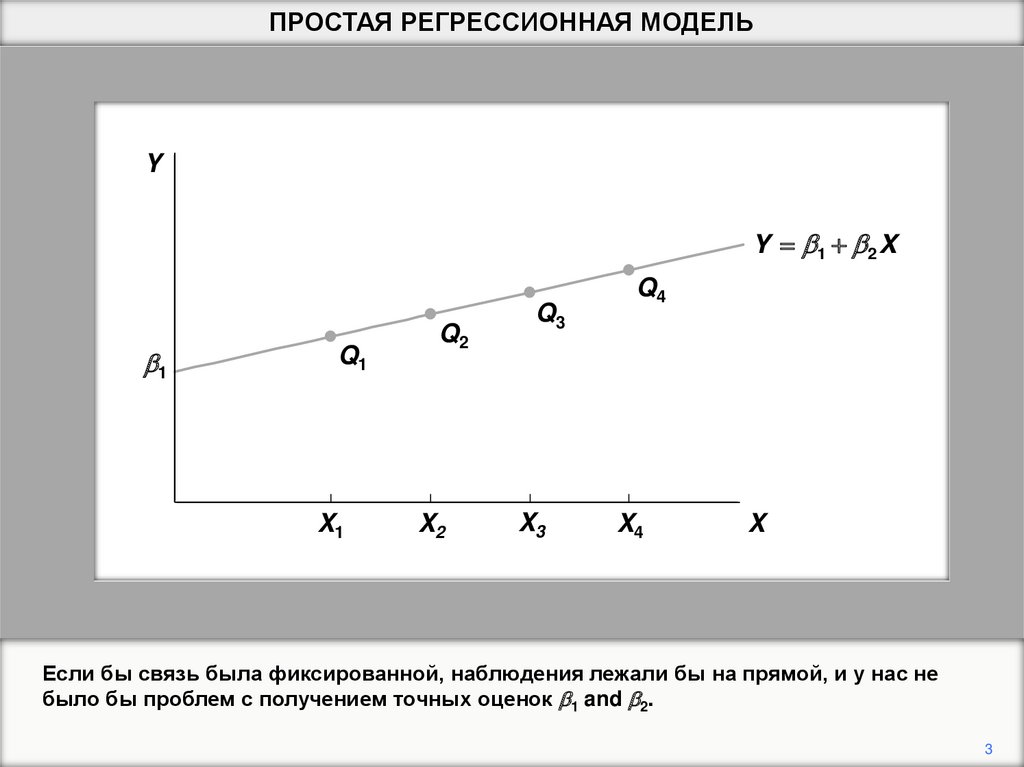
Предположим, что у нас есть выборка из 4 наблюдений X.
2

3.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y b1 b 2 X
b1
Q1
X1
Q2
X2
Q3
X3
Q4
X4
X
Если бы связь была фиксированной, наблюдения лежали бы на прямой, и у нас не
было бы проблем с получением точных оценок b1 and b2.
3

4.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Y b1 b 2 X
P1
b1
Q1
X1
Q2
P2
X2
Q3
Q4
P3
X3
X4
X
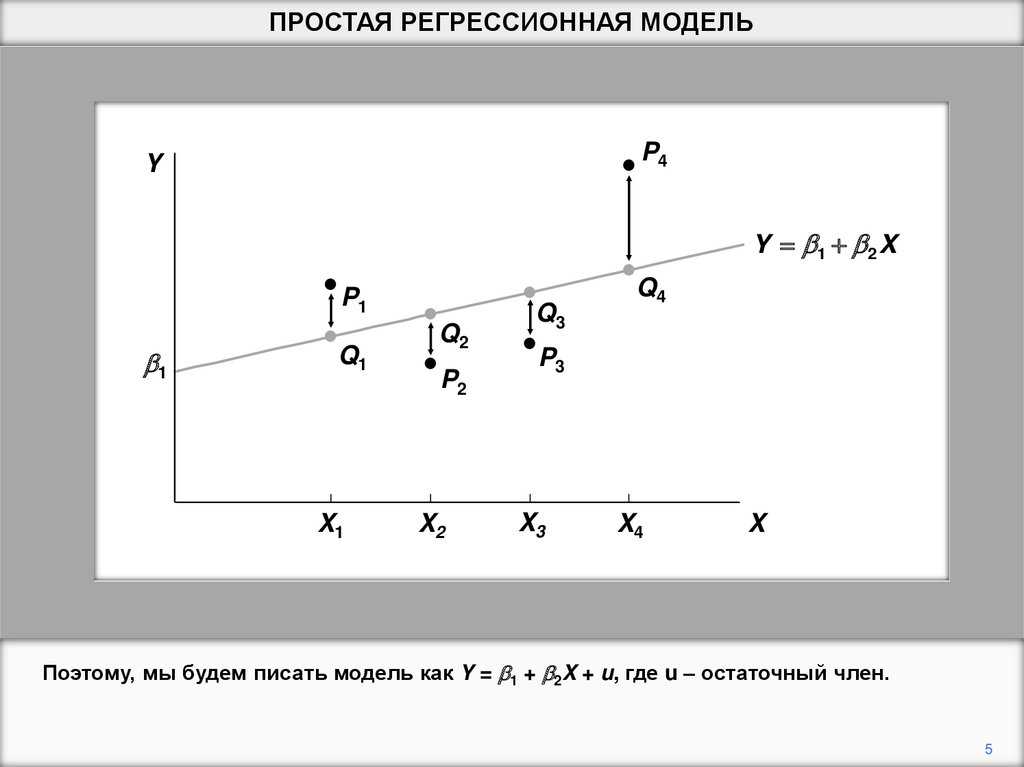
На практике большинство экономических показателей не являются точными, а
фактические значенияY отличаются от значений, лежащих на прямой.
4

5.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Y b1 b 2 X
P1
b1
Q1
X1
Q2
P2
X2
Q3
Q4
P3
X3
X4
X
Поэтому, мы будем писать модель как Y = b1 + b2X + u, где u – остаточный член.
5

6.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Y b1 b 2 X
u1 P1
b1
Q1
b1 b 2 X 1
X1
Q2
P2
X2
Q3
Q4
P3
u = остаточный член
X3
X4
X
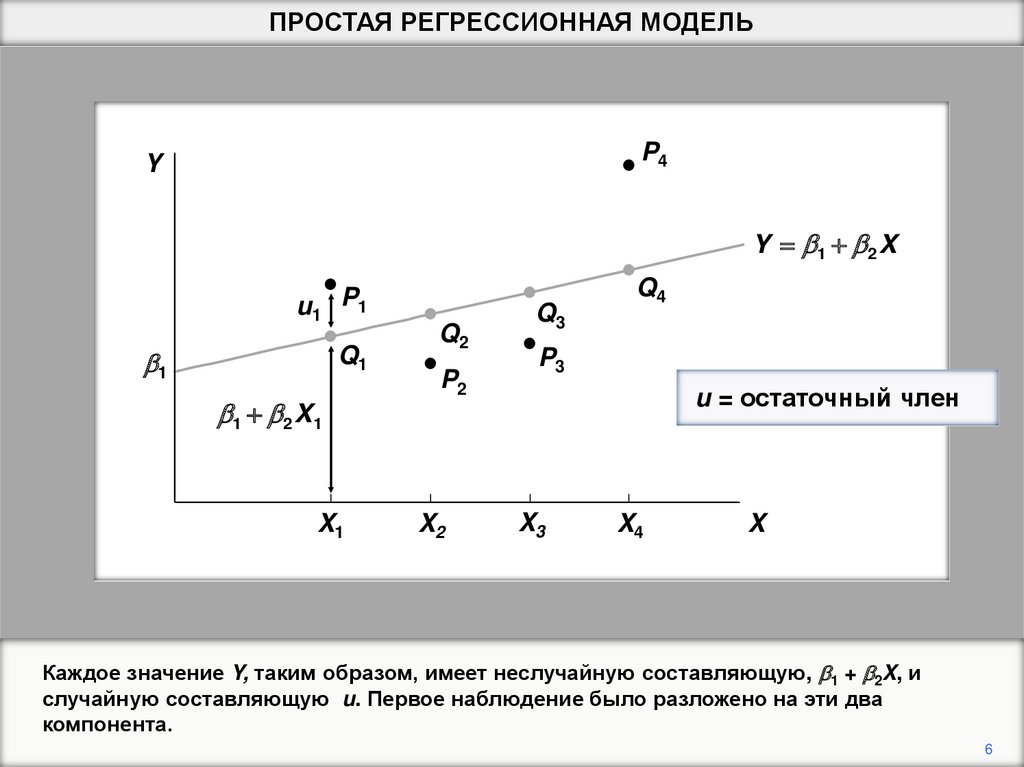
Каждое значение Y, таким образом, имеет неслучайную составляющую, b1 + b2X, и
случайную составляющую u. Первое наблюдение было разложено на эти два
компонента.
6

7.

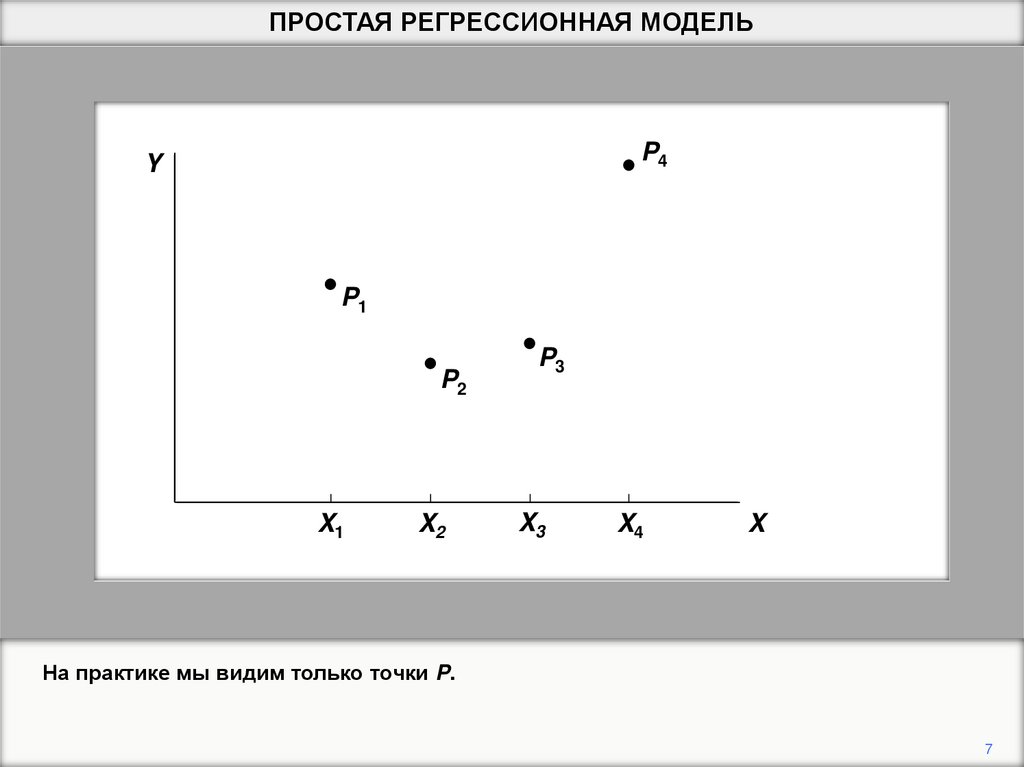
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
P1
P2
X1
X2
P3
X3
X4
X
На практике мы видим только точки P.
7

8.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Yˆ b1 b2 X
P1
P2
b1
X1
X2
P3
X3
X4
X
Очевидно, что мы можем использовать точки P, чтобы нарисовать линию, которая
является приближением к прямой Y = b1 + b2X.
^
Мы напишем эту прямую в виде Y = b1 + b2X, где b1 - оценка b1 , а b2 - оценка b2.
8

9.

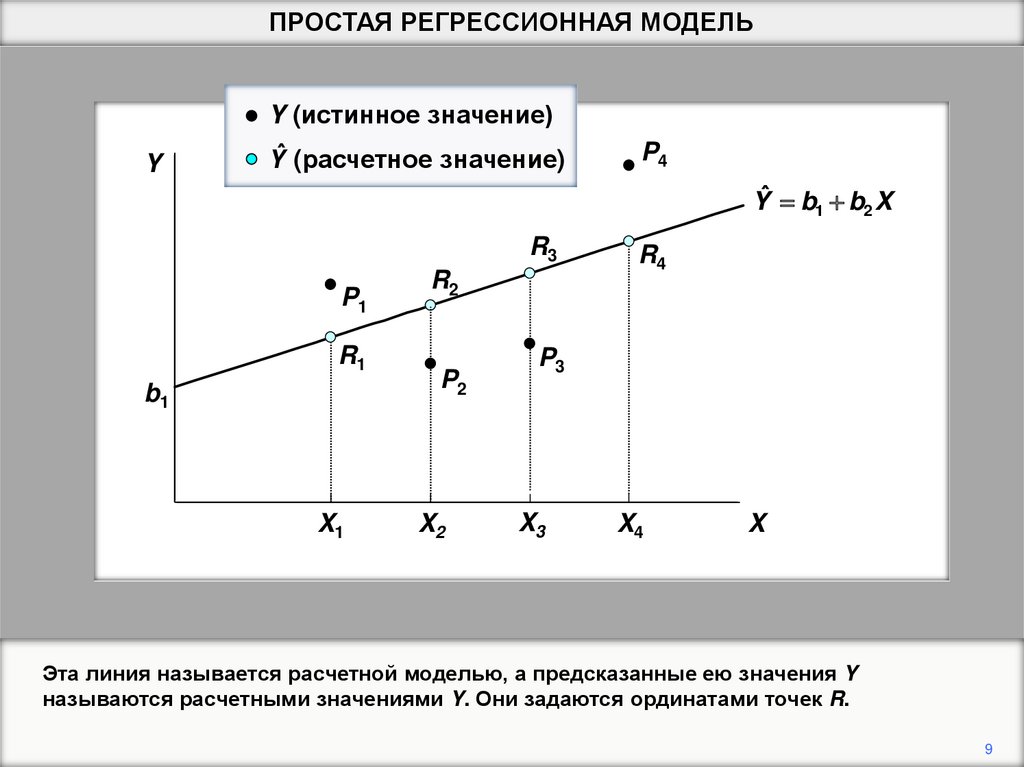
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
R3
P1
R1
b1
X1
R2
P2
X2
R4
P3
X3
X4
X
Эта линия называется расчетной моделью, а предсказанные ею значения Y
называются расчетными значениями Y. Они задаются ординатами точек R.
9

10.

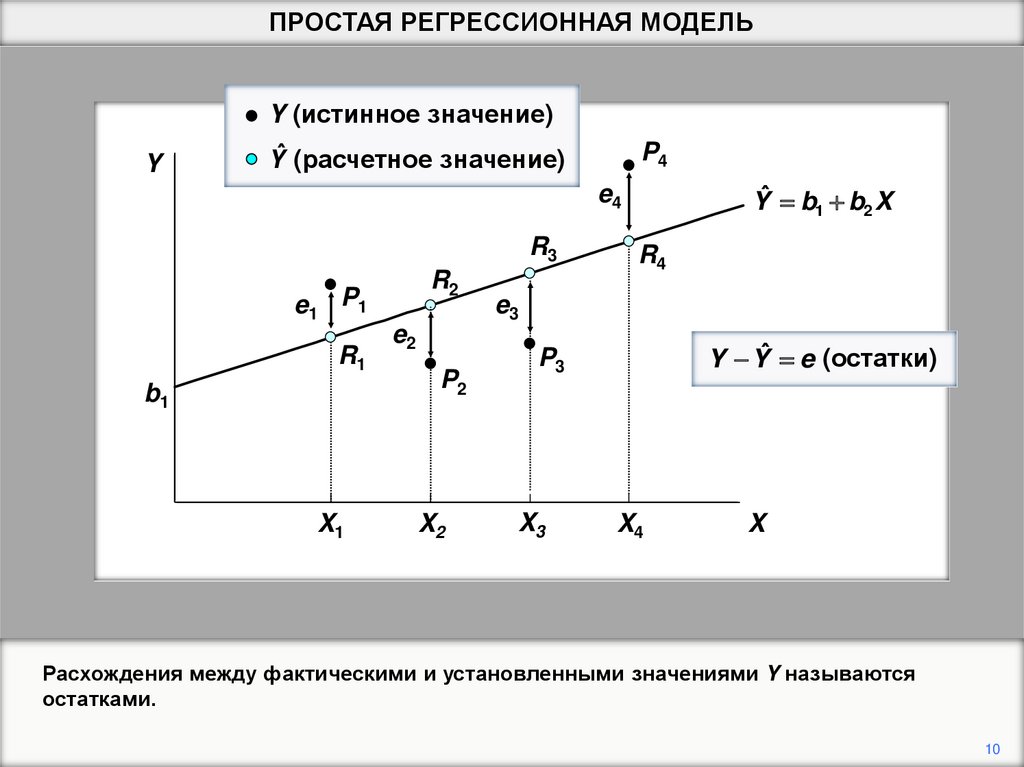
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
e4
R3
e1
R2
P1
R1
b1
X1
e2
P2
X2
R4
e3
Y Yˆ e (остатки)
P3
X3
X4
X
Расхождения между фактическими и установленными значениями Y называются
остатками.
10

11.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
R3
P1
b1
R1
b1
X1
R2
P2
X2
R4
Y b1 b 2 X
P3
X3
X4
X
Обратите внимание, что значения остатков не совпадают с величиной остаточного
члена. На диаграмме показаны истинные неизвестные отношения, а также расчетная
линия.
11

12.

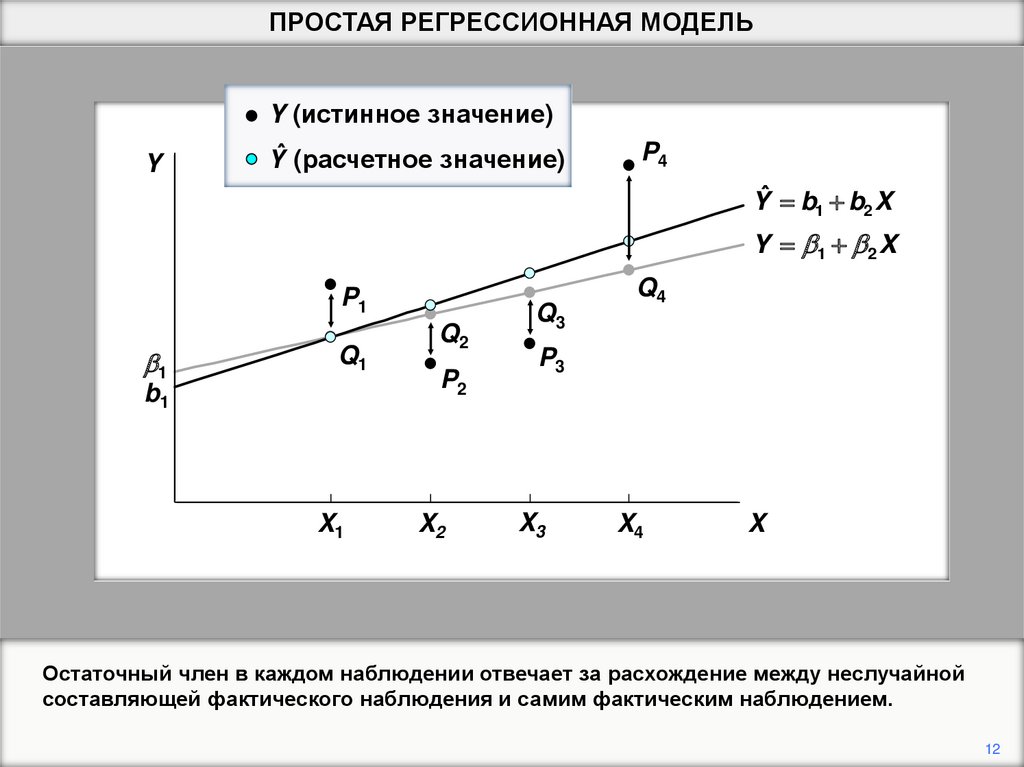
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
Y b1 b 2 X
P1
b1
Q1
b1
X1
Q2
P2
X2
Q3
Q4
P3
X3
X4
X
Остаточный член в каждом наблюдении отвечает за расхождение между неслучайной
составляющей фактического наблюдения и самим фактическим наблюдением.
12

13.

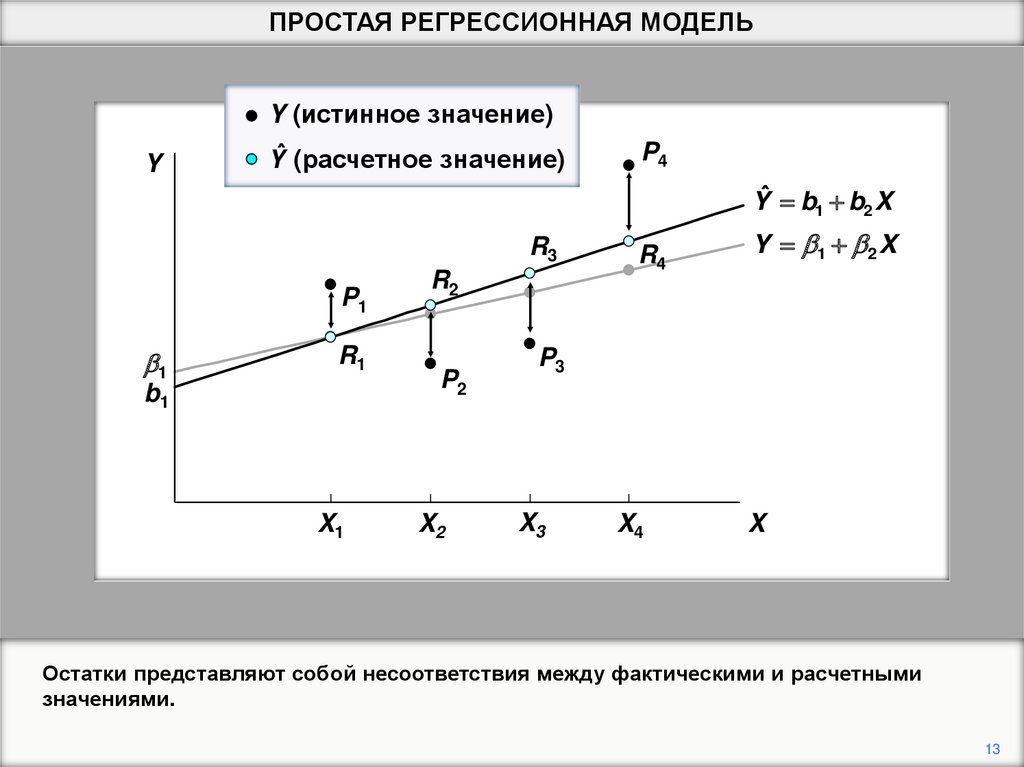
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
R3
P1
b1
R1
b1
X1
R2
P2
X2
R4
Y b1 b 2 X
P3
X3
X4
X
Остатки представляют собой несоответствия между фактическими и расчетными
значениями.
13

14.

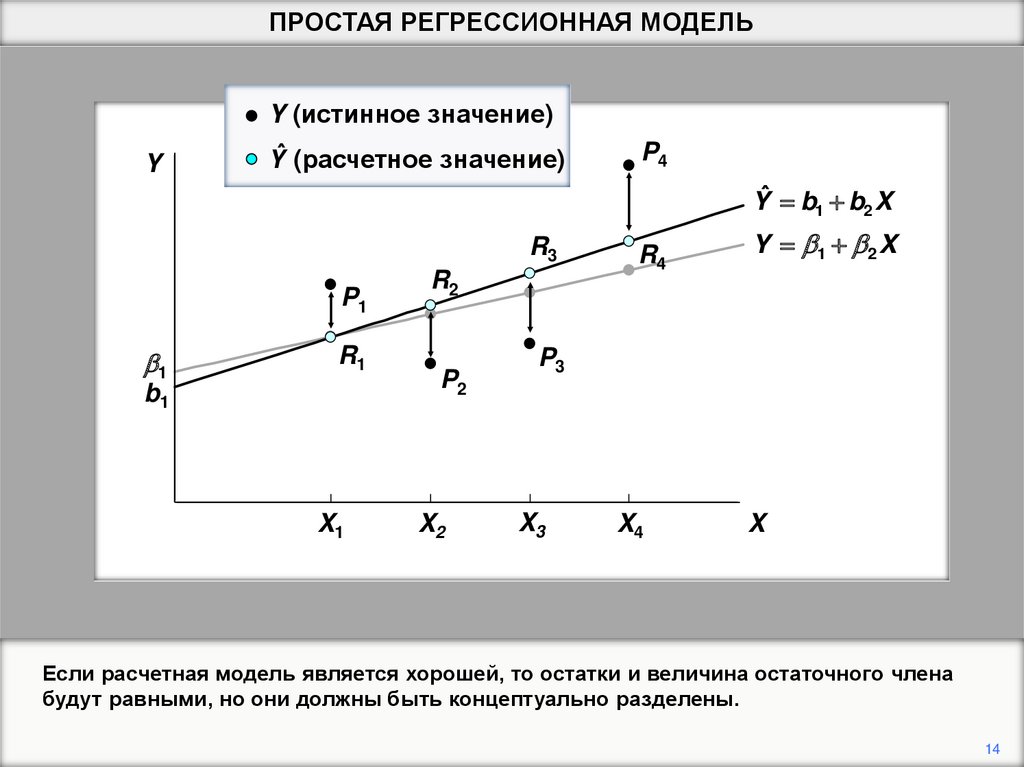
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
R3
P1
b1
R1
b1
X1
R2
P2
X2
R4
Y b1 b 2 X
P3
X3
X4
X
Если расчетная модель является хорошей, то остатки и величина остаточного члена
будут равными, но они должны быть концептуально разделены.
14

15.

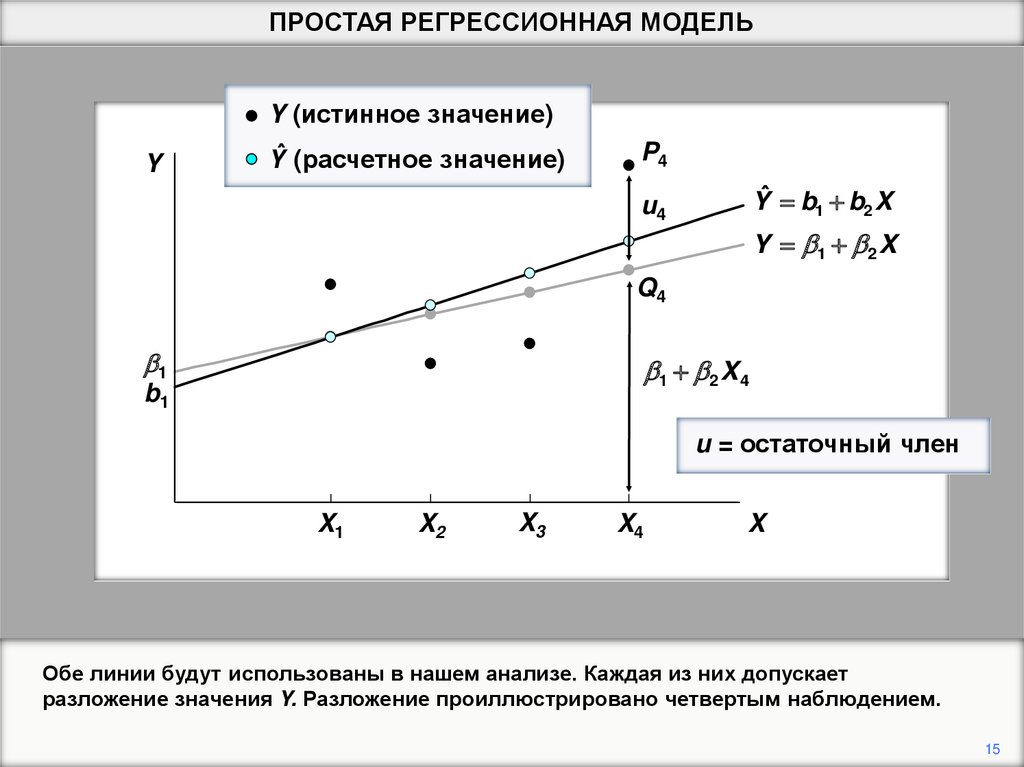
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
u4
Y b1 b 2 X
Q4
b1
b1 b 2 X 4
b1
u = остаточный член
X1
X2
X3
X4
X
Обе линии будут использованы в нашем анализе. Каждая из них допускает
разложение значения Y. Разложение проиллюстрировано четвертым наблюдением.
15

16.

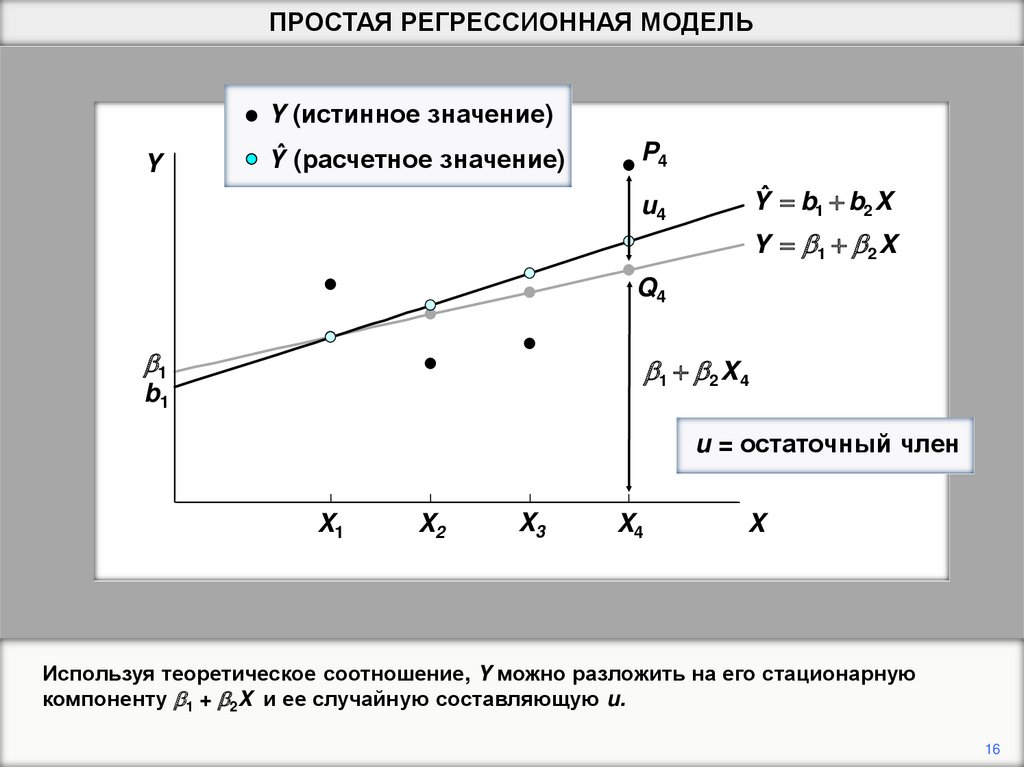
ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
u4
Y b1 b 2 X
Q4
b1
b1 b 2 X 4
b1
u = остаточный член
X1
X2
X3
X4
X
Используя теоретическое соотношение, Y можно разложить на его стационарную
компоненту b1 + b2X и ее случайную составляющую u.
16

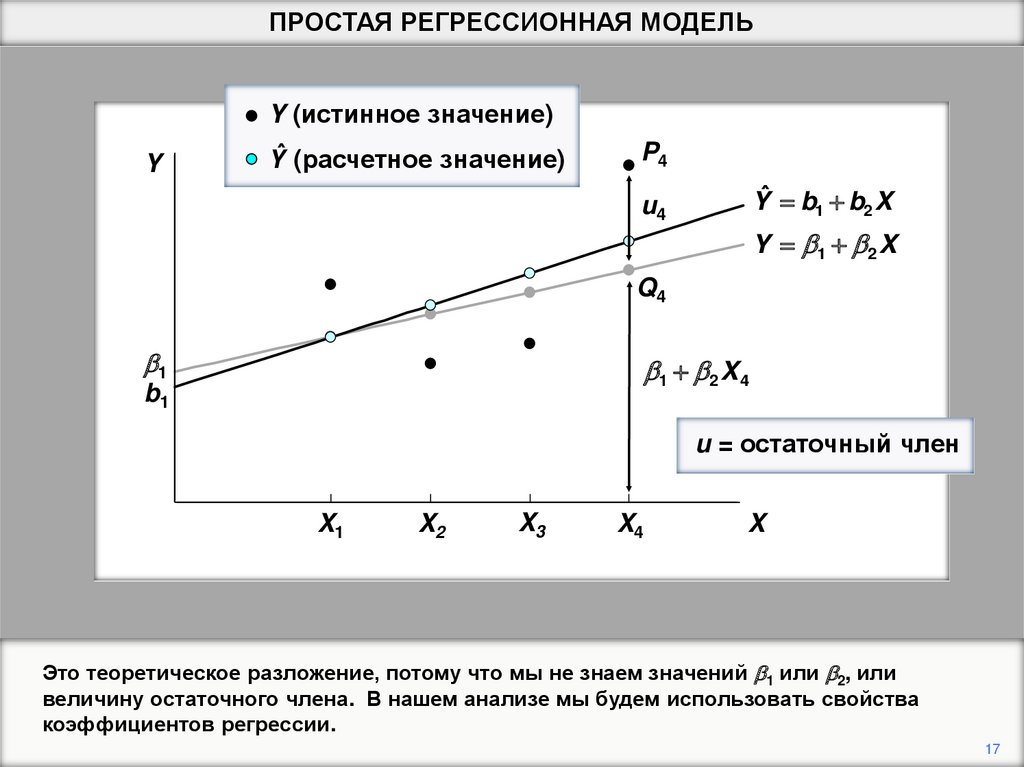
17.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
P4
Yˆ b1 b2 X
u4
Y b1 b 2 X
Q4
b1
b1 b 2 X 4
b1
u = остаточный член
X1
X2
X3
X4
X
Это теоретическое разложение, потому что мы не знаем значений b1 или b2, или
величину остаточного члена. В нашем анализе мы будем использовать свойства
коэффициентов регрессии.
17

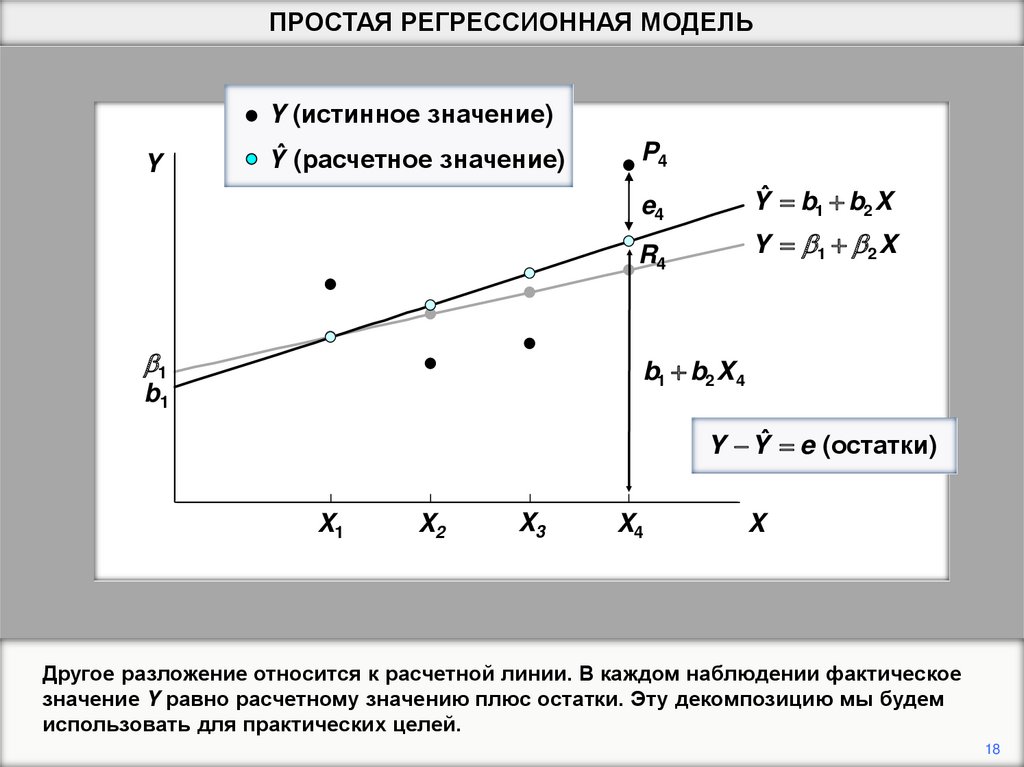
18.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Y
Y (истинное значение)
Yˆ (расчетное значение)
b1
P4
e4
Yˆ b1 b2 X
R4
Y b1 b 2 X
b1 b2 X 4
b1
Y Yˆ e (остатки)
X1
X2
X3
X4
X
Другое разложение относится к расчетной линии. В каждом наблюдении фактическое
значение Y равно расчетному значению плюс остатки. Эту декомпозицию мы будем
использовать для практических целей.
18

19.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Критерий наименьших квадратов:
Минимизировать RSS (сумма квадратов остатков), где
n
RSS ei2 e12 ... en2
i 1
Начнем с того, что мы построим линию, чтобы свести к минимуму сумму квадратов
остатков RSS. Это есть критерий наименьших квадратов.
19

20.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Критерий наименьших квадратов:
Минимизировать RSS (сумма квадратов остатков), где
n
RSS ei2 e12 ... en2
i 1
Почему бы не минимизировать
n
e
i 1
i
e1 ... en
Почему квадраты остатков? Почему бы не просто свести к минимуму сумму остатков?
20

21.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Y
P1
P2
X1
X2
P3
X3
X4
X
Ответ заключается в том, что вы получите, идеальную форму, строя горизонтальную
линию через среднее значение Y. Сумма остатков будет равна нулю.
21

22.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Y
P1
P2
X1
X2
P3
X3
X4
X
Поэтому вы должны предотвратить взаимоисключение отрицательных и
положительных остатков, и один из способов сделать это - использовать квадраты
остатков.
22

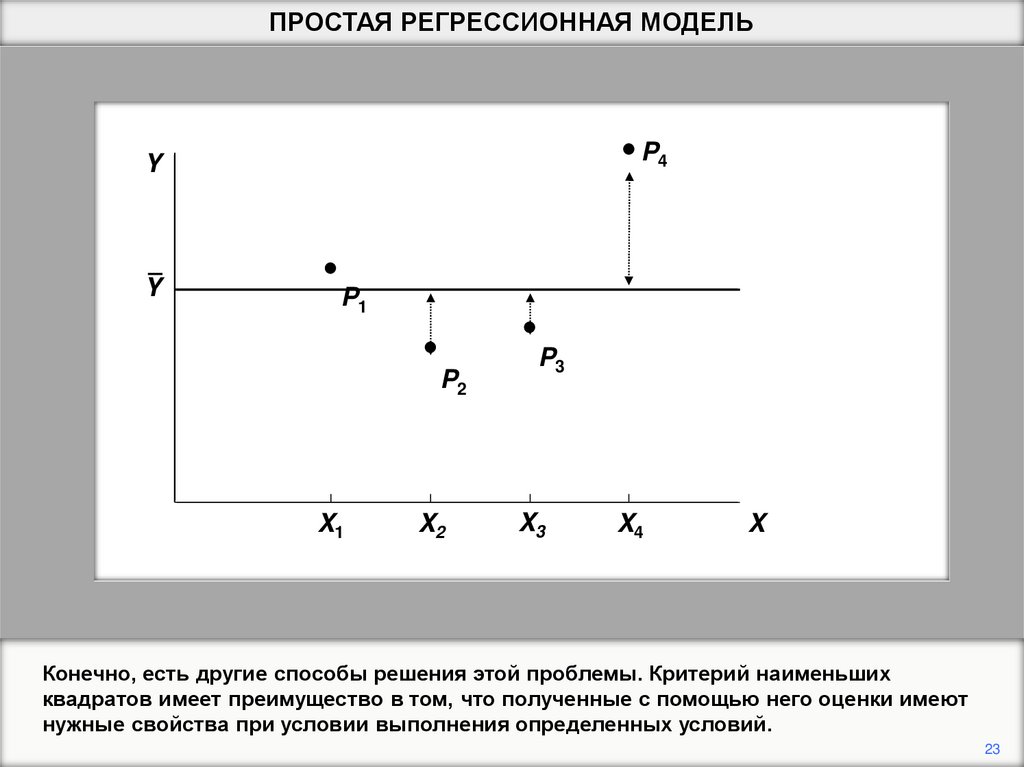
23.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Y
P1
P2
X1
X2
P3
X3
X4
X
Конечно, есть другие способы решения этой проблемы. Критерий наименьших
квадратов имеет преимущество в том, что полученные с помощью него оценки имеют
нужные свойства при условии выполнения определенных условий.
23

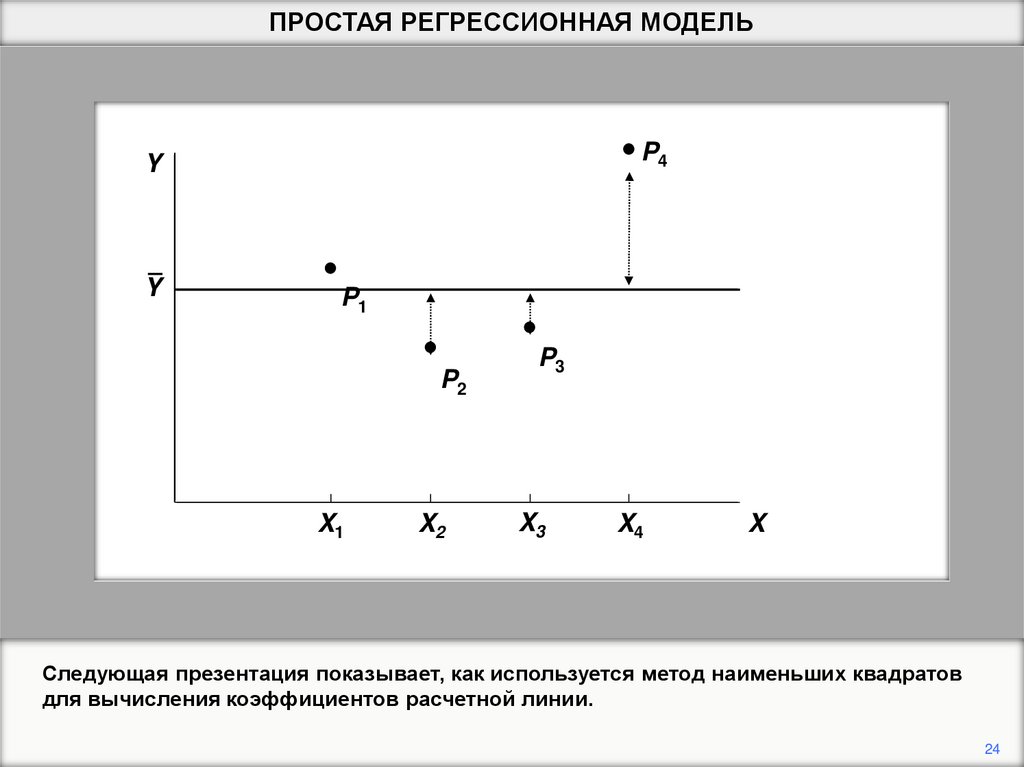
24.

ПРОСТАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
P4
Y
Y
P1
P2
X1
X2
P3
X3
X4
X
Следующая презентация показывает, как используется метод наименьших квадратов
для вычисления коэффициентов расчетной линии.
24