Похожие презентации:
Перехід між кутами у правильних пірамідах
1.
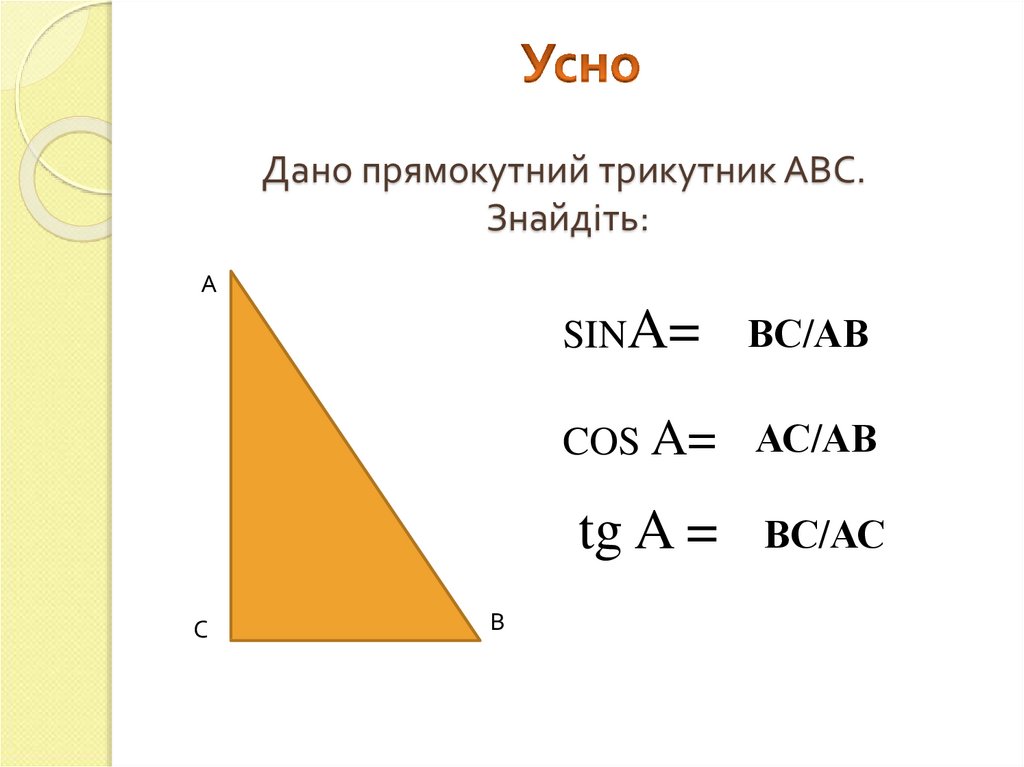
2. Усно Дано прямокутний трикутник АВС. Знайдіть:
Дано прямокутний трикутник АВС.Знайдіть:
А
SINA=
ВС/АВ
COS A= АС/АВ
tg A =
С
В
ВС/АС
3.
SD
А
K
О
В
С
4.
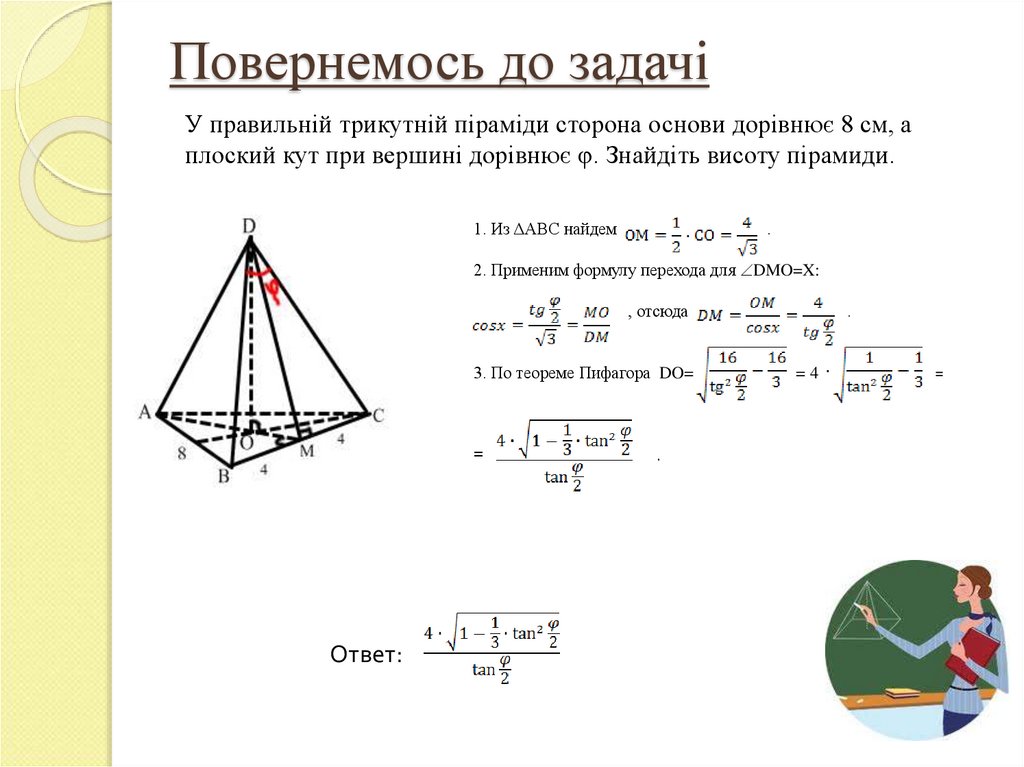
У правильній трикутній піраміди сторона основи дорівнює 8 см, аплоский кут при вершині дорівнює φ. Знайдіть висоту пірамиди.
Решение:
1. Из ΔDМВ знайдемо бічне ребро
2. З ΔCDO шукаємо висоту піраміди DO=
=H=
,
де ОС – радіус кола, описаного навколо основи
3. За теоремою синусів
4.
=4
, ОС=
=
=
=
Відповідь:
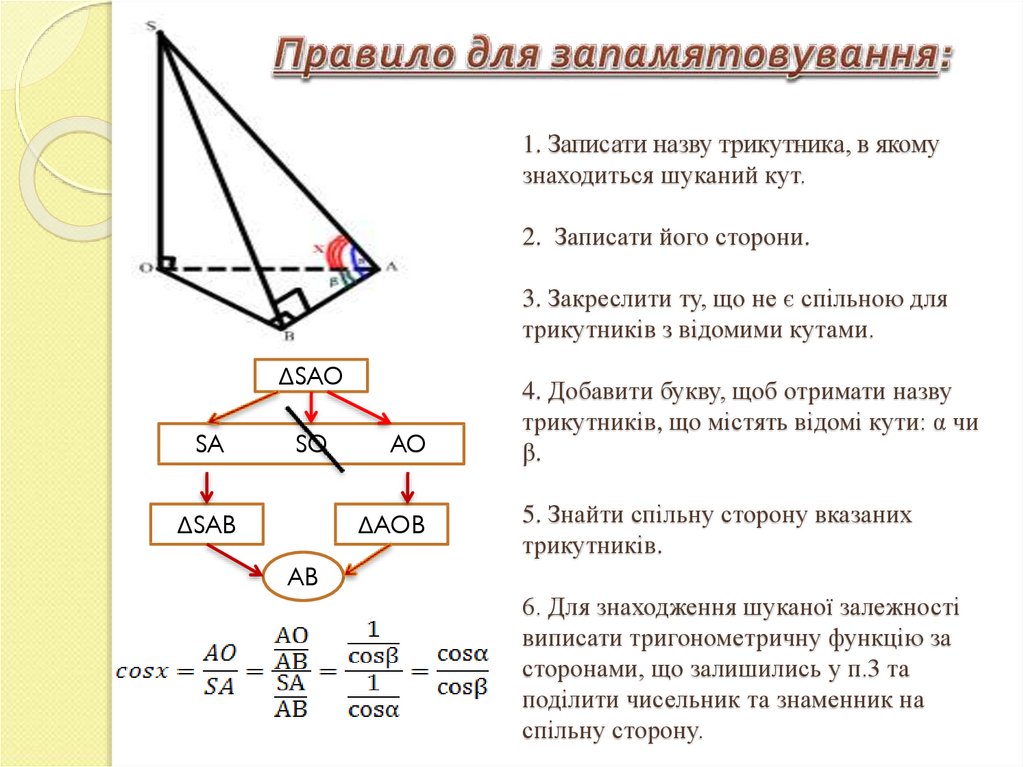
5. 1. Записати назву трикутника, в якому знаходиться шуканий кут. 2. Записати його сторони. 3. Закреслити ту, що не є спільною для
трикутників з відомими кутами.ΔSAO
SA
SO
ΔSAB
AO
ΔAOB
4. Добавити букву, щоб отримати назву
трикутників, що містять відомі кути: α чи
β.
5. Знайти спільну сторону вказаних
трикутників.
AB
6. Для знаходження шуканої залежності
виписати тригонометричну функцію за
сторонами, що залишились у п.3 та
поділити чисельник та знаменник на
спільну сторону.
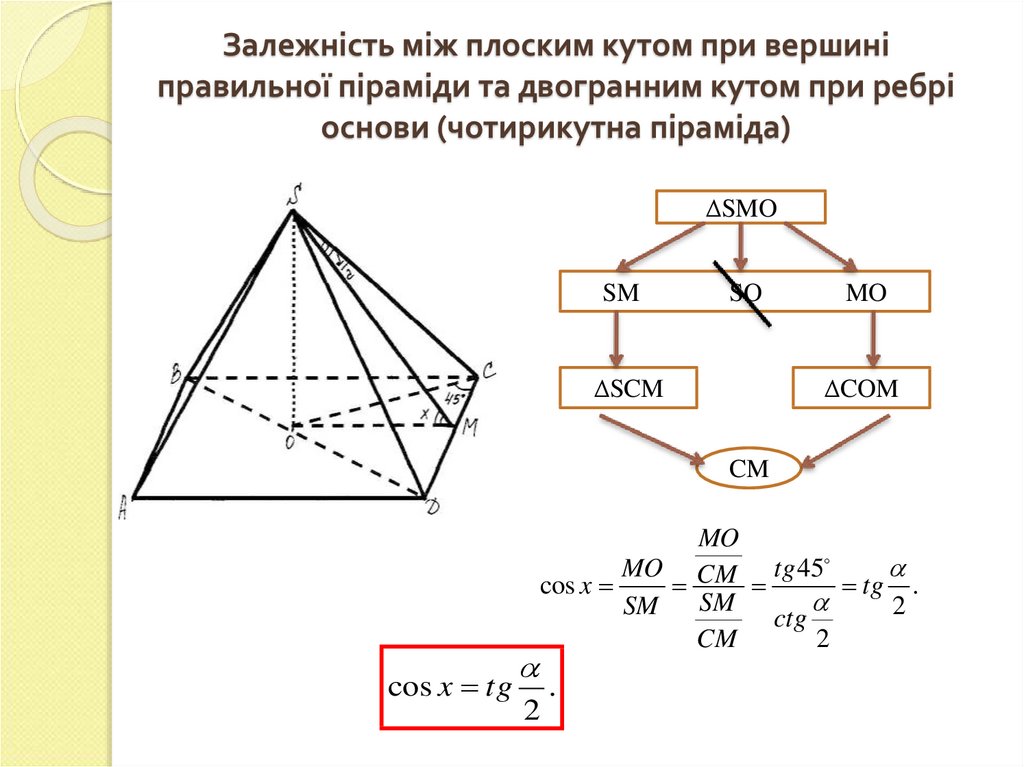
6. Залежність між плоским кутом при вершині правильної піраміди та двогранним кутом при ребрі основи (чотирикутна піраміда)
ΔSMOSM
SO
ΔSCM
MO
ΔCOM
CM
cos x tg
MO
MO CM tg 45
cos x
tg .
SM
SM
2
ctg
CM
2
2
.
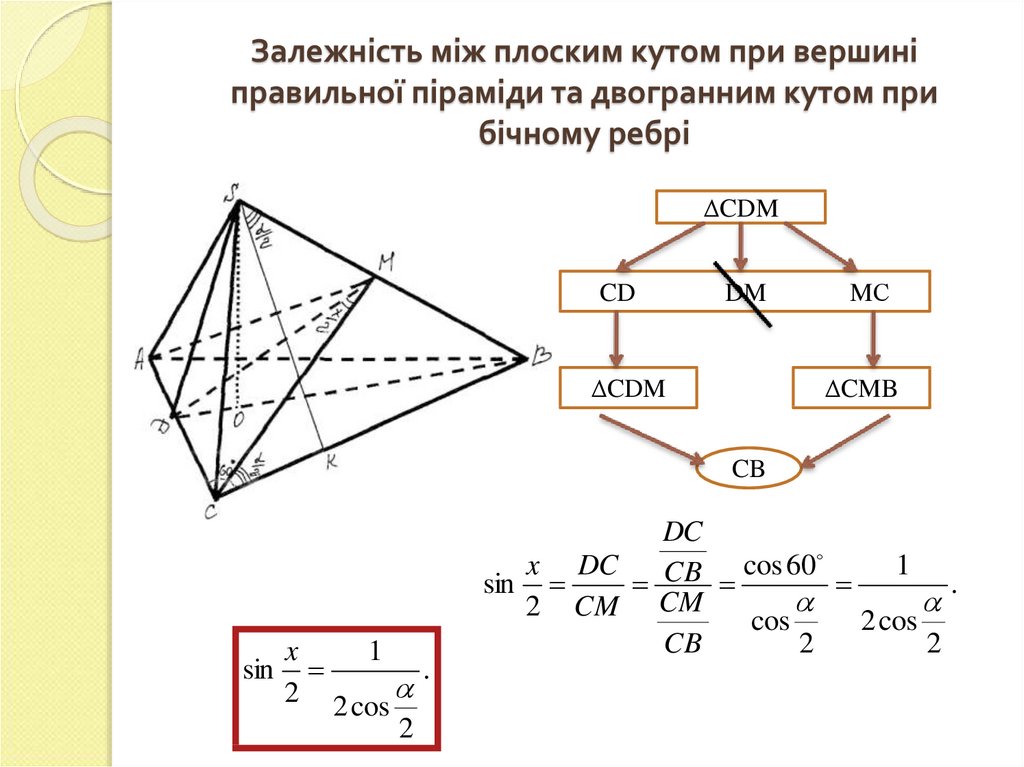
7. Залежність між плоским кутом при вершині правильної піраміди та двогранним кутом при бічному ребрі
ΔCDMCD
DM
ΔCDM
MС
ΔCMB
CB
x
1
sin
.
2 2 cos
2
DC
x DC
cos
60
1
CB
sin
.
CM
2 CM
cos
2 cos
CB
2
2
8. Повернемось до задачі
У правильній трикутній піраміди сторона основи дорівнює 8 см, аплоский кут при вершині дорівнює φ. Знайдіть висоту пірамиди.
1. Из ΔАВС найдем
.
2. Применим формулу перехода для DMO=X:
, отсюда
3. По теореме Пифагора DO=
=
Ответ:
.
.
=4
=
9.
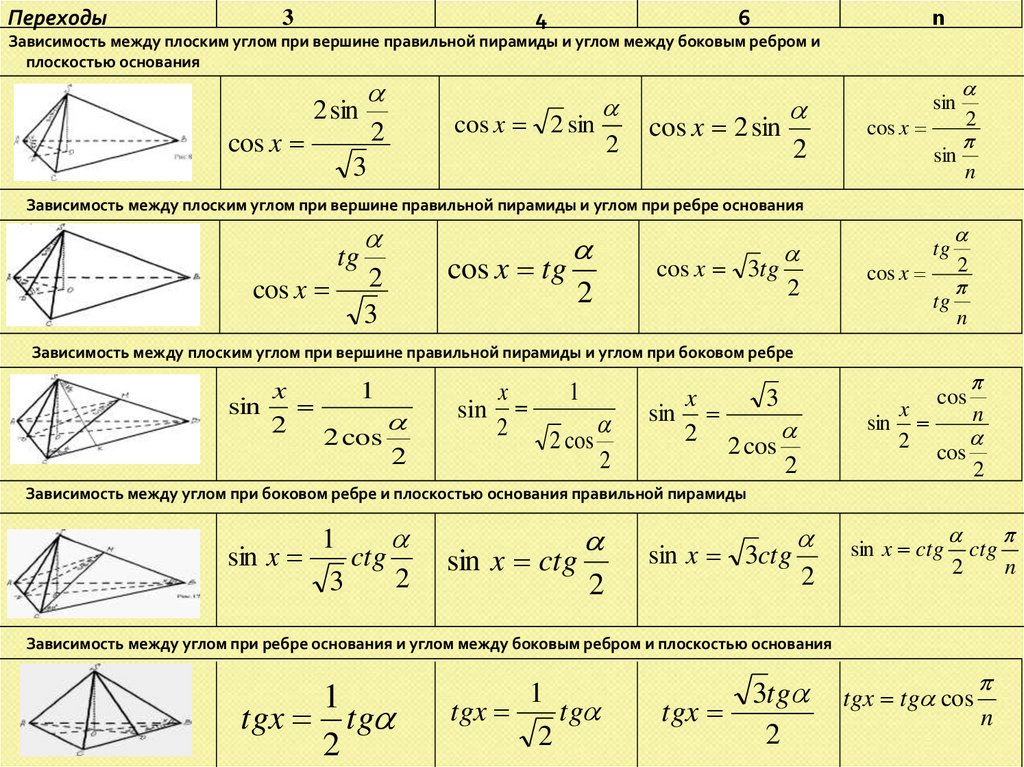
Переходы4
3
n
6
Зависимость между плоским углом при вершине правильной пирамиды и углом между боковым ребром и
плоскостью основания
cos x
2 sin
cos x 2 sin
2
3
2
cos x 2 sin
cos x
2
sin
2
sin
n
Зависимость между плоским углом при вершине правильной пирамиды и углом при ребре основания
tg
cos x
cos x tg
2
3
2
cos x 3tg
cos x
2
tg
tg
2
n
Зависимость между плоским углом при вершине правильной пирамиды и углом при боковом ребре
x
sin
2
1
2 cos
x
sin
2
1
2 cos
2
2
x
sin
2
3
2 cos
sin
2
x
2
cos
cos
n
2
Зависимость между углом при боковом ребре и плоскостью основания правильной пирамиды
sin x
1
3
ctg
2
sin x ctg
sin x 3ctg
2
2
sin x ctg
2
ctg
Зависимость между углом при ребре основания и углом между боковым ребром и плоскостью основания
1
tgx tg
2
tgx
1
2
tg
tgx
3tg
2
tgx tg cos
n
n
10.
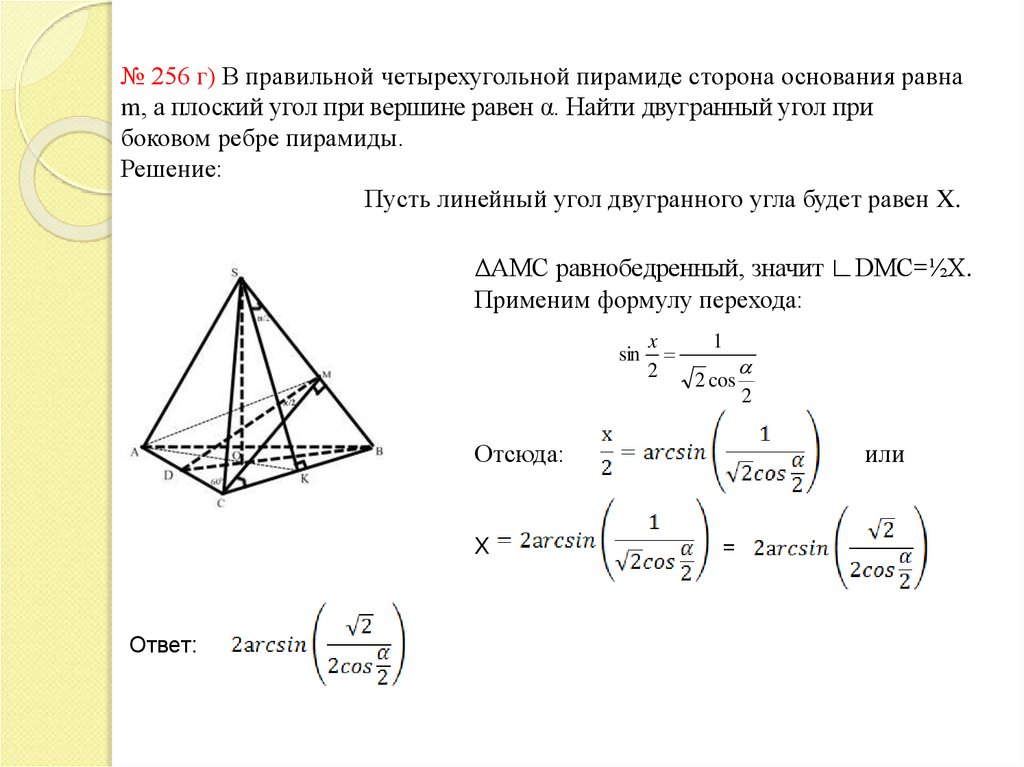
№ 256 г) В правильной четырехугольной пирамиде сторона основания равнаm, а плоский угол при вершине равен α. Найти двугранный угол при
боковом ребре пирамиды.
Решение:
Пусть линейный угол двугранного угла будет равен X.
ΔАМС равнобедренный, значит ∟DMC=½X.
Применим формулу перехода:
sin
x
1
2
2 cos
2
Отсюда:
Х
Ответ:
или
=
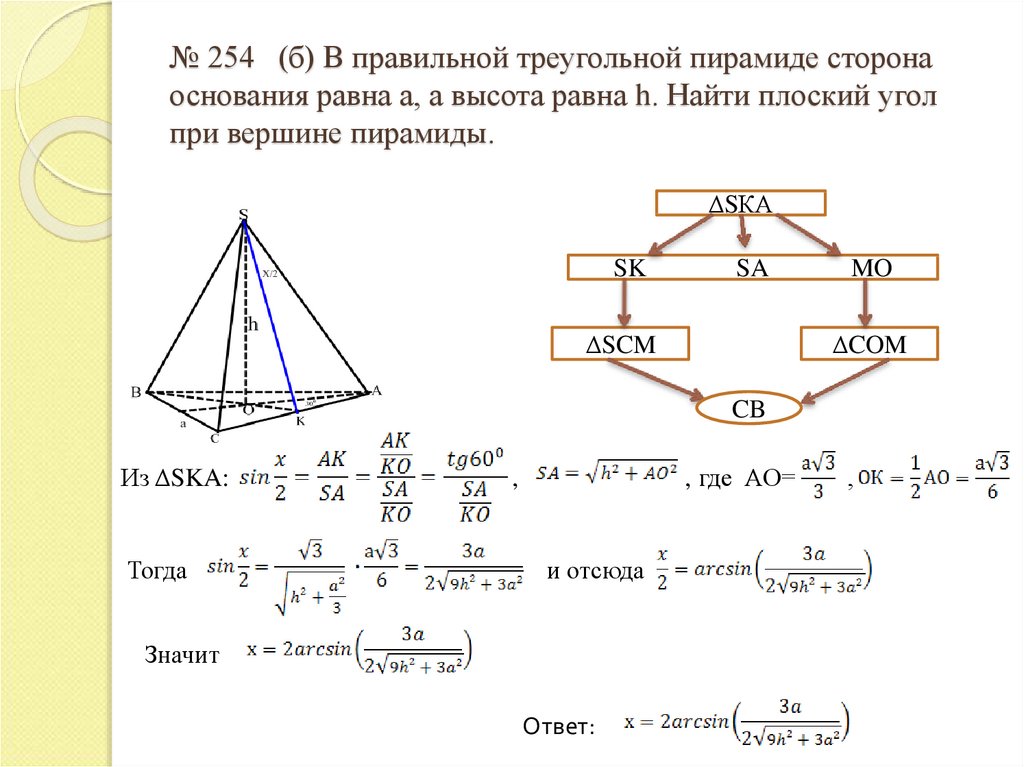
11. № 254 (б) В правильной треугольной пирамиде сторона основания равна а, а высота равна h. Найти плоский угол при вершине
пирамиды.ΔSКА
SK
SA
ΔSCM
MO
ΔCOM
CB
Из ΔSKA:
Тогда
, где АО=
,
и отсюда
Значит
Ответ:
,



 Математика
Математика








