Фильтр Винера

1. Тема: Фильтр Винера.

Кафедра Радиоэлектроники.
Преподаватель:
Лазаренко
Сергей Валерьевич.
Радиотехнические цепи и сигналы. Лекция 16.

2.

Учебные вопросы:
1. Постановка задачи фильтрации.
2. Интегральное уравнение
оптимального фильтра.
3. Коэффициент передачи
оптимального фильтра.
Радиотехнические цепи и сигналы. Лекция 16.

3.

1. Постановка задачи фильтрации.
Например, пусть на вход приемника поступает смесь амплитудномодулированного сигнала
s(t ) U t cos t
и помехи n(t), т.е.
x t s(t ) n(t ) U t cos t n(t )
На вход некоторой системы (фильтра) поступает аддитивная смесь x(t)
полезного сигнала s(t) и шума (помехи) n(t)
x t s(t ) n(t )
Желаемым выходом фильтра является, естественно, сигнал
y0 t s(t )
Реакцией реального фильтра является оценка сигнала, т.е.
y t s * (t )
Требуется найти характеристики реального фильтра, выходное колебание
которого y(t)=s*(t) отличалось бы от желаемого выхода y0(t)=s(t) с минимальной
среднеквадратической погрешностью
M 2 t M s(t ) s * (t )
min
2
(1)
Радиотехнические цепи и сигналы. Лекция 16.

4.

Так как рассматриваемые процессы эргодические, то усреднение
сводится к интегрированию (низкочастотной фильтрации).
Задача может ставиться несколько иначе: по известным
значениям x(t) в прошлом и настоящем дать оптимальную
оценку s*(t+∆), т.е. в будущем.
Радиотехнические цепи и сигналы. Лекция 16.

5.

2. Интегральное уравнение оптимального
фильтра.
Более подробно рассмотрим выражение (1). При этом учтем, что выходной
сигнал искомого реального фильтра определится интегралом Дюамеля
s* t g x t d g s t n t d
0
(2)
0
Где g(τ)- импульсная характеристика искомого реального фильтра.
Для нахождения этой характеристики определим квадрат ошибки
2 t s t s* t 2 s 2 t 2s t s* t s*2 t
s 2 t 2s t g x t d
g g x t x t d d
0
0 0
Усредняя левую и правую части выражения (3), получим
M t M s t 2 g M x t s t d
2
2
0
g g M x t x t d d
(4)
0 0
Радиотехнические цепи и сигналы. Лекция 16.
(3)

6.

Учтем, что M s 2 t s2 - энергия (дисперсия) сигнала s(t),
M x t s t Bxs - взаимная корреляционная функция сигнала s(t) и
принятого сигнала (принятой реализации) x(t),
M x t x t Bx - автокорреляционная функция принятого сигнала.
С учетом этого выражение (4) перепишется в виде
M 2 t 2 s2 2 g Bxs d
0
g g B d d
x
(5)
0 0
Пусть импульсная характеристика какого-то условного фильтра равна
g t g 0 t h t (6)
Где h(t) - произвольная функция, не равная тождественно нулю;
Найдем среднеквадратическую ошибку фильтрации этого условного фильтра,
для чего подставим в выражение (5) соотношение (6).
M 12 t s2 2 g 0 h Bxs d
0
g0 h g 0 h Bx d d
0 0
Радиотехнические цепи и сигналы. Лекция 16.
(7)

7.

Очевидно, что при 0 ошибка фильтрации M 12 t M 2 t минимальна, так
как в этом случае g(t)=g0(t).
Перепишем формулу (7) в следующем виде
M 12 t s2 2 g 0 Bxs d 2 h Bxs d
0
g 0 g 0 Bx d d 2
0 0
0
g h B d d
0
x
0 0
2 h h Bx d d
(8)
0 0
Согласно выражению (5)
M 2 t s2 2 g0 Bxs d
0
Введем обозначения
g g B d d
0
0
x
0 0
Q h Bxs d g 0 h Bx d d
0
(10)
0 0
L h h Bx d d
(11)
0 0
Радиотехнические цепи и сигналы. Лекция 16.
(9)

8.

Подставляя соотношения (9), (10), (11) в выражение (8), получим
M 12 t M 2 t 2 Q 2 L
(12)
Условие минимума
dM 12 t
2Q 2 L 0
d
Q
откуда следует
(13)
L
С другой стороны, как было отмечено ранее, для обеспечения минимума M 12 t
необходимо, чтобы 0. Из выражения (13) следует, что Q=0.
Преобразуем выражение (10) следующим образом, поменяв порядок
интегрирования и приравняв Q=0
Q h Bxs d g 0 Bx d
0
0
d 0
Так как функция h(t) - произвольная функция, не равная нулю, то, следовательно,
нулю равно выражение в квадратных скобках, откуда следует:
Bxs d g 0 Bx d
(14)
0
Радиотехнические цепи и сигналы. Лекция 16.

9.

3. Коэффициент передачи оптимального
фильтра.
Применяя к обеим частям выражения (14) преобразование Фурье и используя
свойства спектра свертки двух функций, получим
S xs K0 S x
(15)
Где Sxs(ɷ) - взаимный энергетический спектр сигнала s(t) и принятой
реализации x(t) (смеси сигнала и шума);
K0(ɷ) - коэффициент передачи мощности оптимального фильтра;
Kx(ɷ) - энергетический спектр принятой реализации x(t) (смеси сигнала и
шума).
Из выражения (15) следует
K 0
S xs
S x
(16)
Если сигнал s(t) и помеха n(t) не коррелированны между собой (что практически
всегда выполняется), то S S
xs
s
S x S s Sn
Радиотехнические цепи и сигналы. Лекция 16.

10.

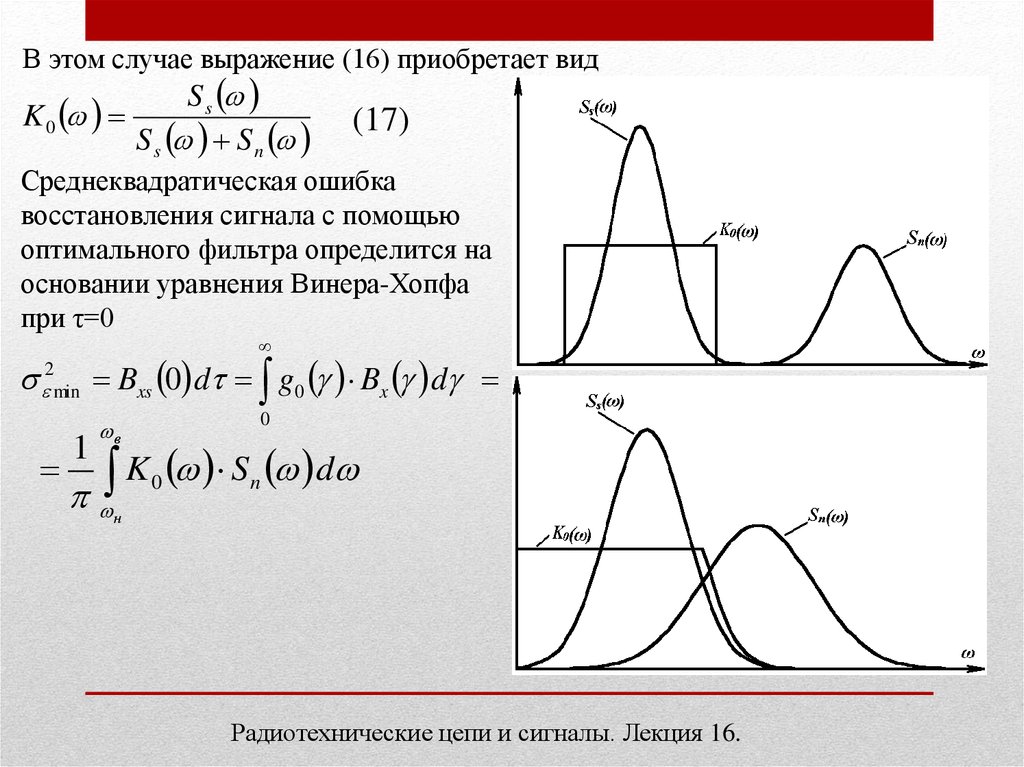
В этом случае выражение (16) приобретает вид
S s
K 0
S s S n
(17)
Среднеквадратическая ошибка
восстановления сигнала с помощью
оптимального фильтра определится на
основании уравнения Винера-Хопфа
при τ=0
2
min
Bxs 0 d g 0 Bx d
0
в
K S d
1
0
n
н
Радиотехнические цепи и сигналы. Лекция 16.