Принцип ортогонального сжатия

1. Принцип ортогонального сжатия

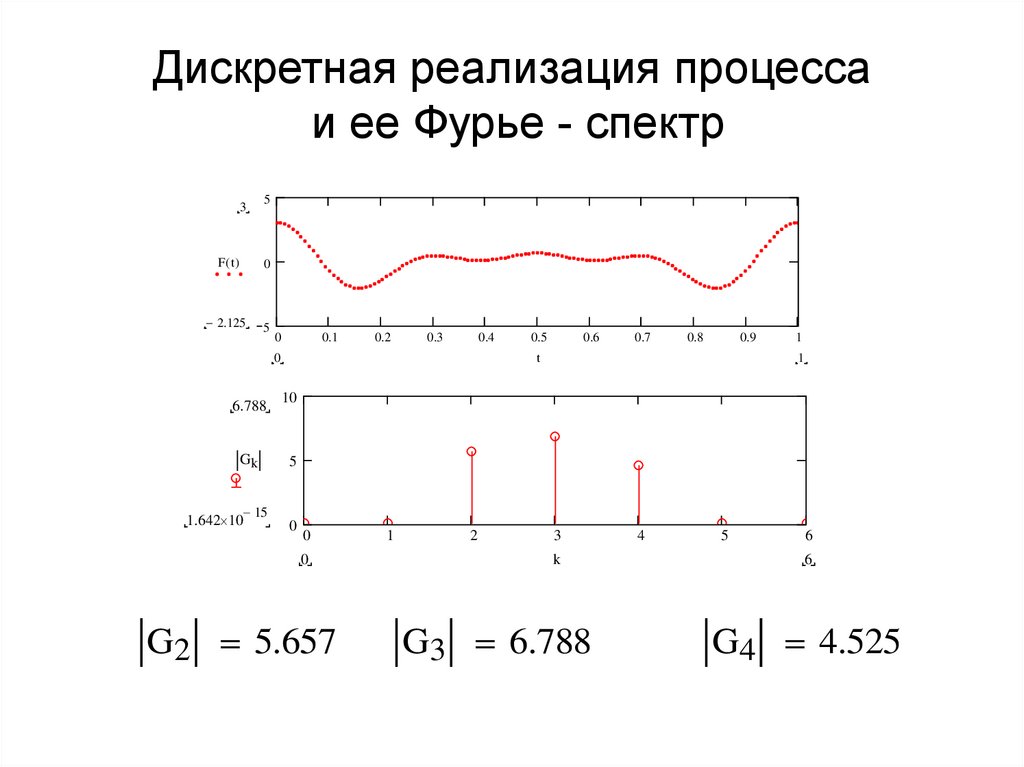
2. Дискретная реализация процесса и ее Фурье - спектр

3
5
F( t )
0
2.125
5
0
0.1
0.2
0.3
0.4
0
6.788
Gk
0.5
0.6
0.7
0.8
0.9
t
1
1
10
5
15
1.642 10
0
0
0
G2 5.657
1
2
3
k
G3 6.788
4
5
6
6
G4 4.525

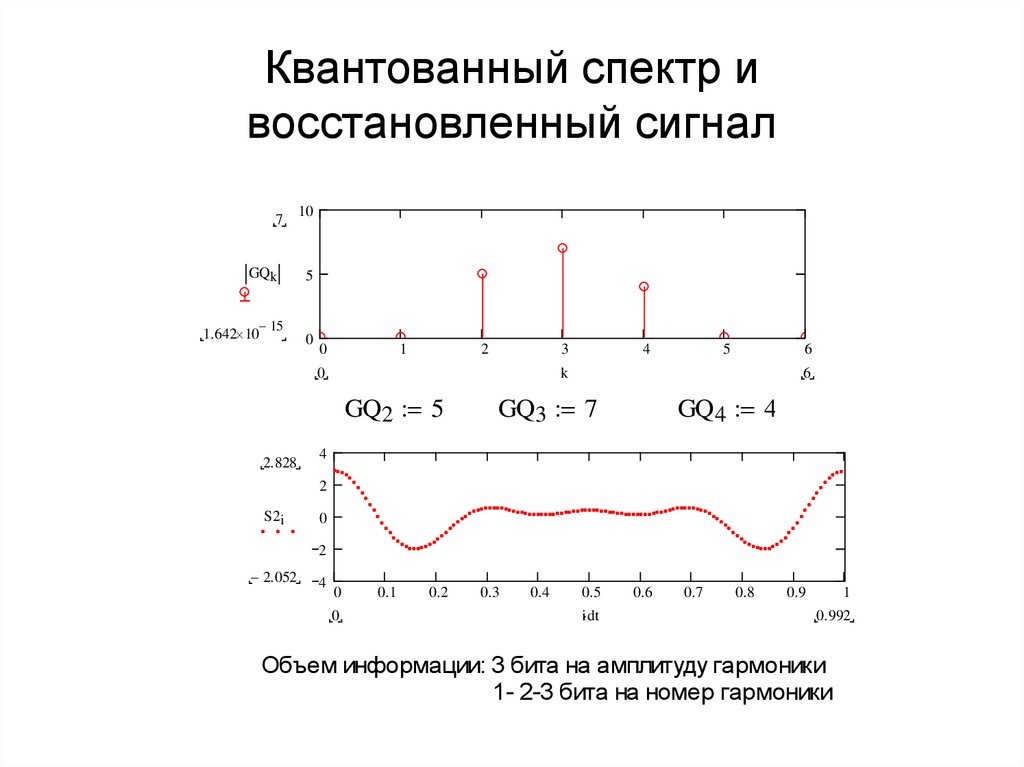
3. Квантованный спектр и восстановленный сигнал

7
GQk
10
5
15
1.642 10
0
0
1
2
3
0
5
6
k
GQ2 5
2.828
4
6
GQ3 7
GQ4 4
4
2
S2i
0
2
2.052
4
0
0
0.1
0.2
0.3
0.4
0.5
idt
0.6
0.7
0.8
0.9
1
0.992
Объем информации: 3 бита на амплитуду гармоники
1- 2-3 бита на номер гармоники

4. Векторное представление сигналов

• Пусть задан сигнал s(t), t [0,T] с энергией ES< .
• Векторным представлением сигнала в с базисом{ k}
называется соотношение
N
s(t) a k k (t)
k 1
a k s, k s(t) k (t)dt
T
• Системы { k}, { k} называются биортогональными, если
1, k m
k (x) m (x)dx k , m k,m 0, k m
• Система называется ортонормальной, если k (x) k (x)
k (x) m (x)dx k , m k,m

5. Классы базисных функций с непрерывным временем

• Гармонические k (x) 1/ 2 exp( j kx)
• Ортогональные полиномы
•Лагерра
•Чебышева, Лежандра
•Эрмита
sin t k
k (t)
t k
• Функции отсчетов
• Уолша Walk(x)
• Функции Хаара hark(x)

6. Дискретные преобразования

Общие соотношения для дискретных преобразований
Рассмотрим общность и различие непрерывного и дискретного преобразований
Непрерывный сигнал
t 0,T
s(t)
k (t)
k , m k (t) *k (t)dt km
T
Ck s(t) *k (t)dt
T
s(t)
Ck k (t)
k 0
Дискретный сигнал
t t n n T , n 0..N 1
s(n) s(t n )
k k (0) k (1) k (2) .. k (N 1)
( k , m )
Ck
N 1
k (n) *m (n) km
n 0
N 1
s(n) *k (n)
n 0
s(n)
Ck k (n)
k 0

7. Дискретные базисные функции

2
W exp j
N
kn
k (n) exp j2 W kn
N
• ДПФ
1 N 1
Ck
s(n)W kn
N n 0
n 0..N 1, k 0..N 1
N 1
s(n) Ck W kn
k 0
• Дискретное косинусное преобразование
k ( n )
• Ck
2
n 0.5
g k cos k
,
N
N
N 1
2
n 0.5
g k s( n )cos k
N
N
n 0
0.5 , k 0
gk
, k 0
1
s( n )
2 N 1
n 0.5
g k Ck cos k
N k 0
N

8. Двумерное ДКП- DCT преобразование

Прямое и обратное ДКП (DCT- IDCT) преобразование
C S T ,
S TC .
S= s( i , j ) - исходный блок, i, j = [0, N-1]
С= Ckm - его спектр
k, m =[0, N-1]
Матрица преобразования DCT
0.5
k 0
2
k (i) NN
,
k 0
N cos( k (i 0.5)
N
k=0..N-1, i=0..N-1

9.

Исходное изображение «Masha»

10.

Исходный блок «Глаз»
183
168
148
131
108
23
S *
2
35
11
44
92
116
178
158
136
120
94
12
27
98
20
15
69
114
171
150
122
111
84
3
78
120
19
5
50
109
166
144
111
104
71
3
82
129
18
14
86
131
161
134
108
99
52
7
18
22
13
47
101
132
151
123
108
102
59
7
14
21
42
77
116
133
146
118
105
93
49
3
21
58
73
75
105
132
142
119
103
90
43
3
12
41
63
68
96
102
131
113
101
95
51
8
9
16
39
60
71
105
126
112
96
95
57
15
10
14
61
106
134
185
125
108
90
92
60
22
21
17
149
159
178
199
113
101
89
96
67
30
57
19
66
150
168
197

11.

Ортогональное преобразование
C S
788
70
303
62
C
44
0
14
30
T
0.5
2
(n 0.5)
N cos( m
N
17
9 21 18 15
13
2 27 22 5
11 13 22 12 17
6
4
0
11
22
26 19 16
22 4
27 15 19 22 14
13 14
34
0 16 1
5 10 1
47 19 26 10 16 15 9
20
182
25
26
51
57
31
5
15
9

12.

Квантование
Round (
*
i, j
C
Ci , j
Qi , j
)
788
23
60
8
2
C
4
0
1
2
6
36
3
2
4
11
4
0
1
0
2
1
1
0
1
1
0
1
0
1
1
2
1
0
0
1
1
0
0
1
2
2
2
1
0
1
1
0
1
1
0
0
0
0
0
0
0
0
788
3
7
1
0
0
0
0
0
4
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
C 20
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0

13.

Деквантование
Ci , j Ci*, j Qi , j
788
69
300
56
2
C
36
0
13
30
C 20
14
9 11 13 15
9
0 26 15 0
11 13 15 0
0
0
0
0
0
21
15 17 0
21
0
26 15 17 19 0
0
0
30
0
0
0
0
0
0
34 19 21 0
0
0
0
18
180
21
18
44
788 0
63 164
287 0
61
0
0
0
0
0
0
0
0
0
55
28
0
11
0
41
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

14.

Результат восстановления
RLE: 14953 байт (сжатие: 25,29)
RLE+Huffman: 11047 байт (сжатие: 34,24)
RLE+Arithm: 11022 байт (сжатие: 34,32)
PSNR(Y)=20,578 дБ, сжатие: 34,32