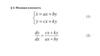Ортогональные функции

1. Ортогональные функции Ортогоналды функциялар

φ(t) , ψ(t)
[a,b]
b
(t ) (t )dt
a
0

2. Ортогональная система функций Ортогоналды функциялар жүйесі

b
(
t
)
(
t
)
dt
0
,
n
m
a
n m;
b
n, m 0,1,...
2
[
(
t
)
]
n dt n 0
a

3. Ортогональная система функций Ортогоналды функциялар жүйесі

n 1
Нормальная система
n (t )
{
}
n

4. Ортогональная система функций Ортогоналды функциялар жүйесі

{1, cos(t), sin(t), cos(2t), sin(2t),…,cos(nt), sin(nt),…} –
система ортогональна на промежутке длиной 2π
1 cos(t ) sin( t ) cos( 2t ) sin( 2t )
{
,
,
,
,
,...}
2
- на промежутке длиной 2π нормальная система
На [0, π] не будет ортогональной

5. Ортогональная система функций Ортогоналды функциялар жүйесі

Проверить на ортогональность:
2
cos(t )dt ,
0
2
cos(t ) sin( t )dt
0
2
cos(t ) cos(t )dt
0
cos(t )dt,
0
cos(t ) sin( t )dt 0,
0
cos(t ) cos(t )dt
0

6. Ортогональная система функций Ортогоналды функциялар жүйесі

Полиномы Лежандра
1
dn 2
Pn (t ) n
n (t 1) n
2 n! dx
, n=0,1,2,…
на интервале [-1,1].
3
1
5
3
P0 (t ) 1; P 1(t ) t ; P 2 (t ) t 2 ; P3 (t ) t 2 t ,
2
2
2
2

7. Ортогональная система функций Ортогоналды функциялар жүйесі

1
2
1[ Pn (t )] dt 2n 1
2
1
n
2

8. Ортогональная система функций Ортогоналды функциялар жүйесі

Полиномы Лагерра
1 t d n n t
Ln (t ) e
(t e )
n
n! dt
на интервале [-1,1].
1
L0 (t ) 1; L1 (t ) t 1; L2 (t ) t 2 2t 1
2

9. Ортогональная система функций Ортогоналды функциялар жүйесі

Полиномы Лагерра
2
ïðè m n
1 Pm (t ) Pn (t )dt 2n 1
0
ïðè m n
1

10. Ортогональная система функций Ортогоналды функциялар жүйесі

Полиномы Чебышева
Tn (t )
2
cos( n arccos t ), n 1.
на интервале [-1,1].
1
2
8 2 1
32 3 3
T0 (t )
; T1 (t )
; T2 (t )
(t ); T3 (t )
(t t ).
x
2
4

11. Периодические функции

f (t )
A
k 1
k
cos( k t k )
2
T
f (t ) Ak cos( k t k )
k 1

12. Периодические функции

1
1
sin t sin 2t sin 3t
2
4
1,20
1,00
0,80
0,60
Ряд1
0,40
0,20
0,00
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19

13. Ряд Фурье

a0
f (t )
a k cos( kt bk sin kt)
2 k 1
-ряд Фурье

14.

Определение коэффициентов ряда Фурье
a0
S { f (t ) [ ak cos( kt) bk sin( kt)]}2 min
2 k 1

15. Обозначим скалярное произведение функций

T
( т , m ) n (t ) m (t )dt ;
0
T
( т , f ) n (t ) f (t )dt
0

16. Система для определения коэффициентов ряда Фурье

a0 ( 0 , 0 ) + a1 ( 0 , 1 ) + … + aN ( 0 , N ) = ( 0 , f);
…………………………………………………
a ( , ) + a ( , ) + … + a ( , ) = ( , f).
1
1
N
N
N
N
N
0 0 N

17. Ряд Фурье

a0
f (t ) ak cos( kt) bk sin( kt)
2 k 1
a0
ak
bk
1
1
1
f (t )dt
f (t ) cos ktdt, k 1,2,3,...
f (t ) sin ktdt, k 1,2,3,...

18. Ряд Фурье

f(t) – четная
на
a0
2
f (t )dt
0
f(t) – нечетная на
bk
2
[ , ], bk 0
2
ak f (t ) cos ktdt, k 1,2,3,...
0
[ , , ], ak a0 0
f (t ) sin ktdt, k 1,2,3,...
0

19. Ряд Фурье

Пример 1
a, 0 t
f (t )
a, t 2
a0 0,
ak 0, k 1, ,2,3.....

20. Ряд Фурье

Пример 1
bk
2
f (t ) sin ktdt
0
2
a sin ktdt
0
2a
[ cos kt]
k
0
2a
[ cos k 1]
k
0, k chet
2a
[1 ( 1) k ] 4a
k
, k nechet
k
4a
1,
1
f (t )
[sin t sin 3t sin 5t ...]
3
5
A1
4a
A2 0
4a
A3
3
....
1
k
2

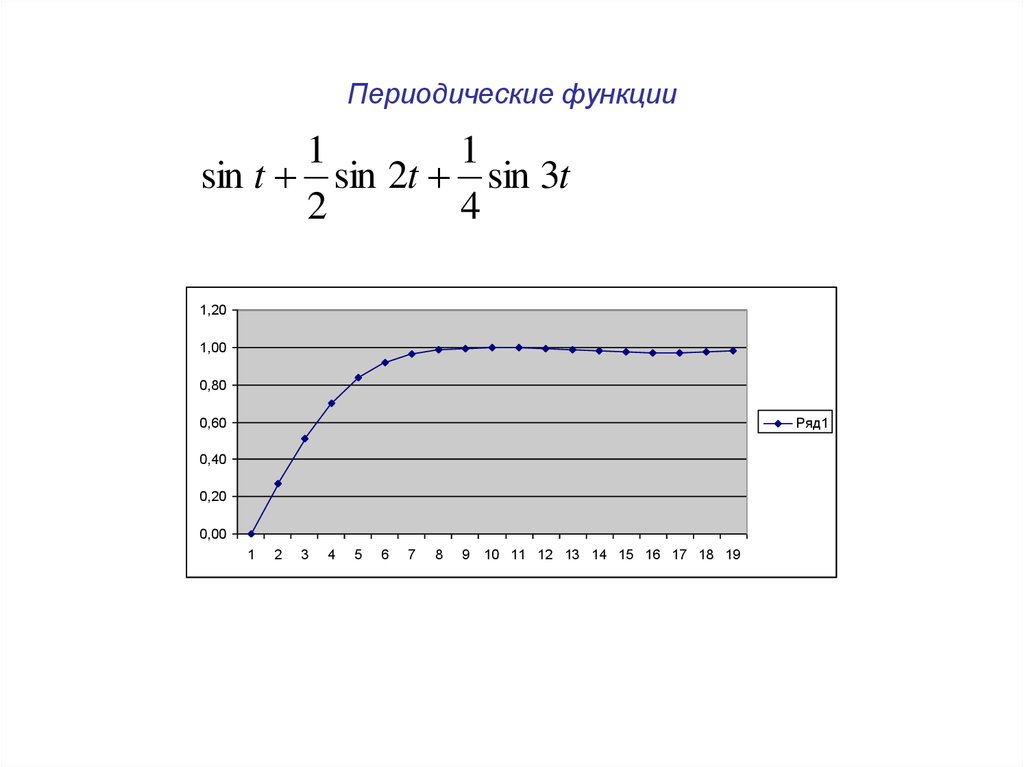
21. Ряд Фурье

Пример 1
1,4
1,2
1
0,8
Ряд1
0,6
0,4
,
0,2
0
-0,2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
-0,4
-0,6
Ряд2
Ряд3

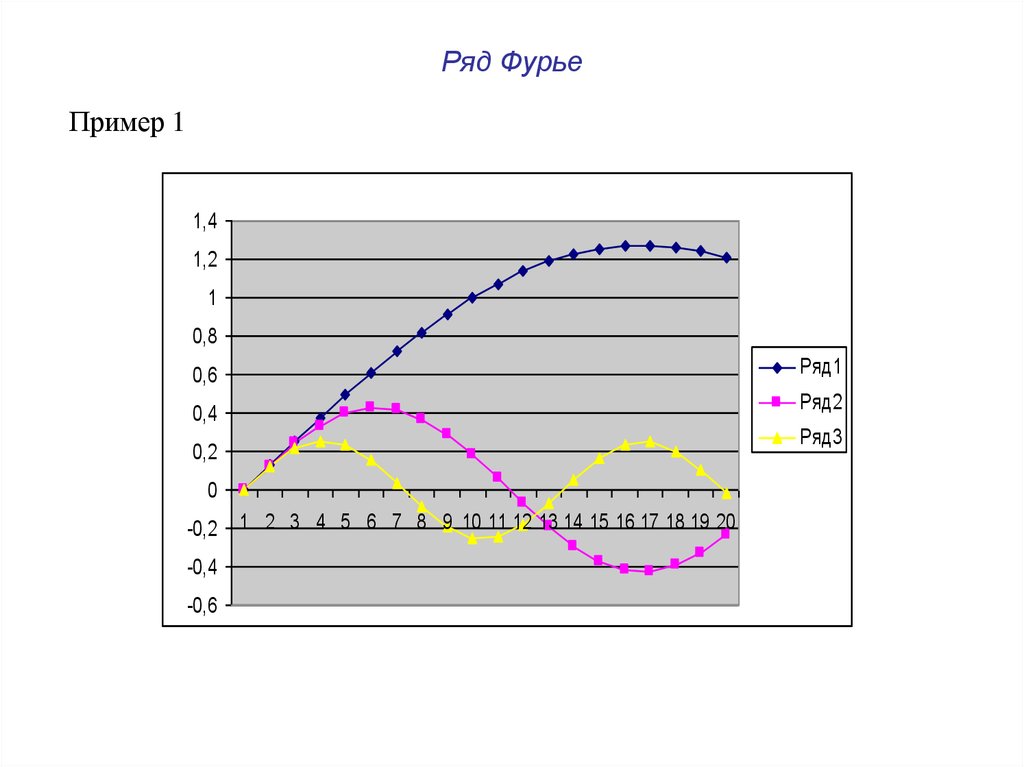
22. Ряд Фурье Непериодические функции

Пример 2
f (t ) t
[ , ]
,

23. Ряд Фурье Непериодические функции

Пример 2
a0
2
tdt
0
0, k chet
2
k
a k t cos ktdt ... 2 [( 1) 1] 4
0
, k nechet
k
k 2
2
,
4 cos t cos 3t cos 5t
f (t ) ( 2 2 2 ...)
2 1
3
5

24. Ряд Фурье Непериодические функции

4 cos t cos 3t cos 5t
f (t ) ( 2 2 2 ...)
2 1
3
5
3,5
3
,
2,5
2
Ряд1
1,5
Ряд2
1
Ряд3
0,5
Ряд4
0
Ряд5
-0,5
-1
-1,5
1
2
3
4
5
6
7