Похожие презентации:
Линейная алгебра
1. Линейная алгебра
Определители второго порядкаСистемы из двух линейных уравнений с двумя
неизвестными
Определители n – ого порядка
Методы вычисления определителей
Системы из n линейных уравнений с n
неизвестными.
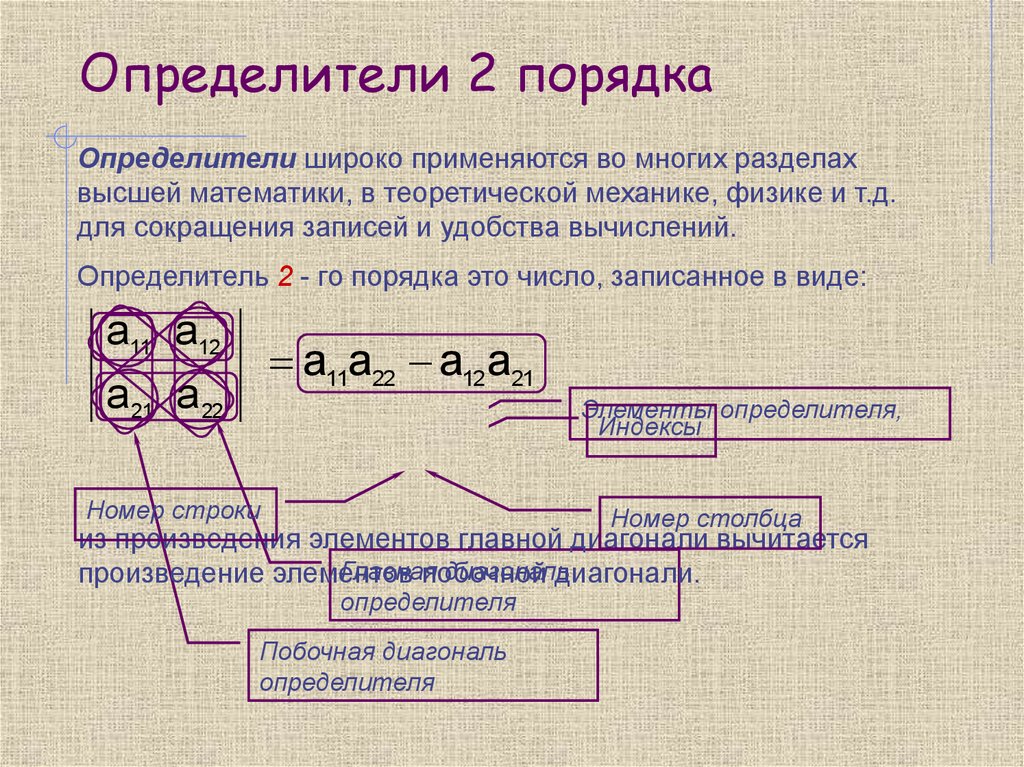
2. Определители 2 порядка
Определители широко применяются во многих разделахвысшей математики, в теоретической механике, физике и т.д.
для сокращения записей и удобства вычислений.
Определитель 2 - го порядка это число, записанное в виде:
a11 a12
a11a22 a12a21
a 21 a 22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя
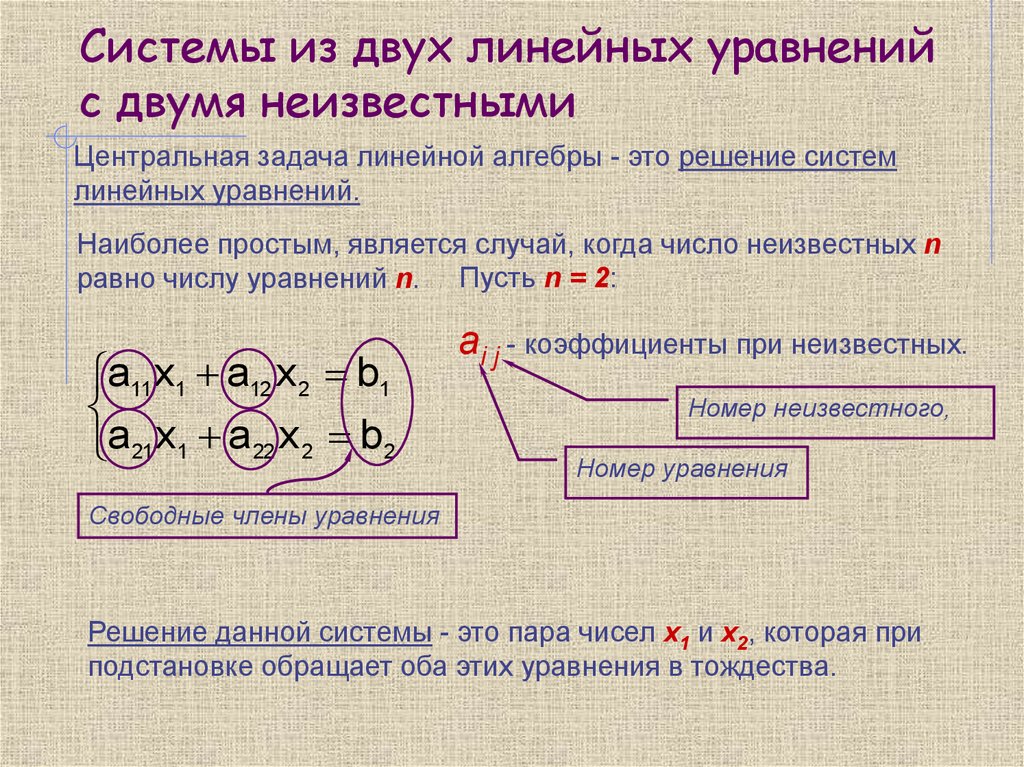
3. Системы из двух линейных уравнений с двумя неизвестными
Центральная задача линейной алгебры - это решение системлинейных уравнений.
Наиболее простым, является случай, когда число неизвестных n
равно числу уравнений n. Пусть n = 2:
a11x1 a12 x 2 b1
a21x1 a22 x 2 b2
ai j - коэффициенты при неизвестных.
Номер неизвестного,
Номер уравнения
Свободные члены уравнения
Решение данной системы - это пара чисел х1 и х2, которая при
подстановке обращает оба этих уравнения в тождества.
4. Системы из двух линейных уравнений с двумя неизвестными
a11x1 a12 x 2 b1a21x1 a22 x 2 b2
a11 a22 x1 a12 a22 x 2 b1 a22
a12 a21 x1 a12 a22 x 2 a12 b2
a
11
a22 a12 a21 x1 a22 b1 a12 b2
Обозначим:
1
b1 a12
b2 a22
a11 a12
a 21 a 22
a11 a22 a12 a21
b1 a22 a12 b2
x1 1
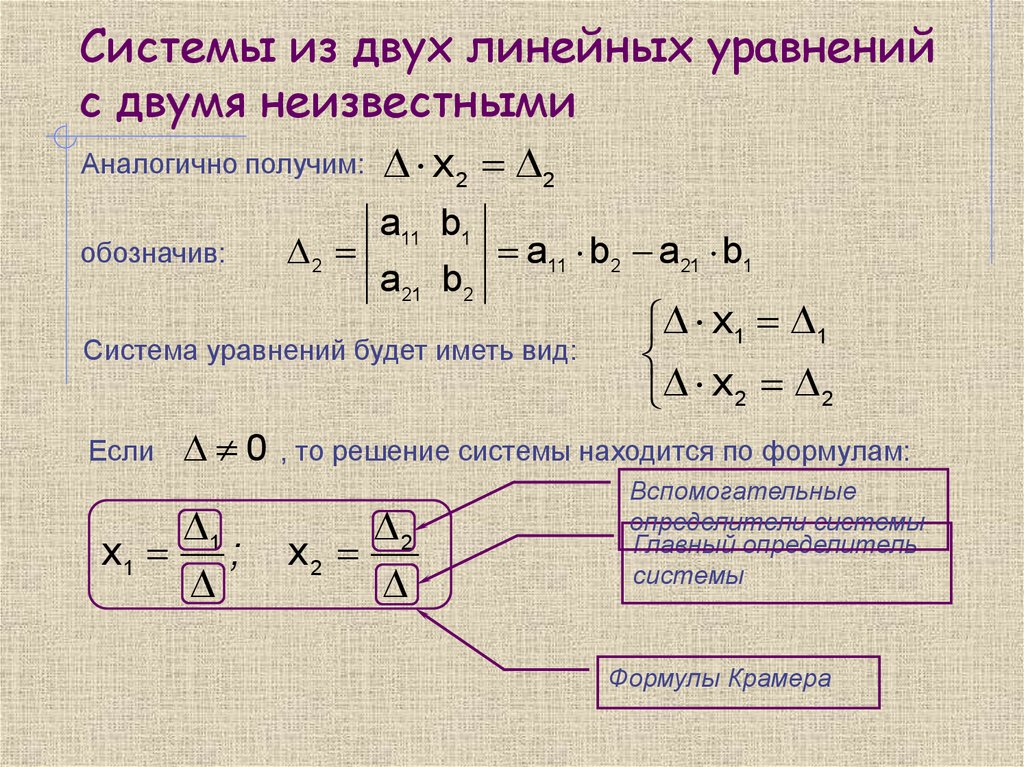
5. Системы из двух линейных уравнений с двумя неизвестными
Аналогично получим:обозначив:
2
x 2 2
a11 b1
a21 b2
a11 b2 a21 b1
Система уравнений будет иметь вид:
Если
0
1
x1
;
x1 1
x 2 2
, то решение системы находится по формулам:
2
x2
Вспомогательные
определители системы
Главный определитель
системы
Формулы Крамера
6. Системы из двух линейных уравнений с двумя неизвестными
Решить систему методом Крамера:2x1 x 2 5
3x1 2x 2 3
Вычислим главный и вспомогательные определители системы:
21
2 2 3 1 1
3 2
5 1
1
5 2 3 1 7
3 2
2 5
2
2 3 3 5 9
3 3
Найдем решение системы по формулам Крамера:
7
x 1 7;
1
9
x2
9
1
7. Определители n – ого порядка
Определителем n – ого порядка называется число:a11 a12 a1n
a21 a22 a 2n
an1 an2 ann
Методы вычисления определителей n – ого порядка рассмотрим
на примере вычисления определителей третьего порядка.
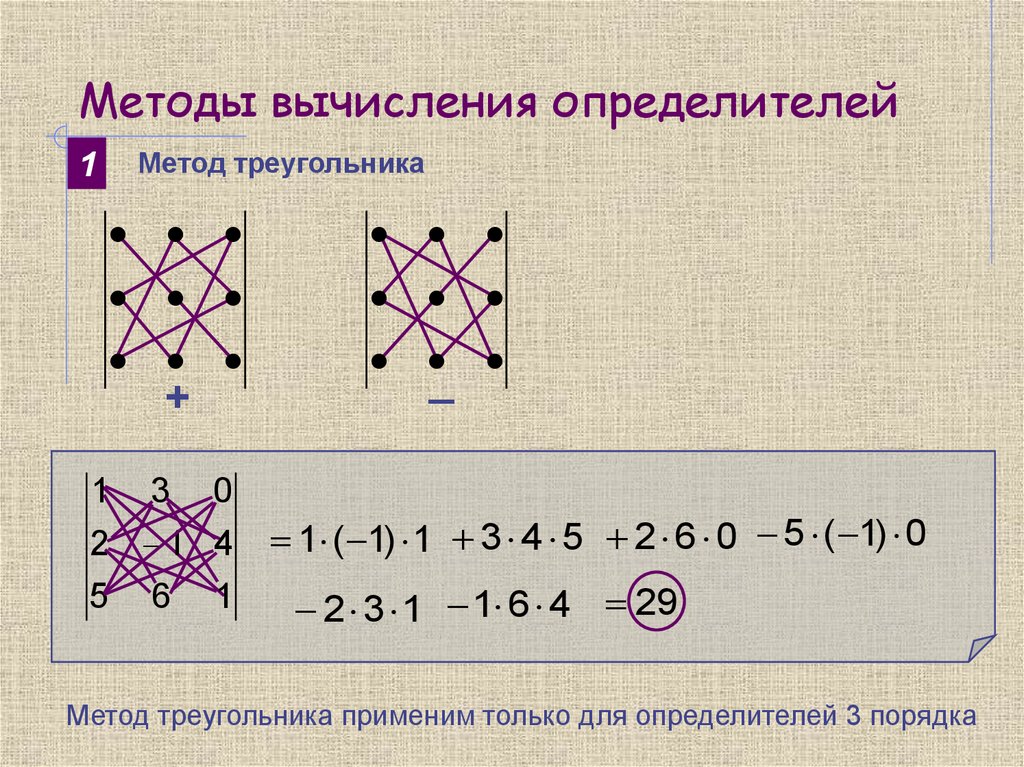
8. Методы вычисления определителей
1Метод треугольника
+
1 3 0
2 1 4
5 6 1
_
1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
2 3 1 1 6 4 29
Метод треугольника применим только для определителей 3 порядка
9. Методы вычисления определителей
2Метод разложения определителя по элементам строки
(столбца)
Определитель второго порядка, который получается из определителя
3 - го порядка путем вычеркивания i - й строки и j - го столбца, т.е.
строки и столбца, на пересечении которых стоит элемент
называется минором элемента и обозначается
Алгебраическим дополнением элемента
Ai j Mi j ( 1)i j
aa1111
aa2121
aa3131
aa1212 aa1313
aa2222 aa2323
aa3232 aa3333
ai j
ai j
Mi j
называется
aa2211 aa2312
MM1123
aa3231 aa3332
1 1 2 3
A
M
(
M23
A11 23 M11 23( 1) 1) M
11
10. Методы вычисления определителей
Величина определителя равна сумме произведений элементовкакой – либо строки (столбца) определителя на их
алгебраические дополнения:
n
ai j A i j
Разложение определителя по элементам
i – ой строки
ai j A i j
Разложение определителя по элементам
j – ого столбца
j 1
n
i 1
2 1 0
0 1
0 3
3 1
1 2
1 1
0 3 1 2
( 1) 0
( 1)1 3
( 1) 1
2 1
2 5
5 1
2 5 1
2 (3 1 5 1) 1 (0 1 2 1) 2
11. Методы вычисления определителей
3Использование свойств определителя
Свойства определителя:
Величина определителя:
равна нулю, если элементы какого - либо столбца или строки
равны нулю:
0 0
a21 a22
0 a22 0 a21 0
равна нулю, если соответствующие элементы двух строк
(столбцов) равны
a11 a12
a11 a12
a11 a12 a11 a12 0
12. Методы вычисления определителей
меняет знак, если поменять местами строки (столбцы):a11 a12
a21 a22
a11 a22 a12 a21 a12 a21 a11a22
a12 a11
a22 a21
увеличивается в k раз, если элементы какого - либо столбца
(строки) увеличить в k раз:
k a11 k a12
a21
a22
k a11 a22 k a12 a21 k
a11 a12
a21 a22
не меняется при замене строк соответствующими столбцами:
a11 a12
a21 a22
a11 a21
a12 a22
13. Методы вычисления определителей
не меняется, если к элементам какой-либо строки (столбца)прибавить соответствующие элементы другой строки (столбца),
умноженные на произвольный множитель
a11
a12
a 21 ka11 a 22 ka12
a11a 22 a 21a12
a11a 22 a11ka12 a 21a12 ka11a12
a11 a12
a 21 a 22
Если определитель имеет так называемый треугольный вид,
то он вычисляется как произведение чисел, стоящих на
главной диагонали: a a a
11
12
13
0 a22 a23 a11a22 a33
0 0 a33
14. Методы вычисления определителей
1 3 11
3 1 1 3 1
5 1
2 1 3 0 5 1 0 5 1 1
( 1)1 1
7 2
1 4 1
1 4 1 0 7 2
5 2 7 1 17
Выберем 1
К элементам
2
Разложим
столбец
и
К элементам
3
строки
прибавим
определитель
по
превратим
второй
строки
прибавим
элементы 11строки,
элементам
столбца
и третий
элементы
1
строки
умноженные на (-2)
элементы в нули
Также, используя свойства, можно привести определитель к
треугольному виду и вычислить по последнему свойству.
15. Системы из n линейных уравнений с n неизвестными
Рассмотрим общую квадратную систему линейных уравнений:a11x1 a12 x 2 a1n x n b1
a21x1 a22 x 2 a2n x n b2
an1x1 an2 x 2 ann x n bn
Система линейных уравнений называется совместной, если она
имеет решение и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет
единственное решение и неопределенной, если она имеет
бесконечное множество решений.
Система называется однородной, если b1 b2 bn 0
Однородная система совместна, так как всегда имеет нулевое
решение.
16. Системы из n линейных уравнений с n неизвестными
Для сокращения выкладок запишем систему из трех уравнений стремя неизвестными:
a11x1 a12 x 2 a13 x 3 b1
a21x1 a22 x 2 a23 x 3 b2
a x a x a x b
33 3
3
31 1 32 2
a11 a12 a13
a 21 a 22 a 23
a31 a32 a33
Вспомогательные определители получаются из главного
определителя, если заменить соответствующий столбец столбцом
свободных членов:
b1 a12 a13
a11 b1 a13
a11 a12 b1
1 b 2 a 22 a 23
2 a 21 b 2 a 23
3 a 21 a 22 b 2
b3 a32 a33
a31 b3 a33
a31 a32 b3
17. Системы из n линейных уравнений с n неизвестными
По величине главного и вспомогательных определителей можносудить о характере системы:
Если
0 то система совместна и определенна.
Если 0, 1
неопределенна.
2 3 0
Если 0, но 1 0 или
система несовместна.
то система совместна и
2 0
или
3 0
то
В общем случае будем иметь n +1 определителей n – ого порядка
, 1, 2 , 3 , , n 2 , n 1, n
и, если 0 , то решение системы находится по формулам
Крамера:
1
x1 ;
2
x2
;
n
xn













 Математика
Математика








