Похожие презентации:
Метод гомогенизации. (Лекция 11)
1. Введение в асимптотические методы. Лекция 11
Метод гомогенизации2. 1. Что такое гомогенизация?
Гомогенизация – математический методпозволяющий получать уравнения,
описывающие исследуемые процессы на
макроуровне из уравнений на микроуровне
(“upscaling”). Дает
Структуру макроскопических уравнений и
формулы для коэффициентов
Средства математически строгого
доказательства сходимости решений
микроскопических задач к решению
макроскопической задачи.
3. 2. Основная идея
?0.1
0.05
0.2
0
Семейство задач
Исходная задача
k ( x) p 0
вложение
k ( x) p 0
k k ( x / )
Нахождение
предела
p0
Работа метода гомогенизации состоит в отыскании диф. уравнения,
которому удовлетворяет предел
p0 lim p
0
4. 3. Первый пример: 1-D фильтрация.
dd
k ( x)
p 0, 0 x 1
dx
dx
p (0) 1, p (1) 0
1
k k ( x / )
(1)
k ( y ) заданная периодическая
функция с периодом 1
1.5
dp
dx
q
k
(
x
)
Const
q
1 (3)
(2)
k ( x)
dx
0
1
1/
1
dx
dy
dy
O
(4)
k ( x)
k ( y) 0 k ( y)
0
0
1
1 dy
q q0
(5) q kharm
dp0 (8)
k
(
y
)
q
k
0
0
harm
dx
p p0
(6) p p0 ( x) p1 ( x / )
k
=1/20
1
0.5
k
p1 ( y) harm 1 dy
k ( y)
0
y
(7) p0 1 x,
0
0
1
0.9
0.2
0.4
0.6
0.8
1
p
0.8
0.7
0.6
0.5
0.4
0.3
0.2
x
0.1
0
0
0.2
0.4
0.6
0.8
1
5. 4. Первый пример: результаты.
Рассмотренная техника обладает всеми основнымипризнаками метода гомогенизации.
Мы доказали существование пределов для потока и давления
(а именно макроскопических потока и давления) при 0
Мы нашли, что макро-поток и макро-давление связаны между
собой тем же соотношением, что микроскопические
характеристики, но проницаемость (эффективная
проницаемость) является константой на макроуровне
Мы подсчитали эффективную проницаемость (оказавшуюся
равной гармоническому среднему)
Мы определили вид микроскопического давления как сумму
тренда (макроскопического давления) и малого периодически
осциллирующего члена. Эта структура является общей в
методе гомогенизации.
6. 5. Пример: Слоистая среда
k ( x1 , x2 ) k ( x2 / )k ( x) p 0, 0 x1 , x2 1
k ( y)
заданная периодическая функция с периодом 1
Ожидается, что среда может
быть описана в среднем как
k
x2
x2
( x1 , 0)
p
( x1 ,1) 0
x2
p ( x1 , x2 ) x1 ,
p ( x1 , 0) 0, p ( x1 ,1) 1
p=0
p (0, x2 ) 0, p (1, x2 ) 1
(3) p
Задача для k
p=1
Задача для
K p0 0, (1)
k
K
0
x1
q k p k e1
x2
p ( x1 , x2 ) x2 p1 ( x2 / ),
1
1
1
0
0
0
0
p 0
p0
x1
k karith
Q2 k geom
p0
x2
x1
q kharm e2
Q1 q ,1dx2 k ( x2 )dx2 k ( y )dy Q2 q ,2 dx1 kharm
Q1 karith
p 1
(4)
p
p
(0, x2 ) (1, x2 ) 0
x1
x1
1
0
(2)
k
k kharm
7. 6. Пример: Слоистая среда
Почему результаты верны?Мы верно угадали вид макроскопического уравнения
Мы верно угадали вид задач (задачи на ячейке в
теории гомогенизации) которые нужно решить для
вычисления эффективных параметров среды
Но что мы будем делать в случае более сложной
среды или более сложных микроскопических
уравнений?
Мы нуждаемся в математической процедуре
Вывода макроскопических уравнений
Вывода задач на ячейке которые нужно решить для
вычисления эффективных параметров среды
Искомая процедура по существу есть адаптированный
к рассматриваемой задаче метод многих масштабов
8. 7. Асимптотическое разложение: 1ый Шаг
k ( x) k ( x / )k ( x) p f ( x) 0,
периодическая функция с ячейкой
k ( y)
Y {0 yi 1, i 1,
Формальное 2-масштабное асимпт. разложение
(1)
n}
медленная к-та
(2)
p p0 ( x, y ) p1 ( x, y ) p2 ( x, y )
Y -периодична по отношению к y x /
где pi ( x, y) есть
1
- дифф-ие сложной функции (3)
x y
быстрая к-та
2
2 y k ( y ) y p0
(4)
k ( y) p
1 y k ( y ) y p1 y k ( y ) x p0 k ( y ) x y p0
0
1
y
y
2
f 0
y
k ( y ) x p1 k ( y ) x y p1 k ( y ) x x p0
9. 8. Асимптотическое разложение: 2ой Шаг
Члены при(1)
2 дают
y k ( y ) y p0 ( x, y ) 0
+ Y-периодичность
параметр y-задачи
Периодическое решение задачи y k ( y ) y p( y ) 0 есть
1-D :
dp
C
(2)
dy k ( y )
p Const
1
C k 1 ( y ) dy p(1) p(0) C 0
0
dp
0
dy
0 в силу периодичности
>0 в силу положительности k
p Const
p0 p0 ( x)
!!!
10. 9. Асимптотическое разложение: 3ий Шаг
Члены при1
дают
y k ( y ) y p1 y k ( y ) x p0 k ( y ) x y p0 0
k ( y) p0 ( x)
y k ( y) y p1
xi
i 1 yi
n
Задача для
p1 линейна и
p0 ( x)
p1 Ni ( y)
xi
i 1
n
(1)
p0 / x1 не зависят от y
Задачи на ячейке
y k ( y ) y N i
k ( y )
i 1,
yi
n
!!!
11. 10. Асимптотическое разложение: 4ый Шаг
Члены при(1)
0
дают
y k ( y ) y p2 y k ( y ) x p1 k ( y ) x y p1 k ( y ) x x p0 f ( x)
Разрешимость уравнения
k ( y) p dy k ( y) p dy k ( y)
y
y
2
y
Y
(2)
1
Y
Y
Если ( y )
x
y p1 dy
Y
k ( y ) x x p0 dy f ( x)dy
Y
(3)
x
p0 ( x)
Ni ( y )
xi
i 1
n
Y -периодична то y ( y) dy 0
Y
0 0 y1 dy1dy2 0 (1, y2 ) (0, y2 ) dy2 0
n
n
N j
2 p0 ( x)
Макроскопическое
kij
f ( x) 0, kij k ( y) ij
уравнение
xi x j
yi
i 1 j 1
Y
1 1
(4)
1
Д-во:
dy
!!!
12. 11. Асимптотическое разложение: Результат
РеологияБалансовое ур-е
Микроскопическая модель:
q f ,
q k ( x) p
?
Макроскопическая модель:
q0 f ,
q0 K p0 , K {kij }
q ( x, y ) k ( y ) 1 y x p0 ( x) p1 ( x, y )
k ( y ) x p0 y p1 O( ) k ( y ) x p0 y N ( y ) x p0
q0 ( x) q ( x, y) dy O( )
Y
O( )
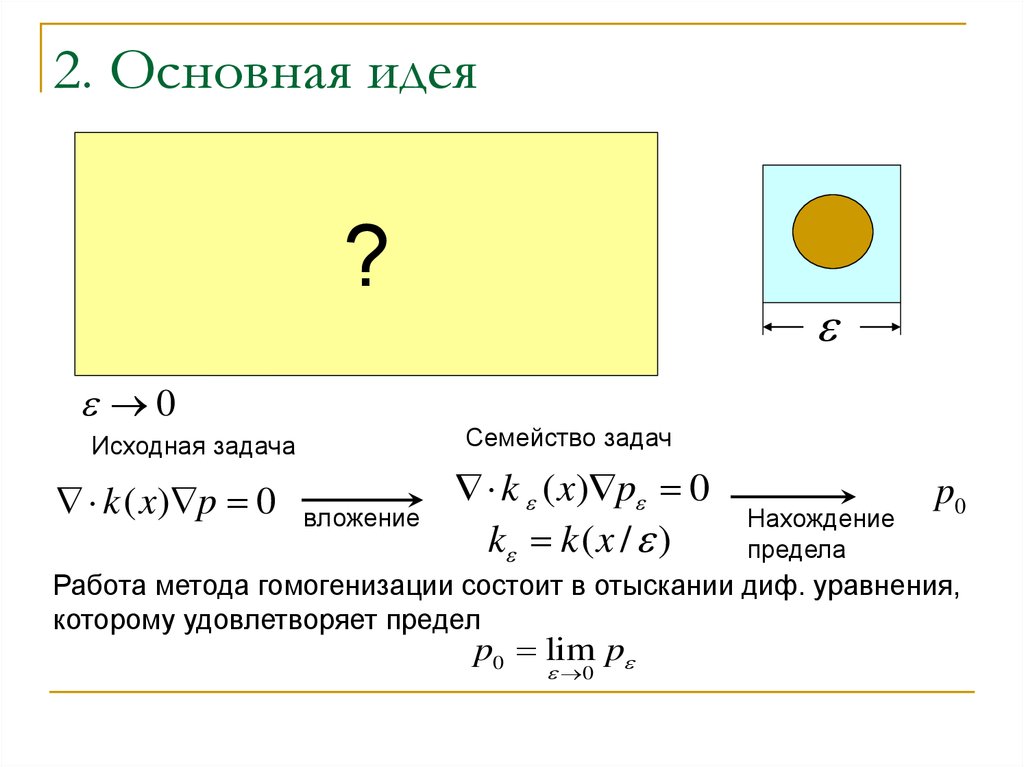
13. 12. Эффективные коэф-ты : общие свойства
Тензор эффективной проницаемости не обязательнодиагонален
(1)
Но не здесь
Диагонален здесь
Тензор K симметричен
=
Задача на ячейке
Ni
k
dy Ni
dy Ni y k ( y ) y N j dy k ( y) y Ni y N j dy
(2) kij karith ij k
y j
y j
Y
Y
Y
Y
n
k 0 0
k k ( y) N e e dy k ( y) N e N e dy
Справедлива оценка k
K k
k
k k
Тензор K положительно определен
ij i
i , j 1
ij
y
i
i
j
Y
y
i
i
y
j
j
Y
2
harm
arith
harm
j
n
i , j 1
ij i
j
arith
2
14. 13 Эффективные к-ты : наша интуиция в порядке.
y2(1)
k ( y1 , y2 ) k ( y1 , y2 )
k ( y1 , y2 ) k ( y1 , y2 )
y1
(2)
1/ 2
1/ 2
N1 ( 1/ 2, y2 ) N1 (1/ 2, y2 )
(6)
N1 ( 1/ 2, y2 ) N1 (1/ 2, y2 )
N1
(8)
N1
y2
y1 1/ 2
N1
y2 1/ 2
N1 ( y1 , y2 ) N1 ( y1 , y2 )
N1 ( y1 , y2 ) N1 ( y1 , y2 )
N1
N1
N1 ( y )
(4)
(
y
,
y
)
(
y
,
y
)
k
k
(
y
)
0
(3)
1
2
1
2
12
y2
y2
y2
Y
(5)
(7)
k ( y )
y1
y1 1/ 2
N1
y2
0
0
y2 1/ 2
M1 y1 N1 ( y)
y k ( y ) y M 1 ( y ) 0
M 1
k11 k ( y )
dy
y1
Y
M1=+1/2
1/ 2
y k ( y ) y N1 ( y )
M1=-1/2
1/ 2












 Математика
Математика