Введение в асимптотические методы. Лекция 4. Интегралы: нелокальные вклады

1. Введение в асимптотические методы. Лекция 4

нелокальные вклады
Интегралы:

2. 1. Локальные и глобальные вклады

До сих пор мы рассматривали интегралы, подобные
фигурирующим в лемме Ватсона, все члены в асимптотическом
разложении которых приходили из малой области некоторой точки.
Это, конечно, не есть общее правило.
Возможны ситуации, когда главный, либо следующие члены
асимптотического разложения, определяются вкладом всего
интервала интегрирования. Соответствующие вклады мы будем
называть глобальными, в отличие от локальных вкладов из
малых областей интервала интегрирования.
В данной лекции на простых примерах рассматривается техника
выделения различных вкладов.

3. 2. Пример 1

(
1
)
dx
1/ 2
= 2 ( 1 + e ) - e 1/2 ~ 2 - 2e 1/2 + e + K
e+x
0
Оценим, как произведение величины функции на длину интервала,
вклад в интеграл от области вблизи t = 0, где t µ e и от остальной части
интервала интегрирования.
I (e ) = ò
Локальный вклад
Глобальный вклад
xµe
( x +e )
x µ1
( x +e )
-1/ 2
µ e -1/ 2
-1/ 2
µ1
ò
ò
µ e -1/ 2 × e = e 1/ 2
µ 1 ×1 = 1
главный член дается глобальным вкладом, когда подынтегральная
функция может быть аппроксимирована как x -1/2, а интервал
интегрирования расположен между единицей и малой величиной,
находящейся вне e -окрестности нуля.
1
ò( x +e )
0
-1/ 2
1
dx :
-1/ 2
x
ò dx = 2
'0'

4. 3. Пример 1: метод вычитания

I (e ) = ò dt
1
e +t
Как искать следующие члены разложения? Метод вычитания:
0
1
ò( x +e )
-1/ 2
0
1
0
Локальный вклад
xµe
Глобальный вклад
x µ1
Победа локального.
ò( ( x +e )
1
0
-1/ 2
(
dx = 2 + ò ( x + e )
)
- x -1/ 2 dx
é( x + e ) -1/ 2 - x -1/ 2 ù µ e -1/ 2
ë
û
é( x + e ) -1/ 2 - x -1/ 2 ù µ e
ë
û
y = x/e
)
-1/ 2
ò
µ e -1/ 2 × e = e 1/ 2
ò
µ e ×1 = e
- перенормировка
'¥ '
(
- x -1/ 2 dx : e 1/ 2 ò ( 1 + y )
0
-1/ 2
)
- y -1/ 2 dy = -2e 1/ 2
С ростом числа удерживаемых в асимптотическом разложении
членов метод вычитания становится все более трудоемким

5. 4. Пример 1: метод расщепления

4. Пример 1: метод
dt
расщепления
I (e ) = ò
1
e +t
Иной подход основан на предварительном нахождении внешнего и
внутреннего асимптотических разложений подынтегральной функции.
Соответствующий метод называется методом расщепления интеграла.
0
Внешнее разложение t = O (1)
( e + t)
-1/ 2
=t
-1/ 2
(1+ e t)
1/ 2
=t
-1/ 2
æ 1 e 3e2
ö
1
+
+
K
ç
÷
2
è 2t 8t
ø
Внутреннее разложение t = t e = O (1)
-1/ 2
-1/ 2
( e + t ) = e -1/ 2 ( 1 + t )
Области применимости этих разложений перекрываются. Поэтому
можно определить некоторую условную границу t = d ( e = d = 1)
так, чтобы на интервалах ( 0, d ) и ( d ,1) работали внутреннее и
внешнее разложения.
d
1
Расщепляем интеграл на два I (e ) = I1 + I 2 = ò + ò
0
d

6. 5. Пример 1: метод расщепления

Для
вычисления I используем внешнее разложение
2
1
ò ( e + t)
-1/ 2
1
æ -1/ 2 e -3/ 2 3e 2 -5 / 2
dt : ò ç t
- t
+
t
+K
2
8
d è
ö
÷ dt =
ø
e 2 -3/ 2
= 2(1- d ) - e ( d
- 1) + ( d
- 1) + K
4
Для вычисления I1 используем внутреннее разложение
d
d
ò ( e + t)
0
-1/ 2
dt :
e
d /e
ò ( 1+t )
-1/ 2
(
dt =2e 1/ 2 ( 1 + d e )
0
= -2e
1/ 2
+ 2d
-1/ 2
1/ 2
1/ 2
(1+ e d )
1/ 2
= -2e
1/ 2
1/ 2
)
-1 =
+ 2d
Складывая их, получим четыре главных члена АР
I : 2 - 2e 1/ 2 + e - 14 e 2 +
1/ 2
+ ed
-1/ 2
e 2 -3/ 2
- d
+K
4
Подчеркнем, что все содержащие d члены в разложениях должны
были сократиться и сократились при суммировании.

7. 6. Пример 2

p /4
ò ( sin
2
x +e
)
2 -1
dx
0
Локальный вклад
Глобальный вклад
y = x/e
( sin 2 x + e 2 )
xµe
( sin
x µ1
p /4
ò ( sin
2
0
x +e
x+e
2
)
2 -1
-1
)
2 -1
µ1
'¥'
dx :
ò
ò
µ e -2
ò (e
2
y +e
2
)
µ e -1
µ1
2 -1
e dy =
0
p
2e
Поправочный член приходит от глобального вклада
Можно проверить это устраивая вычитание как в примере 1.
Другая возможность:
1
1
1
=
=
=
sin 2 x + e 2 sin 2 ( e y ) + e 2 e 2 + e 2 y 2 - 13 e 4 y 4 +K
æ
1 ç 1
e 2 y4
= 2
+
+K
e ç 1+ y2 3( 1 + y2 ) 2
è
ö
÷
÷
ø
Этот интеграл расходится из-за поведения
на ' ¥ ', т.е. вовне интервала y µ 1
Это указывает на глобальность вклада в
поправочном члене.

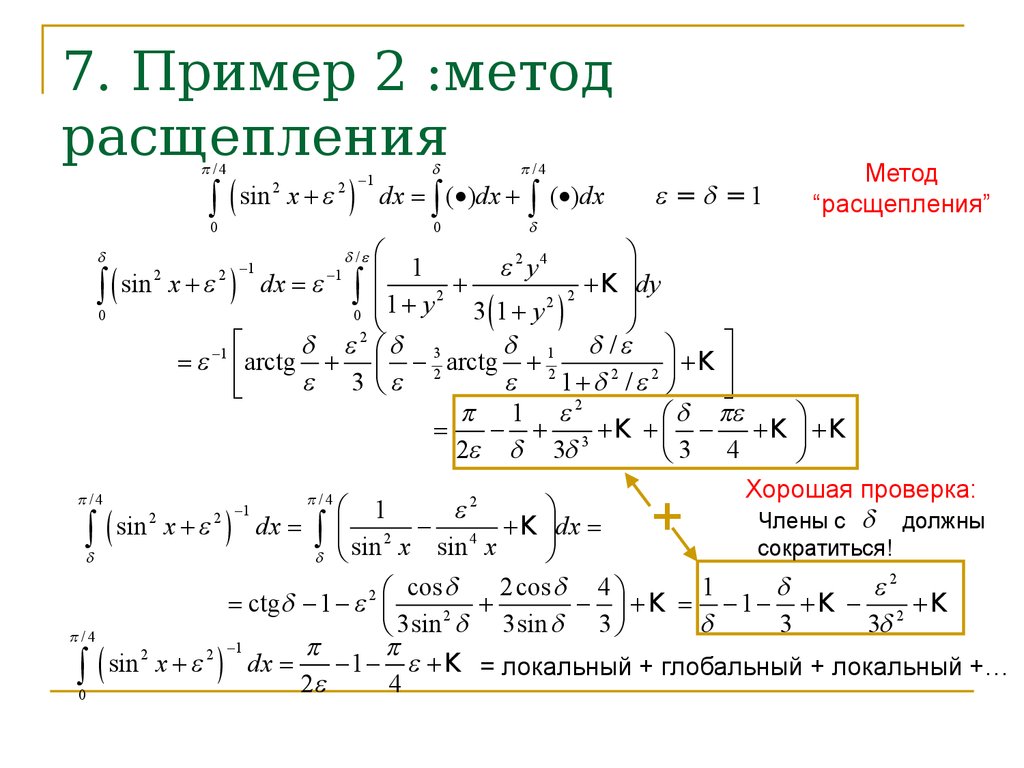
8. 7. Пример 2 :метод расщепления

p /4
ò ( sin
2
x +e
)
2 -1
0
d
p /4
0
d
dx = ò (·)dx +
ò (·)dx
e = d =1
Метод
“расщепления”
æ
ö
2 4
1
e
y
2
-1
ò0 ( sin x + e ) dx = e ò0 çç 1 + y 2 + 3 1 + y 2 2 + K ÷÷dy
(
)
è
ø
2
é
ù
d e æd 3
d 1 d /e ö
-1
= e êarctg + ç - 2 arctg + 2
+K ú
2
2 ÷
e
3
e
e
1
+
d
/
e
è
ø
ë
û
2
p 1 e
æ d pe
=
- + 3 +K + ç +K
2e d 3d
è3 4
d
d /e
2 -1
p /4
p /4
+
ö
÷ +K
ø
Хорошая проверка:
Члены с d должны
æ 1
ö
e2
sin
x
+
e
dx
=
+
K
)
òd (
òd çè sin 2 x sin 4 x ÷ødx =
сократиться!
2 cos d 4 ö
1
d
e2
2 æ cos d
= ctgd - 1 - e ç
+
- ÷ +K = -1- +K - 2 +K
2
d
3
3d
è 3sin d 3sin d 3 ø
p /4
1
p
p
2
2
sin
x
+
e
dx
=
1
e + K = локальный + глобальный + локальный +…
(
)
ò0
2e
4
2
2 -1

9. 8. Пример 3: Логарифмы

Наиболее сложна промежуточная ситуация – когда основной вклад в
интеграл не локальный и не глобальный.
¥
1
I (e ) = ò f ( x; e ) dx
f ( x; e ) =
( x + e )a (1 + x)
0
¥
dx
I (e ) : ò a
a <1
Победа глобального
x (1 + x)
'0'
'¥ '
dx
I
(
e
)
:
Победа локального
a >1
ò0 (e + x)a
I:1
f : e -1
x: e
Локальный вклад
Ничья
a =1
I
:
1
f :1
x: 1
Нелокальный вклад
Здесь основной вклад – из зазора
e = x =1
I (e ) : ln(1/ e ) + O(1)
Корректирующий член всего лишь в O ( 1/ ln(1/ e ) ) раз меньше основного,
и его надо вычислять, если e не о-о-о-чень уж мало. e = 10-4 , 1/ ln ( 1/ e ) = 0.11
(
)

10. 9. Интегральное уравнение: Электрическая емкость тонкого тела

9. Интегральное уравнение:
Электрическая емкость
r
1
q( z¢; e ) dz¢
тонкого
тела
j
(
r
,
z
;
e
)
=
r = e R( z )
Dj = 0, j (¥) = 0
ò
1
4p
z
-1
j =1
+1
1
1=
4p
-1
r 2 + ( z - z¢)
q( z ¢; e )dz ¢
1
ò
-1
e R ( z ) + ( z - z¢)
2
2
2
2
(1)
Для нахождения электрической емкости
1
C = ò q ( z ¢; e ) dz ¢
-1
необходимо решить интегральное уравнение (1)
Интегральные уравнения требуют привлечения как техники решения
алгебраических уравнений, так и техники асимптотического анализа
интегралов

11. 10. Интегральное уравнение: оценка интегралов

1
q( z¢; e ) dz¢
1
1=
4p
ò
-1
e 2 R 2 ( z ) + ( z - z¢)
2
В первую очередь нужно асимптотически исследовать интеграл
1
q ( z¢; e ) dz ¢
= I1 + I 2 ,
ò-1 2 2
2
e R ( z ) + ( z - z ¢)
I1 = q ( z ; e )
ò
-1
I2 =
dz ¢
1
e R ( z ) + ( z - z ¢)
2
2
2
= ln
z +1+
z -1+
( z + 1) + e 2 R 2 ( z )
2
( z - 1) + e 2 R 2 ( z )
1
( q ( z¢; e ) - q ( z; e ) ) dz¢
Если z - z ¢ µ e ,
-1
e 2 R 2 ( z ) + ( z - z ¢)
Если z - z¢ µ 1,
ò
2
1
I2 :
ò
-1
2
f µ 1,
f µ 1,
( q ( z¢; e ) - q ( z; e ) ) dz¢ + O ( e )
z - z¢
ò
ò
2 1 - z2
= 2q( z ) ln
+O(e2)
e R( z )
µ 1 × e = e Победа
µ 1 × 1 = 1 глобального

12. 11. Интегральное уравнение: итерации

¢
( q( z ) - q( z ) ) dz¢
2 1 - z2
4p = 2q( z ) ln
+ò
e R ( z ) -1
z - z¢
1
q = 2p ( ln e
)
-1 -1
(
+ O ( ln e
O ( 1)
Чтобы найти следующие члены разложения удобно воспользоваться
методом итераций
1
2p
æ 2 1 - z2 ö
æ
ö
1 ( q( z¢) - q( z ) )
q
(
z
)
=
0
q( z ) = 2p ç 1 dz ¢ ÷ ln ç
÷
1
ò
ç
÷
¢
ln
4
p
z
z
e
R
(
z
)
-1
è
ø
è
ø
e
-3
ææ 1 ö ö
2p ( 1 - 0 )
2p
2p
R( z )
q1 ( z ) =
=
+
ln
+
O
çç ç ln ÷ ÷÷
2
2
2
1
æ 2 1 - z ö ln
è eø ø
2 1- z
æ 1ö
è
ln
ln ç
÷
e çè e ÷ø
ç e R( z ) ÷
è
ø
1
æ æ 1 ö -3 ö
4p
2p
R( z )
C=
+
ln
+ O ç ç ln ÷ ÷
çè e ø ÷
1 æ 1 ö 2 -ò1 2 1 - z 2
è
ø
ln
ln
ç
÷
e è eø
2q ln ( 1/ e )
)
-1 -2
)

13. 12. Интегральное уравнение: эллипсоиды

2 1 - z ( q( z¢) - q( z))
4p = 2q( z ) ln
2
e R( z )
1
+ò
-1
z - z¢
dz ¢
(1)
В ряде случаев точность можно существенно улучшить. Это
относится, например, к эллипсоидам вращения R = 1 - z 2 При этом
первый член в правой части (1) есть константа, поэтому константой
оказывается и решение уравнения (1).
2p
4p
q( z ) =
+O(e2) , C =
+O(e2)
æ2ö
ln ç ÷
èe ø
æ2ö
ln ç ÷
èe ø
Здесь, по существу, нам удалось полностью просуммировать ряд по
степеням ln - k ( 1/ e )
1
4p
2p
R( z )
C=
1
ln
e
+
æ 1ö
ç ln ÷
è eø
2
ò ln 2
-1
1- z
2
+K
принципиально улучшив таким образом асимптотическое разложение

14. 13. Интегральное уравнение: выводы

Из проведенного исследования следуют два интересных
физических феномена.
1. Слабая зависимость емкости длинного тонкого тела от формы
его поперечного сечения. Более того, емкость слабо зависит и
от толщины тела. Скажем, при изменении e вдвое она
изменится не в главном, но лишь в следующем члене.
2. Емкость длинного тонкого тела оказывается аномально
большой по сравнению с телами, имеющими размеры одного
порядка по всем направлениям. К примеру шар того же объема
2/3
2
( : e ) имеет емкость (пропорциональную радиусу) : e-1 , что
много меньше емкости длинного тонкого тела : ( ln e -1 )
Фильтрационная аналогии: скважина намного лучше, чем сферическая
полость того же объема. Правда еще лучше тонкое блинообразное
тело того же объема. Попробуйте проверить!

15. 14. Упражнения к лекции 4

1.
Вычислить первые два члена при r ® 0 и первые четыре члена
при r ® ¥ асимптотических разложений интеграла
¥
rx
ò0 r 2 + x 3/ 2 ( 1 + x ) dx
(
2.
3.
Рассмотреть интеграл
)
1
ln x
ò0 e + x dx
Найти 2 члена асимптотического разложения при m ® 1 - 0
p /2
dq
эллиптического интеграла
ò
1 - m 2 sin 2 q
Функция q( z ) удовлетворяет интегральному уравнению
1
q ( z¢; e ) dz ¢
ò-1 e 2 + ( z - z¢) 2 = z, z £ 1
Найти два главных члена ее асимптотического представления
0
4.