Основные законы распределения, применяемые при обработке данных научного эксперимента. (Лекция 2)

1. Лекция 3: Основные законы распределения, применяемые при обработке данных научного эксперимента

1.
2.
3.
4.
5.
Нормальное распределение
Равномерное распределение
Логарифмически нормальное распределение
Экспоненциальное распределение
Распределение Вейбулла
Учебно-исследовательская работа
студента. Лекция 2
1

2. 1 Нормальное распределение N(μ, σ)

Один из основных законов распределения в прикладной
математической статистике. Во многом это следствие ЦПТ.
ЦПТ:
ЦПТ распределение суммы независимых случайных
величин с любым исходным распределением будет
нормальным, если число слагаемых достаточно велико, а
вклад каждого в сумму – мал.
ЦПТ соответствует многим реальным физическим
процессам.
При возрастании объема выборки большинство
распределений стремится к нормальному => N(μ, σ) может
быть использовано для аппроксимации таких
распределений.
Учебно-исследовательская работа
студента. Лекция 2
2

3.

Примеры применения N(μ, σ):
•распределение погрешности измерений (кроме приборной
погрешности);
•в теории распространения радиоволн для описания
мерцания ‑ флуктуаций параметра относительно его
среднего значения;
•в неявном виде для описания параметра, представленного
в логарифмическом масштабе (заменяя явный вид
логнормального распределения);
•в теории надежности для описания износовых отказов,
интенсивность которых со временем возрастает (обычно)
Учебно-исследовательская
работа студента. Лекция 2
3

4.

Свойства N(μ, σ):
Обозначение
Параметры
Плотность
Функция
распределения
Мат. ожидание
Дисперсия
Коэффициент
асимметрии
Коэффициент
эксцесса
Мода
Медиана
N(μ, σ)
μ, σ
1 x 2
1
f x; ,
exp
2
2
x
1 t 2
1
dt
F x; ,
exp
2
2
M x
D x 2
a3=0
a4=0 («сдвинутый» на 3)
Mo=μ
Me=μ
Учебно-исследовательская
работа студента. Лекция 2
4

5.

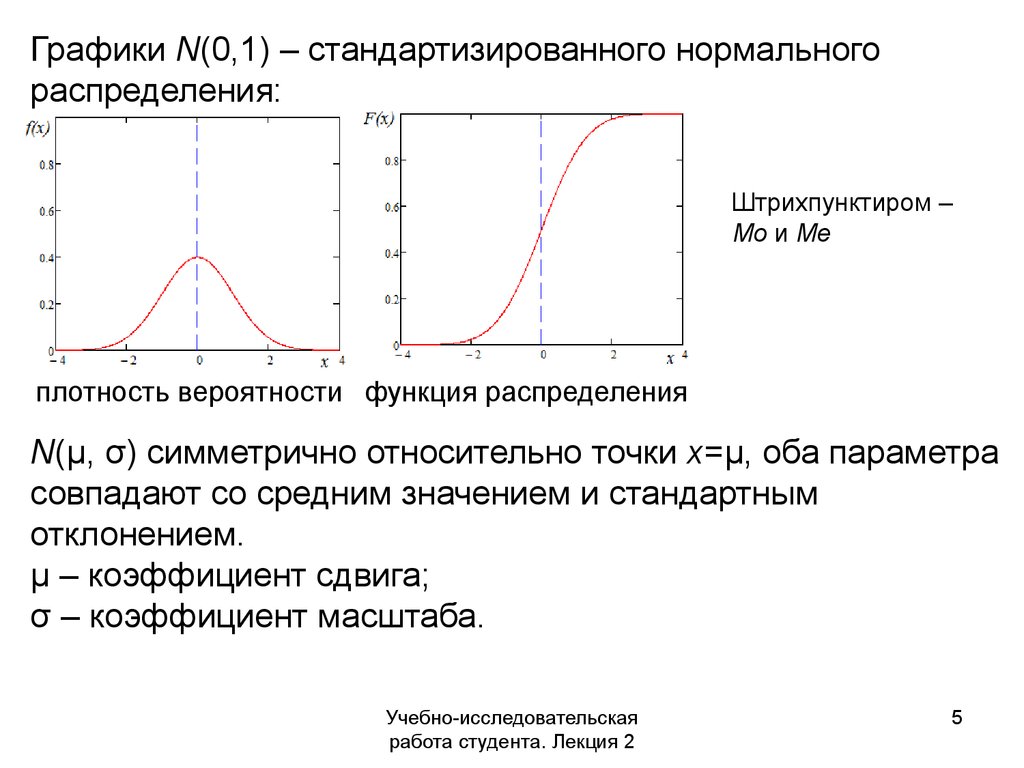
Графики N(0,1) – стандартизированного нормального
распределения:
Штрихпунктиром –
Mo и Me
плотность вероятности функция распределения
N(μ, σ) симметрично относительно точки x=μ, оба параметра
совпадают со средним значением и стандартным
отклонением.
μ – коэффициент сдвига;
σ – коэффициент масштаба.
Учебно-исследовательская
работа студента. Лекция 2
5

6.

Значения F(x) распределения N(0,1) приводятся в
справочниках виде таблиц.
Также приводятся таблицы значений функции (интеграла)
Лапласа
z 2 F z 1,
Для N(0,1)
z
x
F z 1 F z
Квантиль up нормально распределенной случайной
величины N(μ, σ) связан с квантилью случайной величины,
имеющей стандартное нормальное распределение N(0,1),
upc, соотношением up=μ+ upc. Значения квантиля upc задается
таблично.
Учебно-исследовательская
работа студента. Лекция 2
6

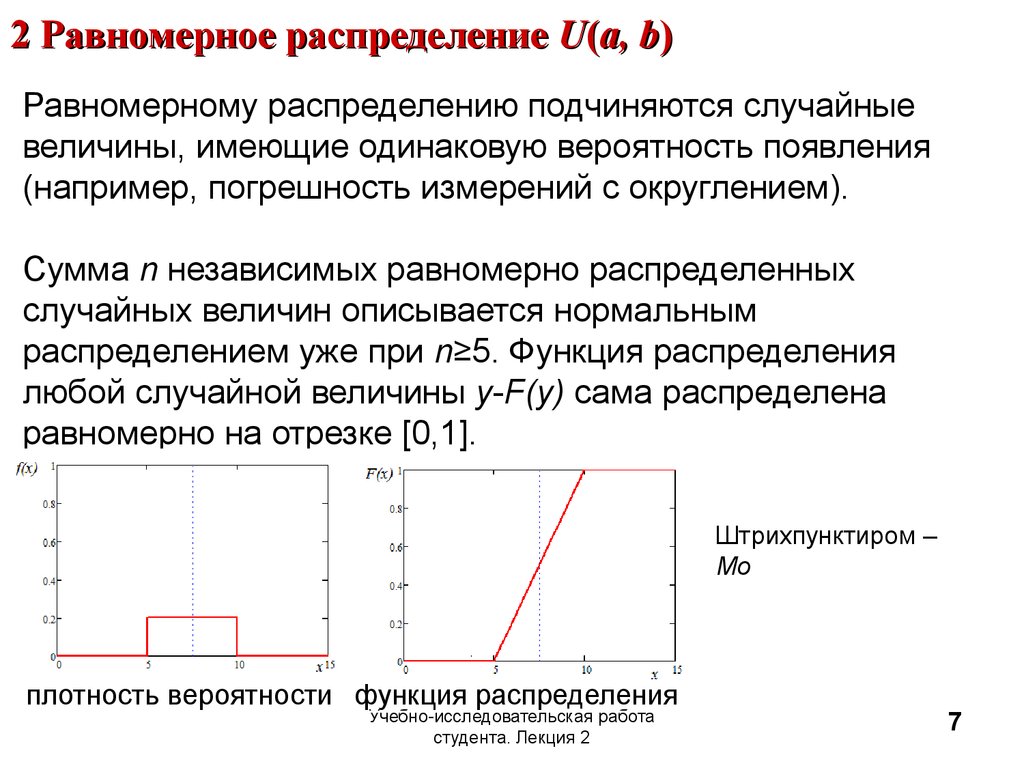
7. 2 Равномерное распределение U(a, b)

Равномерному распределению подчиняются случайные
величины, имеющие одинаковую вероятность появления
(например, погрешность измерений с округлением).
Сумма n независимых равномерно распределенных
случайных величин описывается нормальным
распределением уже при n≥5. Функция распределения
любой случайной величины y-F(y) сама распределена
равномерно на отрезке [0,1].
Штрихпунктиром –
Mo
плотность вероятности функция распределения
Учебно-исследовательская работа
студента. Лекция 2
7

8.

Свойства U(a, b):
Обозначение
Параметры
Плотность
Функция
распределения
Мат. ожидание
Дисперсия
К-т асимметрии
К-т эксцесса
Мода
Медиана
U(a, b)
a, b
1
, a x b
f ( x; a, b) b a
0,
x a; x b
x a
0,
x a
F ( x; a, b)
,
a x b
b a
x b
1,
M x 0,5 b a
b a 2
D x
a3=0
a4=-1,2
12
b a
Mo
M x
2
Учебно-исследовательская
работа студента. Лекция 2
не определена
8

9. 3 Логарифмически нормальное распределение LN(μ, σ)

Если сл.в. Y распределена нормально, то сл.в. x=ln(Y)
подчинена логарифмически нормальному (логнормальному)
закону распределения.
Значения логнормальной случайной величины формируются
под воздействием очень большого числа взаимно
независимых факторов:
•воздействие каждого отдельного фактора «равномерно
незначительно» и равновероятно по знаку;
•прирост, вызываемый действием каждого следующего
фактора, пропорционален уже достигнутому к этому
моменту значению исследуемой величины.
Учебно-исследовательская
работа студента. Лекция 2
9

10.

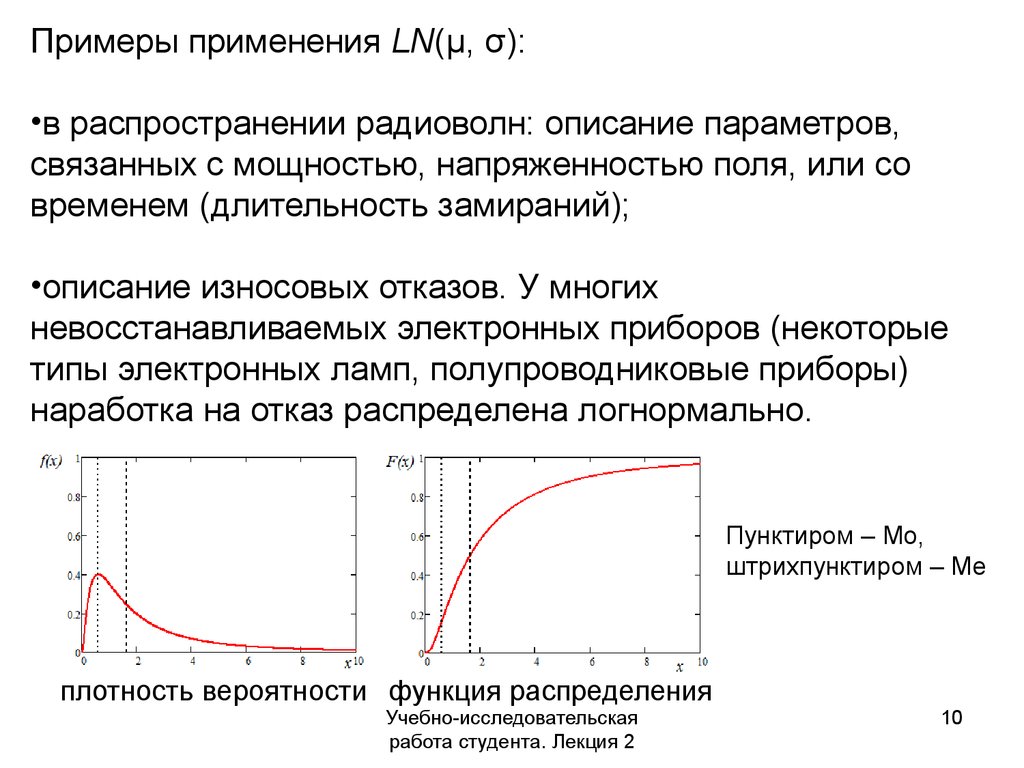
Примеры применения LN(μ, σ):
•в распространении радиоволн: описание параметров,
связанных с мощностью, напряженностью поля, или со
временем (длительность замираний);
•описание износовых отказов. У многих
невосстанавливаемых электронных приборов (некоторые
типы электронных ламп, полупроводниковые приборы)
наработка на отказ распределена логнормально.
Пунктиром – Mo,
штрихпунктиром – Me
плотность вероятности функция распределения
Учебно-исследовательская
работа студента. Лекция 2
10

11.

Свойства LN(μ, σ):
Обозначение
Параметры
Плотность
Функция
распределения
Мат. ожидание
Дисперсия
Коэффициент
асимметрии
Коэффициент
эксцесса
Мода
Медиана
LN(μ, σ)
μ, σ
1 ln x 2
f x; ,
exp
2
x 2
2
x
1
1 ln t
F x; ,
exp
dt
x 2
2
M x exp 0,5 2
1
2
D x exp 2 e 1
0, 5
2
2
a3 e 1 e 2
2
2
3 2
2 2
a4 3 e 1 e 3e
6 3
Mo exp 2
Me e
Учебно-исследовательская
работа студента. Лекция 2
11

12.

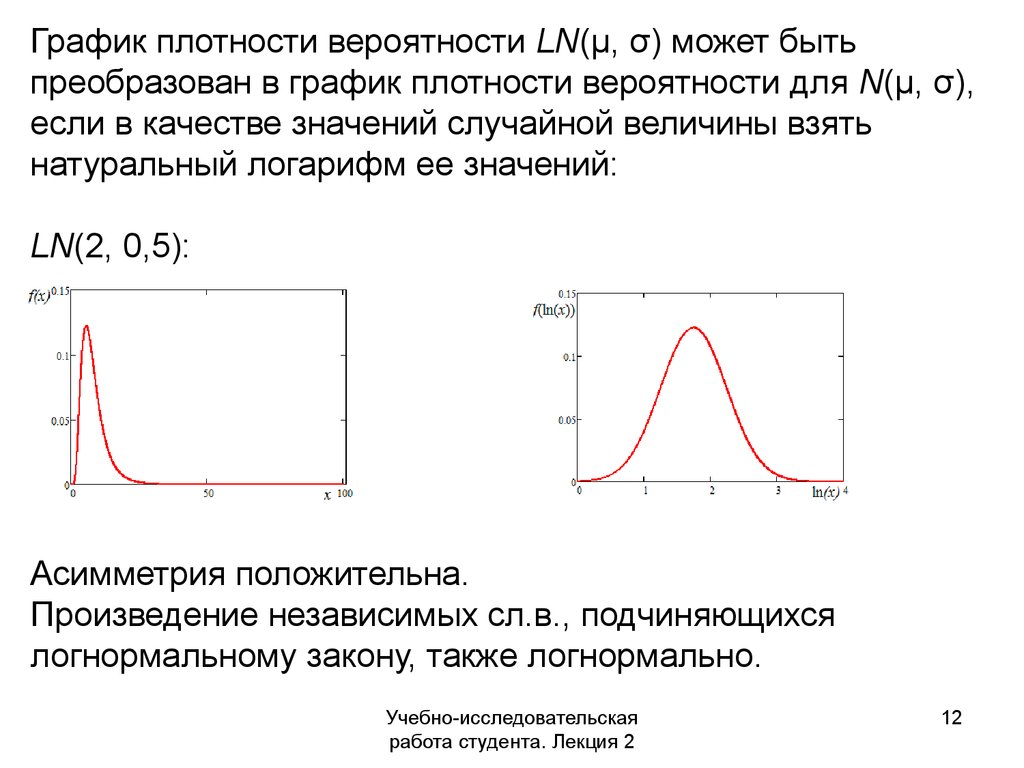
График плотности вероятности LN(μ, σ) может быть
преобразован в график плотности вероятности для N(μ, σ),
если в качестве значений случайной величины взять
натуральный логарифм ее значений:
LN(2, 0,5):
Асимметрия положительна.
Произведение независимых сл.в., подчиняющихся
логнормальному закону, также логнормально.
Учебно-исследовательская
работа студента. Лекция 2
12

13. 4 Экспоненциальное распределение Exp(b)

Одно из наиболее часто встречающихся распределений в
теории надежности.
Примеры использования:
•описание внезапных отказов, когда износом изделия можно
пренебречь;
•наработка на отказ многих невосстанавливаемых изделий;
•наработка на отказ между соседними отказами у
восстанавливаемых изделий в случае простейшего потока;
•наработка на отказ большой многокомпонентной системы
при любом распределении наработки на отказ компонентов
системы.
Учебно-исследовательская
работа студента. Лекция 2
13

14.

Свойства Exp(b):
Обозначение
Параметры
Плотность
Exp(b)
b
1
x
f x; b exp , x 0
b
b
Функция
распределения
x
F x; b 1 exp , x 0
b
Мат. ожидание
b
Дисперсия
b2
Коэффициент
асимметрии
Коэффициент
эксцесса
Мода
Медиана
2
9
0
b ln2
Учебно-исследовательская
работа студента. Лекция 2
14

15.

Штрихпунктиром – Me
плотность вероятности функция распределения
b – коэффициент масштаба.
Экспоненциальное распределение – частный случай
распределения Вейбулла. Отличительная особенность –
постоянство интенсивности отказов λ=1/b=const – в теории
надежности интерпретируется как независимость
вероятности отказа от наработки, что эквивалентно
отсутствию износа.
Учебно-исследовательская
работа студента. Лекция 2
15

16. 5 Распределение Вейбулла W(α, β, μ)

Используется при многих расчетах надежности.
Распределению Вейбулла подчиняется наработка на отказ
многих невосстанавливаемых электронных приборов,
например, электронных ламп, полупроводниковых приборов,
некоторых приборов СВЧ.
Имеет три параметра, однако часто говорят либо о двух
(μ=0), либо об одном – параметре β.
Смысл параметров:
α – параметр масштаба;
β – параметр формы;
μ – параметр сдвига.
Учебно-исследовательская
работа студента. Лекция 2
16

17.

Свойства W(α, β, μ):
Плотность вероятности
x
x 1 exp
, x ;
f x; , ,
x .
0,
Функция распределения
x
, x ;
1 exp
F x; , ,
x .
0,
Учебно-исследовательская
работа студента. Лекция 2
17

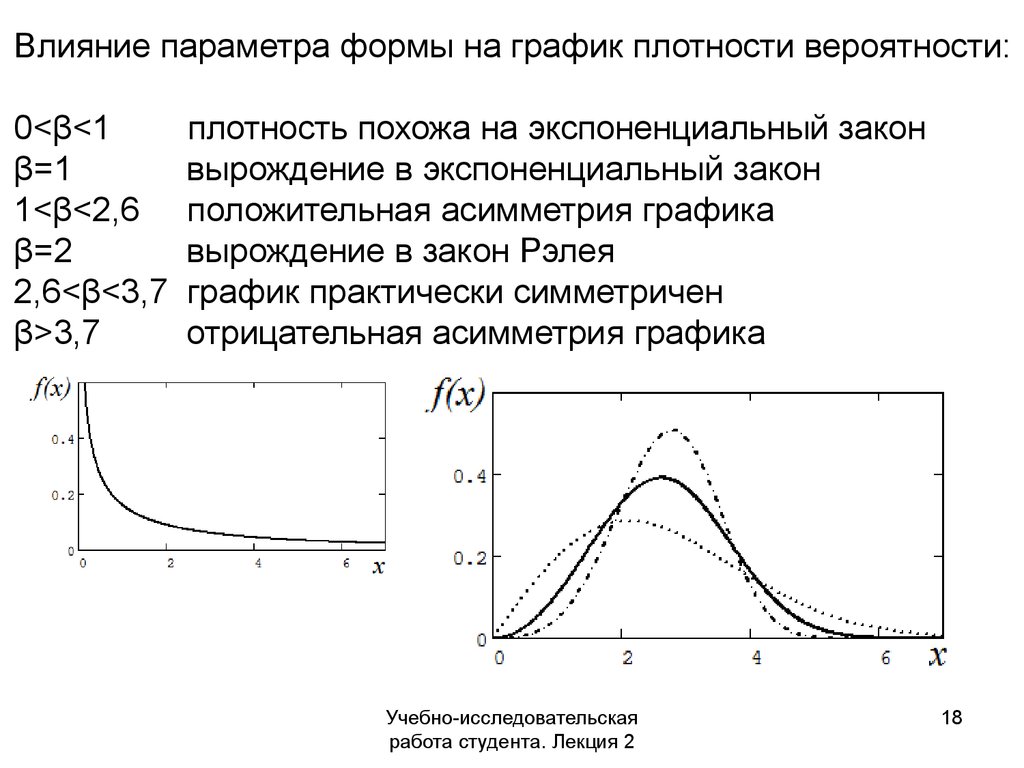
18.

Влияние параметра формы на график плотности вероятности:
0<β<1
β=1
1<β<2,6
β=2
2,6<β<3,7
β>3,7
плотность похожа на экспоненциальный закон
вырождение в экспоненциальный закон
положительная асимметрия графика
вырождение в закон Рэлея
график практически симметричен
отрицательная асимметрия графика
Учебно-исследовательская
работа студента. Лекция 2
18