Похожие презентации:
Тераэдр, параллелепипед
1.
Тетраэдри
параллелепипед
2.
ТетраэдрПоверхность,
составленная из четырёх
треугольников ABC,
DAB, DBC и DCA,
называется тетраэдром
(DABC).
Тетра́эдр —многогранник,
гранями которого являются
четыре треугольника.
3.
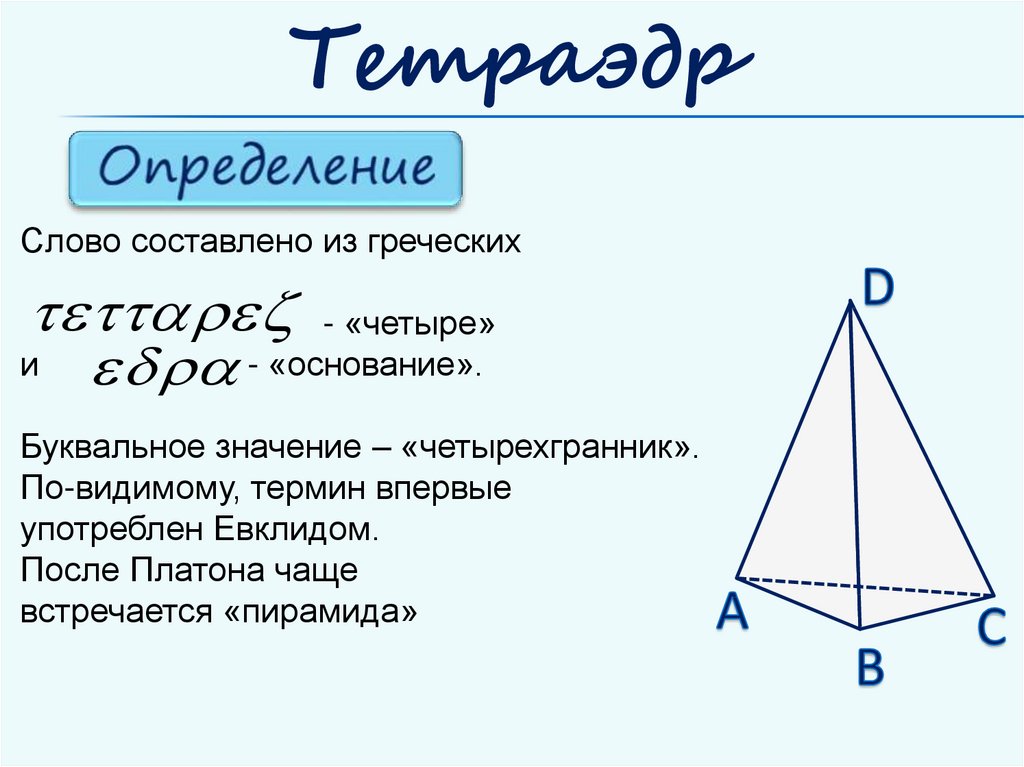
ТетраэдрСлово составлено из греческих
- «четыре»
и - «основание».
Буквальное значение – «четырехгранник».
По-видимому, термин впервые
употреблен Евклидом.
После Платона чаще
встречается «пирамида»
4.
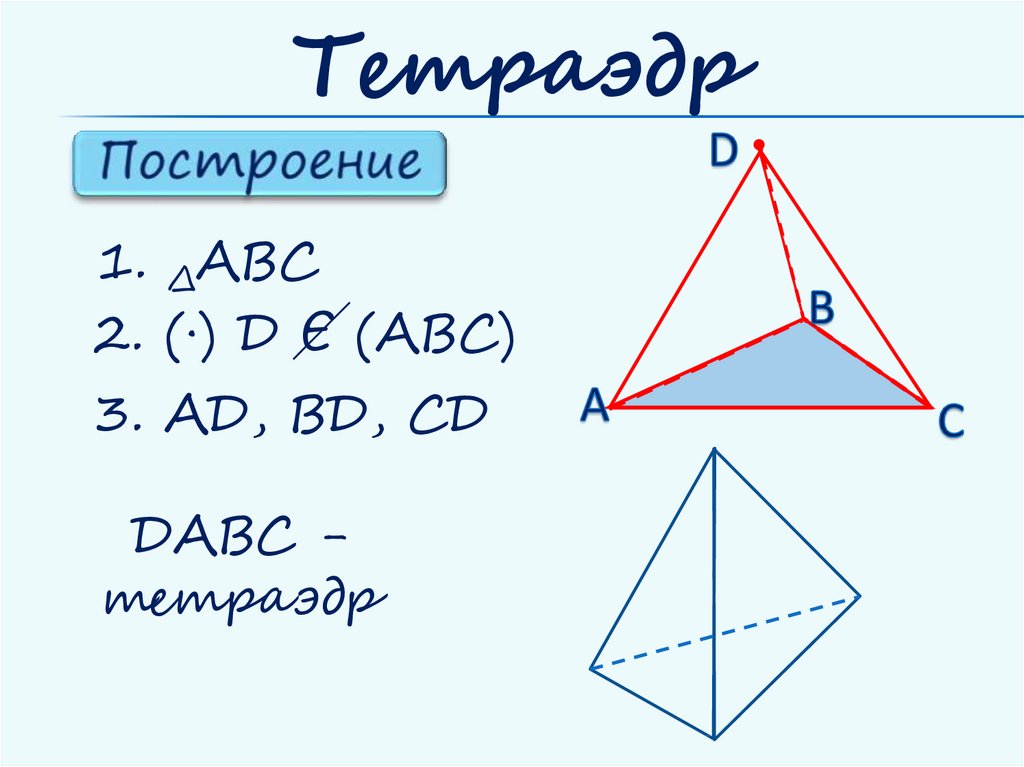
Тетраэдр1. ∆АВС
2. (∙) Д Є (АВС)
3. АД, ВД, СД
ДАВС тетраэдр
5.
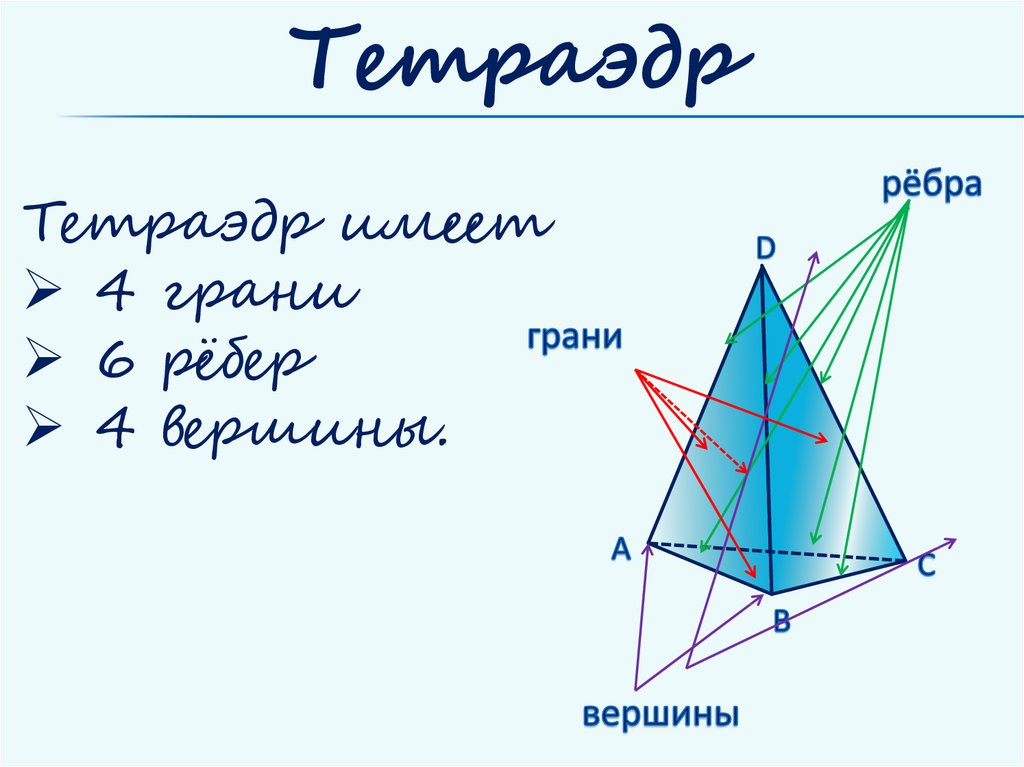
ТетраэдрТетраэдр имеет
4 грани
6 рёбер
4 вершины.
6.
ПараллелепипедПоверхность, составленная из
двух равных
параллелограммов ABCD и
A1B1C1D1 и четырёх
параллелограммов ABB1A1,
BCC1B1, CDD1C1 и DAA1D1,
называется параллелепипедом
ABCDA1B1C1D1.
В1
С1
A1
Параллелепипед —
многогранник, гранями
которого являются
A
параллелограммы.
D1
В
C
D
7.
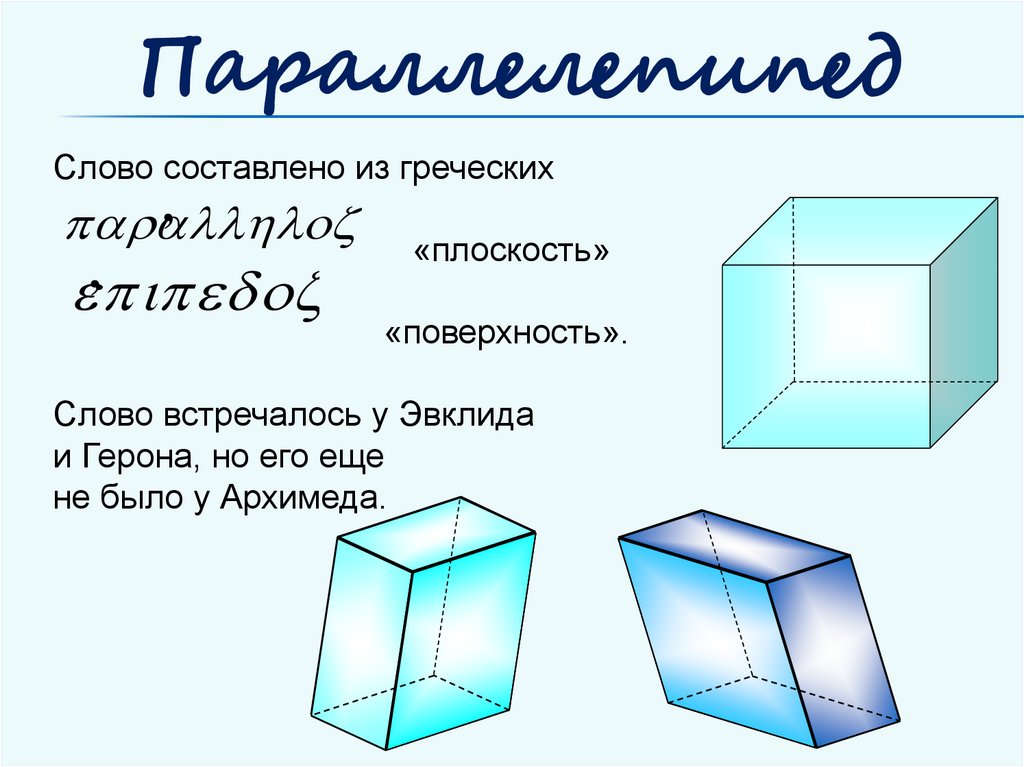
ПараллелепипедСлово составлено из греческих
,
,
«плоскость»
«поверхность».
Слово встречалось у Эвклида
и Герона, но его еще
не было у Архимеда.
8.
Видыпараллелепипедов
Параллелепипеды
наклонные
прямые
прямоугольные
куб
9.
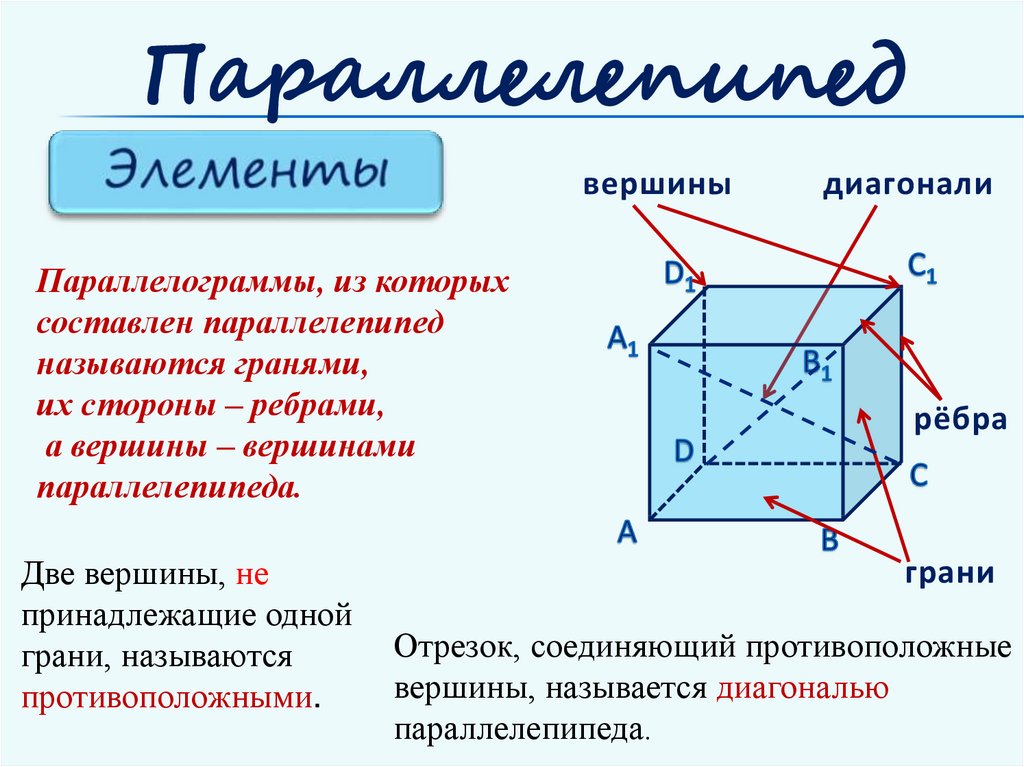
Параллелепипедвершины
Параллелограммы, из которых
составлен параллелепипед
называются гранями,
их стороны – ребрами,
а вершины – вершинами
параллелепипеда.
Две вершины, не
принадлежащие одной
грани, называются
противоположными.
диагонали
рёбра
грани
Отрезок, соединяющий противоположные
вершины, называется диагональю
параллелепипеда.
10.
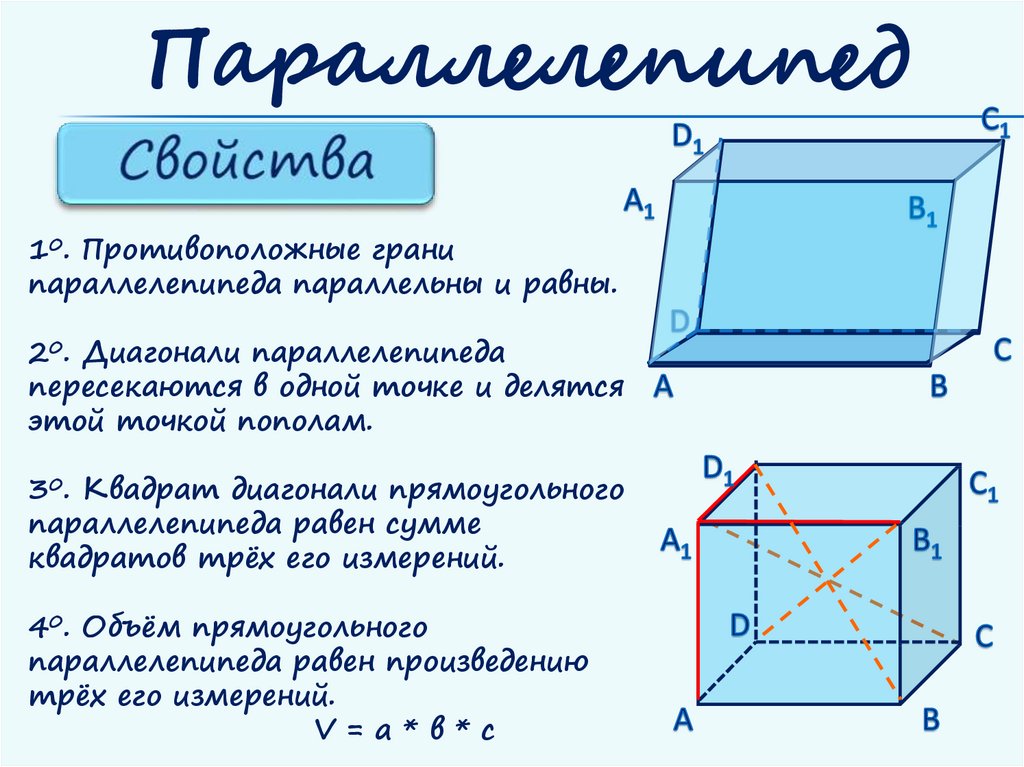
Параллелепипед10. Противоположные грани
параллелепипеда параллельны и равны.
20. Диагонали параллелепипеда
пересекаются в одной точке и делятся
этой точкой пополам.
30. Квадрат диагонали прямоугольного
параллелепипеда равен сумме
квадратов трёх его измерений.
40. Объём прямоугольного
параллелепипеда равен произведению
трёх его измерений.
V=а*в*с




 Математика
Математика








