Приближение сплайнами

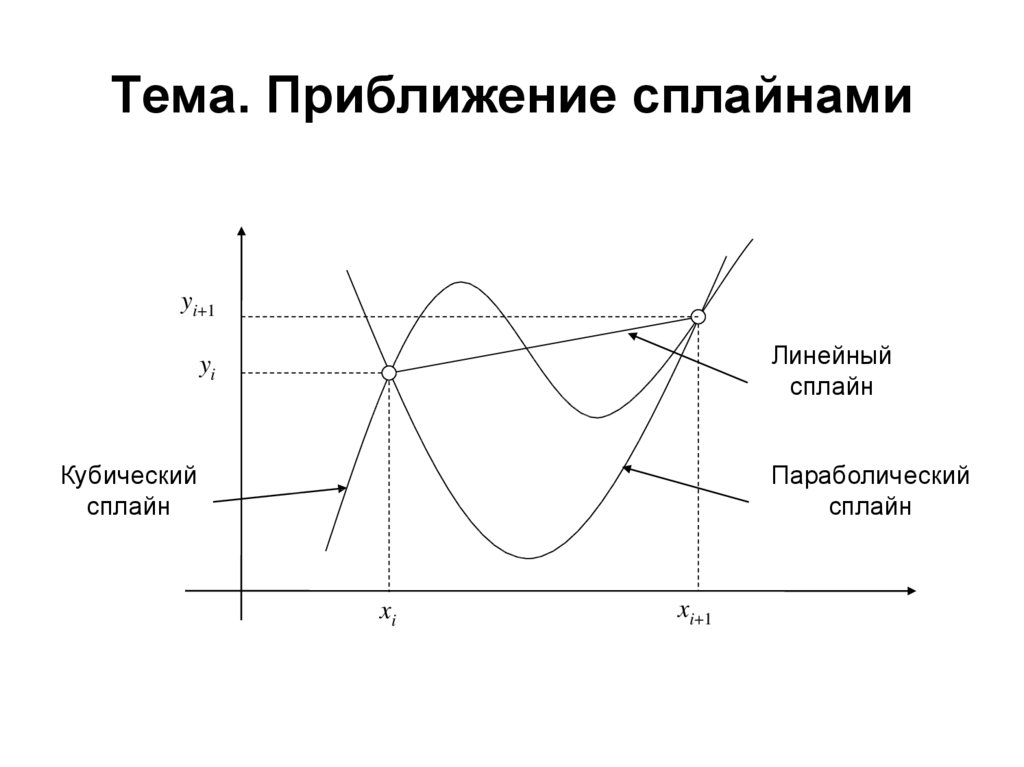
1. Тема. Приближение сплайнами

yi+1
Линейный
сплайн
yi
Кубический
сплайн
Параболический
сплайн
xi
xi+1

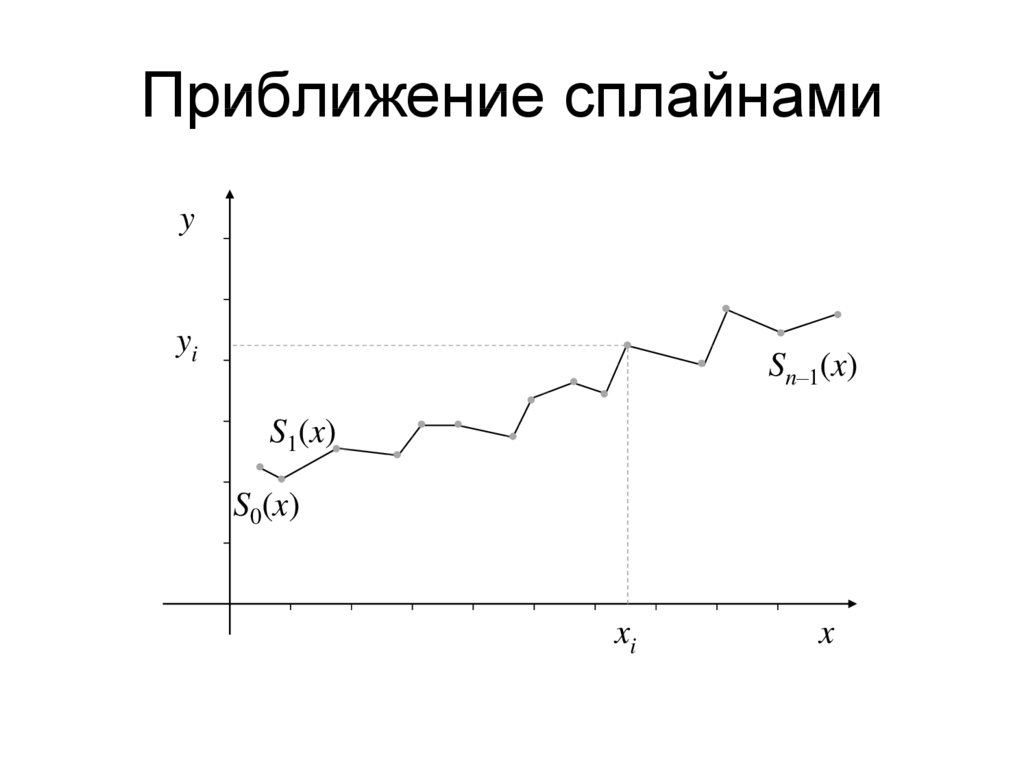
2. Приближение сплайнами

y
yi
Sn–1(x)
S1(x)
S0(x)
xi
x

3. Приближение сплайнами

Постановка задачи.
Сетка (табличные значения функции):
{xi}: i = 0, 1, …, n
{yi}: yi = f (xi)
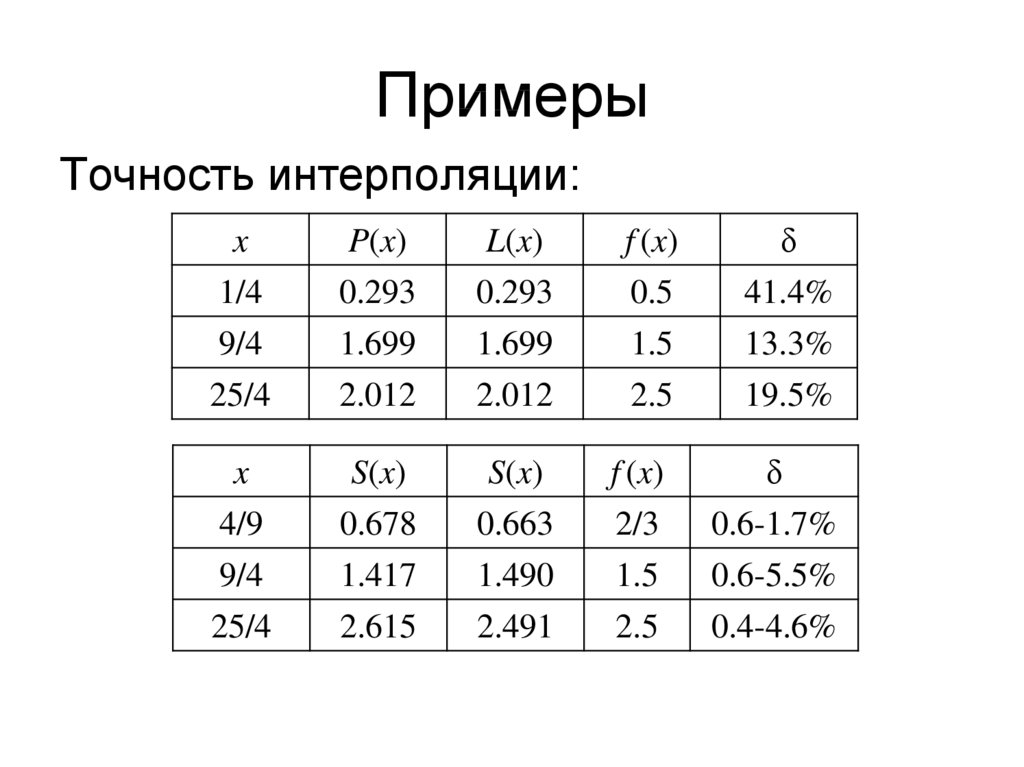
Количество узлов – n + 1. Количество
сплайнов – n: S0(x), S1(x), …, Sn–1(x). Для
Si(x) область действия x [xi, xi+1].

4. Приближение сплайнами

Постановка задачи.
m
Si x c ji ji x , ji x x xi
j
j 0
m
Si x c ji x xi , i 0,1,..., n 1, m 1, 2,3
j
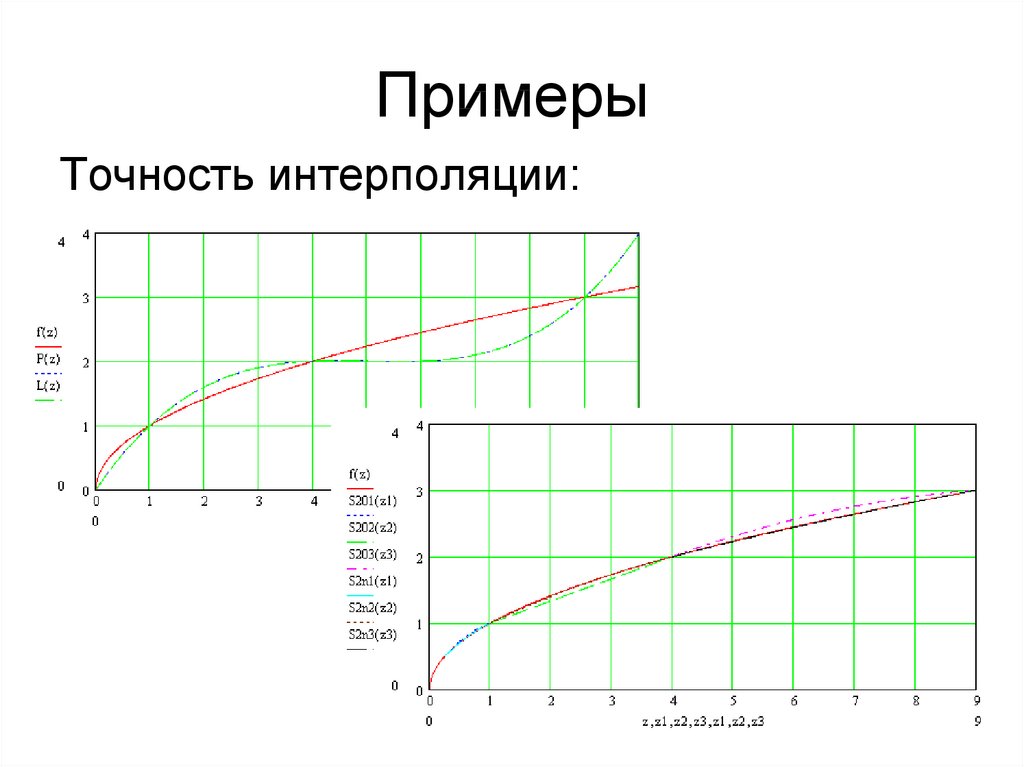
j 0
ai = c0i, bi = c1i, ci = c2i, di = c3i
При m > 1 требуются граничные условия.

5. Линейные сплайны

m = 1:
Si x ai bi x xi , i 0,1,..., n 1
Si xi 1 Si 1 xi 1 , i 0,1,..., n 2
yi
ai yi , bi
xi
Здесь ∆xi = xi+1 – xi, ∆yi = yi+1 – yi.

6. Параболические сплайны

m = 2:
Si x ai bi x xi ci x xi , i 0,1,..., n 1
2
Si xi 1 Si 1 xi 1 ,
Si xi 1 Si 1 xi 1 , i 0,1,..., n 2
Граничные условия:
1. A0 = f (x0);
2. An = f (xn).

7. Параболические сплайны

bi 1 bi
ai yi , ci
.
2 xi
Если A0 = f (x0), то
2 yi
b0 A0 , bi 1
bi , i 0,1,..., n 2.
xi
Если An = f (xn), то
2 yi
bn An , bi
bi 1 , i n 1, n 2,..., 0.
xi

8. Кубические сплайны

m = 3:
Si x ai bi x xi ci x xi di x xi , i 0,1,..., n 1
2
3
Si xi 1 Si 1 xi 1 , Si xi 1 Si 1 xi 1 ,
Si xi 1 Si 1 xi 1 , i 0,1,..., n 2
Граничные условия:
1. A0 = f (x0), An = f (xn);
2. B0 = f (x0), Bn = f (xn).

9. Кубические сплайны

ai yi ,
yi xi
bi
2M i M i 1 ,
xi
6
1
ci M i ,
2
M i 1 M i
di
, i 0,1,..., n 1.
6 xi

10. Кубические сплайны

Если A0 = f (x0), An = f (xn), то
b0 = A0, bn = An
AM g
x0
xn 1
a00 3 ; ann 3 ;
1
A a jj x j 1 x j , j 1, 2,..., n 1;
3
1
a j , j 1 a j 1, j 6 x j , j 0,1,..., n 1

11. Кубические сплайны

Если A0 = f (x0), An = f (xn), то
b0 = A0, bn = An
AM g
y0
yn 1
g 0 x A0 ; g n An x ;
0
n 1
g
g yi yi 1 , i 1, 2,..., n 1
i xi xi 1
M = (M0, M1, M2, …, Mn)

12. Кубические сплайны

Если B0 = f (x0), Bn = f (xn), то
M0 = B0, Mn = Bn
AM g
M = (M1, M2, …, Mn–1)
1
a jj a jj 3 x j 1 x j , j 1, 2,..., n 1;
A
1
a
x j , j 1, 2,..., n 2
j , j 1 a j 1, j a j , j 1 a j 1, j
6

13. Кубические сплайны

Если B0 = f (x0), Bn = f (xn), то
M0 = B0, Mn = Bn
AM g
yi yi 1
gi gi 1 n 1
1 n 1 , i 1, 2,..., n 1,
xi xi 1
x0
xn 1
B0 , i 1
Bn , i n 1
1 6
; n 1 6
0, i 1
0, i n 1

14. Примеры

Параболический сплайн.
f x x
i
x
y
0
1/4
1/2
1
1
1
2
4
2
3
9
3
Результирующая сетка: {4/9, 9/4, 25/4}
Граничные условия: f x
1
1
A0 1, A3
6
2 x
Далее строим сплайны S0(x), S1(x), S2(x).

15. Примеры

i
x
y
1
x0 1
4
1
y0 1
2
0
1/4
1/2
1
1
1
2
4
2
3
9
3
3
; x1 4 1 3; x2 9 4 5;
4
1
; y1 2 1 1; y2 3 2 1
2
2 y0
2 y1
2 1 2
1
b0 1, b1
b0
1 , b2
b1
x0
34
3
x1
2 y2
2 1 1 1
2 1 1 1
, b3
b2
3 3 3
x2
5 3 15

16. Примеры

i
x
y
1
x0 1
4
1
y0 1
2
0
1/4
1/2
1
1
1
2
4
2
3
9
3
3
; x1 4 1 3; x2 9 4 5;
4
1
; y1 2 1 1; y2 3 2 1
2
b1 b0 1 3 1
b2 b1
4
c0
, c1
0,
2 x0 2 3 4
9
2 x1
b3 b2 1 15 1 3
2
c2
2 x2
2 5
75

17. Примеры

i
x
y
a
b
c
0
1/4
1/2
1/2
1
–4/9
1
1
1
1
1/3
0
2
3
4
9
2
3
2
3
1/3 1/15
–2/75
2
1
1 4
1
1
S0 x 1 x x , x ,1
2
4 9
4
4
1
2
S1 x 1 x 1 0 x 1 , x 1, 4
3
1
2
2
S 2 x 2 x 4 x 4 , x 4,9
3
75

18. Примеры

2
494
4 1 4 1 4 4 1
S0
0.678
729
9 2 9 4 9 9 4
1 9 17
9
S1 1 1
1.417
3 4 12
4
2
1 25
523
25
2 25
S2 2 4 4
2.615
3 4
200
4
75 4

19. Примеры

i
x
y
1
x0 1
4
1
y0 1
2
0
1/4
1/2
1
1
1
2
4
2
3
9
3
3
; x1 4 1 3; x2 9 4 5;
4
1
; y1 2 1 1; y2 3 2 1
2
2 y2
2 y1
1
2 1 1 7
b3 , b2
b3
, b1
b2
6
x2
5 6 30
x1
2 y0
2 1 7 13
2 1 2 13 9
, b0
b1
3 30 30
x0
3 4 30 10

20. Примеры

i
x
y
1
x0 1
4
1
y0 1
2
0
1/4
1/2
1
1
1
2
4
2
3
9
3
3
; x1 4 1 3; x2 9 4 5;
4
1
; y1 2 1 1; y2 3 2 1
2
b1 b0 13 30 9 10
b2 b1 7 39 13 30
14
c0
, c1
2 x0
2 3 4
45
2 x1
2 3
b3 b2 1 6 7 30
1
1
, c2
30
2 x2
2 5
150

21. Примеры

i
x
y
a
b
c
0
1
2
1/4
1
4
1/2
1
2
1/2
1
2
9/10 13/30 7/30
–14/45 –1/30 –1/150
3
9
3
3
1/6
2
1 9
1 14
1
1
S0 x x x , x ,1
2 10
4 45
4
4
13
1
2
S1 x 1 x 1 x 1 , x 1, 4
30
30
7
1
2
S2 x 2 x 4
x 4 , x 4,9
30
150

22. Примеры

2
967
4 1 9 4 1 14 4 1
S0
0.663
9 2 10 9 4 45 9 4 1458
2
13 9 1 9 143
9
S1 1 1 1
1.49
30 4 30 4
96
4
2
7 25
25
1 25
1993
2.491
2
2 4
4
30 4
800
4
150 4

23. Примеры

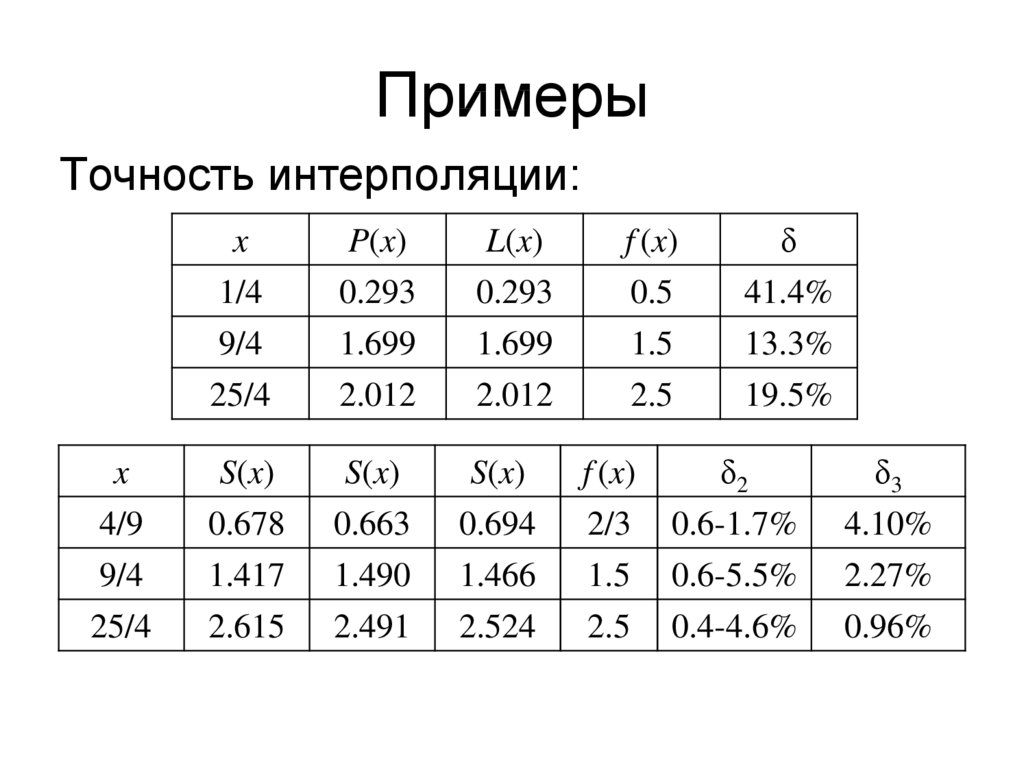
Точность интерполяции:
x
P(x)
L(x)
f (x)
δ
1/4
9/4
25/4
0.293
1.699
2.012
0.293
1.699
2.012
0.5
1.5
2.5
41.4%
13.3%
19.5%
x
4/9
S(x)
0.678
S(x)
0.663
f (x)
2/3
δ
0.6-1.7%
9/4
1.417
1.490
1.5
0.6-5.5%
25/4
2.615
2.491
2.5
0.4-4.6%

24. Примеры

Точность интерполяции:

25. Примеры

Кубический сплайн.
f x x
i
x
y
0
1/4
1/2
1
1
1
2
4
2
3
9
3
Результирующая сетка: {4/9, 9/4, 25/4}
1
1
B0 2, B3
Гранич. условия: f x
3
108
4 x
Далее строим сплайны S0(x), S1(x), S2(x).

26. Примеры

i
x
y
1
x0 1
4
1
y0 1
2
0
1/4
1/2
1
1
1
2
4
2
3
9
3
3
; x1 4 1 3; x2 9 4 5;
4
1
; y1 2 1 1; y2 3 2 1
2
1
5
1
1
1 3
3
x1
3 4 3
3 x0 x1
6
6
4
A
1
1
1
1
1
x1
x1 x2 3
3 5
6
3
6
3
2
1
2
8
3

27. Примеры

i
x
y
1
x0 1
4
1
y0 1
2
0
1/4
1/2
1
1
1
2
4
2
3
9
3
3
; x1 4 1 3; x2 9 4 5;
4
1
; y1 2 1 1; y2 3 2 1
2
y1 y0 x0
1 1 2 3 4
1
2
M
0
3 3 4 6
x x
0.0833
6
12
1
0
g
y2 y1 x2
1 1 5 1 407 0.1256
x x 6 M 3
3240
1
2
5 3 6 108

28. Примеры

5
4
1
2
1
2 M 1 0.0833
8 M 2 0.1256
3
1033
299
M1
0.0517; M 2
0.0374
19980
7992

29. Примеры

1033
299
1
M 0 2; M1
; M2
; M3
19980
7992
108
y0 x0
1 2 3 4
1033
b0
2 M 0 M 1 2 2
x0
6
34 6
19980
y1 x1
187513
1.1731; b1
2M1 M 2
159840
x1
6
1 3 1033 299 32267
2
0.4037; b2
3 6 19980 7992 79920
y2 x2
1 5 299 1 1349
0.2701
2M 2 M 3 2
x2
6
5 6 7992 108 4995

30. Примеры

1033
299
1
M 0 2; M1
; M2
; M3
19980
7992
108
1
1
c0 M 0 2 1;
2
2
1
1 1033
1033
c1 M 1
0.0259;
2
2 19980
39960
1
1 299
299
c2 M 2
0.0187
2
2 7992
15984

31. Примеры

1033
299
1
M 0 2; M1
; M2
; M3
19980
7992
108
1033
2
M1 M 0
38927
19980
d0
0.4330;
6 x0
6 3 4
89910
299 1033
M 2 M1
571
7992
19980
d1
0.0008;
6 x1
6 3
719280
1
299
M3 M2
5
108
7992
d2
0.0009
6 x2
6 5
5328

32. Примеры

i
x
y
a
b
c
d
0
1/4
1/2
1/2
1.1731
–1
0.4330
1
2
1
4
1
2
1
2
0.4037 0.2701
–0.0259 –0.0187
–0.0008 0.0009
2
3
9
3
3
2
1
1
1
1
1
S0 x 1.1731 x 1 x 0.4330 x , x ,1
2
4
4
4
4
S1 x 1 0.4037 x 1 0.0259 x 1 0.0008 x 1 , x 1, 4
2
3
S 2 x 2 0.2701 x 4 0.0187 x 4 0.0009 x 4 , x 4,9
2
3

33. Примеры

2
2
4 1
4 1
4 1
4 1
S0 1.1731 1 0.4330
9 2
9 4
9 4
9 4
0.6935
2
3
9
9
9
9
S1 1 0.2701 1 0.0259 1 0.0008 1
4
4
4
4
1.4658
2
3
25
25
25
25
S 2 2 0.3176 4 0.0187 4 0.0009 4
4
4
4
4
2.5236

34. Примеры

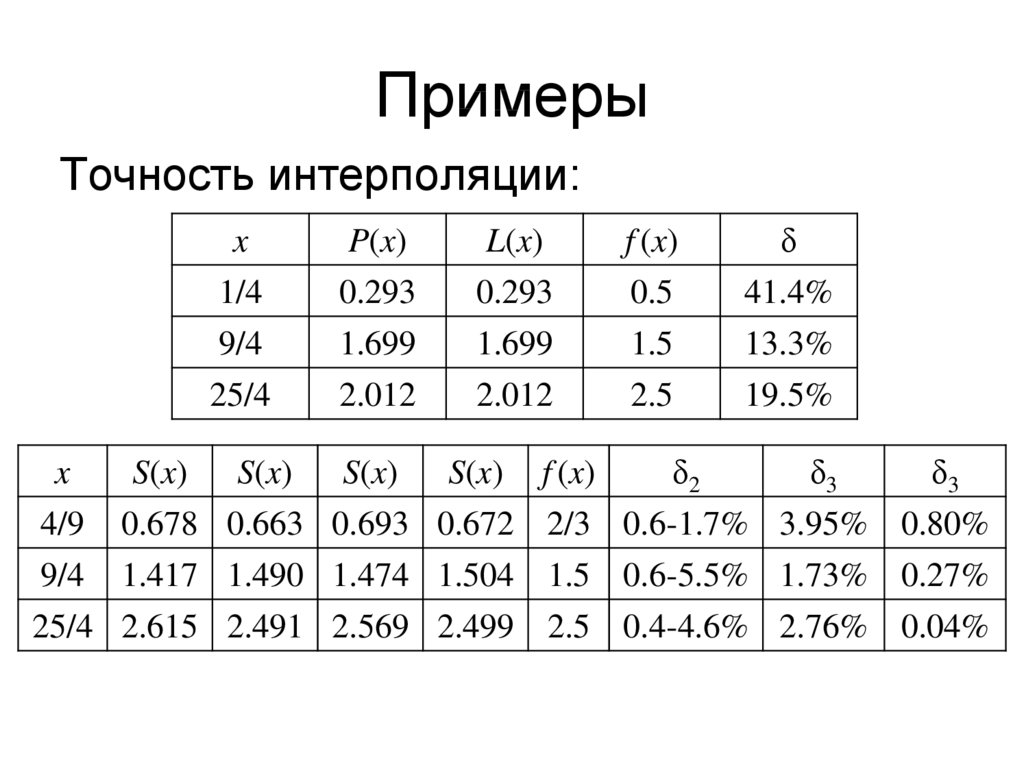
Точность интерполяции:
x
P(x)
L(x)
f (x)
δ
1/4
9/4
25/4
0.293
1.699
2.012
0.293
1.699
2.012
0.5
1.5
2.5
41.4%
13.3%
19.5%
x
4/9
S(x)
0.678
S(x)
0.663
S(x)
0.694
f (x)
2/3
δ2
0.6-1.7%
δ3
4.10%
9/4
1.417
1.490
1.466
1.5
0.6-5.5%
2.27%
25/4
2.615
2.491
2.524
2.5
0.4-4.6%
0.96%

35. Примеры

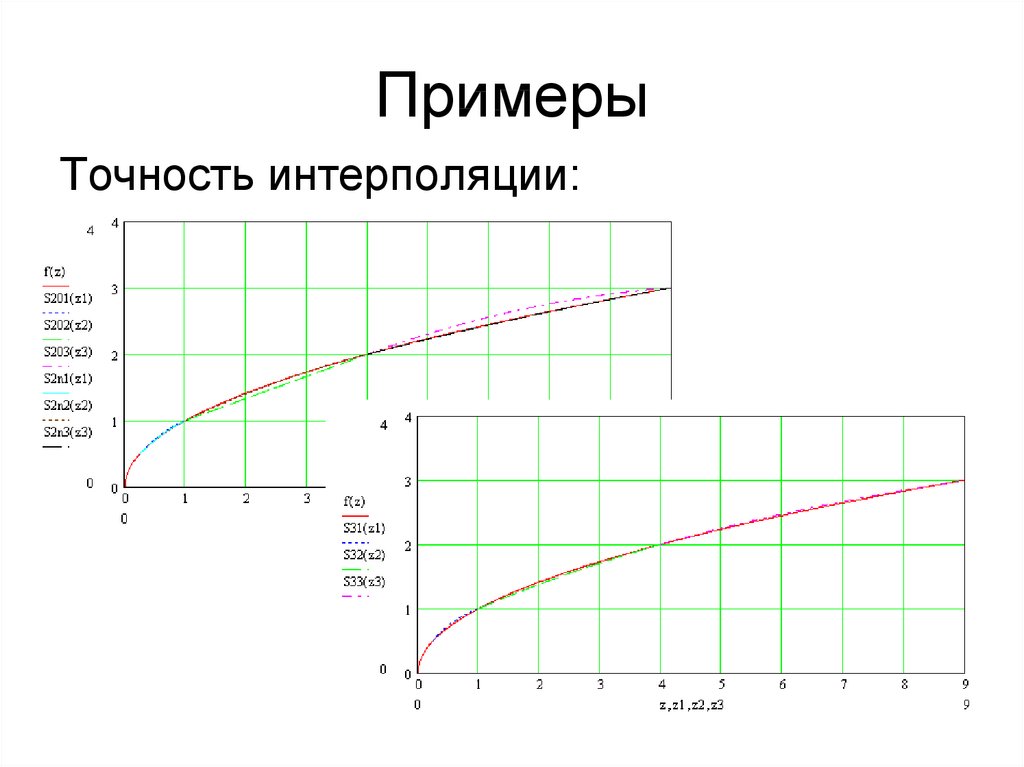
Точность интерполяции:

36. Примеры

Кубический сплайн.
f x x
i
x
y
0
1/4
1/2
1
1
1
2
4
2
3
9
3
Результирующая сетка: {4/9, 9/4, 25/4}
Гранич. условия:
1
1
f x
A0 1, A3
6
2 x
Далее строим сплайны S0(x), S1(x), S2(x).

37.

1
1
x0
0
3 x0
6
1
1 x 1 x x
x1
0
1
6 0 3
6
A
1
1
0
x1
x1 x2
6
3
1
0
0
x2
6
1 3
1 3
1
0
0
3 4
6 4
4
1
1
1 3 1 3 3
3
0
6 4 3 4
8
6
1
1
1
0
0
3
3
5
5
6
3
6
1
1
0
0
5
5 0
6
3
0
0
1
x2
6
1
x2
3
1
8
5
4
1
2
0
0
1
2
8
3
5
6
0
0
5
6
5
3

38. Примеры

y0
12
1
A
0
1
x
0
3
4
3
y1 y0 1 1 2
1
3
x1 x0
3
3
4
g
y2 y1 1 1
2
15
x
x
5
3
1
2
y2 1 1 1
A3
30
x2 6 5
2948
304
M0
1.2680; M 1
0.1308;
2325
2325
53
4
M2
0.0228; M 3
0.0086
2325
465

39. Примеры

2948
304
53
4
M0
; M1
;M2
; M3
2325
2325
2325
465
y1 x1
b0 A0 1; b1
2M 1 M 2
x1
6
1 3 304 53 737
2
0.4755; b2
3 6 2325 2325 1550
y2 x2
1 5 53 4
2M 2 M 3 2
x2
6
5 6 2325 465
38
0.2452
155

40. Примеры

2948
304
53
4
M0
; M1
;M2
; M3
2325
2325
2325
465
1
1 2948
1474
c0 M 0
0.6340;
2
2 2325
2325
1
1 304
152
c1 M 1
0.0654;
2
2 2325
2325
1
1 53
53
c2 M 2
0.0114
2
2 2325
4650

41. Примеры

2948
304
53
4
M0
; M1
;M2
; M3
2325
2325
2325
465
304 2948
M1 M 0
5288
2325
2325
d0
0.2527;
6 x0
6 3 4
20925
53
304
M 2 M1
251
2325
2325
d1
0.0060;
6 x1
6 3
41850
4
53
M3 M2
11
465
2325
d2
0.0005
6 x2
6 5
23250

42. Примеры

i
x
y
a
b
c
d
0
1
2
1/4
1
4
1/2
1
2
1/2
1
2
1
0.4755 0.2452
–0.6340 –0.0654 –0.0114
0.2527 0.0060 0.0005
2
3
9
3
3
2
1
1
1
1
1
S0 x 1 x 0.6340 x 0.2527 x , x ,1
2
4
4
4
4
S1 x 1 0.4755 x 1 0.0654 x 1 0.0040 x 1 , x 1, 4
2
3
S 2 x 2 0.2452 x 4 0.0114 x 4 0.0005 x 4 , x 4,9
2
3

43. Примеры

2
2
4 1
4 1
4 1
4 1
S0 1 0.6340 0.2527
9 2
9 4
9 4
9 4
0.6723
2
3
9
9
9
9
S1 1 0.4755 1 0.0654 1 0.0060 1
4
4
4
4
1.5039
2
3
25
25
25
25
S 2 2 0.2452 4 0.0114 4 0.0005 4
4
4
4
4
2.4993

44. Примеры

Точность интерполяции:
x
P(x)
L(x)
f (x)
δ
1/4
9/4
25/4
0.293
1.699
2.012
0.293
1.699
2.012
0.5
1.5
2.5
41.4%
13.3%
19.5%
x
4/9
S(x) S(x) S(x) S(x) f (x)
δ2
δ3
δ3
0.678 0.663 0.693 0.672 2/3 0.6-1.7% 3.95% 0.80%
9/4
1.417 1.490 1.474 1.504 1.5 0.6-5.5% 1.73% 0.27%
25/4 2.615 2.491 2.569 2.499 2.5 0.4-4.6% 2.76% 0.04%