Интерполяции сплайнами

1.

Интерполяции сплайнами
Интерполирование полиномом (n-1)-ой степени по совокупности по n
точкам часто бывает неудовлетворительным, особенно при больших
значениях n. В этих случаях полином степени n-1 может иметь n-2
локальный максимум и минимум и график может раскачиваться, чтобы
пройти через заданные точки, что часто бывает недопустимым.
В таких случаях часто применяют интерполяцию сплайнами.
Английское слово «spline» можно перевести как «гибкая линейка».

2.

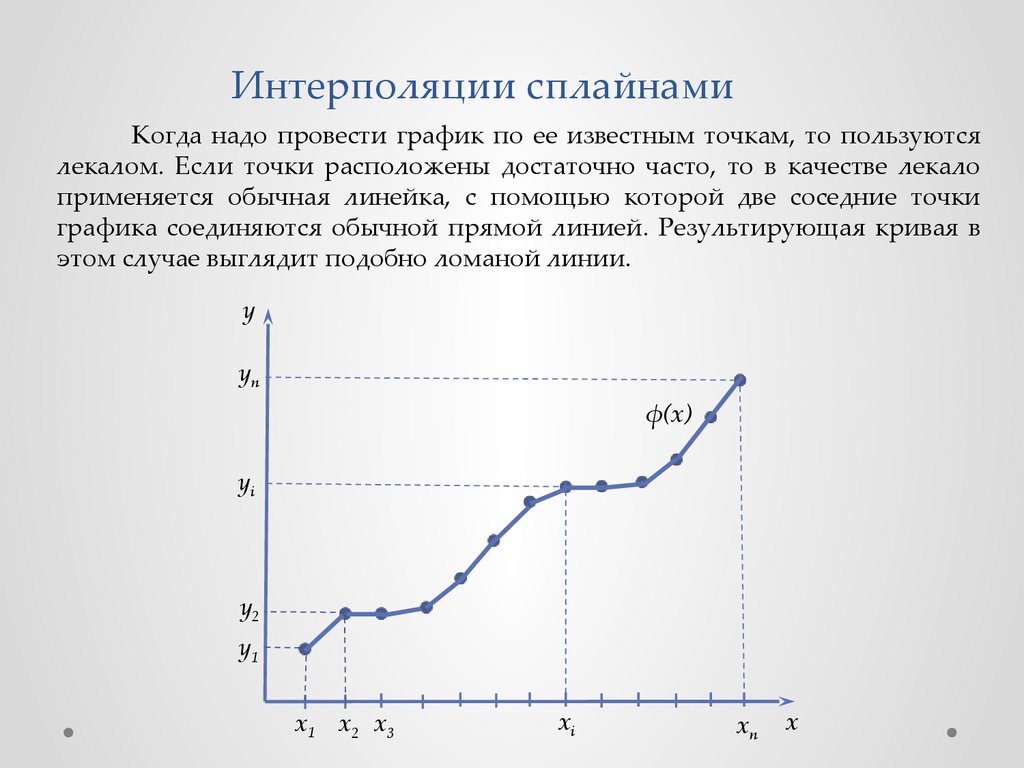
Интерполяции сплайнами
Когда надо провести график по ее известным точкам, то пользуются
лекалом. Если точки расположены достаточно часто, то в качестве лекало
применяется обычная линейка, с помощью которой две соседние точки
графика соединяются обычной прямой линией. Результирующая кривая в
этом случае выглядит подобно ломаной линии.
y
yn
φ(x)
yi
y2
y1
x1 x2 x3
xi
xn
x

3.

Интерполяции сплайнами
Эту ломаную линию называют линейным сплайном. Его можно записать
в виде формулы:
Si ( x) = yi + d i ( x - xi )
где
di = ( yi +1 - yi ) / ( xi +1 - xi )
(1)

4.

Интерполяции сплайнами
Совокупность таких прямых линий на всех n-1 отрезках будет
определять результирующую кривую ϕ(x) , представляющую собой
линейный сплайн :
ì y1 + d1 ( x - xдля
x в x x[ 1 , 2 ]
1)
ï
ï y2 + d 2 ( x - xдля
x в x x[ 2 , 3 ]
2)
ï
ï..........................................................
j ( x) = í
x в x x[ i , i +1 ]
ï yi + di ( x - xдля
i)
ï
ï...........................................................
ï y + d ( x - xдля) x в x x[ ,
n -1
n -1
n -1
î n -1
(2)
n
]

5.

Интерполяции сплайнами
Если точки расположены редко, то в качестве лекало можно применить
металлическую линейку, которую ставят на ребро и изгибают,
придерживая в нескольких местах пальцами так , чтобы ее ребро проходило
сразу через все точки графика. В этом случае кривая на отрезке между
двумя точками представляет собой полином 3-й степени.
Si ( x) = ai + bi ( x) + ci ( x) 2 + d i ( x)3
xi -1 £ x £ xi
(3)
совокупность таких полиномов на всех n-1 отрезках будет определять
результирующую кривую ϕ(x), представляющую собой кубический сплайн.
ì Sдля
x в x [x 1 , 2 ]
1
ï
ï Sдля
x в x [x 2 , 3 ]
2
ï
ï..........................................................
j ( x) = í
x в x [x i , i +1 ]
ï Sдля
i
ï
ï...........................................................
ï Sдля x в x [x , ]
n -1
n
î n -1
(4)

6.

Интерполяции сплайнами
Или в развернутом виде
ìa1 + b1 ( x) + c1 ( x) 2 + d1 ( xдля
)3
x в x x[ 1 , 2 ]
ï
ïa2 + b2 ( x) + c2 ( x) 2 + d 2 ( xдля
)3
x в x x[ 2 , 3 ]
ï
ï..........................................................
j ( x) = í
2
)3
x в x x[ i , i +1 ]
ïai + bi ( x) + ci ( x) + di ( xдля
ï
ï...........................................................
3
ïa + b ( x) + c ( x) 2 + d ( xдля
)
x в x [ xn -1 ,
n -1
n -1
î n -1 n -1
(5)
n
]

7.

Интерполяции сплайнами
Для построения кривой ϕ(x), необходимо определить неизвестные
коэффициенты
ai , bi , ci , d i
i = 1, 2,..., n - 1
общее число которых, как следует из формулы (8), составляет величину
4(n-1) значений. Следовательно необходимо составить систему состоящую
из 4(n-1) уравнений и ее решить.
В этой системе n уравнений определяют условие совпадения значений
сплайнов со значениями исходной функции
i = 1, 2,..., n - 1ü
ï
ý
S n -1 ( xn ) = yn
ï
þ
Si ( xi ) = yi
(6)

8.

Интерполяции сплайнами
Так как функция ϕ(x) должна быть непрерывной, то непрерывными
должны быть и все ее производные до второго порядка включительно.
Условие непрерывности записывается в виде
Непрерывность самой функции ϕ(x)
Si ( xi +1 ) = Si +1 ( xi +1 )
i = 1, 2,..., n - 2
(7)
Непрерывность первой производной функции ϕ(x)
Si' ( xi +1 ) = Si'+1 ( xi +1 )
i = 1, 2,..., n - 2
(8)
Непрерывность второй производной функции ϕ(x)
Si'' ( xi +1 ) = Si''+1 ( xi +1 )
i = 1, 2,..., n - 2
(9)

9.

Интерполяции сплайнами
Первая производная от S(x) вычисляется по формуле
Si' ( x ) = bi + 2ci x + 3di x 2
i = 1, 2,..., n - 2
Вторая производная определяется формулой
Si'' ( x ) = 2ci + 6di x
i = 1, 2,..., n - 2

10.

Интерполяции сплайнами
Мы получили n +3(n-2) = 4n-6 уравнений из необходимых 4(n-1).
Недостающие два уравнения обычно определяют, исходя из тех или иных
граничных условий. Предположим, что функция ϕ(x) на своих границах
удовлетворяет условиям
j '' ( x1 ) = j '' ( xn ) = 0
тогда имеем следующую недостающую пару значений
j '' ( x1 ) = S1'' ( x1 ) = 0
j '' ( xn ) = S n'' -1 ( xn ) = 0

11.

Интерполяции сплайнами
Или в развернутом виде
j '' ( x1 ) = S1'' ( x1 ) = ( a1 + b1 ( x1 ) + c1 ( x1 ) 2 + d1 ( x1 )3 ) '' = 0
j '' ( xn ) = Sn'' -1 ( xn ) = ( an -1 + bn -1 ( xn ) + cn -1 ( xn ) 2 + d n -1 ( xn )3 ) '' = 0
Вычисляя производные первого и второго порядка получим
j '' ( x1 ) = S1'' ( x1 ) = 2c1 = 0
j '' ( xn ) = S n'' -1 ( xn ) = 2cn -1 ( xn ) + 6d n -1 ( xn ) = 0
или
c1 = 0
ü
ý
cn -1 ( xn ) + 3d n -1 ( xn ) = 0 þ
(10)

12.

Интерполяции сплайнами
Таким образом мы получили все 4(n-1) уравнений, которых достаточно
для определения всех коэффициентов
ai , bi , ci , d i
i = 1, 2,..., n - 1
Уравнения 9 ÷ 13 однозначно определяют кубический сплайн ϕ(x).

13.

Пример 2.
Из эксперимента получены такие значения функции f(x):
x
х1 = 0
х2 = 1
х3 = 2
х4 = 3
х5 = 4
f(x)
y1 = 1
y2 = 1.8
y3 = 2.2
y4 = 1.4
y5 = 1
Требуется представить приближенно функцию у = f(х) линейным и
кубическим сплайном. В данном случае n=5.

14.

Интерполяция линейным сплайном

15.

Для аппроксимации данной табличной функции линейным сплайном
используем формулу (1). Определим сначала значения di, число которых
составит величину n-1=4
0.8
1
0.4
d 2 = ( y3 - y2 ) / ( x3 - x2 ) = (2.2 - 1.8) / (2 - 1) =
1
-0.8
d3 = ( y4 - y3 ) / ( x4 - x3 ) = (1.4 - 2.2) / (3 - 2) =
1
-0.4
d 4 = ( y5 - y4 ) / ( x5 - x4 ) = (1 - 1.4) / (4 - 3) =
1
d1 = ( y2 - y1 ) / ( x2 - x1 ) = (1.8 - 1) / (1 - 0) =

16.

Подставляем значения di, в формулу (2)
0.8
ì
S
(
x
)
=
y
+
d
(
x
x
)
=
1
+
( x - 0) = 1 + 0.8 xдля x в
1
1
1
ï 1
1
ï
ï S ( x) = y + d ( x - x ) = 1.8 + 0.4 ( x - 1) = 1.4 + 0.4 xдля x
2
2
2
ï 2
1
j ( x) = í
ï S ( x ) = y + d ( x - x ) = 2.2 + -0.8 ( x - 2) = 3.8 + 0.8 xдля
3
3
3
ï 3
1
ï
-0.4
ï S 4 ( x) = y4 + d 4 ( x - x4 ) = 1.4 +
( x - 3) = 2.6 - 0.4 xдля
î
1
Построим график этой функции…
x[
1
в
= x0,
2
x[
=x1,
2
= 1]
3
= 2]
x в
x[
3
= x2,
4
= 3]
x в
x[
4
= x3,
5
= 4]

17.

График линейного сплайна.
2.5
2
1.5
1
­1
0
1
2
3
4
5

18.

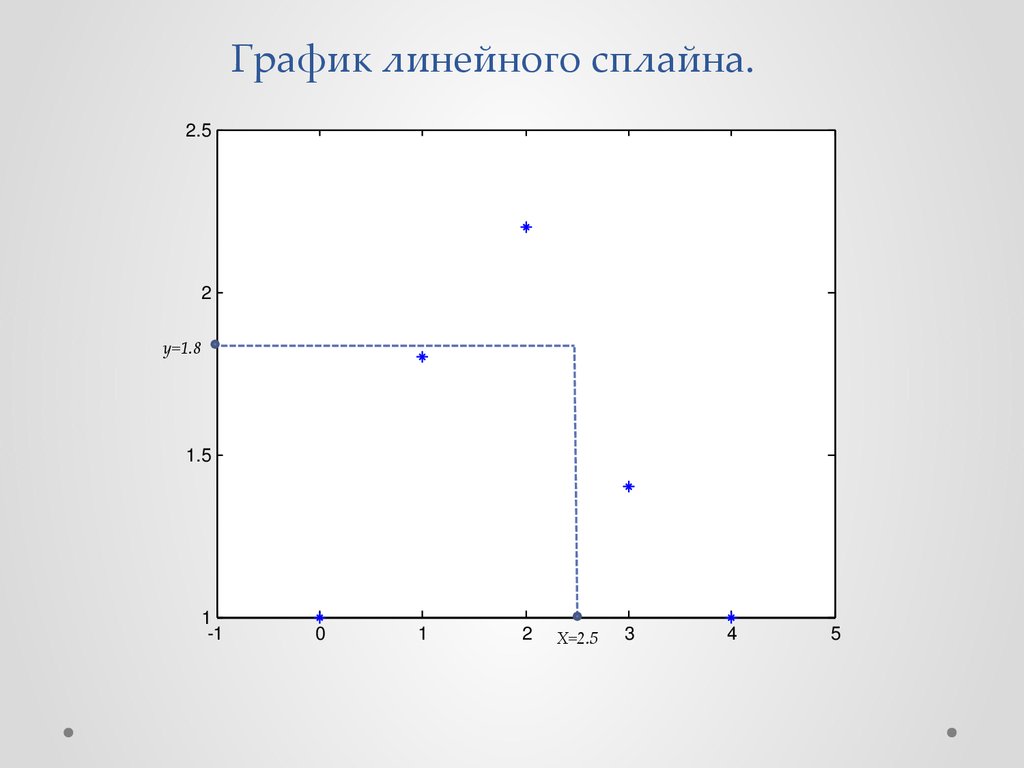
Определим значение функции ϕ(x) при x=2.5. Для этого расчета
принимаем сплайн номер три, для отрезка х=2÷3.
S3 ( x) = 3.8 - 0.8 xдля
x в
x[
3
= x2,
Подставляем x=2.5 и получаем
S3 ( x) = 3.8 - 0.8 * 2.5 = 3.8 - 2 = 1.8
4
= 3]

19.

График линейного сплайна.
2.5
2
y=1.8
1.5
1
­1
0
1
2
X=2.5
3
4
5

20.

Интерполяция кубическим сплайном

21.

Для интерполяции кубическим сплайном требуется составить систему,
состоящую
из
4(n-1)=4(5-1)=16
уравнений
с
16
неизвестными
коэффициентами

22.

В матричной форме эта система будет выглядеть следующим образом
W*X =Z
где W – квадратная матрица, состоящая из коэффициентов при
неизвестных параметрах системы, в нашем случае имет
размер 16 х 16;
X– вектор неизвестных параметров системы, в нашем случае
состоит из 16 значений неизвестных
ai , bi , ci , d i
i = 1, 2,..., n - 1
Z – вектор правых частей уравнений ситемы, состоит также из
16 значений.

23.

Неизвестные параметры системы будут определятся как
Z
X =
W
Для вычислений сначала составим матрицу W и вектор Z.
Для этого заполним строки следующей таблицы…

24.

Таблица коэффициентов при неизвестных параметрах системы
и значений правых частей системы.
a1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
1
2
3
4
5
6
7
8
9
10
11
12
Область, определяющая матрицу коэффициентов
при неизвестных W
d4

25.

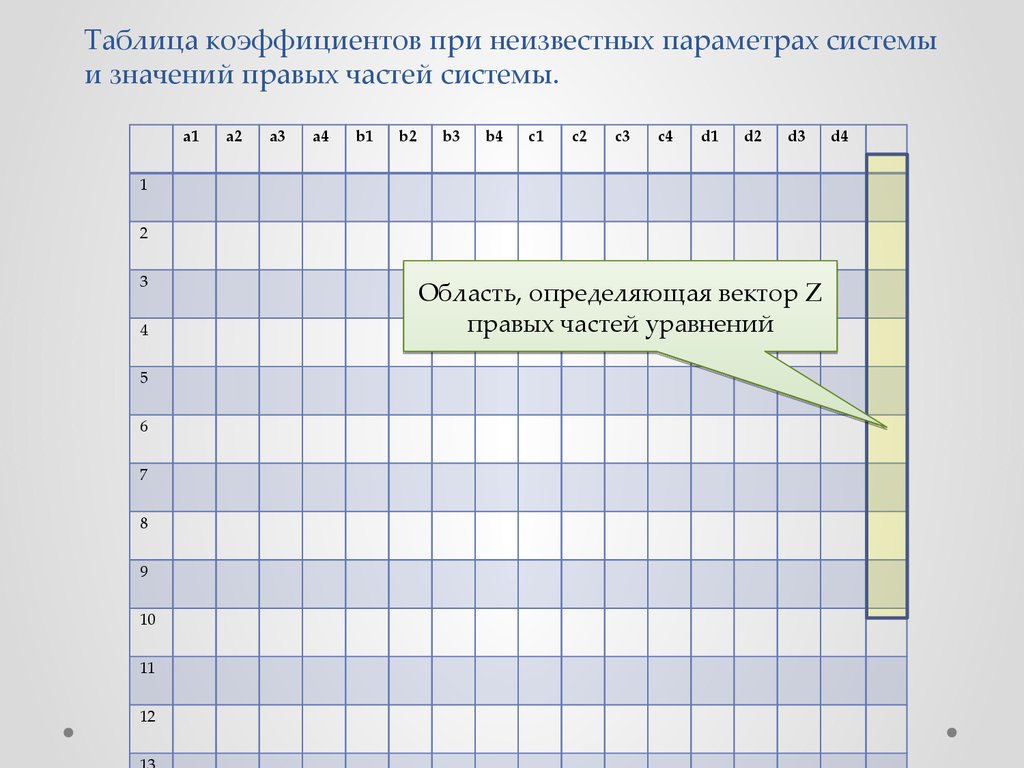
Таблица коэффициентов при неизвестных параметрах системы
и значений правых частей системы.
a1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
1
2
3
4
5
6
7
8
9
10
11
12
Область, определяющая вектор Z
правых частей уравнений
d4

26.

Система уравнений для интерполяции кубическим сплайном,
состоящая
из
4(n-1)=4(5-1)=16
уравнений
с
12
неизвестными
коэффициентами составляется поэтапно

27.

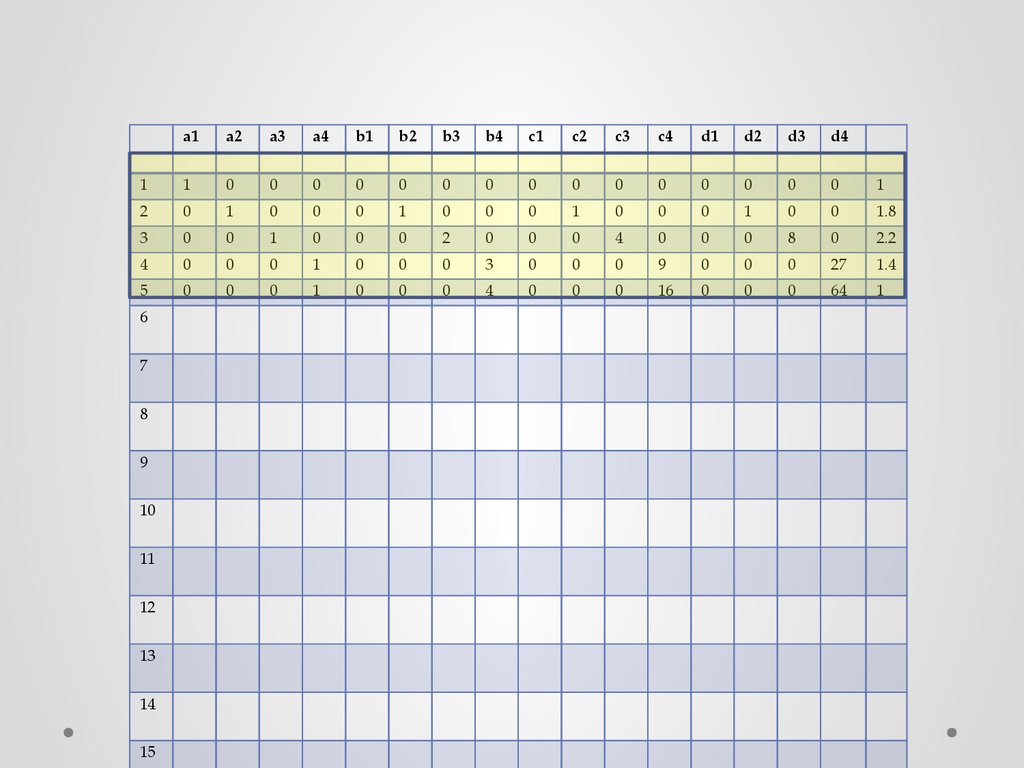
Сначала составим 5 уравнений согласно формуле (5)
S1 ( x1 ) = S1 (0) = a1 + b1 0 + c1 0 + d1 0 = 1.0
ü
ï
S 2 ( x2 ) = S 2 (1) = a2 + b21 + c21 + d 21 = 1.8
ï
ï
S3 ( x3 ) = S3 (2) = a3 + b3 2 + c3 4 + d 3 8 = 2.2 ý
S 4 ( x4 ) = S 4 (3) = a4 + b4 3 + c4 9 + d 4 27 = 1.4 ï
ï
S 4 ( x5 ) = S 4 (4) = a4 + b4 4 + c416 + d 4 64 = 1.0 ï
þ
На основании этих уравнений заполняются первые пять строк
матрицы…

28.

a1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
d4
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
1.8
3
0
0
1
0
0
0
2
0
0
0
4
0
0
0
8
0
2.2
4
0
0
0
1
0
0
0
3
0
0
0
9
0
0
0
27
1.4
5
0
0
0
1
0
0
0
4
0
0
0
16
0
0
0
64
1
6
7
8
9
10
11
12
13
14
15

29.

Составим еще n-2=5-2 =3 уравнений согласно формуле (7), которые
обеспечивают соблюдение условия непрерывности функции
S1 ( x2 ) = S 2 ( x2 )
S 2 ( x3 ) = S3 ( x3 )
S3 ( x4 ) = S 4 ( x4 )
S1 (1) = S 2 (1) ü
ï
ï
S 2 (2) = S3 (2) ý
ï
S3 (3) = S 4 (3) ï
þ
Составляя уравнения и производя определенные преобразования,
получаем
a1 - a2 + b1 - b2 + c1 - c2 + d1 - d 2 = 0
ü
ï
a2 - a3 + 2b2 - 2b3 + 4c2 - 4c3 + 8d 2 - 8d 3 = 0 ý
a3 - a4 + 3b3 - 3b4 + 9c3 - 9c4 + 27d 3 - 27d 4 = 0 ï
þ
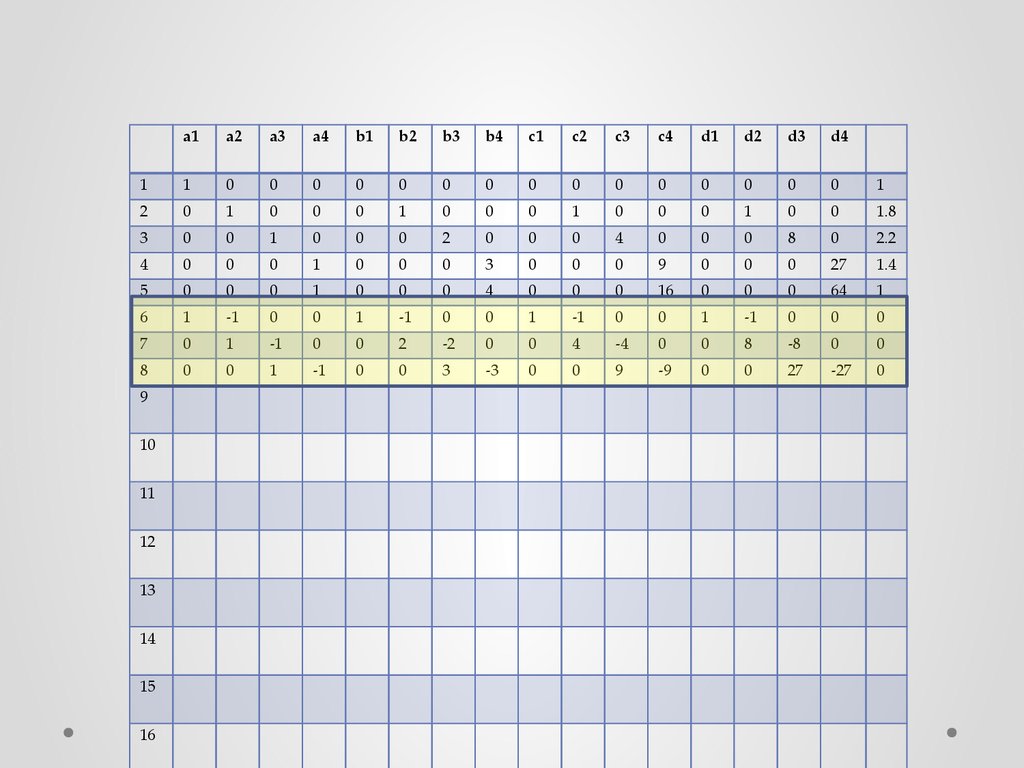
На основании этих уравнений заполняются 6, 7 и 8 строки матрицы…

30.

a1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
d4
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
1.8
3
0
0
1
0
0
0
2
0
0
0
4
0
0
0
8
0
2.2
4
0
0
0
1
0
0
0
3
0
0
0
9
0
0
0
27
1.4
5
0
0
0
1
0
0
0
4
0
0
0
16
0
0
0
64
1
6
1
-1
0
0
1
-1
0
0
1
-1
0
0
1
-1
0
0
0
7
0
1
-1
0
0
2
-2
0
0
4
-4
0
0
8
-8
0
0
8
0
0
1
-1
0
0
3
-3
0
0
9
-9
0
0
27
-27
0
9
10
11
12
13
14
15
16

31.

Составим еще n-2=5-2 =3 уравнений согласно формуле (8), которые
обеспечивают соблюдение условия непрерывности 1-й производной
функции
S1' ( x2 ) = S 2' ( x2 )
S 2' ( x3 ) = S3' ( x3 )
S3' ( x4 ) = S 4' ( x4 )
S1' (1) = S 2' (1) ü
ï
ï
'
'
S 2 (2) = S3 (2) ý
ï
'
'
S3 (3) = S 4 (3) ï
þ
Также составляя уравнения и производя над ними определенные
преобразования, получаем
b1 - b2 + 2c1 - 2c2 + 3d1 - 3d 2 = 0
ü
ï
b2 - b3 + 4c2 - 4c3 + 12d 2 - 12d 3 = 0 ý
b3 - b4 + 6c3 - 6c4 + 27d 3 - 27 d 4 = 0 ï
þ
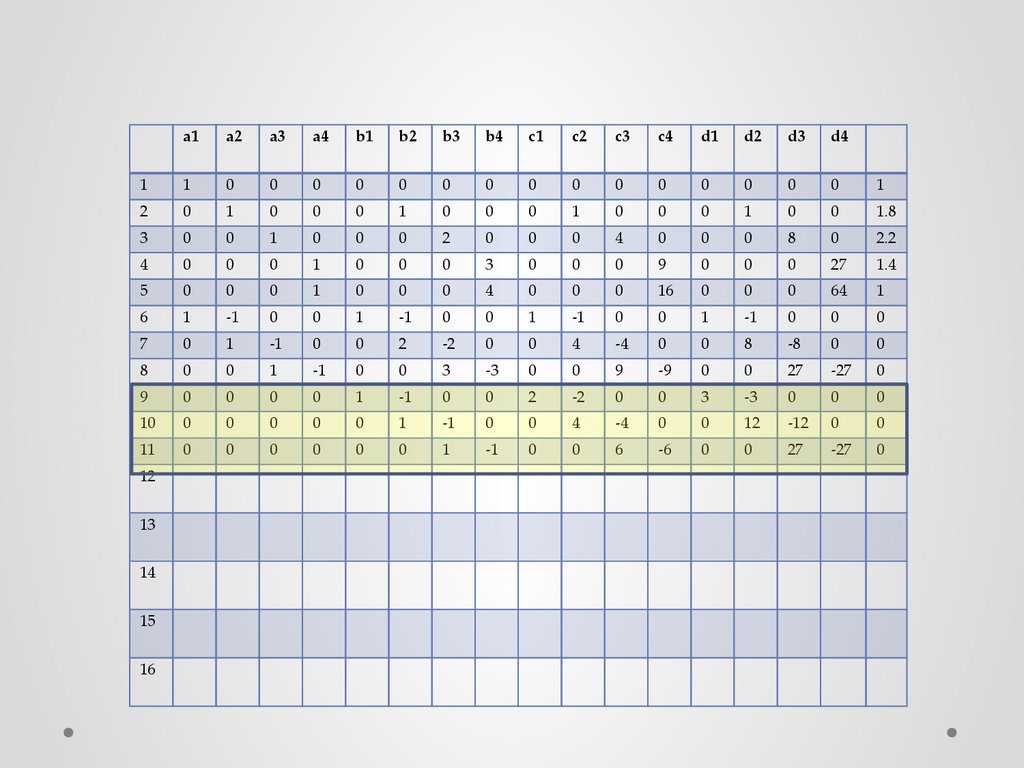
На основании этих уравнений заполняются 9, 10 и 11 строки матрицы…

32.

a1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
d4
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
1.8
3
0
0
1
0
0
0
2
0
0
0
4
0
0
0
8
0
2.2
4
0
0
0
1
0
0
0
3
0
0
0
9
0
0
0
27
1.4
5
0
0
0
1
0
0
0
4
0
0
0
16
0
0
0
64
1
6
1
-1
0
0
1
-1
0
0
1
-1
0
0
1
-1
0
0
0
7
0
1
-1
0
0
2
-2
0
0
4
-4
0
0
8
-8
0
0
8
0
0
1
-1
0
0
3
-3
0
0
9
-9
0
0
27
-27
0
9
0
0
0
0
1
-1
0
0
2
-2
0
0
3
-3
0
0
0
10
0
0
0
0
0
1
-1
0
0
4
-4
0
0
12
-12
0
0
11
0
0
0
0
0
0
1
-1
0
0
6
-6
0
0
27
-27
0
12
13
14
15
16

33.

Составим еще n-2=5-2 =3 уравнений согласно формуле (9), которые
обеспечивают соблюдение условия непрерывности 2-й производной
функции
S1'' ( x2 ) = S 2'' ( x2 )
S 2'' ( x3 ) = S3'' ( x3 )
S3'' ( x4 ) = S 4'' ( x4 )
S1'' (1) = S 2'' (1) ü
ï
ï
''
''
S 2 (2) = S3 (2) ý
ï
''
''
S3 (3) = S 4 (3) ï
þ
Также составляя уравнения и производя над ними определенные
преобразования, получаем
2c1 - 2c2 + 6d1 - 6d 2 = 0
ü
ï
2c2 - 2c3 + 12d 2 - 12d3 = 0 ý
2c3 - 2c4 + 18d 3 - 18d 4 = 0 ï
þ
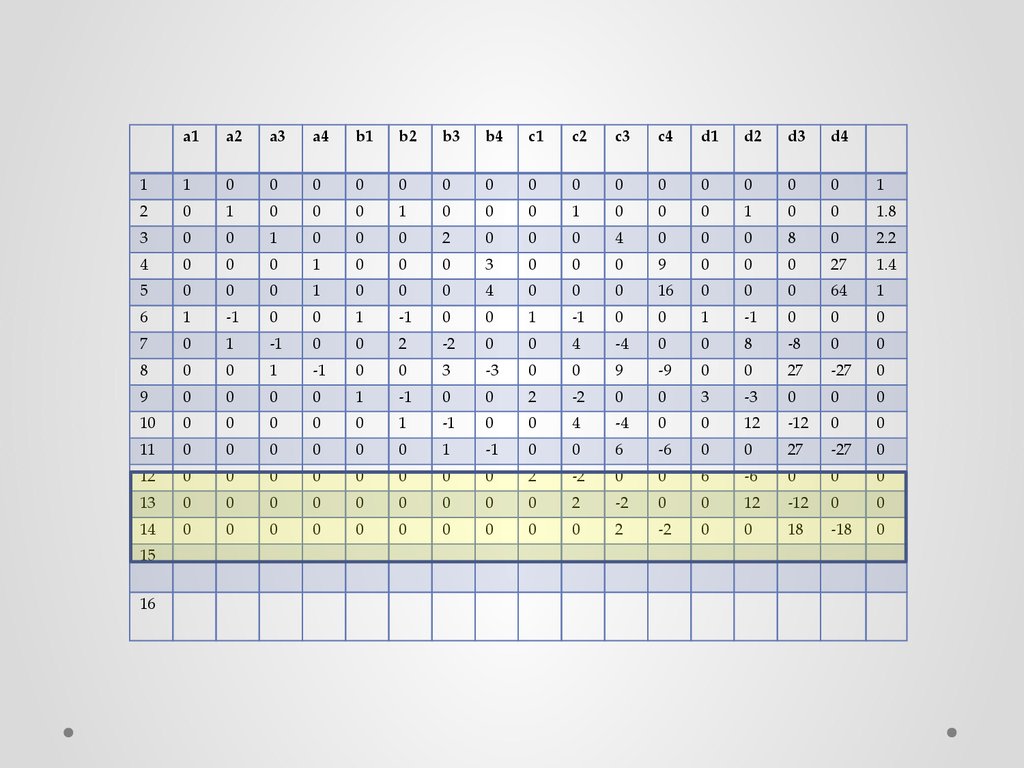
На основании этих уравнений заполняются 12, 13 и 14 строки
матрицы…

34.

a1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
d4
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
1.8
3
0
0
1
0
0
0
2
0
0
0
4
0
0
0
8
0
2.2
4
0
0
0
1
0
0
0
3
0
0
0
9
0
0
0
27
1.4
5
0
0
0
1
0
0
0
4
0
0
0
16
0
0
0
64
1
6
1
-1
0
0
1
-1
0
0
1
-1
0
0
1
-1
0
0
0
7
0
1
-1
0
0
2
-2
0
0
4
-4
0
0
8
-8
0
0
8
0
0
1
-1
0
0
3
-3
0
0
9
-9
0
0
27
-27
0
9
0
0
0
0
1
-1
0
0
2
-2
0
0
3
-3
0
0
0
10
0
0
0
0
0
1
-1
0
0
4
-4
0
0
12
-12
0
0
11
0
0
0
0
0
0
1
-1
0
0
6
-6
0
0
27
-27
0
12
0
0
0
0
0
0
0
0
2
-2
0
0
6
-6
0
0
0
13
0
0
0
0
0
0
0
0
0
2
-2
0
0
12
-12
0
0
14
0
0
0
0
0
0
0
0
0
0
2
-2
0
0
18
-18
0
15
16

35.

Составляем последние 2 уравнения по формуле (10), которые
обеспечивают соблюдение условия нулевой кривизны функции на ее
концах в точках 1 и n , что соответствует отпущенным концам линейки
c1 = 0
ü
ý
c4 + 12d 4 = 0 þ
На основании этих уравнений заполняются последние 15 и 16 строки
матрицы…

36.

a1
a2
a3
a4
b1
b2
b3
b4
c1
c2
c3
c4
d1
d2
d3
d4
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
1.8
3
0
0
1
0
0
0
2
0
0
0
4
0
0
0
8
0
2.2
4
0
0
0
1
0
0
0
3
0
0
0
9
0
0
0
27
1.4
5
0
0
0
1
0
0
0
4
0
0
0
16
0
0
0
64
1
6
1
-1
0
0
1
-1
0
0
1
-1
0
0
1
-1
0
0
0
7
0
1
-1
0
0
2
-2
0
0
4
-4
0
0
8
-8
0
0
8
0
0
1
-1
0
0
3
-3
0
0
9
-9
0
0
27
-27
0
9
0
0
0
0
1
-1
0
0
2
-2
0
0
3
-3
0
0
0
10
0
0
0
0
0
1
-1
0
0
4
-4
0
0
12
-12
0
0
11
0
0
0
0
0
0
1
-1
0
0
6
-6
0
0
27
-27
0
12
0
0
0
0
0
0
0
0
2
-2
0
0
6
-6
0
0
0
13
0
0
0
0
0
0
0
0
0
2
-2
0
0
12
-12
0
0
14
0
0
0
0
0
0
0
0
0
0
2
-2
0
0
18
-18
0
15
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
16
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
12
0

37.

Решаем эту систему уравнений любым из известных способов и
получаем следующие неизвестные коэффициенты
b1 = 0.8143
c1 = 0
d1 = -0.0143
b2 = -0.1286
c2 = 0.9429
d 2 = -0.3286
a3 = -5.5429
b3 = 10.1571
c3 = -4.2
d3 = 0.5286
a4 = 13.7429
b4 = -9.1286
c4 = 2.2286
d 4 = -0.1857
a1 = 1
a2 = 1.3143

38.

В итоге формула (5) принимает вид
ì1 + 0.8143( x) - 0.0143( xдля
)3
x в x [ 1=
x 0, 2 = 1]
ï
ïï1.3143 - 0.1286( x) + 0.9429( x) 2 - 0.3286( xдля
)3
x в x [ 2 x= 1, 3 = 2]
j ( x) = í
2
)3
x в x [ 3=
x 2, 4 = 3]
ï-5.5429 + 10.1571( x) - 4.2( x) + 0.5286( xдля
ï
2
)3
x в x [ 4 = 3, x5 = 4]
ïî13.7429 - 9.1286( x) + 2.2286( x) - 0.1857( xдля
Построим график этой функции…

39.

График кубического сплайна.
3.5
3
2.5
2
1.5
1
0.5
­1
0
1
2
3
4
5

40.

Определим значение функции ϕ(x) при x=2.5. Для этого расчета
принимаем сплайн номер три, для отрезка х=2÷3.
S3 ( x ) = -5.5429 + 10.1571( x) - 4.2( x) 2 + 0.5286( xдля
)3
x в
x [
3
=
x 2,
Подставляем x=2.5 и получаем
S3 ( x ) = -5.5429 + 10.1571(2.5) - 4.2(2.5) 2 + 0.5286(2.5) 3 = 1.859
4
= 3]

41.

График кубического сплайна.
3.5
3
2.5
2
y=1.859
1.5
1
0.5
­1
0
1
2
X=2.5
3
4
5

42.

График линейного и кубического сплайна.
2.6
2.4
2.2
2
1.8
1.6
1.4
1.2
1
0.8
­1
­0.5
0
0.5
1
1.5
2
2.5
3
3.5
4