Дискретне перетворення Фур’є. Лекція 2

1. ЦОС Лекція 2

2.

Що чує вухо?

3.

4. Тема лекції

Дискретне перетворення Фур’є
перехід в частотну область
«Будь-яка достатньо розвинена технологія нічим не
відрізняється від магії» Артур С.Кларк

5. Важливо пам’ятати Пряме перетворення Фур’є здійснює перехід з часової області сигналу в частотну (в результаті перетворення ми

знаємо які частоти є в сигналі)
Зворотнє перетворення Фур’є здійснює перехід з
частотної області сигналу в часову

6. Дискретне перетворення Фур’є використовується для дискретизованого сигналу

(вхідний сигнал)
x(nT ) x(0), x(T )...x(( N 1)T )
N – кількість відліків, які слідують в часі з періодом
fd 1
дискретизації Т= t, та частотою дискретизації
T
- частота першої гармоніки
{ X (k )} X (0), X ( ),... X (( N 1) )
2
2 2 f d
( N 1)T NT
N
N>>1

7. Формули розрахунку ДПФ

N 1
X (k ) x(nT )e ik nT
Враховуючи що
n 0
N 1
2
NТ
X ( к ) x ( n )e
n 0
i
k 2 n
N

8. Приклад ДПФ для послідовності чотирьох чисел

1,0,0,1
N=4
x(0) 1
f d 8000 Гц
x(1T ) 0
x(2T ) 0
1
T
125 мкс
8000
Знайти X(0) X(1) X(2) X(3)
x(3T ) 1

9. Приклад ДПФ для послідовності чотирьох чисел

1,0,0,1
x(0) 1
f d 8000 Гц
N=4
x(2T ) 0
x(1T ) 0
1
T
125 мкс
8000
Знайти X(0) X(1) X(2) X(3)
3
X (0) x(nT )e i 0 1 0 0 1 2
n 0
x(3T ) 1

10. Приклад ДПФ для послідовності чотирьох чисел

1,0,0,1
x(0) 1
f d 8000 Гц
N=4
x(2T ) 0
x(1T ) 0
1
T
125 мкс
8000
x(3T ) 1
Знайти X(0) X(1) X(2) X(3)
3
X (0) x(nT )e i 0 1 0 0 1 2
n 0
3
X (1) x(nT )e
n 0
X (2) 0
X (3) 1 i
i
1 2 n
N
1e
i
2 0
4
0 0 1 e
i
2 3
4
1 cos(
3
3
) i sin( ) 1 i
2
2

11. Важливі узагальнення

В результаті ДПФ над N числами отримуємо комплексний вектор
чисел довжиною N.
Частина результуючого вектора до N/2 є комплексно спряженою
до другої половини.
В ЦОС достатньо розглядати лише першу половину
результуючого вектора, оскільки вона відповідає за частотний
діапазон сигналу від 0 до fd/2 fmax. Далі по частотній шкалі
відбувається віддзеркалення спектру.
Графічна залежність Х від частоти (кратної до частоти
дискретизації) отримала назву спектру сигналу.

12. Результат чисельний та графічний

Чисельний результат
X 2,1 i,0,1 i
Графічний
2
m=0..N/2
X
На графіку m=0..N
2
1
fd
m
N

13. Зворотнє (обернене) перетворення Фур’є

N 1
1
ik nT
х(nT ) X (k )e
N k 0

14. Обчислювальна складність ДПФ

Наприклад для 8 точок
7
X (k ) x(n)e i 2 kn/8
n 0
Кількість точок 8
Кількість точок N
Кількість точок 1024
8 множення
N множення
1024 множення
7 додавання
N-1 додавання
1023 додавання
8*8+8*7=120
N*N+N*(N-1)
1024*1024+1024*1023= 106
Висновок: через високу обчислювальну складність використовують
алгоритми швидкого перетворення Фур’є

15. FFT fft ШПФ БПФ алгоритм Кулі-Тьюкі (Cooley-Tukey)

Знижує об’єм обчислень
Використовує децимацію (проріджування) в часовій області
Використовується для послідовностей довжиною 2n
N 1
X ( k ) x ( n )e
n 0
Де позначено
Легко довести
WN e
ik 2 n / N
N 1
x(n)WNkn
n 0
2
N
W e
2
N
i
2 2
N
e
i
2
N /2
WN /2

16. Основна ідея Вхідну послідовність розбиваємо на дві: парну і непарну Результатом є сума Фур’є перетворень для половини

послідовності
з ваговим коефіцієнтом W
Доведемо за допомогою формули ДПФ
N 1
X (k ) x(n)WNnk
N 1
2
n 0
N 1
2
n 0
n 0
N 1
2
x(2n)WN2 nk x(2n 1)WN(2 n 1) k
n 0
x(2n)WNnk/2 WNk
X 11 парної
N 1
2
n 0
x(2n 1)WNnk/2
X 12 непарної

17. Приклад «знайомої» послідовності {1,0,0,1} чотирьохточкове перетворення FFT

ДОПОМІЖНІ ОБЧИСЛЕННЯ W
x(0) x(1) x(2) x(3)
Розбиваємо на 2 по 2
x(0) x(2)
x(1) x(3)
X 21 (0) x(0) x(2) 1
X 22 (0) x(1) x(3) 1
X 21 (1) x(0) x(2) 1
X 22 (1) x(1) x(3) 1
W e
1
2
X (0) X 21 (0) W X 22 (0) 2
0
4
X (3) X 21 (1) W43 X 22 (1) 1 i
i
2
1
2
1 W e
1
4
i
W e
Отримали такий
самий результат як і
при ДПФ
2
4
i
i
2
2
4
i
2
3
4
W e
2
4
3
4
X (1) X 21 (1) W41 X 22 (1) 1 i
X (2) X 21 (0) W42 X 22 (0) 0
W40 1
W20 1
1
i

18. Схема метелика

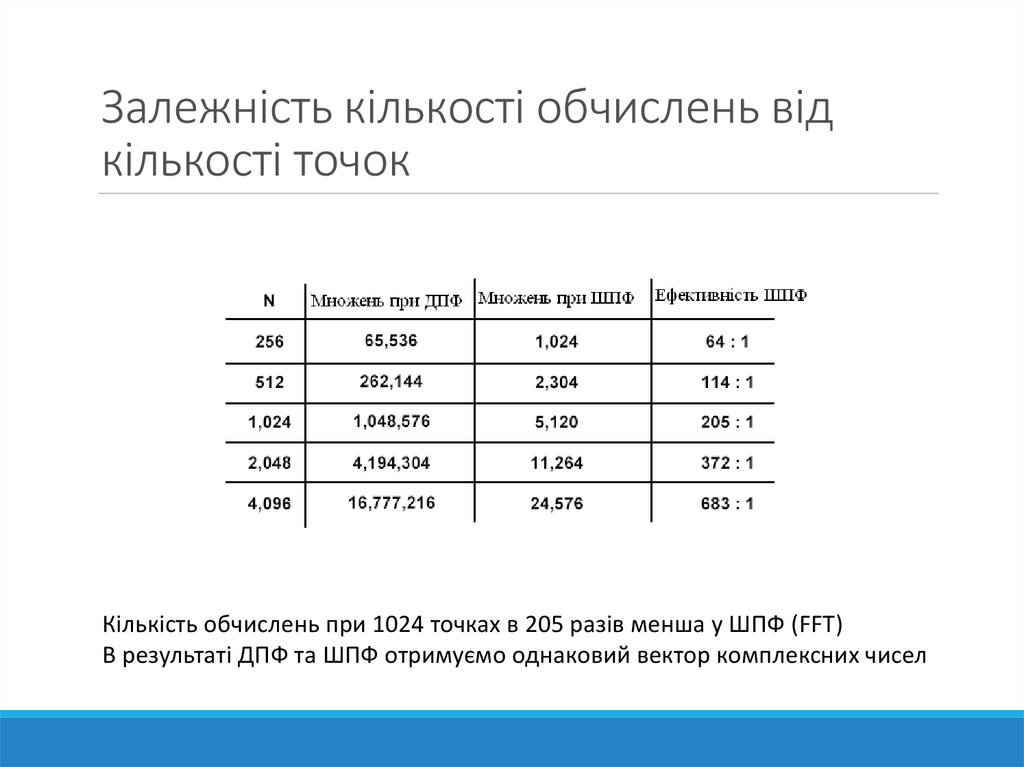
19. Залежність кількості обчислень від кількості точок

Кількість обчислень при 1024 точках в 205 разів менша у ШПФ (FFT)
В результаті ДПФ та ШПФ отримуємо однаковий вектор комплексних чисел

20.

21.

22. У зв’язку з широким використанням FFT в усіх мовах програмування є бібліотеки, які його реалізують

23.

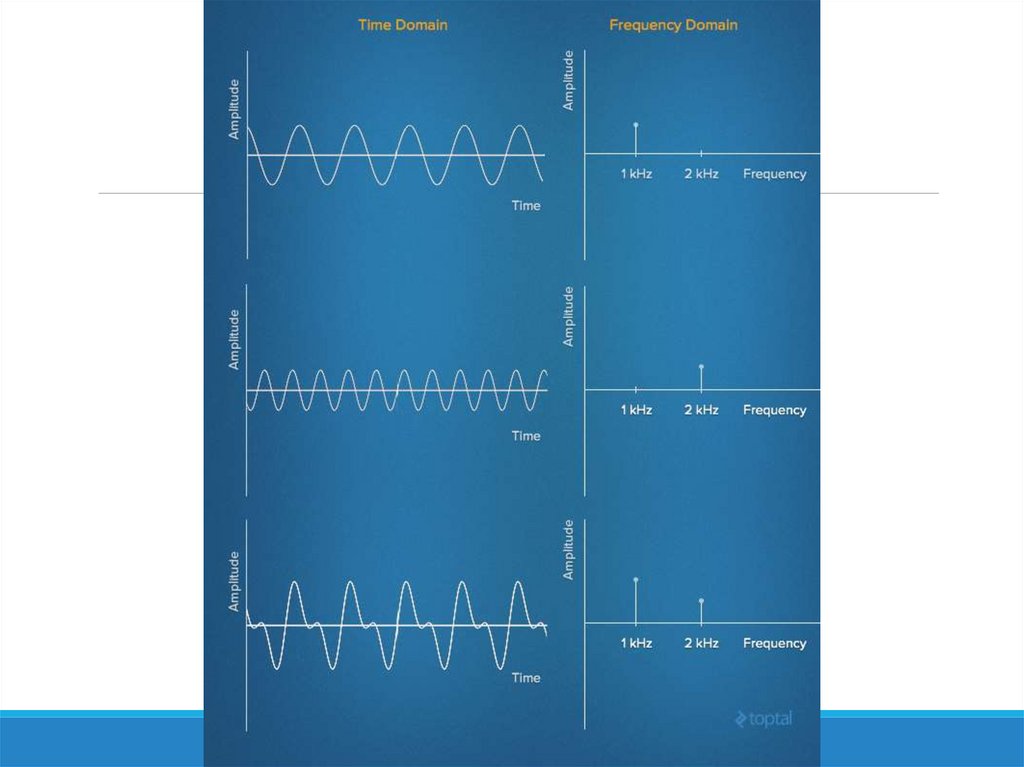
Приклади сигналів та їх спектрів
* Гармонічний
* Прямокутні імпульси
* Шум
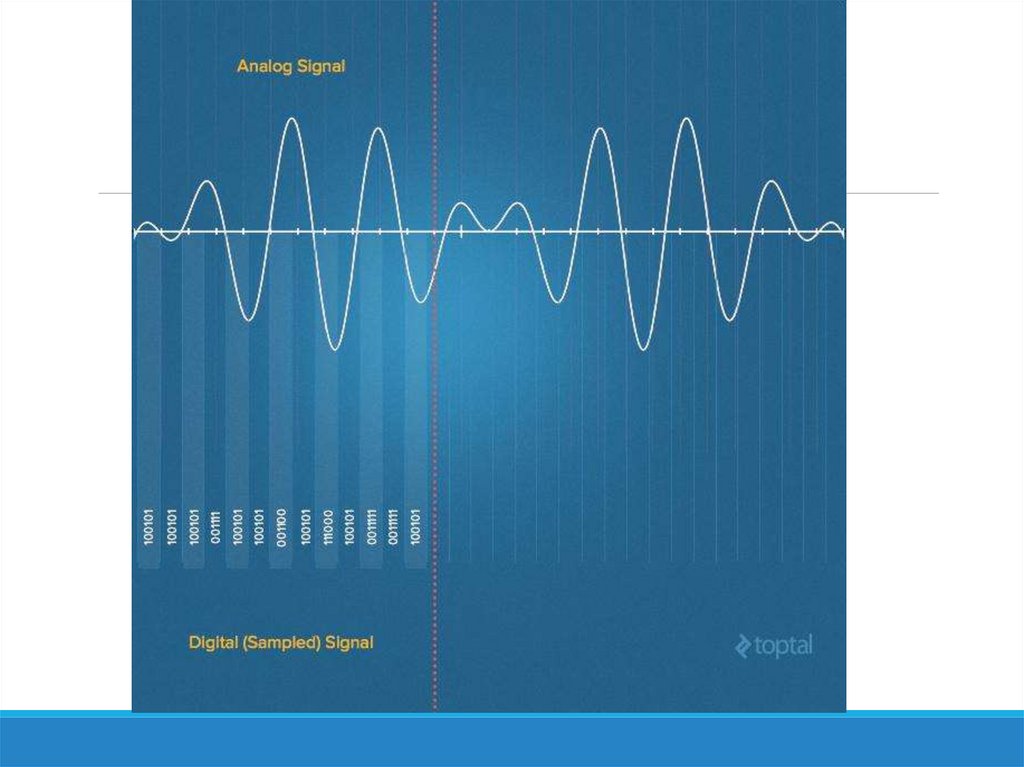
Під сигналом будемо розуміти звуковий
сигнал та генерувати його за допомогою
звукового редактора

24.

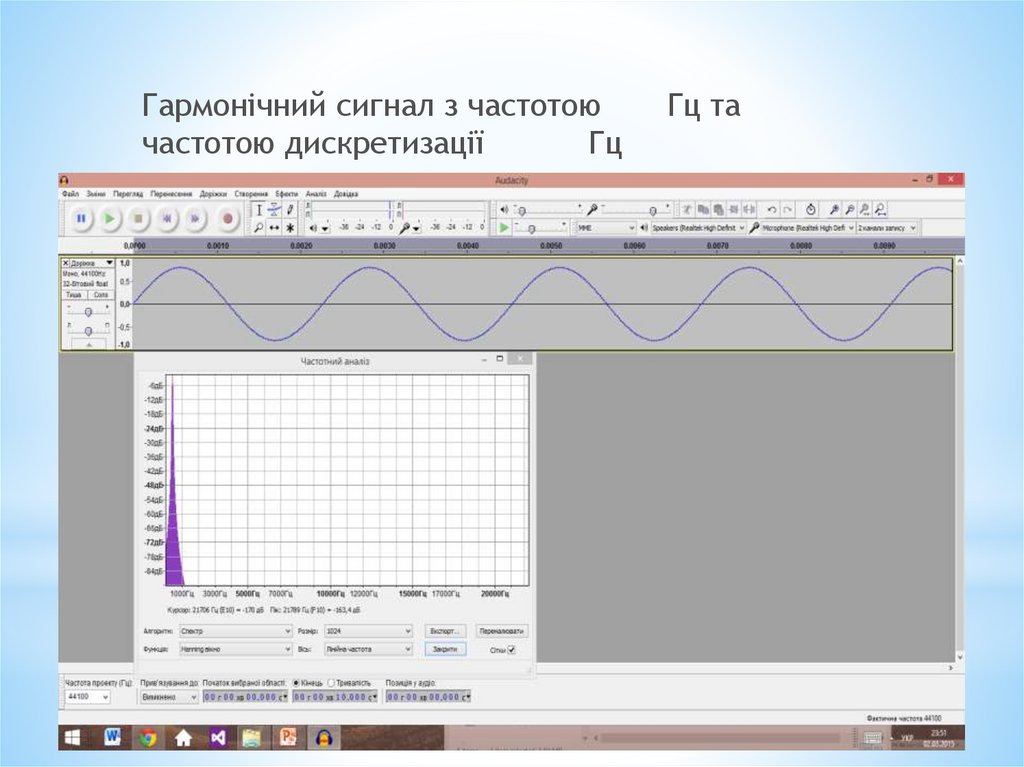
Гармонічний сигнал з частотою
частотою дискретизації
Гц
Гц та

25.

Спектр прямокутних імпульсів з частотою
та частотою дискретизації
Гц
Гц
*

26.

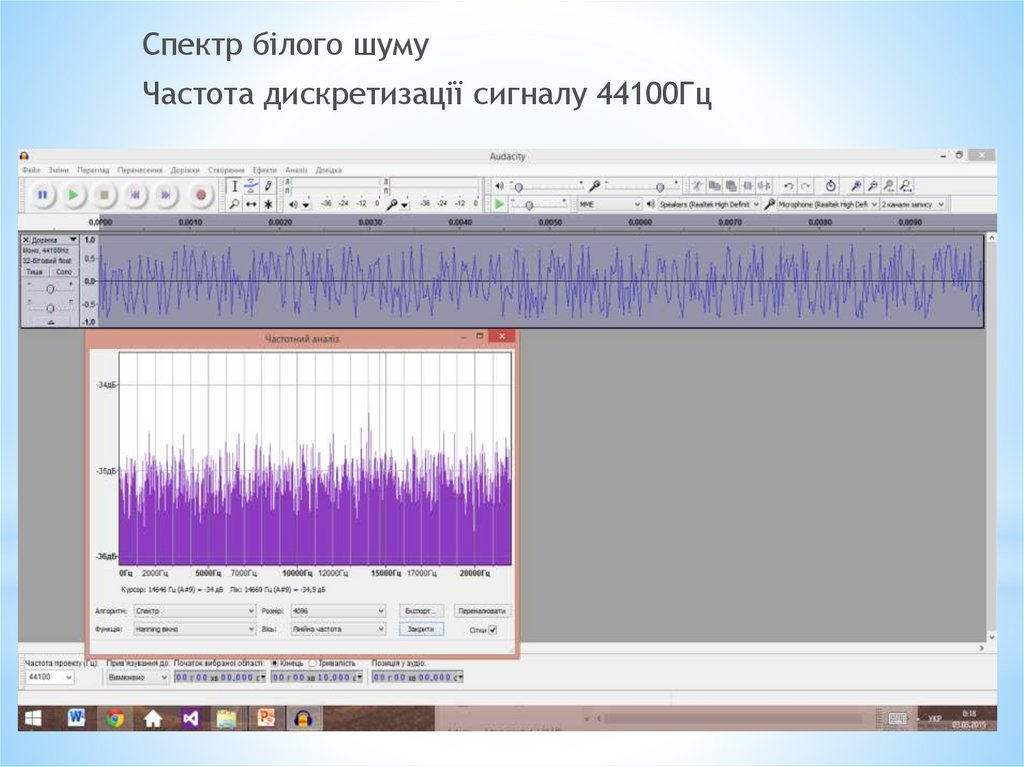
Спектр білого шуму
Частота дискретизації сигналу 44100Гц

27.

Рікі Мартін Live in La Vida Loka

28.

Дякую за увагу!