Задача о скатывании симметричного тела с наклонной плоскости без проскальзывания. 3 подхода

1. Механика 4

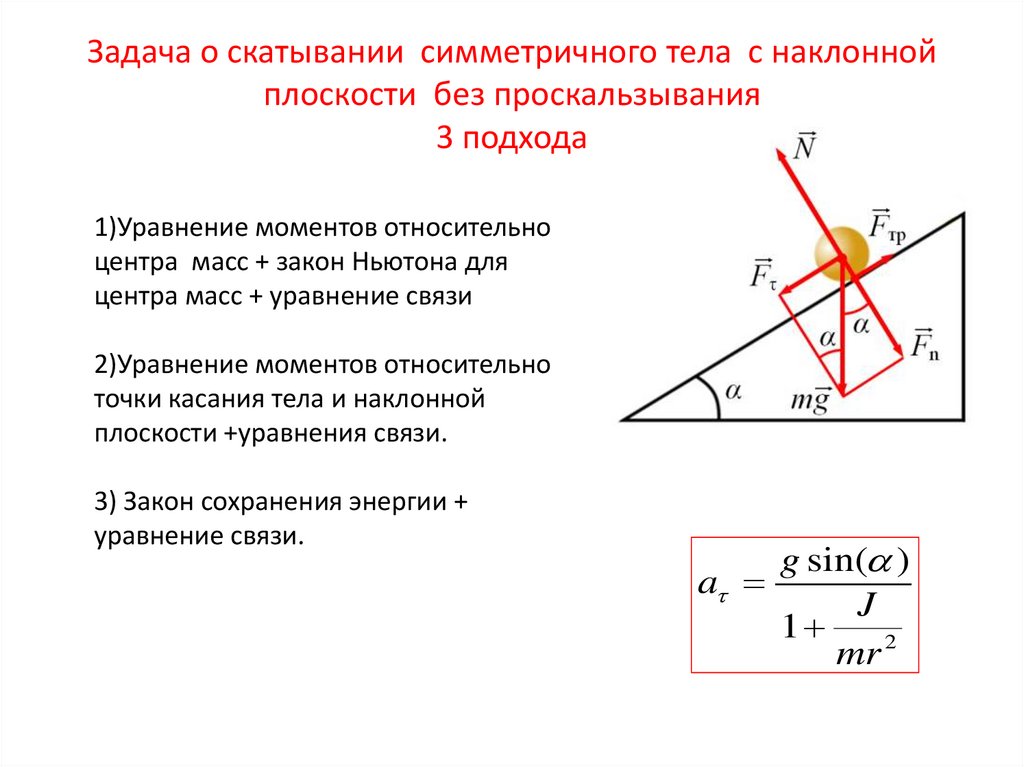
2. Задача о скатывании симметричного тела с наклонной плоскости без проскальзывания 3 подхода

1)Уравнение моментов относительно
центра масс + закон Ньютона для
центра масс + уравнение связи
2)Уравнение моментов относительно
точки касания тела и наклонной
плоскости +уравнения связи.
3) Закон сохранения энергии +
уравнение связи.
g sin( )
a
J
1
mr 2

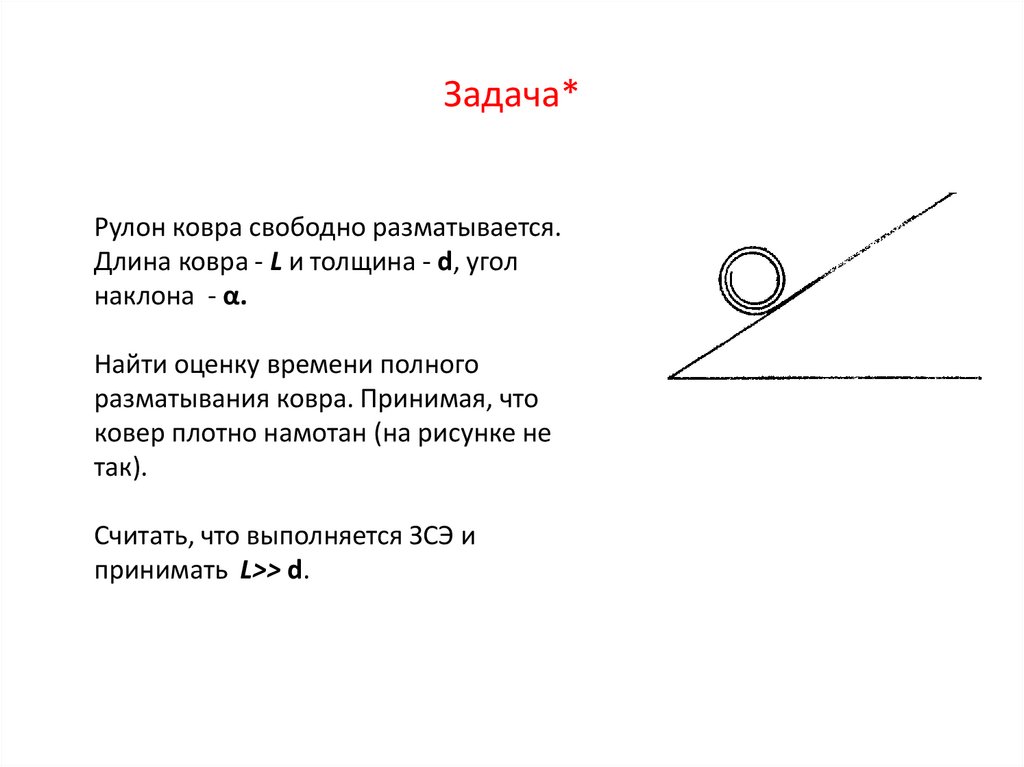
3. Задача*

Рулон ковра свободно разматывается.
Длина ковра - L и толщина - d, угол
наклона - α.
Найти оценку времени полного
разматывания ковра. Принимая, что
ковер плотно намотан (на рисунке не
так).
Считать, что выполняется ЗСЭ и
принимать L>> d.

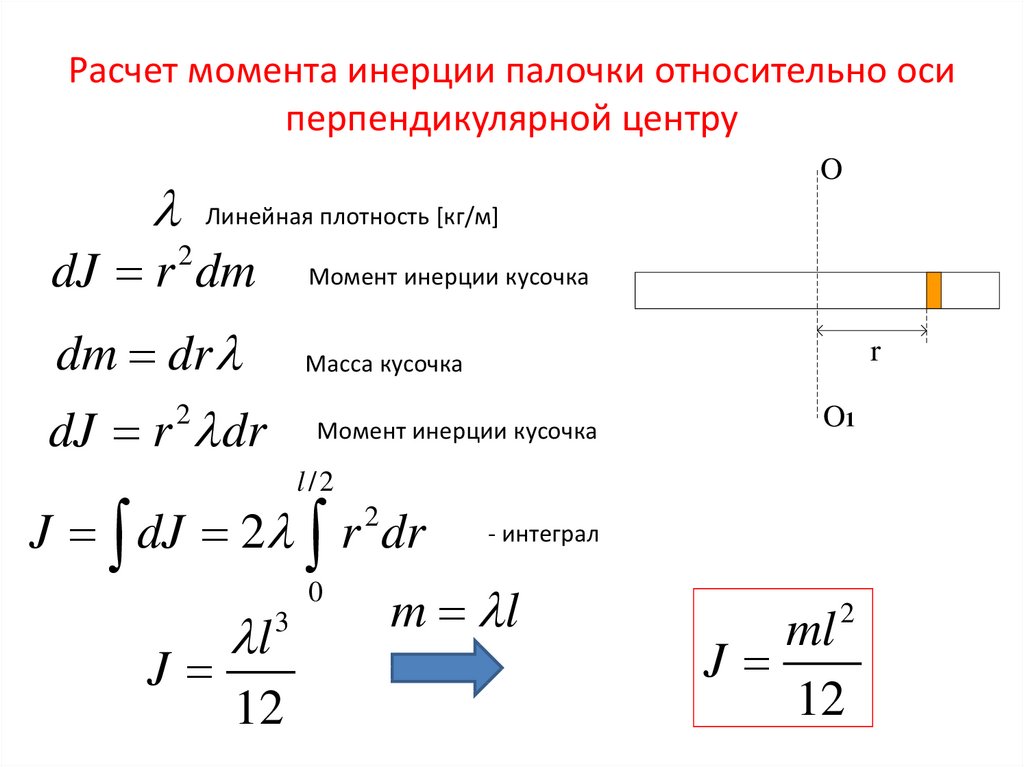
4. Расчет момента инерции палочки относительно оси перпендикулярной центру

O
Линейная плотность [кг/м]
dJ r dm
Момент инерции кусочка
dm dr
Масса кусочка
2
dJ r dr
2
r
Момент инерции кусочка
O1
l /2
J dJ 2 r dr
2
J
l
0
3
12
- интеграл
m l
2
ml
J
12

5. Расчет момента инерции диска относительно оси перпендикулярной центру симметрии

поверхностная плотность [кг/м2]
dJ r dm
2
Момент инерции кольца
dm 2 rdr
Масса кольца
dJ r 2 2 rdr
Момент инерции кольца
R
J dJ 2 r dr
3
J
R
2
4
0
интеграл
m R
2
mR
J
2
2

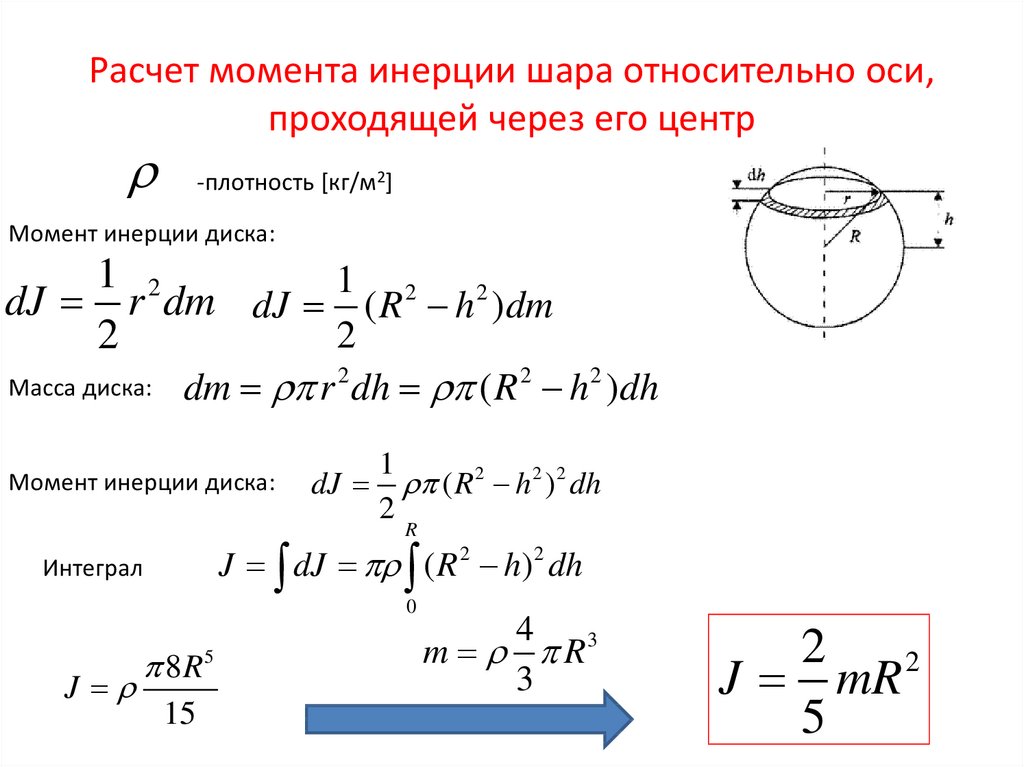
6. Расчет момента инерции шара относительно оси, проходящей через его центр

-плотность [кг/м2]
Момент инерции диска:
1 2
1 2
dJ r dm dJ ( R h 2 )dm
2
2
Масса диска:
dm r 2 dh ( R 2 h 2 )dh
Момент инерции диска:
dJ
1
( R 2 h 2 ) 2 dh
2
R
J dJ ( R 2 h) 2 dh
Интеграл
0
J
8R5
15
4
m R3
3
2
2
J mR
5

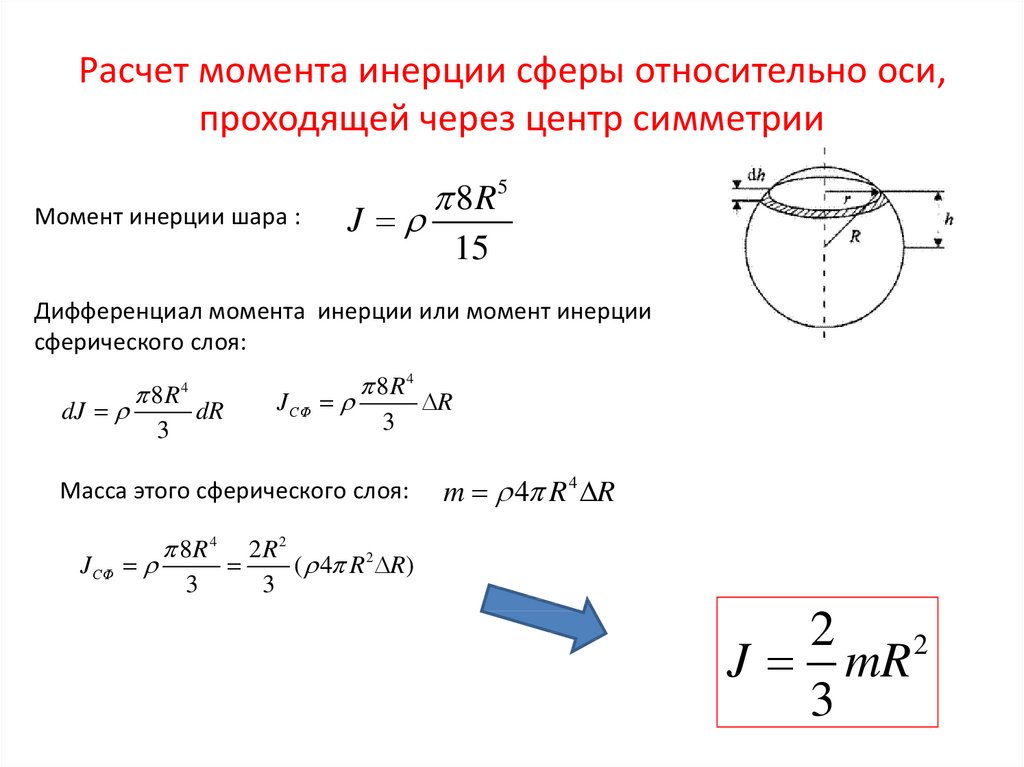
7. Расчет момента инерции сферы относительно оси, проходящей через центр симметрии

Момент инерции шара :
J
8R5
15
Дифференциал момента инерции или момент инерции
сферического слоя:
dJ
8R 4
3
dR
J СФ
8R 4
3
Масса этого сферического слоя:
J СФ
8R 4
3
R
m 4 R 4 R
2R2
( 4 R 2 R)
3
2
2
J mR
3

8.

Уравновешенный гироскоп – быстро вращающееся тело,
имеющее три степени свободы
8

9. Прецессия гироскопа*

dL
M
dt
L -момент импульса гороскопа, M - момент внешней силы
L -момент импульса гороскопа велик и относительно мало меняется,
то можно записать:
[ L] M
Ω – Угловая скорость прецессии

10. Куда катится катушка, которую тянут за нить (проскальзывания нет)?

v *cos( ) r u
v R 0
Проекция скорости
катушки на нить
Уравнение связи
uR
v
R cos( ) r

11. Диссипативные силы

Диссипативные силы – силы, зависящие от скорости, работа которых
может приводить к уменьшению общей энергии системы.

12. Сухое трение: закон Кулона –Амонтона

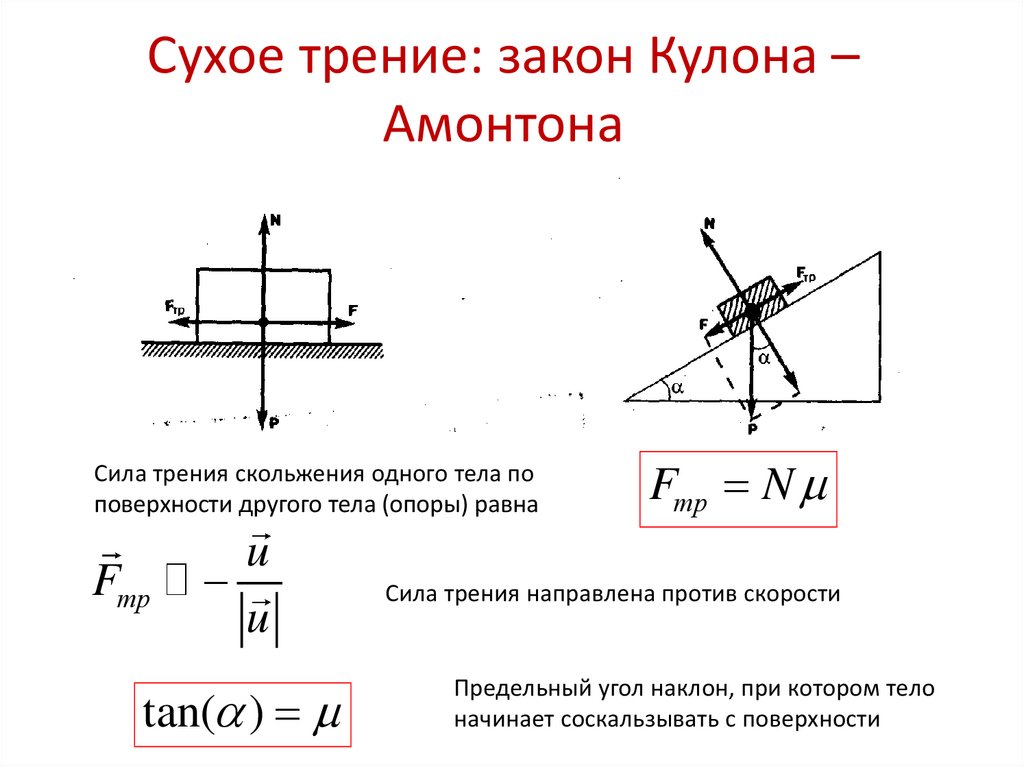
Сухое трение: закон Кулона –
Амонтона
Сила трения скольжения одного тела по
поверхности другого тела (опоры) равна
Fтр
u
u
tan( )
Fтр N
Сила трения направлена против скорости
Предельный угол наклон, при котором тело
начинает соскальзывать с поверхности

13. Сухое трение – закон Кулона –Амонтона

Сухое трение – закон Кулона –
Амонтона
Теория
Эксперимент
Таблица: Коэффициенты трения

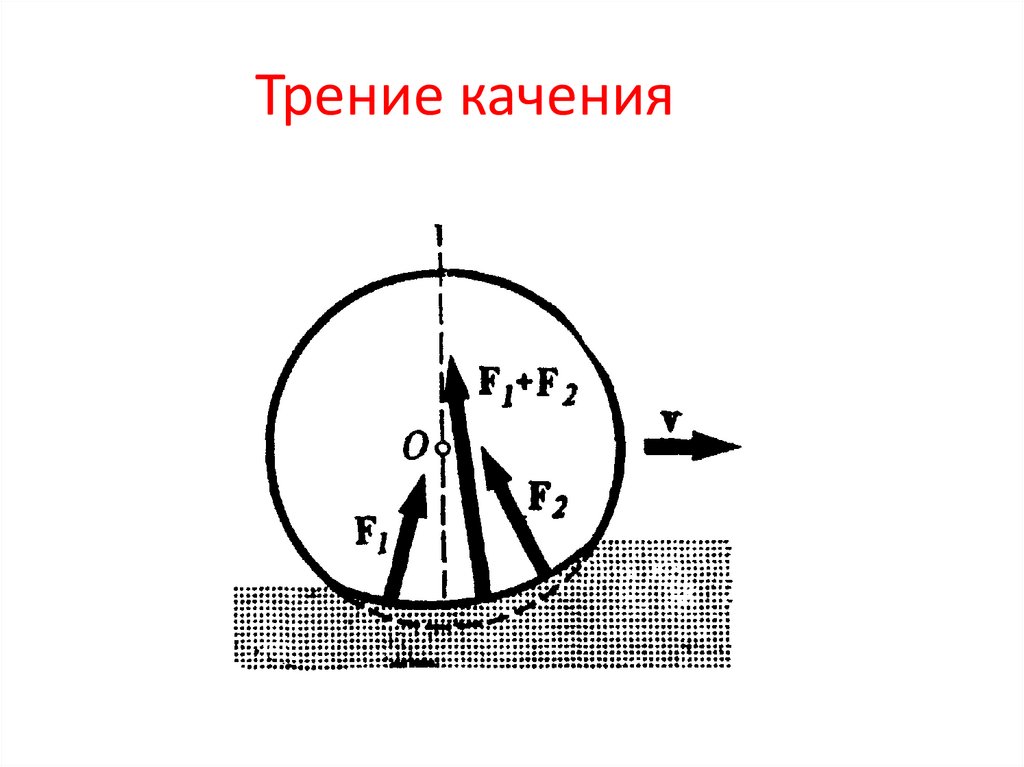
14. Трение качения

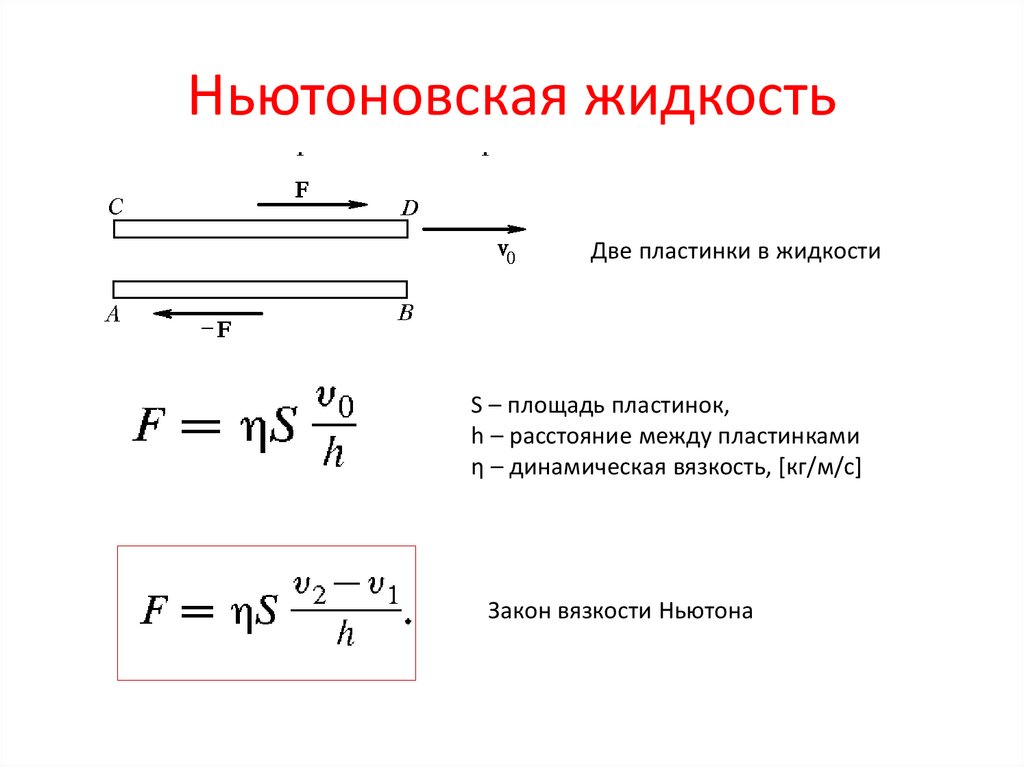
15. Ньютоновская жидкость

Две пластинки в жидкости
S – площадь пластинок,
h – расстояние между пластинками
η – динамическая вязкость, [кг/м/c]
Закон вязкости Ньютона

16. Вязкость кинематическая и динамическая

η – динамическая вязкость, [кг/м/c]
0
– кинематическая вязкость, [м2/c]
Идеальная жидкость – жидкость с нулевой вязкостью

17. Число Рейнольдса

lu
Re
lu
Re
K
A
l – характерные размеры
u – характерная скорость
К– кинетическая энергия
А– вязкая работа
l 3u 2 / 2
K
A u l 2
1>>Re доминирует вязкость
Re>>1 доминирует инерционность

18. Число Рейнольдса

lu
Re
lu
Re
K
A
l – характерные размеры
u – характерная скорость
К– кинетическая энергия
А– вязкая работа
l 3u 2 / 2
K
A u l 2
1>>Re доминирует вязкость
Re>>1 доминирует инерционность

19. Силы сопротивления: низкие скорости

Ftr f (l , u , )
Ftr
Re<<1 доминирует вязкость
l * u *
кг * м
[ м] [ м / c] *[кг / м / c] * f (Re)
2
с
Ftr
1
1
1
lu
Ftr 6 Ru
Точная формула сила трения при обтекании шара
Формула Стокса

20. Силы сопротивления: высокие скорости

Ftr f (l , u , )
Ftr
Re>>1 доминирует инерционность
l * u *
кг * м
[ м] [ м / c] *[кг / м3 ]
2
с
Ftr
lu
2
2
(NB) Точных решений нет!
1
2
2

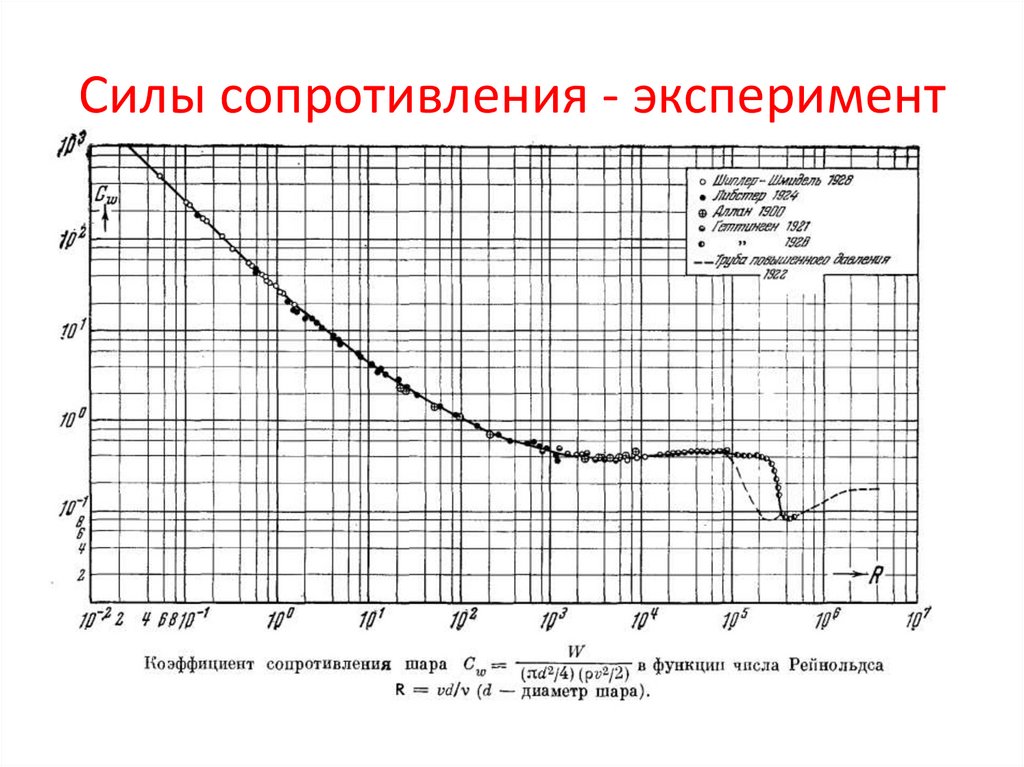
21. Силы сопротивления - эксперимент

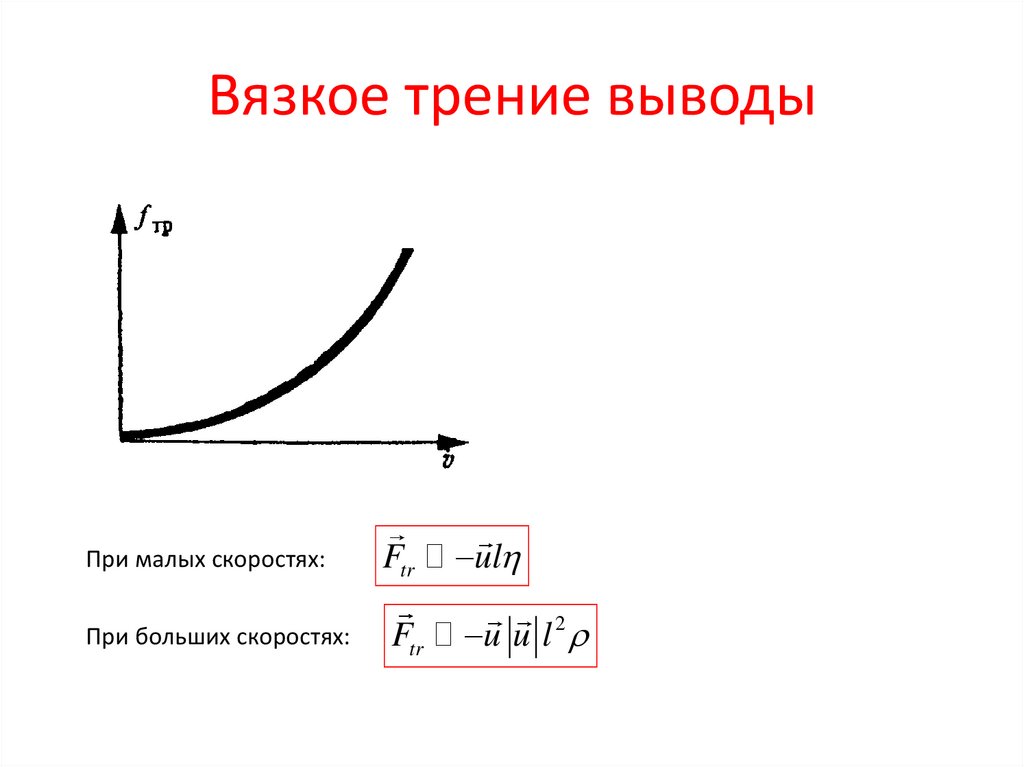
22. Вязкое трение выводы

При малых скоростях:
При больших скоростях:
Ftr
ul
Ftr
u u l 2

23. Задача*

Пусть в среде действует сила трения, зависящая от скорости u,
, где α - некоторый показатель степени.
Рассмотреть, как зависит путь тормозящейся частицы
до остановки от показателя степени α.
Ftr ~ u