Похожие презентации:
Центр масс твердого тела. Импульс твердого тела
1. центр масс твердого тела. Импульс твердого тела.
ЦЕНТР МАССТВЕРДОГО ТЕЛА.
ИМПУЛЬС ТВЕРДОГО
ТЕЛА.
2. Центр масс
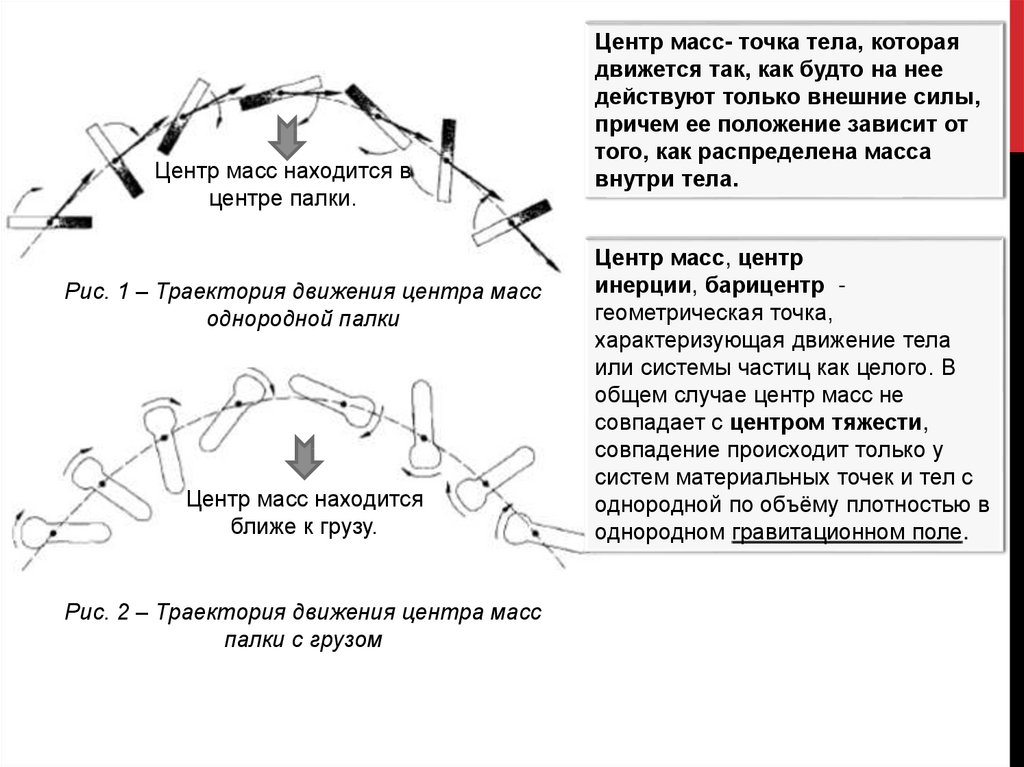
находится вцентре палки.
Рис. 1 – Траектория движения центра масс
однородной палки
ЦЕНТР МАСС
Центр масс находится
ближе к грузу.
Рис. 2 – Траектория движения центра масс
палки с грузом
Центр масс- точка тела, которая
движется так, как будто на нее
действуют только внешние силы,
причем ее положение зависит от
того, как распределена масса
внутри тела.
Центр масс, центр
инерции, барицентр геометрическая точка,
характеризующая движение тела
или системы частиц как целого. В
общем случае центр масс не
совпадает с центром тяжести,
совпадение происходит только у
систем материальных точек и тел с
однородной по объёму плотностью в
однородном гравитационном поле.
3.
Центр масс тела не следует путать с центром тяжести.Центром тяжести механической системы называется точка,
относительно которой суммарный момент
сил тяжести(действующих на систему) равен нулю. Например,
в системе, состоящей из двух одинаковых масс, соединённых
несгибаемым стержнем, и помещённой в
неоднородное гравитационное поле (например, планеты),
центр масс будет находиться в середине стержня, в то время
как центр тяжести системы будет смещён к тому концу
стержня, который находится ближе к планете
(ибо вес массы P = m·g зависит от параметра
гравитационного поля g), и, вообще говоря, даже расположен
вне стержня.
4. Центр масс
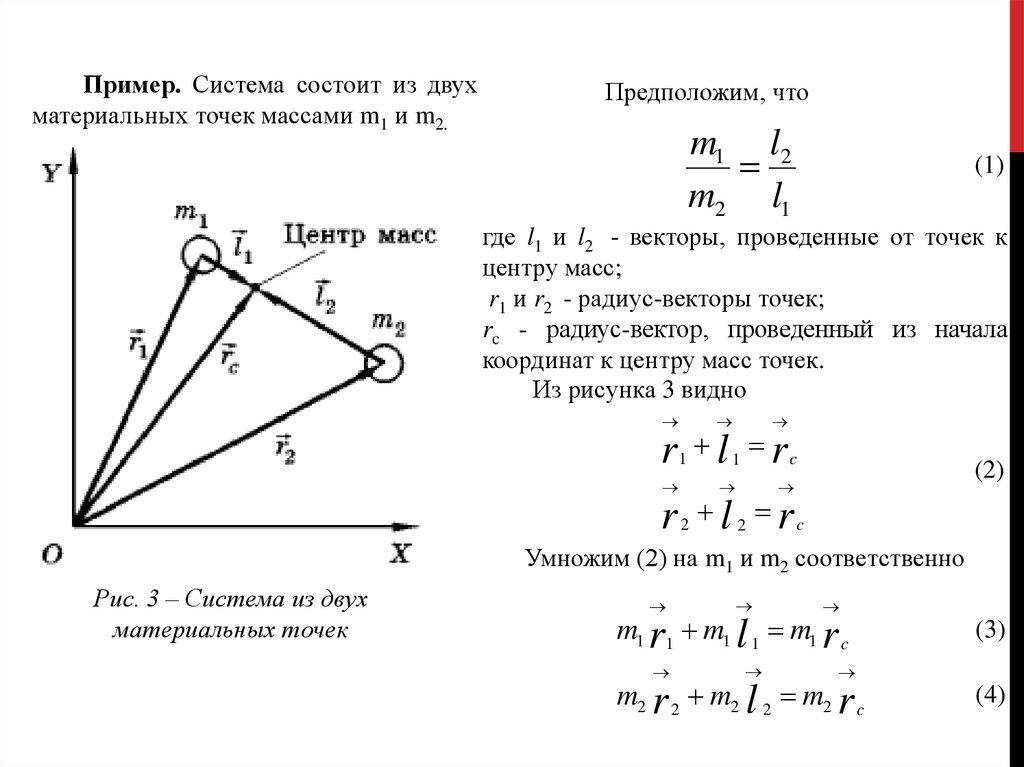
ЦЕНТР МАССПример. Система состоит из двух
материальных точек массами m1 и m2.
Предположим, что
m1 l2
m2 l1
(1)
где l1 и l2 - векторы, проведенные от точек к
центру масс;
r1 и r2 - радиус-векторы точек;
rc - радиус-вектор, проведенный из начала
координат к центру масс точек.
Из рисунка 3 видно
r1 l 1 r c
(2)
r2 l 2 rc
Умножим (2) на m1 и m2 соответственно
Рис. 3 – Система из двух
материальных точек
m1 r 1 m1 l 1 m1 r c
(3)
m2 r 2 m2 l 2 m2 r c
(4)
5. Центр масс
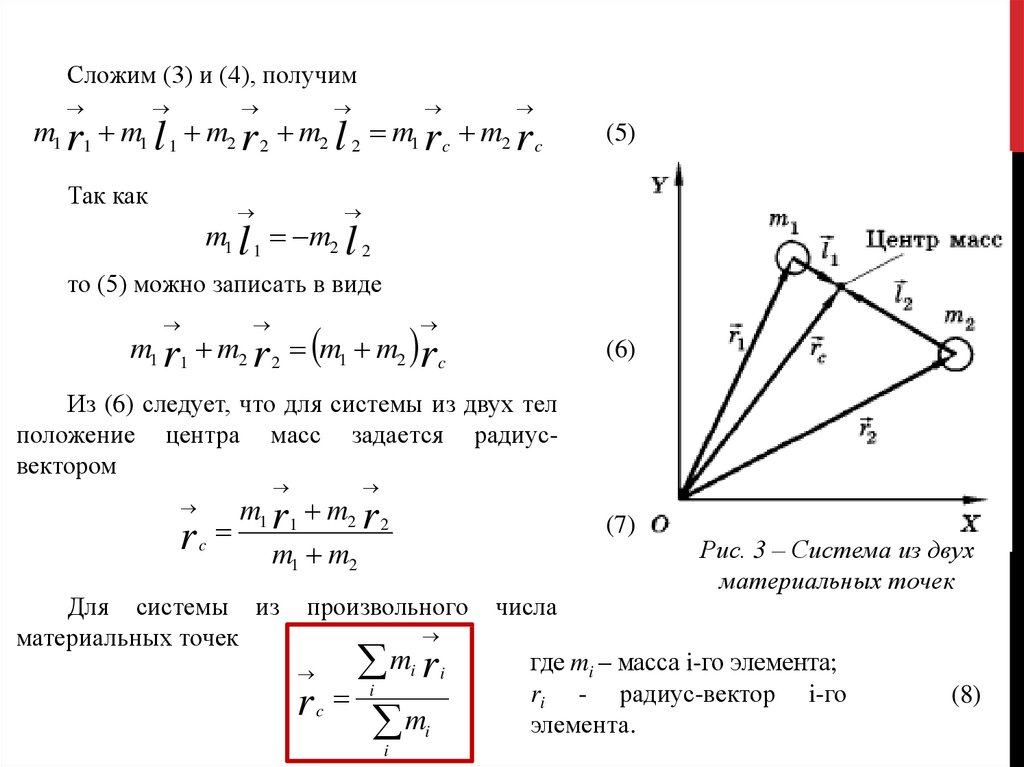
ЦЕНТР МАСССложим (3) и (4), получим
m1 r1 m1 l 1 m2 r 2 m2 l 2 m1 r c m2 r c
Так как
(5)
m1 l 1 m2 l 2
то (5) можно записать в виде
m1 r1 m2 r 2 m1 m2 r c
(6)
Из (6) следует, что для системы из двух тел
положение центра масс задается радиусвектором
rc
m1 r 1 m2 r 2
m1 m2
Для системы из
материальных точек
(7)
произвольного
числа
Рис. 3 – Система из двух
материальных точек
i mi r i
rc m
i
i
где mi – масса i-го элемента;
ri - радиус-вектор i-го
элемента.
(8)
6. Центр масс
ЦЕНТР МАССi mi xi
xc
i mi
i mi уi
уc
i mi
i mi zi
zc
i mi
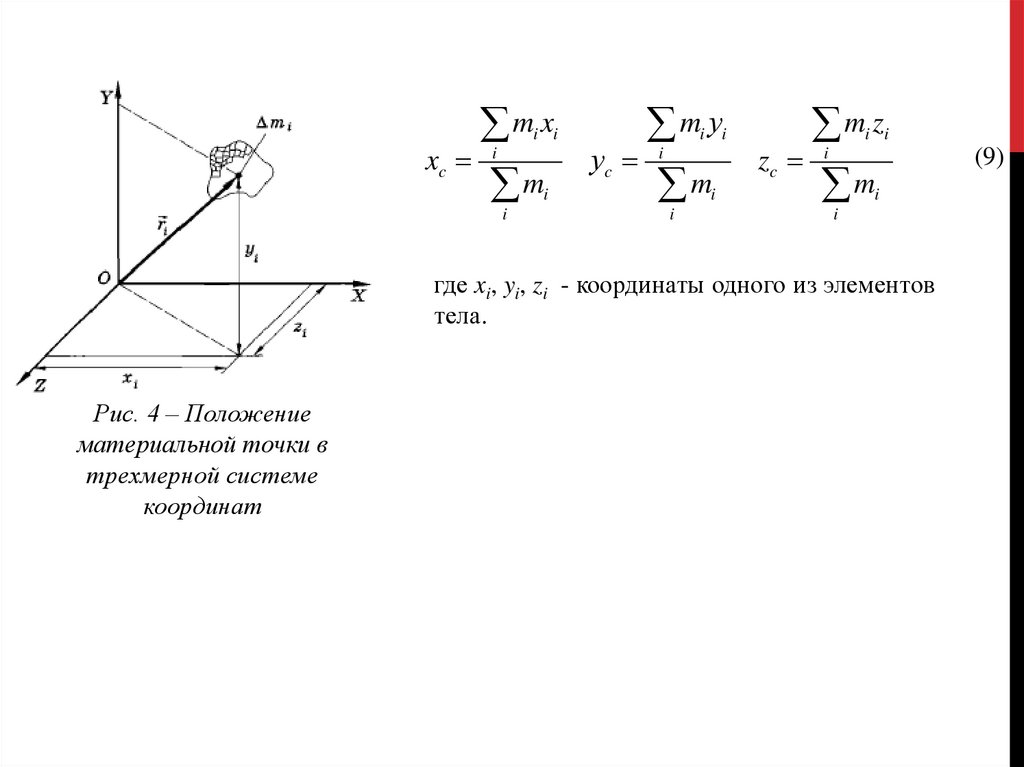
где xi, yi, zi - координаты одного из элементов
тела.
Рис. 4 – Положение
материальной точки в
трехмерной системе
координат
(9)
7. Импульс твердого тела.
ИМПУЛЬС ТВЕРДОГО ТЕЛА.Импульс твердого тела равен импульсу материальной точки
той же массы, скорость которой равна скорости центра масс
тела.
По определению импульс твердого тела равен суммарному
импульсу всех его точек.
Центр масс твердого тела движется так же как двигалась бы
материальная точка, масса которой равна массе тела, под
действием внешних сил, приложенных к данному телу.
p m
c
8.
Импульс твердого телаИмпульс твердого тела равен суммарному
импульсу всех его точек
p mi i
(10)
i
где vi – скорость отдельных точек тела.
С учетом (8) можно записать
m r c mi r i
(11)
i
Путь за время ∆t радиус-векторы изменятся
на ∆r
(12)
m c mi i
r
r
i
Разделим левую и правую части выражения
(12) на ∆t
m
rc
mi r i
t
t
i
(13)
m c mi i
i
(14)
p m
c
(15)
9.
Теорема о движении центра массУравнение движения i-го элемента массой mi
(mi i )
Fik Fi
t
t
k i
pi
(16)
F
–
сумма
внутренних
сил,
действующих на i-ый элемент тела со
стороны других элементов
По III закону Ньютона
ik
Fik Fki
(17)
Тогда сумма всех внутренних сил равна 0
i mi i
t
Fi
(20)
i
С учетом (14)
где Fi – внешняя сила,
k i
или
(18)
Тогда (16) можно записать в виде
(mi i )
i t i Fi
(19)
(21)
m c
Fi
t
i
(22)
m a c Fi
i
Fik Fki 0
m c
Fi
t
i
(23)
10.
Теорема о движении центра массСледствие теоремы о движении центра масс:
Если сумма внешних сил равна 0, то центр масс покоится или
движется равномерно и прямолинейно.
c
0
t
c const
(24)






 Физика
Физика








