Методы параметрического спектрального анализа. Параметрические модели сигналов

1. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»

Методы параметрического
спектрального анализа.
Параметрические модели
сигналов
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)

2. АРСС, АР И СС-МОДЕЛИ (1)

1) АРСС-модель: модель авторегрессии скользящего среднего;
2) АР-модель: модель авторегрессии;
3) СС-модель: модель скользящего среднего.
АРСС-модель описывается разностным уравнением БИХ-фильтра
(фильтр с бесконечной импульсной характеристикой).
M 1
N 1
k 1
i 0
y(n) ak y(n k ) bi e(n i)
e(n) входной сигнал БИХ-фильтра (нормальный белый шум)
y (n) выходной сигнал БИХ-фильтра
ak , bi параметры АРСС-модели
( M 1) порядок АРСС-модели
2

3. АРСС, АР И СС-МОДЕЛИ (2)

( N 1) порядок нерекурсивной части БИХ-фильтра
( M 1) порядок рекурсивной части БИХ-фильтра
АРСС-модели соответствует БИХ-фильтр с дробно-рациональной
передаточной функцией.
H ( z)
N 1
1 bi z i
i 1
M 1
1 ak z k
B( z )
A( z )
k 1
ak k 1 , bi i 1 параметры АРСС-модели
M 1
N 1
( N 1) порядок СС-части
( M 1) порядок АР-части
3

4. СТРУКТУРНАЯ СХЕМА АРСС-МОДЕЛИ

b0
e(n)
z-1
b1
y(n)
a1
z-1
z-1
z-1
b2
нерекурсивная часть
a2
рекурсивная часть
4

5. АР-МОДЕЛЬ

5
АР-МОДЕЛЬ
Разностное уравнение АР-модели
M 1
y(n) ak y(n k ) e(n)
k 1
ak k 1
M 1
параметры АР-модели
( N 1) порядок АР-модели
АР-модели соответствует БИХ-фильтр полюсного вида ("чисто
рекурсивный" фильтр).
H ( z)
1
M 1
1 ak z k
k 1
1
A( z )

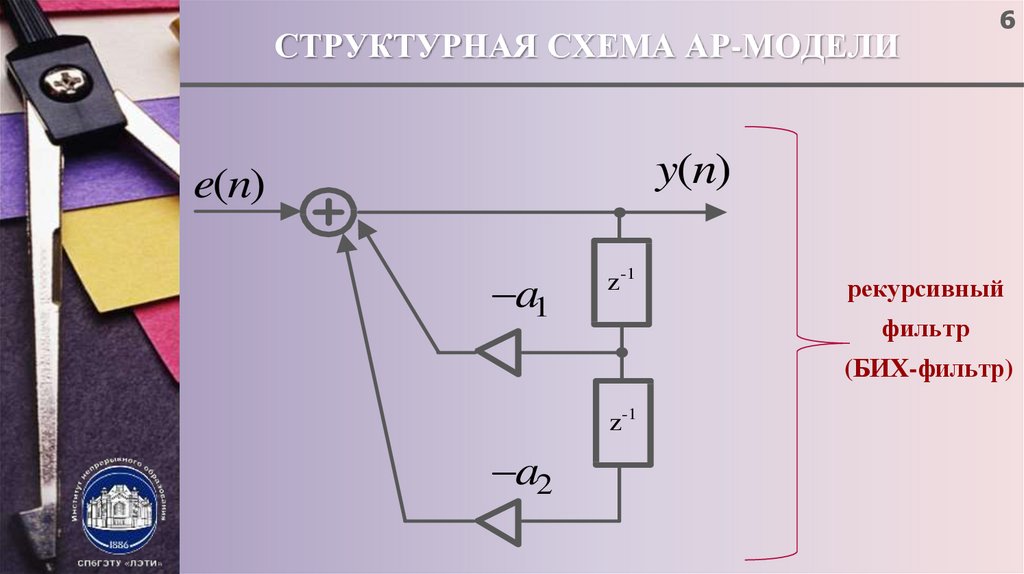
6. СТРУКТУРНАЯ СХЕМА АР-МОДЕЛИ

6
y(n)
e(n)
a1
z-1
рекурсивный
фильтр
(БИХ-фильтр)
z-1
a2

7. СС-МОДЕЛЬ (1)

Разностное уравнение СС-модели
N 1
y(n) e(n) bi e(n i)
bi i 1
N 1
i 1
параметры СС-модели
( N 1) порядок СС-модели
СС-модели соответствует КИХ-фильтр с передаточной функцией
N 1
H ( z ) 1 bi z i B( z )
i 1
7

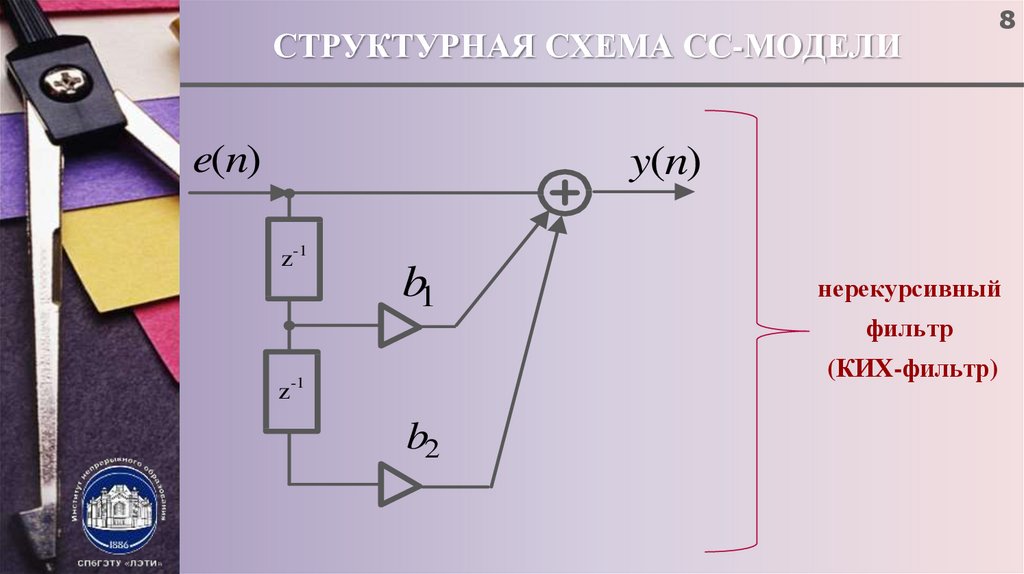
8. СТРУКТУРНАЯ СХЕМА СС-МОДЕЛИ

e(n)
8
y(n)
z-1
b1
нерекурсивный
фильтр
(КИХ-фильтр)
-1
z
b2

9. СС-МОДЕЛЬ (2)

СС-модели соответствует КИХ-фильтр с передаточной функцией.
N 1
H ( z ) 1 bi z i B( z )
i 1
СПМ моделируемой последовательности
σ2
jωT 2
S y (ω)
H (e )
fд
1 f д постоянный множитель
(для согласования размерностей СПМ)
σ 2 дисперсия входного нормального белого шума
H (e jωT ) комплексная частотная характеристика
эквивалентного КИХ-фильтра
9

10. РАСЧЕТ ОЦЕНКИ СПМ

10
Процедура расчета оценки СПМ
1) выбор класса модели (АР, СС, АРСС);
2) оценка порядка модели;
3) оценка параметров модели;
4) расчет оценки СПМ.
Выбору модели должна предшествовать проверка на адекватность
анализируемому сигналу (используются специальные критерии).
На практике наиболее распространена АР-модель.
адекватность широкому классу сигналов;
наименьшие вычислительные затраты.

11. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»

Методы параметрического
спектрального анализа.
Параметрические модели
сигналов
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)