Похожие презентации:
Нахождение угла между скрещивающимися прямыми
1. Нахождение угла между скрещивающимися прямыми.
Решение задач уровня С.2. Аргументы. 1). Определение скрещивающихся прямых. 2). Определение угла между скрещивающимися прямыми. 3). Признак
скрещивающихся прямых.4). Теорема Пифагора.
5). Свойство высоты равнобедренного треугольника, проведенной
к основанию.
6). Определение правильной призмы.
7). Определение синуса острого угла прямоугольного треугольника.
8). Определение косинуса острого угла прямоугольного треугольника.
9). Определение правильного многоугольника.
10). Теорема о сумме углов выпуклого многоугольника.
11). Свойство окружности, описанной около правильного
шестиугольника.
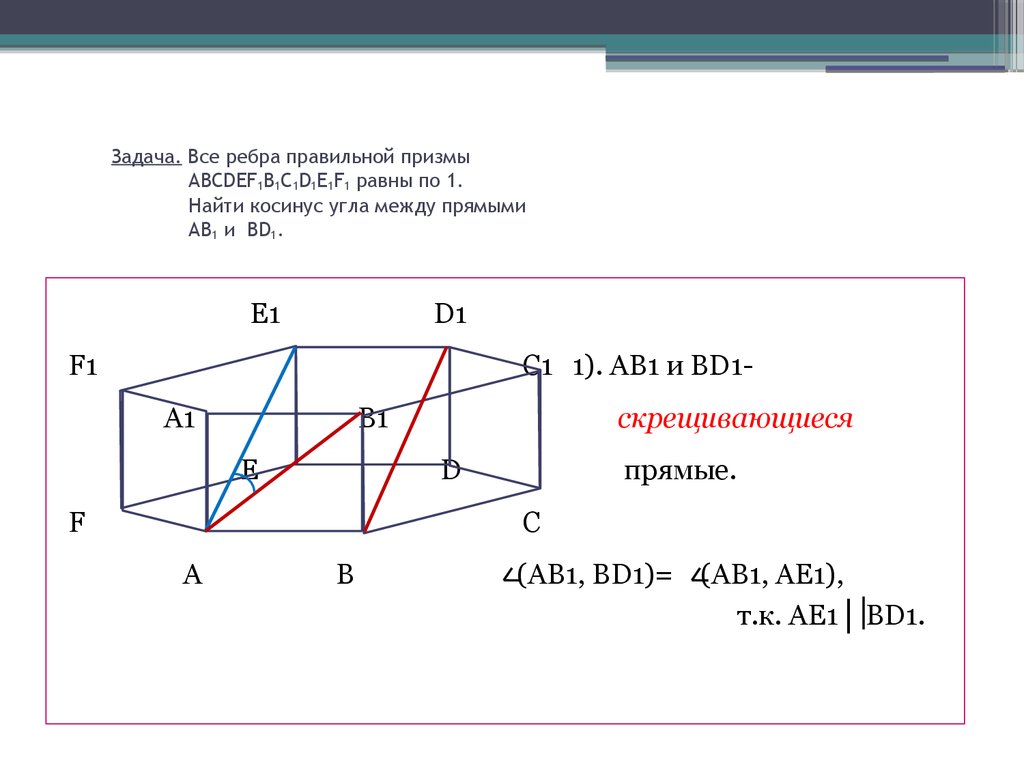
3. Задача. Все ребра правильной призмы ABCDEF1B1C1D1E1F1 равны по 1. Найти косинус угла между прямыми AB1 и BD1.
E1D1
F1
C1 1). AB1 и BD1A1
B1
E
скрещивающиеся
D
F
прямые.
C
A
B
(AB1, BD1)= (AB1, AE1),
т.к. AE1│ BD1.
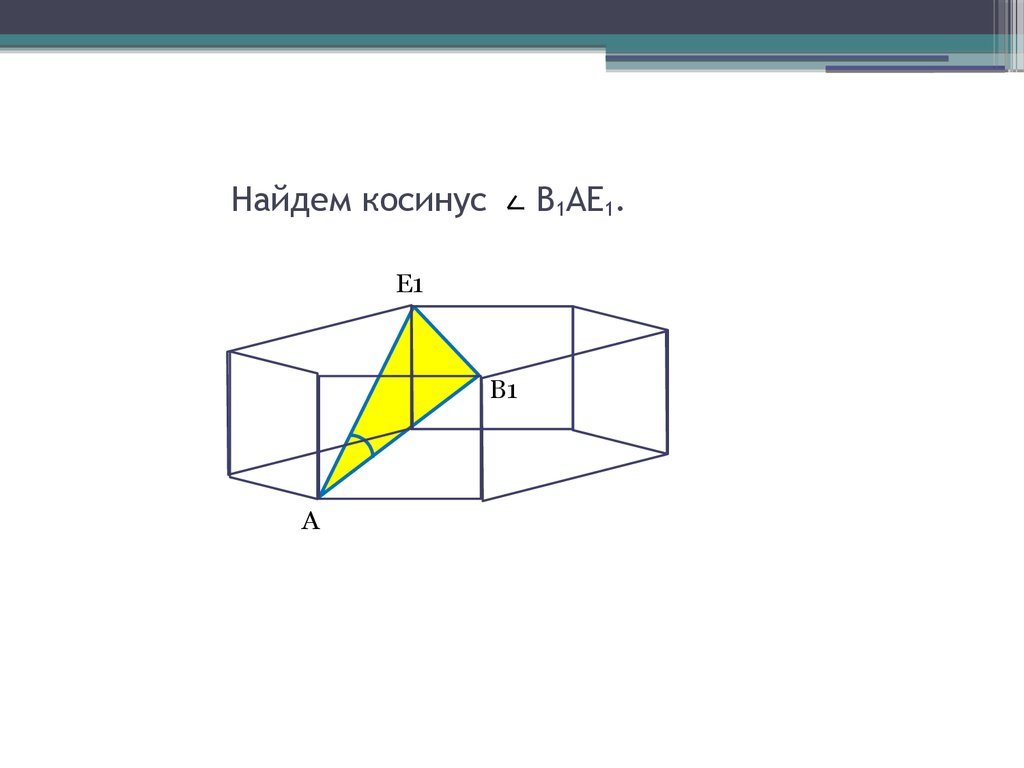
4. Найдем косинус B1AE1.
Е1В1
А
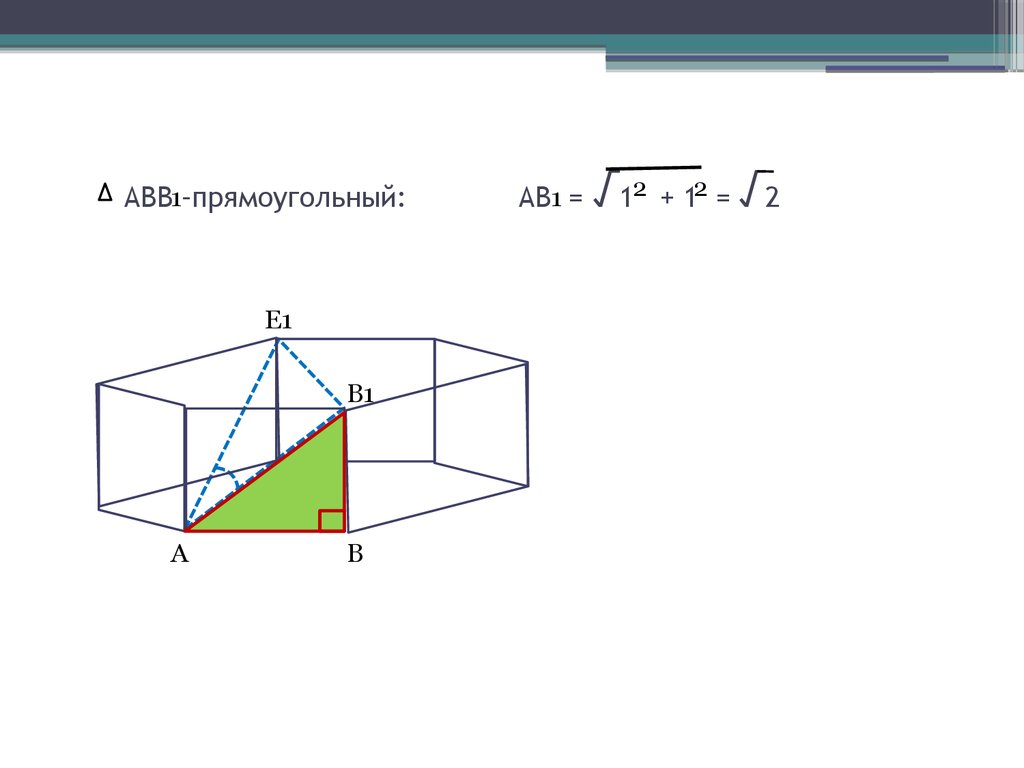
5. АВВ –прямоугольный: АВ = √1 + 1 = √2
АВВ1–прямоугольный:Е1
В1
А
В
АВ1 =
√12 + 12 = √2
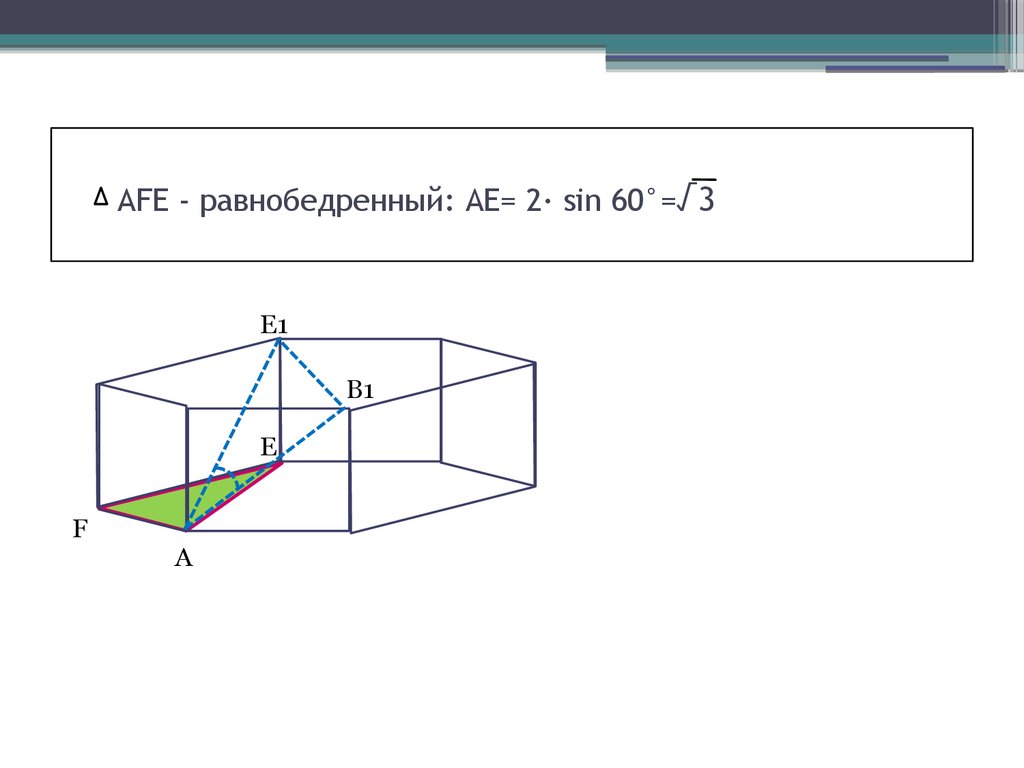
6. AFE - равнобедренный: АЕ= 2· sin 60°=√3
E1В1
E
F
A
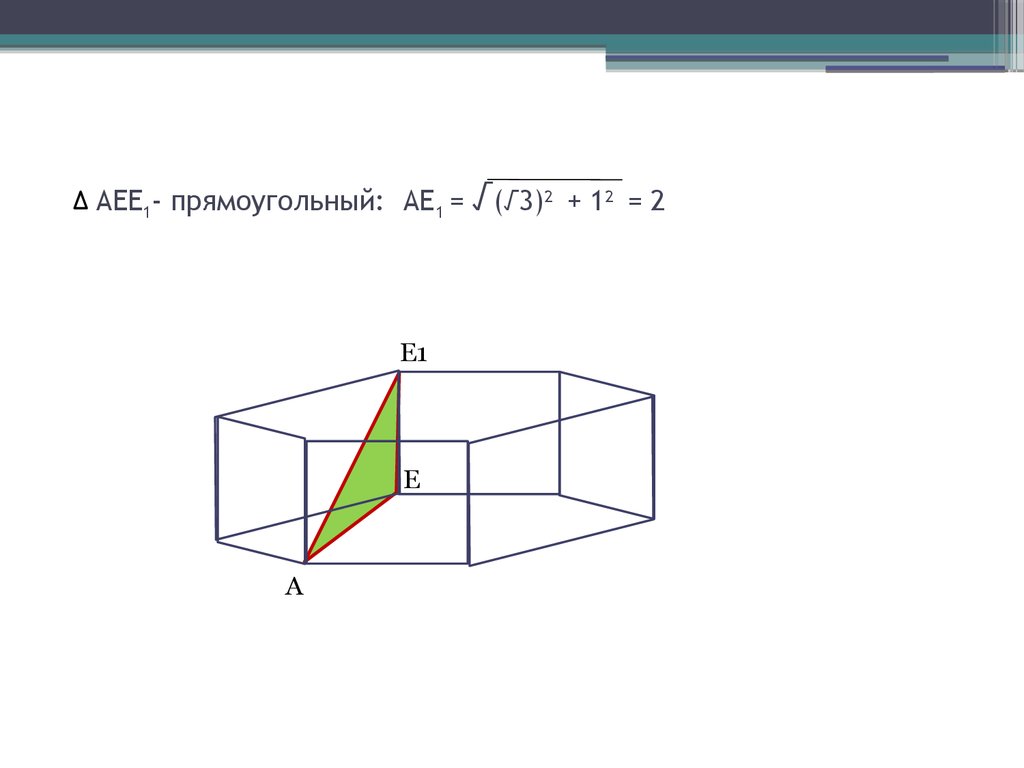
7. AEE1- прямоугольный: АЕ1 = √(√3)2 + 12 = 2
AEE1- прямоугольный: АЕ1 =E1
E
A
√(√3)2
+ 12 = 2
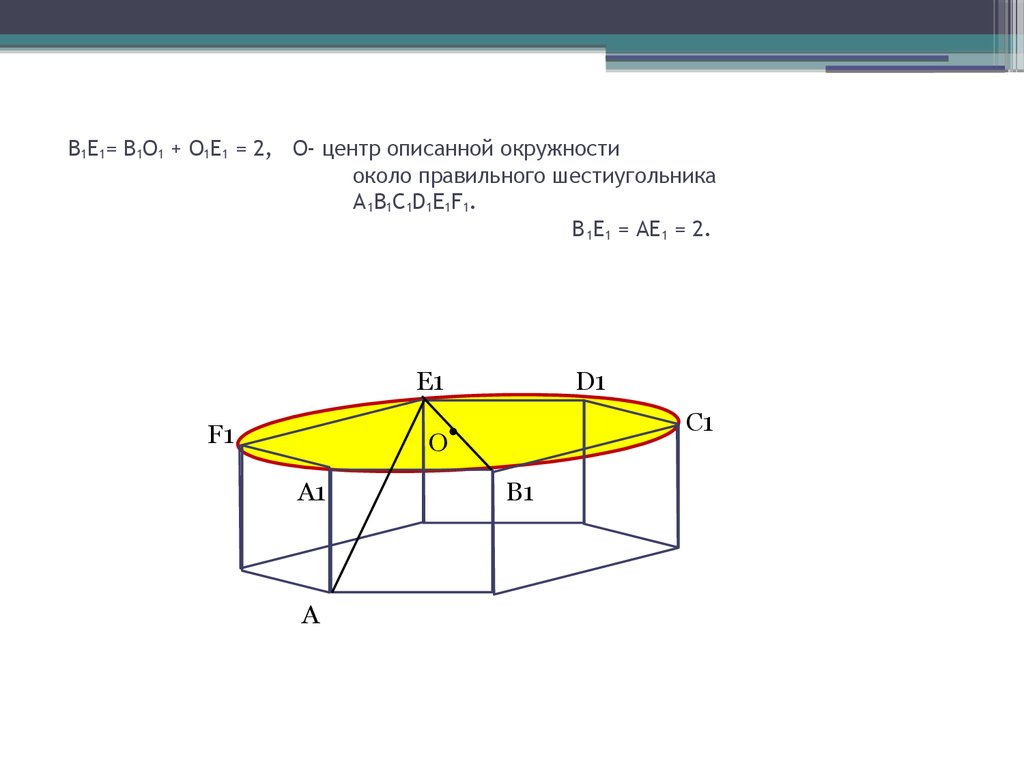
8. В1Е1= В1О1 + О1Е1 = 2, О- центр описанной окружности около правильного шестиугольника A1B1C1D1E1F1. В1Е1 = АЕ1 = 2.
В1Е1= В1О1 + О1Е1 = 2, О- центр описанной окружностиоколо правильного шестиугольника
A 1B1C1D1E1F1.
В 1Е1 = АЕ1 = 2.
E1
F1
D1
C1
O
A1
A
B1
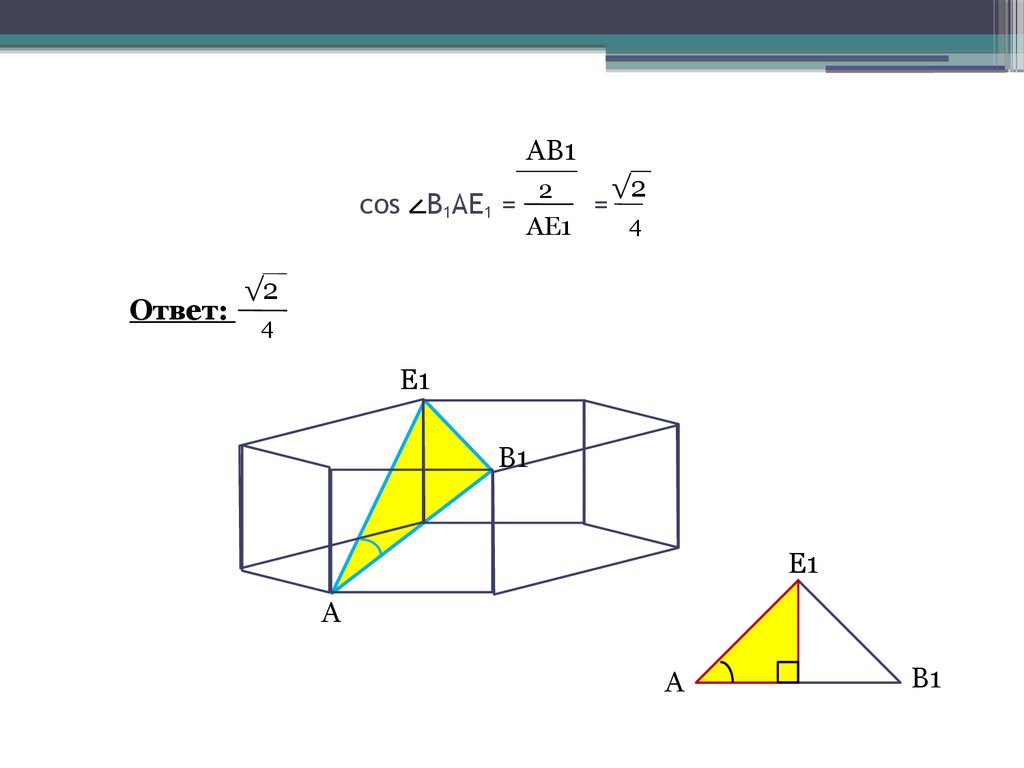
9. cos В1АЕ1 = =
АВ1cos В1АЕ1 =
Ответ:
√2
2
=
4
АЕ1
√2
4
Е1
В1
Е1
А
А
В1


 Математика
Математика








