Электростатика. Диэлектрики. Диэлектрическая поляризация. (Лекция 3)

1.

Кафедра физики
Лекция 3
ЭЛЕКТРОСТАТИКА
ПЛАН ЛЕКЦИИ
1. Диэлектрики. Диэлектрическая поляризация.
2. Электрическое поле внутри диэлектрика.
3. Теорема Гаусса при наличии диэлектриков.
4. Вектор электрического смещения.
5. Постулат Максвелла.
6. Условия на границе двух диэлектриков
Общая физика. «Электростатика»

2.

ДИЭЛЕКТРИКИ
Кафедра физики
Электрические свойства среды определяются реакцией заряженных
частиц на внешнее электрическое поле
Под действием внешнего поля могут быть следующие виды
движения частиц вещества:
1. Ограниченное движение зарядов
Заряды называются связанными, в результате их движения
(смещения) происходит диэлектрическая поляризация вещества.
Вещества, у которых под действием электрического поля преобладающим
является процесс смещения связанных зарядов, называются диэлектриками.
2. Неограниченное перемещение зарядов в объеме вещества.
Заряды называются свободными, в результате их движения
возникает электрический ток
Вещества, у которых под действием электрического поля преобладающим
является процесс неограниченного движения зарядов,
называются
проводниками.
Все вещества проводят электрический ток. Диэлектрики проводят ток в 10151020 раз хуже, чем проводники.
Общая физика. «Электростатика»

3.

ДИЭЛЕКТРИКИ
Кафедра физики
Молекулы диэлектриков могут быть двух видов.
1. У симметричных молекул (H2, O2, N2, CO2) в
отсутствие внешнего электрического поля отсутствует
дипольный момент, такие молекулы называются
неполярными.
Под действием внешнего поля заряды в неполярной
молекуле смещаются относительно друг друга:
положительные по полю, отрицательные против поля.
Молекула приобретает дипольный момент,
пропорциональный напряженности поля. При этом,
положительные и отрицательные заряды, как бы
связаны упругими силами. Неполярная молекула
ведет себя во внешнем поле как упругий диполь.
Общая физика. «Электростатика»
H2

4.

ДИЭЛЕКТРИКИ
Кафедра физики
Молекулы диэлектриков могут быть двух видов.
2. У несимметричных молекул (HCl, H2O, NH, CO) в
отсутствие внешнего электрического поля
присутствует дипольный момент, такие молекулы
HCl
называются полярными.
Действие внешнего поля на полярную молекулу сводится в основном
к стремлению повернуть молекулу так, чтобы ее дипольный момент
установился по направлению поля. На дипольный момент внешнее
поле практически не влияет. Полярная молекула ведет себя во
внешнем поле как жесткий диполь.
Общая физика. «Электростатика»
-

5.

ДИЭЛЕКТРИКИ.
Кафедра физики
СВОЙСТВА И ХАРАКТЕРИСТИКИ
l
p
В диэлектрике смещенные заряды образуют
-q
+q
систему электрических мультиполей,
преимущественно диполей.
Электрический (дипольный) момент p одна из характеристик диполя.
Это вектор, который направлен по оси диполя от отрицательного
заряда к положительному.
Вектор поляризации диэлектрика - это величина, равная отношению
pi молекул, содержащихся в элементе
суммы дипольных моментов всех
V
V
объема
, к объему
pi
i
PE
V
Вектор поляризации - это макроскопическая характеристика, которая
определяется напряженностью поля, вызывающего поляризацию
Общая физика. «Электростатика»

6.

Кафедра физики
ДИЭЛЕКТРИКИ.
СВОЙСТВА И ХАРАКТЕРИСТИКИ
Для линейной изотропной среды связь
соотношением:
PE и
E выражается
PE 0 E E
где E (каппа) – диэлектрическая восприимчивость ( способность
диэлектрика к поляризации).
E связана с диэлектрической проницаемостью вещества
основной макрохарактеристикой диэлектрической поляризации:
E 1
Тогда формулу для
PE можно записать в виде
PE 0 1 E
Общая физика. «Электростатика»
-

7.

ДИЭЛЕКТРИКИ.
Кафедра физики
СВОЙСТВА И ХАРАКТЕРИСТИКИ
Поле внутри диэлектрика
Заряды в диэлектрике и вне его:
- связанные в пределах диэлектрика;
- свободные в пределах диэлектрика
- свободные вне пределов диэлектрика
сторонние заряды
Общее поле в диэлектрике называется микроскопическим или
истинным и определяется суперпозицией полей, созданных
сторонними и связанными
зарядами:
E микро E стор E связ
E микро - зависит от многих факторов, в том числе и от времени.
Более удобно использовать макроскопическое поле E, т.е.
усредненное по бесконечно малому объему значение поля E микро
*
E E микро E стор E связ E0 E
Общая физика. «Электростатика»

8.

Кафедра физики
ДИЭЛЕКТРИКИ.
СВОЙСТВА И ХАРАКТЕРИСТИКИ
Поле внутри диэлектрика
Связанные заряды в диэлектрике могут характеризоваться объемной
*
*
плотностью
и поверхностной плотностью .
*
Поверхностная плотность связана с вектором поляризации
диэлектрика простым соотношением:
*
Pn
P
Pn
- нормальная составляющая вектора поляризации.
В любой точке поверхности поляризованного диэлектрика
поверхностная плотность связанных зарядов равна нормальной
составляющей вектора поляризации в этой точке.
Объемная плотность заряда отлична от нуля в неоднородных
диэлектриках, т.е. в таких диэлектриках, у которых вектор
поляризации имеет различные значения по объему.
Общая физика. «Электростатика»

9.

ДИЭЛЕКТРИКИ.
Кафедра физики
СВОЙСТВА И ХАРАКТЕРИСТИКИ
Пример электрического поля в диэлектрике
*
*
–
+
+
–
+
–
+
–
+
–
–
+
+
–
+
–
+
E0
* +
E
+
–
–
–
Общая физика. «Электростатика»
Две
бесконечные
параллельные
пластины
разноименно заряженные с поверхностной
плотностью
Поле пластин в вакууме имеет напряженность E 0
В поле вносится пластина
изотропного диэлектрика с
проницаемостью
из однородного
диэлектрической
Под действием поля диэлектрик поляризуется, на
его поверхности появятся связанные
заряды с
поверхностной плотностью
Эти заряды создадут внутри * пластины
однородное поле с напряженностью E
*
Поле E направлено навстречу полю E 0

10.

Кафедра физики
ДИЭЛЕКТРИКИ.
Пример электрического поля в диэлектрике
*
Две области пространства между пластинами:
1. Поле вне диэлектрика с напряженностью E 0;
2. Поле в диэлектрике
с напряженностью
*
–
+
–
+
–
+
+
+
E E0 E ,
–
или в скалярной форме
–
+
–
+
–
E0
* +
E
+
E
–
Поле в диэлектрике связано с внешним полем
соотношением
E E0
–
–
E E0 E *
Таким образом, поле в диэлектрике
оказывается меньше поля вне диэлектрика.
–
+
+
*
Диэлектрическая проницаемость показывает, во
сколько раз ослабляется электрическое поле в
диэлектрике.
Общая физика. «Электростатика»

11.

Кафедра физики
ДИЭЛЕКТРИКИ.
Теорема Гаусса при наличии диэлектриков.
Вектор электрического смещения.
Связанные заряды появляются в диэлектрике под действием поля
сторонних зарядов. На электрическое поле сторонних зарядов
накладывается поле связанных зарядов.
Результирующее поле характеризуется вектором
зависит от свойств диэлектрической среды.
E , который
Эта зависимость определяется относительной диэлектрической
проницаемостью вещества и учитывается в теореме Гаусса:
S
q
E , dS
0
Формула малопригодна для нахождения Е, т.к.
справа q является суммой сторонних и связанных
зарядов, которые в свою очередь определяются
величиной неизвестной Е.
Общая физика. «Электростатика»

12.

Кафедра физики
ДИЭЛЕКТРИКИ.
Теорема Гаусса при наличии диэлектриков.
Вектор электрического смещения (индукции).
Новая векторная характеристика электрического поля - вектор
электрического смещения (электрической индукции) D , не
зависит от свойств среды.
Для линейного изотропного диэлектрика связь между векторами
выражается соотношением:
D ε0 E P
P ε0 χE
D ε0 E 0 E
D 0 E
В вакууме
1 , следовательно
Общая физика. «Электростатика»
D 0 E
Eи D

13.

Кафедра физики
ДИЭЛЕКТРИКИ.
Вектор электрического смещения.
*
+
*
–
+
–
+
–
+
–
+
–
+
+
E0
Электрическое смещение внешнего поля равно D0
Для определения D умножим уравнение для
электрического поля в диэлектрике E E 0 на 0
0 E0
0 E
0 E0
–
+
+
Вычислим значение D между заряженными пластинами
– +
E*
–
+
E
–
–
–
Получили равенство
D D0 .
Вывод:
Электрическое смещение внутри диэлектрика
совпадает с электрическим смещением внешнего поля
Теорема
Гаусса:
с
учетом
введенной
характеристики поля может быть записана в виде:
Общая физика. «Электростатика»
S
D , dS q

14.

ДИЭЛЕКТРИКИ.
Кафедра физики
Постулат Максвелла.
Теорема Гаусса применима для расчета полей, созданных свободными
(сторонними) зарядами и не может быть использована для расчета
полей в неоднородных средах. Теорема не учитывает объемных
поляризационных зарядов и их влияние на поле свободных зарядов.
Задача: найти метод учета всех возникающих при поляризации
связанных поляризационных зарядов.
Рассмотрим неоднородную диэлектрическую
имеются свободные (сторонние) заряды
среду,
в
которой
Поле сторонних зарядов поляризует среду, возникают связанные
заряды с распределением, зависящим от свойств диэлектрика.
Созданную систему зарядов перенесем без изменения их распределения
в однородную среду (например, в вакуум) с 1
Общая физика. «Электростатика»

15.

ДИЭЛЕКТРИКИ.
Кафедра физики
Постулат Максвелла.
Для анализа поля, созданного получившейся системой зарядов, теперь
можно применить теорему Гаусса.
S
q q*
E , dS
0
*
q
В формуле разделены сторонние заряды q и связанные заряды .
Величина стороннего заряда
q известна или может быть задана
*
q
Нужно выразить заряд
через обобщенные параметры поля, тогда
можно получить уравнение Гаусса в более общем виде.
Рассмотрим в системе перенесенных из диэлектрика в вакуум
зарядов произвольный объем V с поверхностью S.
*
*
q
q
В объеме будут и поверхностные S и объемные V связанные заряды
Общая физика. «Электростатика»

16.

Кафедра физики
ДИЭЛЕКТРИКИ.
Постулат Максвелла.
До поляризации объем был электрически нейтрален, нейтральным
*
*
q
q
он должен остаться и после поляризации:
S
V
Каждый из зарядов выразим в интегральной форме через плотности
qV* g*dV .
qS dS ,
*
*
В итоге получим:
V
S
*
*
dS
dV
q
S
V
Поскольку Pn , dS P dS P , dS .
n
E
Заменим выражение под первым
*
интегралом, получим:
PE , dS q dV
*
*
S
Общая физика. «Электростатика»
V

17.

Кафедра физики
ДИЭЛЕКТРИКИ.
Постулат Максвелла.
Вернемся к теореме Гаусса
S
и преобразуем ее
q q*
E , dS
0
q q* q q* q 1
*
E
,
d
S
q dV
S
0
0 0 0 0 V
*
С учетом полученного выше равенства
P
,
d
S
E
q dV
S
запишем:
S
q 1
q 1
*
E , dS q dV
0 0 V
0 0
V
S
Получили два интеграла по поверхности. Объединим их
Общая физика. «Электростатика»
PE , dS

18.

Кафедра физики
ДИЭЛЕКТРИКИ.
Постулат Максвелла.
S
q 1
E , dS
0 0
PE , dS
S
S
1
E , dS
0
S
q
PE , dS
0
Учитывая, что сумма интегралов равна интегралу суммы, получим:
0 E PE , dS q
Соотношение 0 E PE D - это вектор смещения, записанный
S
в общем виде для диэлектрических сред с различными свойствами
С учетом выражения для
D
в окончательном виде получим:
D, dS q
S
Общая физика. «Электростатика»

19.

ДИЭЛЕКТРИКИ.
Кафедра физики
Постулат Максвелла.
D, dS q
Это соотношение называют постулатом
Максвелла
S
Поток вектора смещения через замкнутую поверхность в
произвольной среде равен стороннему заряду, заключенному
внутри поверхности.
Теорема Гаусса выступает как частный случай постулата Максвелла
В дифференциальной форме (вывод совпадает с проведенным ранее
для теоремы Гаусса) постулат Максвелла выглядит так:
div D q
q - объемная плотность свободного заряда
Постулат Максвелла выражает закон создания электрических
полей действием зарядов в произвольных средах
Общая физика. «Электростатика»

20.

E
2D
2
Кафедра физики
ДИЭЛЕКТРИКИ.
Условия на границе двух диэлектриков
При переходе электрического поля через границу раздела двух
диэлектрических сред вектор напряженности и вектор смещения
скачкообразно меняются по величине и напряжению. Соотношения,
характеризующие эти изменения, называют граничными условиями. Таких
условий четыре.
Рассмотрим границу между двумя диэлектриками с проницаемостями 1 и 2
E1
D1
1
ε1
ε1
ε2 1
2
ε2 1
Общая физика. «Электростатика»
1
2
Пусть в диэлектриках
создано поле: с
напряженностью E 1 и
электрическим
смещением D1 в
первом
диэлектрике, и
и 2 …..во
E 2… D
втором.

21.

2D
E
n
2E
D
2
n
2
Кафедра физики
ДИЭЛЕКТРИКИ.
Условия на границе двух диэлектриков
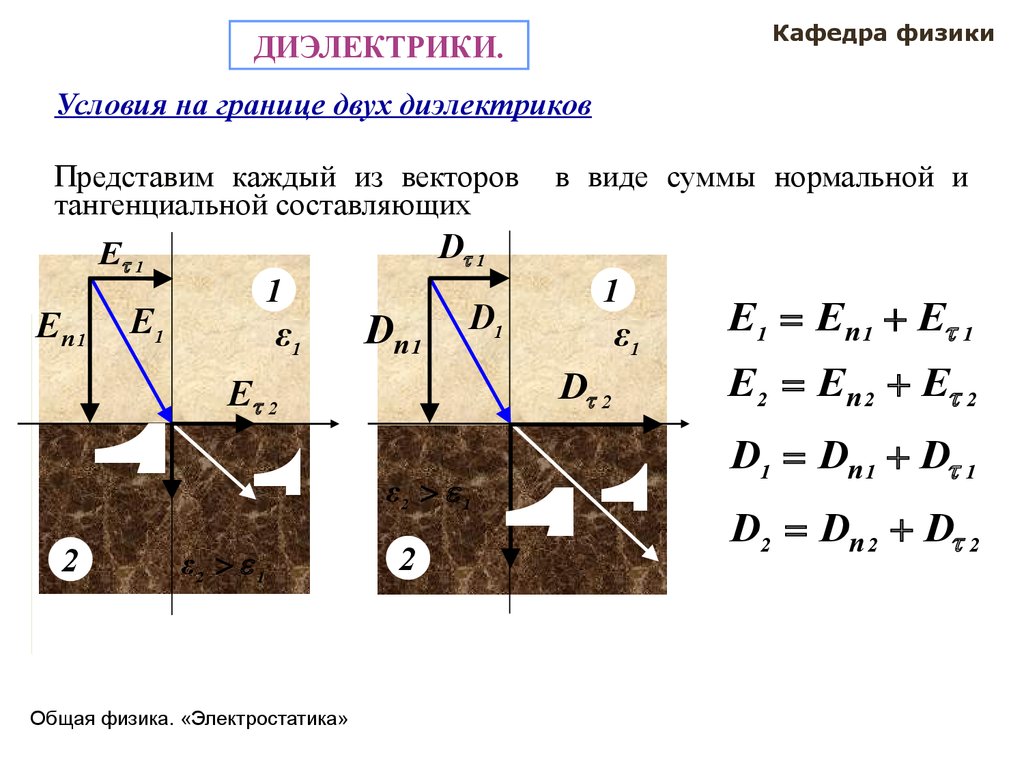
Представим каждый из векторов
тангенциальной составляющих
E 1
En1
1
E1
ε1
D 1
Dn 1
D1
ε2 1
ε2 1
Общая физика. «Электростатика»
1
ε1
D 2
E 2
2
в виде суммы нормальной и
2
E 1 E n 1 E 1
E 2 E n 2 E 2
D1 Dn 1 D 1
D2 Dn 2 D 2

22.

2D
E
n
2E
D
2
n
2
Кафедра физики
ДИЭЛЕКТРИКИ.
Условия на границе двух диэлектриков
D 1
E 1
E n1
1
E1
ε1
Dn 1
D1
ε2 1
ε2 1
ε1
D 2
E 2
2
1
2
Если
применить
постулат
Максвелла
к
замкнутой
поверхности контура, который
частично проходит в первом
диэлектрике, частично во втором,
охватывая
границу
раздела
диэлектриков, можно получить
следующие условия на границе:
1. Dn 1 Dn 2 . Это условие непрерывности нормальных
составляющих вектора смещения на границе раздела двух сред
Используя формулу D 0 E , запишем соотношение для нормальных
составляющих вектора напряженности поля – второе граничное условие:
Общая физика. «Электростатика»

23.

2D
E
n
2E
D
n
22
Кафедра физики
ДИЭЛЕКТРИКИ.
Условия на границе двух диэлектриков
En1
1
E1
ε1
Dn 1
D1
ε2 1
ε2 1
1
ε1
D 2
E 2
2
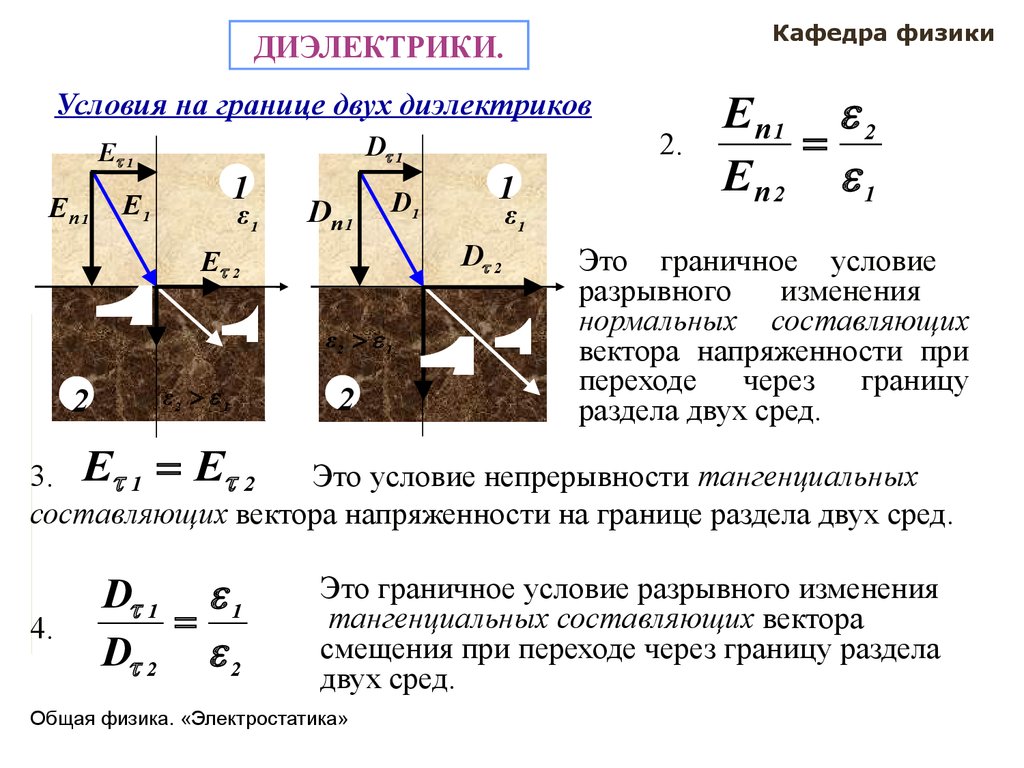
2.
D 1
E 1
2
En1 2
En2 1
Это граничное условие
разрывного
изменения
нормальных составляющих
вектора напряженности при
переходе через границу
раздела двух сред.
3. E 1 E 2
Это условие непрерывности тангенциальных
составляющих вектора напряженности на границе раздела двух сред.
4.
D 1 1
D 2 2
Это граничное условие разрывного изменения
тангенциальных составляющих вектора
смещения при переходе через границу раздела
двух сред.
Общая физика. «Электростатика»

24.

2D
E
n
2E
D
n
22
Кафедра физики
ДИЭЛЕКТРИКИ.
Условия на границе двух диэлектриков
D 1
E 1
En1
1
E1
ε1
Dn 1
D1
1
ε1
D 2
E 2
ε2 1
2
ε2 1
2
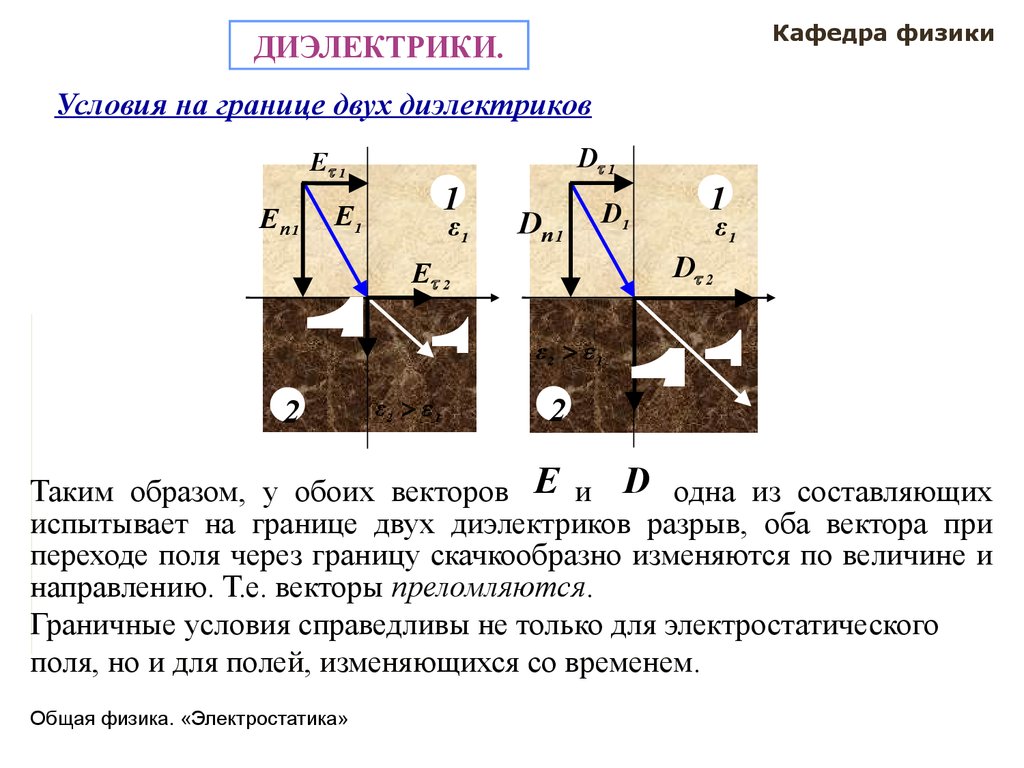
Таким образом, у обоих векторов E и D одна из составляющих
испытывает на границе двух диэлектриков разрыв, оба вектора при
переходе поля через границу скачкообразно изменяются по величине и
направлению. Т.е. векторы преломляются.
Граничные условия справедливы не только для электростатического
поля, но и для полей, изменяющихся со временем.
Общая физика. «Электростатика»