Понятие о чистом изгибе

1. И б з г и

2. Понятие о чистом изгибе

• Чистым изгибом называется такой вид
деформации, при котором в любом поперечном
сечении бруса возникает только изгибающий
момент.
• Деформация чистого изгиба будет иметь место,
если к прямому брусу в плоскости, проходящей
через ось, приложить две равные по величине и
противоположные по знаку пары сил.
• На изгиб работают балки, оси, валы и другие
детали конструкций.
• При изучении деформации изгиба будем
мысленно представлять себе, что балка состоит
из бесчисленного количества волокон,
параллельных оси.

3.

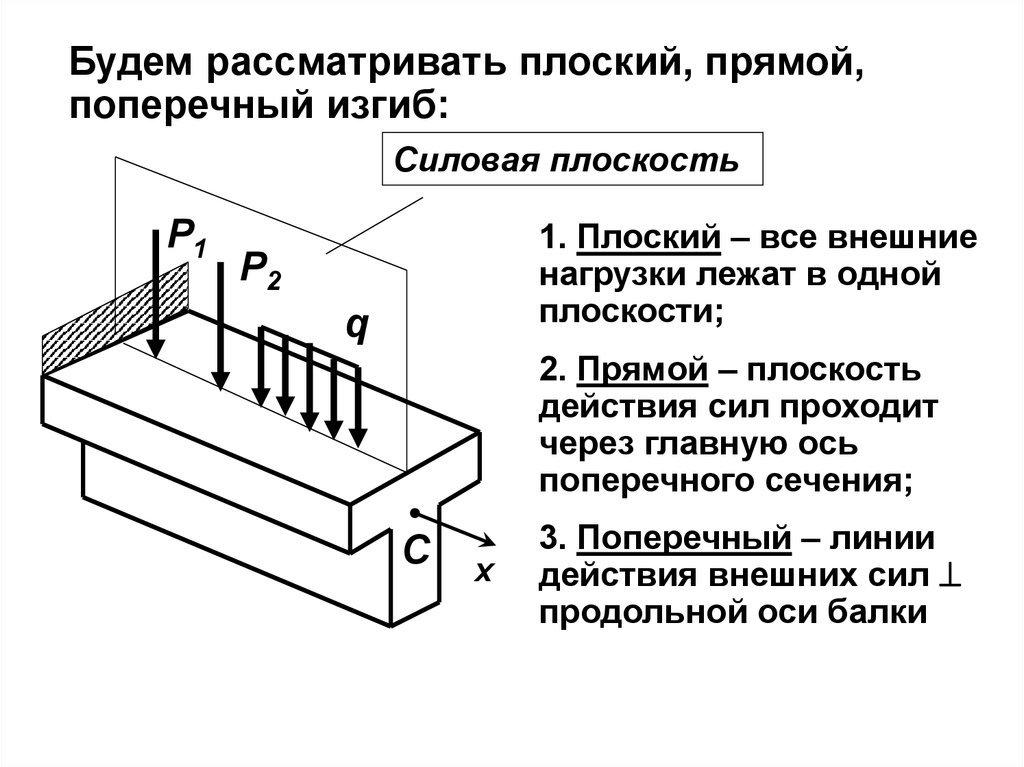
Будем рассматривать плоский, прямой,
поперечный изгиб:
Силовая плоскость
Р1
1. Плоский – все внешние
нагрузки лежат в одной
плоскости;
Р2
q
2. Прямой – плоскость
действия сил проходит
через главную ось
поперечного сечения;
C
x
3. Поперечный – линии
действия внешних сил
продольной оси балки

4.

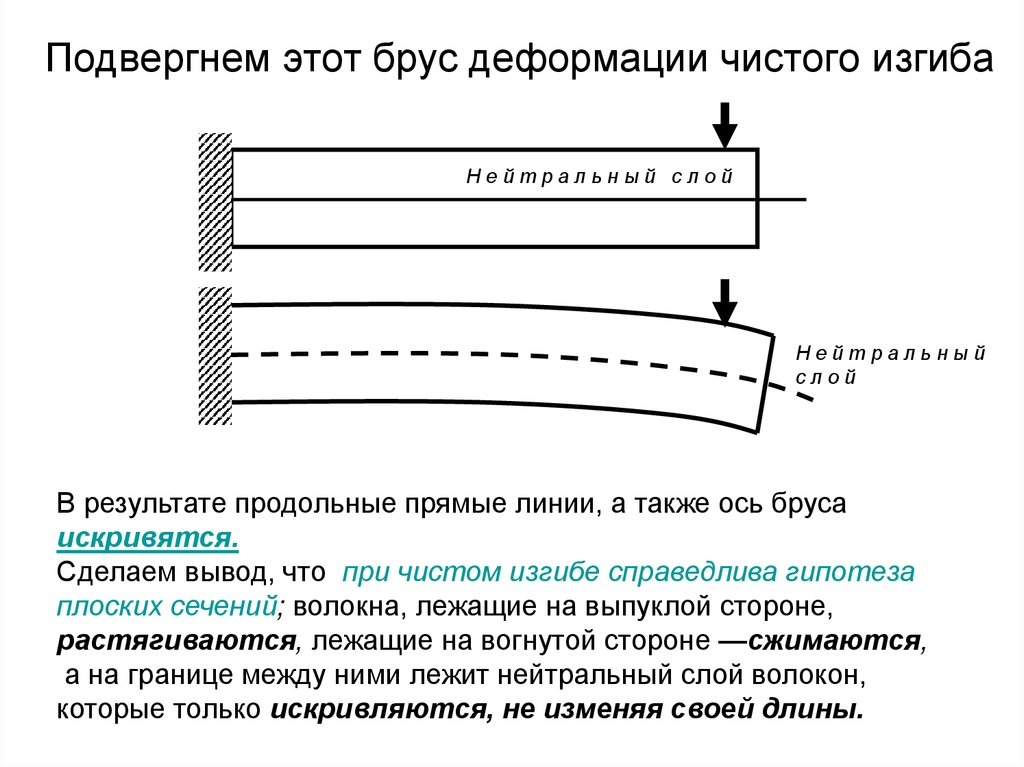
Подвергнем этот брус деформации чистого изгиба
Нейтральный слой
Нейтральный
слой
В результате продольные прямые линии, а также ось бруса
искривятся.
Сделаем вывод, что при чистом изгибе справедлива гипотеза
плоских сечений; волокна, лежащие на выпуклой стороне,
растягиваются, лежащие на вогнутой стороне —сжимаются,
а на границе между ними лежит нейтральный слой волокон,
которые только искривляются, не изменяя своей длины.

5. Изгибающий момент и поперечная сила.

Из теоретической механики известно, что
опорные реакции балок определяют,
составляя для всей балки и решая уравнения
равновесия статики.
При определении внутренних сил, реакции
связей учитываются наравне с активными
внешними силами, действующими на балку.
Для определения внутренних силовых
факторов применяют метод сечений, причем
изображают балку только одной линией —
осью, к которой приложены активные и
реактивные силы.

6.

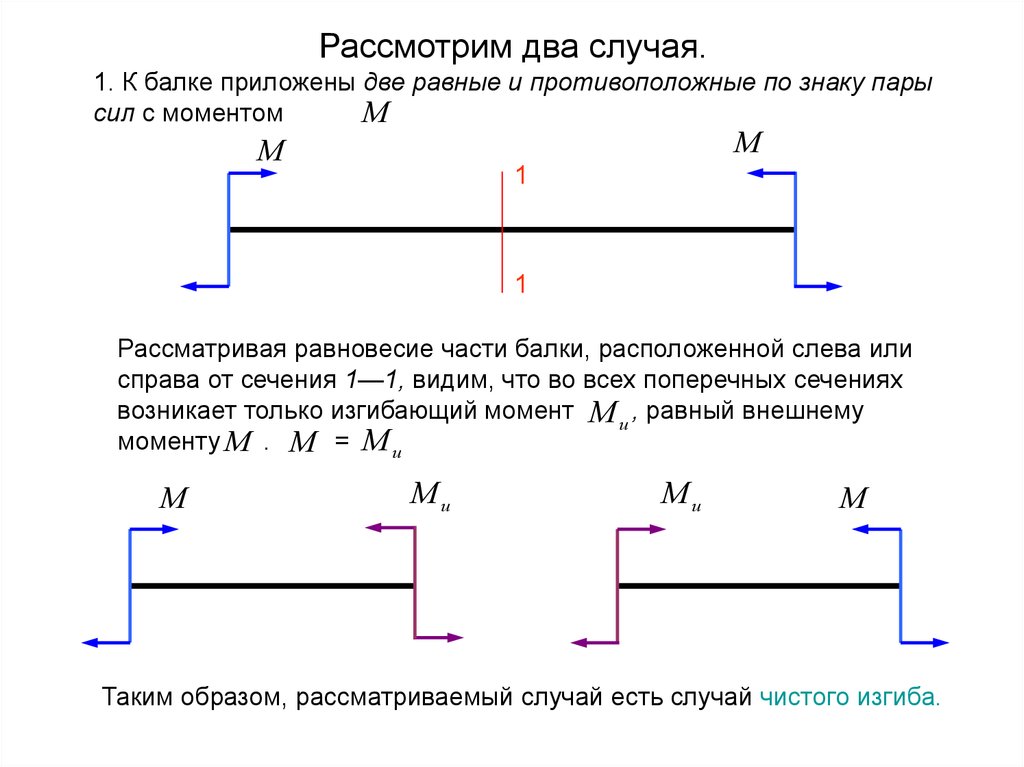
Рассмотрим два случая.
1. К балке приложены две равные и противоположные по знаку пары
сил с моментом
М
М
М
1
1
Рассматривая равновесие части балки, расположенной слева или
справа от сечения 1—1, видим, что во всех поперечных сечениях
возникает только изгибающий момент М и , равный внешнему
моменту М . М = М и
М
Ми
Ми
М
Таким образом, рассматриваемый случай есть случай чистого изгиба.

7.

Изгибающий момент есть результирующий момент
относительно нейтральной оси внутренних
нормальных сил, действующих в поперечном сечении
балки.
Обратим внимание на то, что изгибающий момент
имеет разное направление для левой и правой частей
балки.
Это говорит о непригодности правила
знаков статики при определении знака
изгибающего момента.

8.

F
RA
RB
x
RA
Ми
x
Q
Ми
F
RB
Q
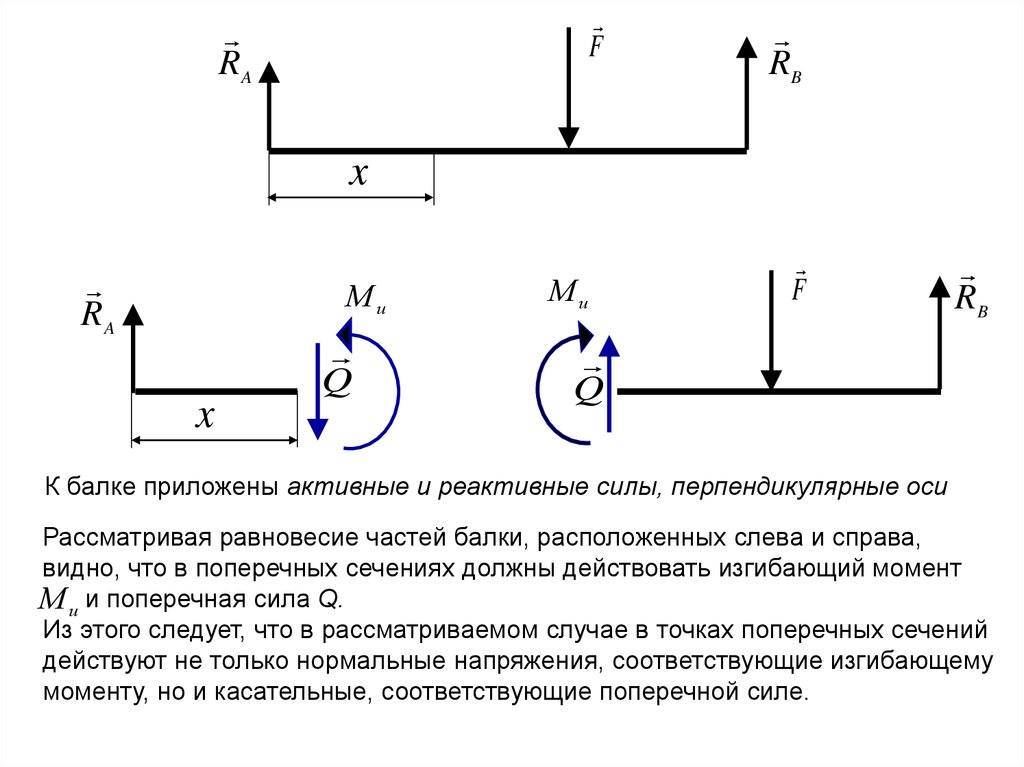
К балке приложены активные и реактивные силы, перпендикулярные оси
Рассматривая равновесие частей балки, расположенных слева и справа,
видно, что в поперечных сечениях должны действовать изгибающий момент
М и и поперечная сила Q.
Из этого следует, что в рассматриваемом случае в точках поперечных сечений
действуют не только нормальные напряжения, соответствующие изгибающему
моменту, но и касательные, соответствующие поперечной силе.

9.

F
RA
RB
x
RA
Ми
x
Q
Ми
F
RB
Q
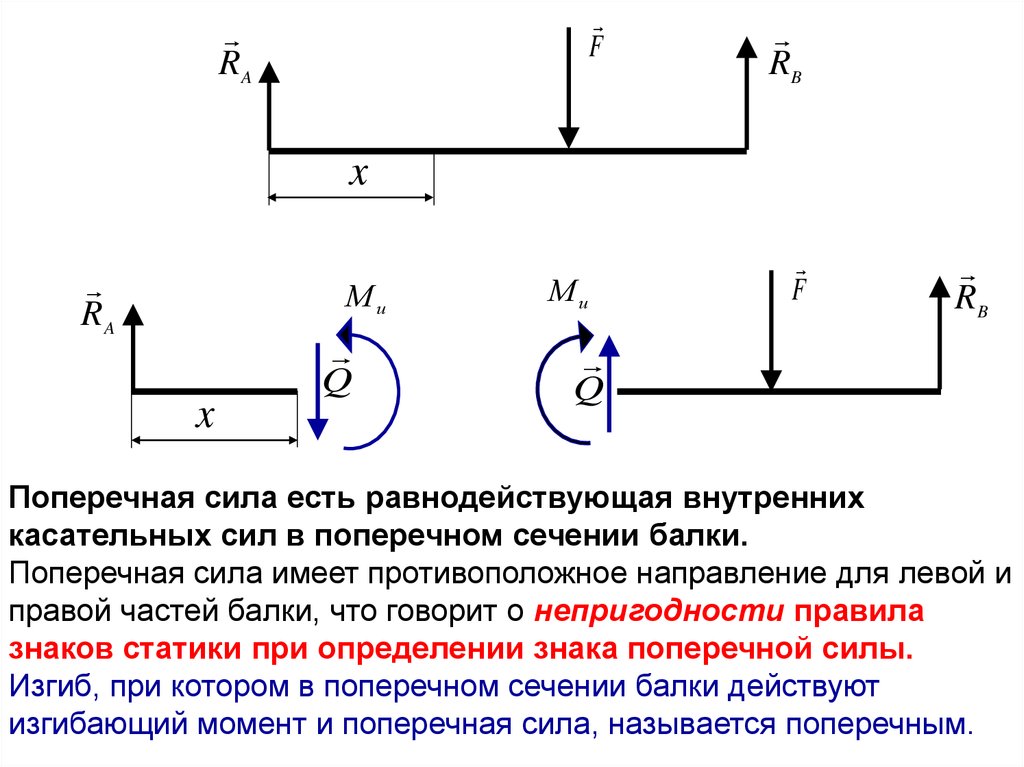
Поперечная сила есть равнодействующая внутренних
касательных сил в поперечном сечении балки.
Поперечная сила имеет противоположное направление для левой и
правой частей балки, что говорит о непригодности правила
знаков статики при определении знака поперечной силы.
Изгиб, при котором в поперечном сечении балки действуют
изгибающий момент и поперечная сила, называется поперечным.

10.

F
RA
RB
x
RA
Ми
x
Q
Ми
F
RB
Q
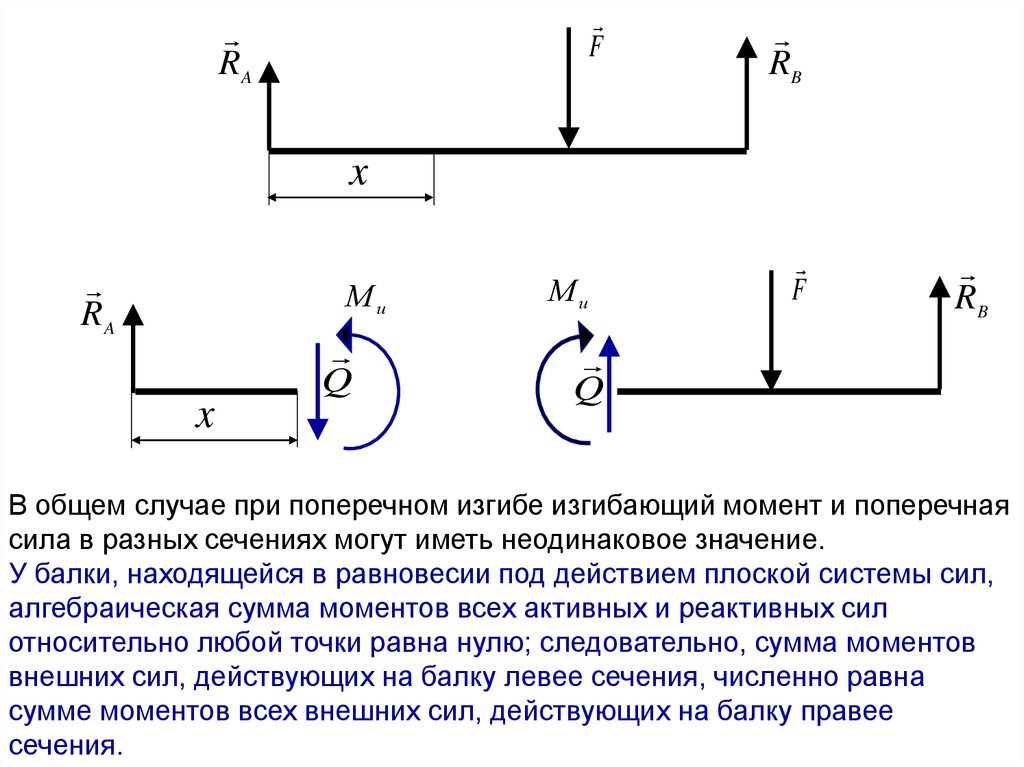
В общем случае при поперечном изгибе изгибающий момент и поперечная
сила в разных сечениях могут иметь неодинаковое значение.
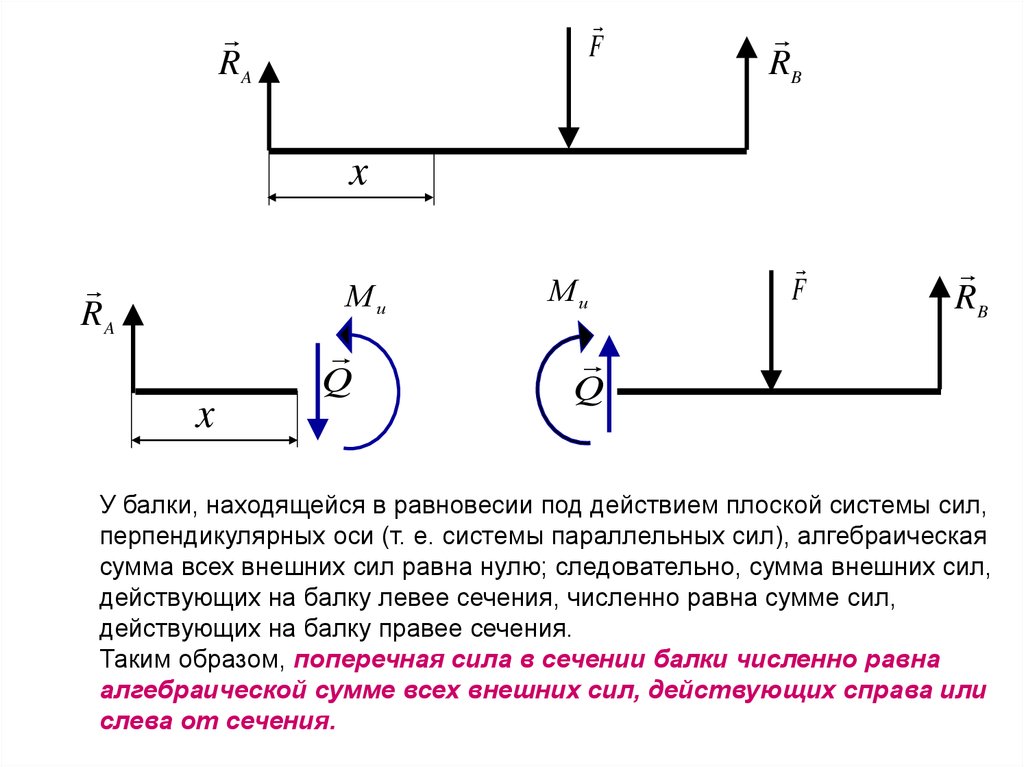
У балки, находящейся в равновесии под действием плоской системы сил,
алгебраическая сумма моментов всех активных и реактивных сил
относительно любой точки равна нулю; следовательно, сумма моментов
внешних сил, действующих на балку левее сечения, численно равна
сумме моментов всех внешних сил, действующих на балку правее
сечения.

11.

F
RA
RB
x
RA
Ми
x
Q
Ми
F
Q
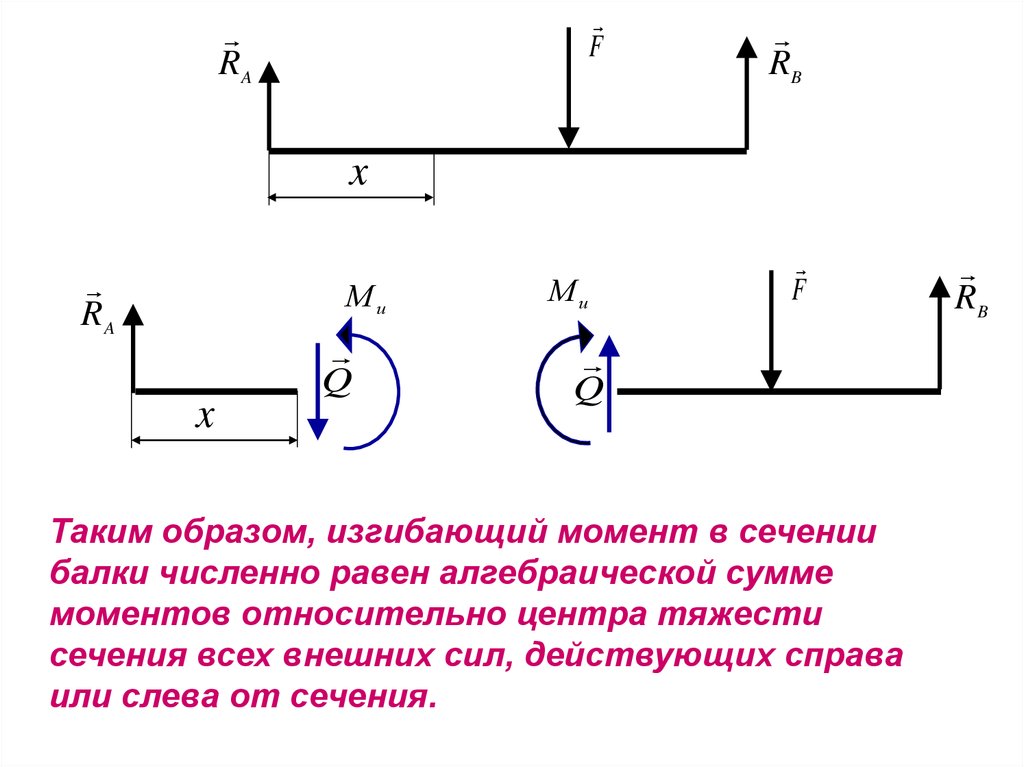
Таким образом, изгибающий момент в сечении
балки численно равен алгебраической сумме
моментов относительно центра тяжести
сечения всех внешних сил, действующих справа
или слева от сечения.
RB

12.

F
RA
RB
x
RA
Ми
x
Q
Ми
F
RB
Q
У балки, находящейся в равновесии под действием плоской системы сил,
перпендикулярных оси (т. е. системы параллельных сил), алгебраическая
сумма всех внешних сил равна нулю; следовательно, сумма внешних сил,
действующих на балку левее сечения, численно равна сумме сил,
действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна
алгебраической сумме всех внешних сил, действующих справа или
слева от сечения.

13.

Ми
Ми
Ми
Ми
+
-
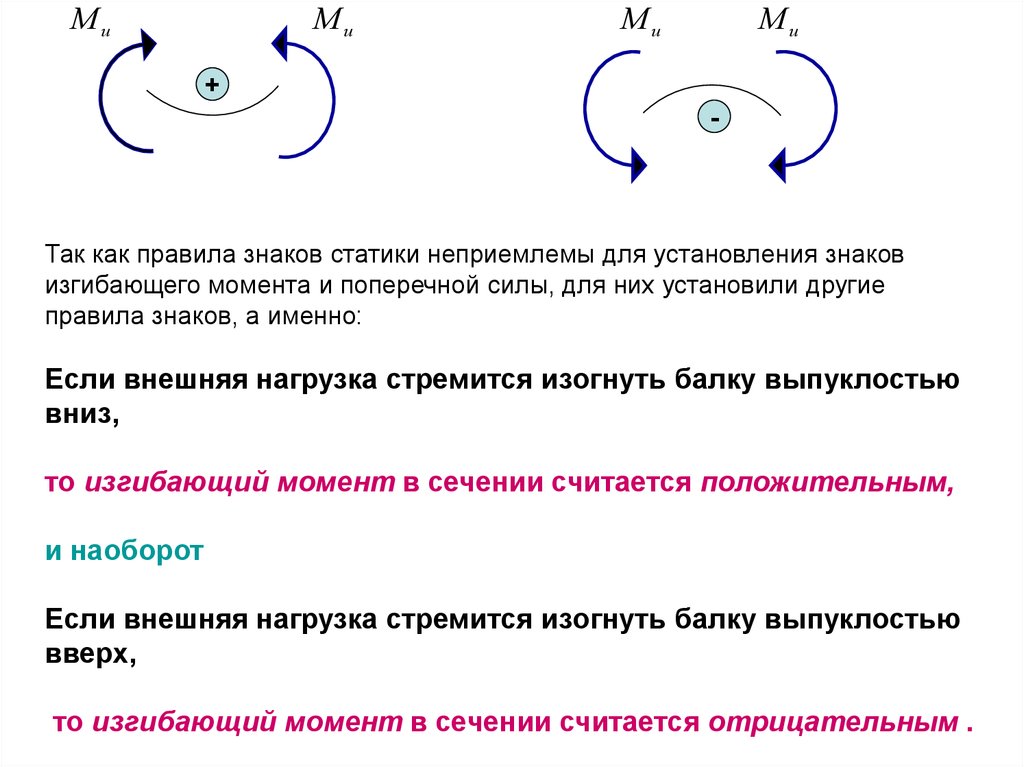
Так как правила знаков статики неприемлемы для установления знаков
изгибающего момента и поперечной силы, для них установили другие
правила знаков, а именно:
Если внешняя нагрузка стремится изогнуть балку выпуклостью
вниз,
то изгибающий момент в сечении считается положительным,
и наоборот
Если внешняя нагрузка стремится изогнуть балку выпуклостью
вверх,
то изгибающий момент в сечении считается отрицательным .

14.

Q
+
Q
+
Q
-
-
Q
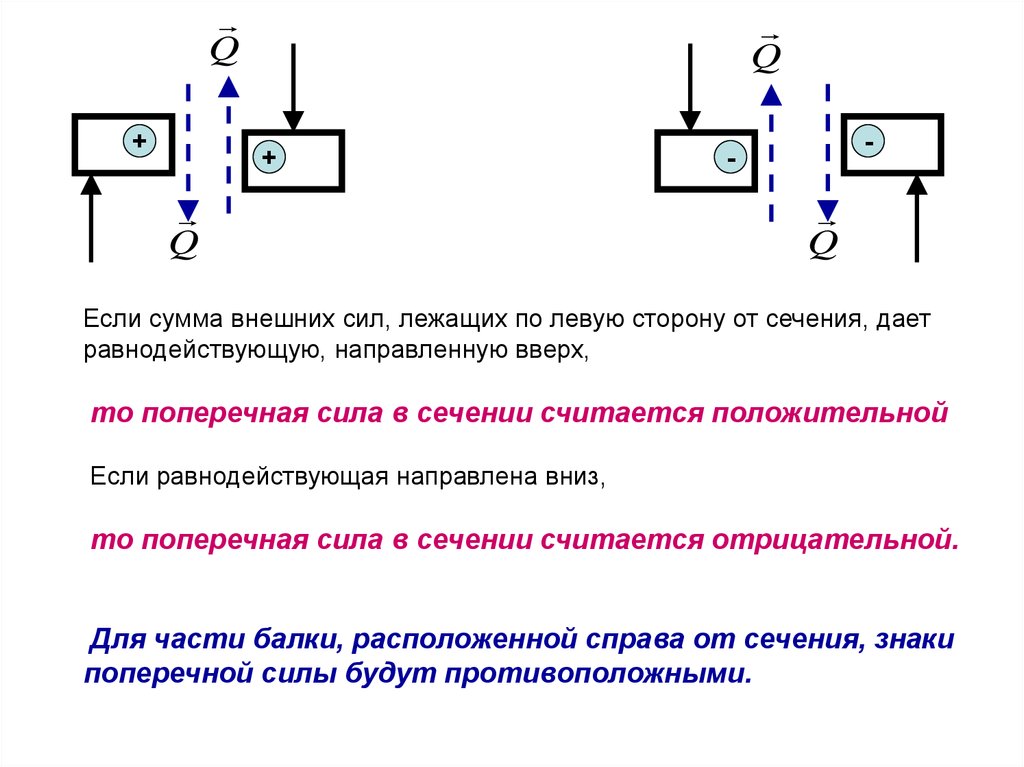
Если сумма внешних сил, лежащих по левую сторону от сечения, дает
равнодействующую, направленную вверх,
то поперечная сила в сечении считается положительной
Если равнодействующая направлена вниз,
то поперечная сила в сечении считается отрицательной.
Для части балки, расположенной справа от сечения, знаки
поперечной силы будут противоположными.

15.

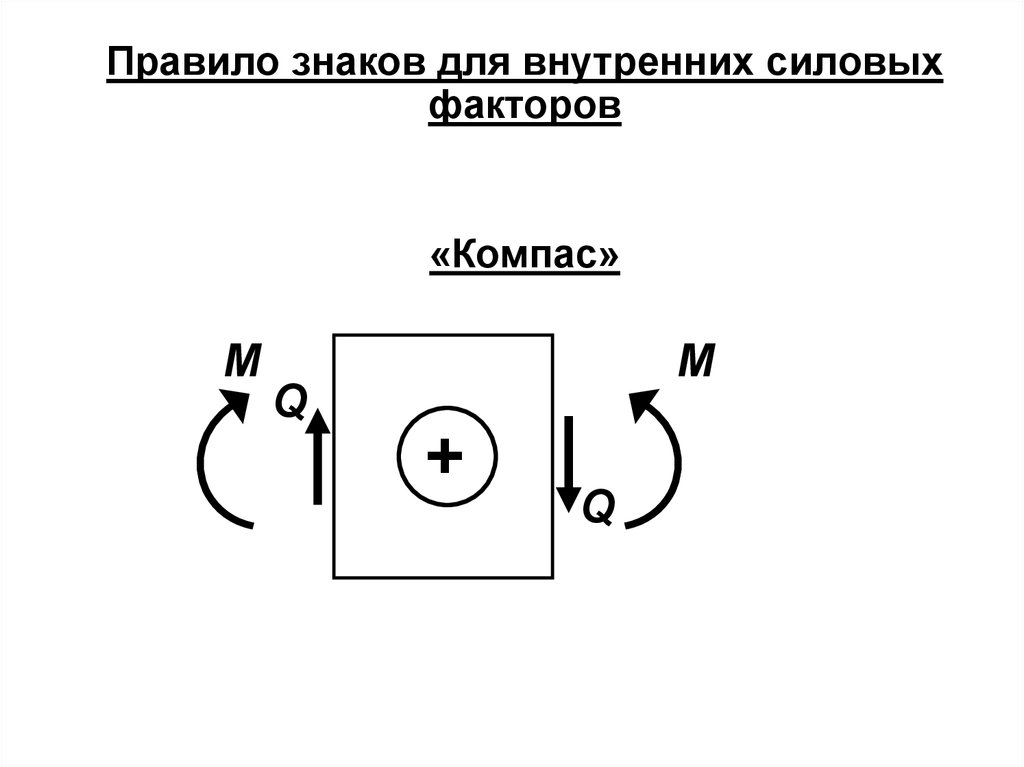
Правило знаков для внутренних силовых
факторов
«Компас»
M
M
Q
+
Q

16.

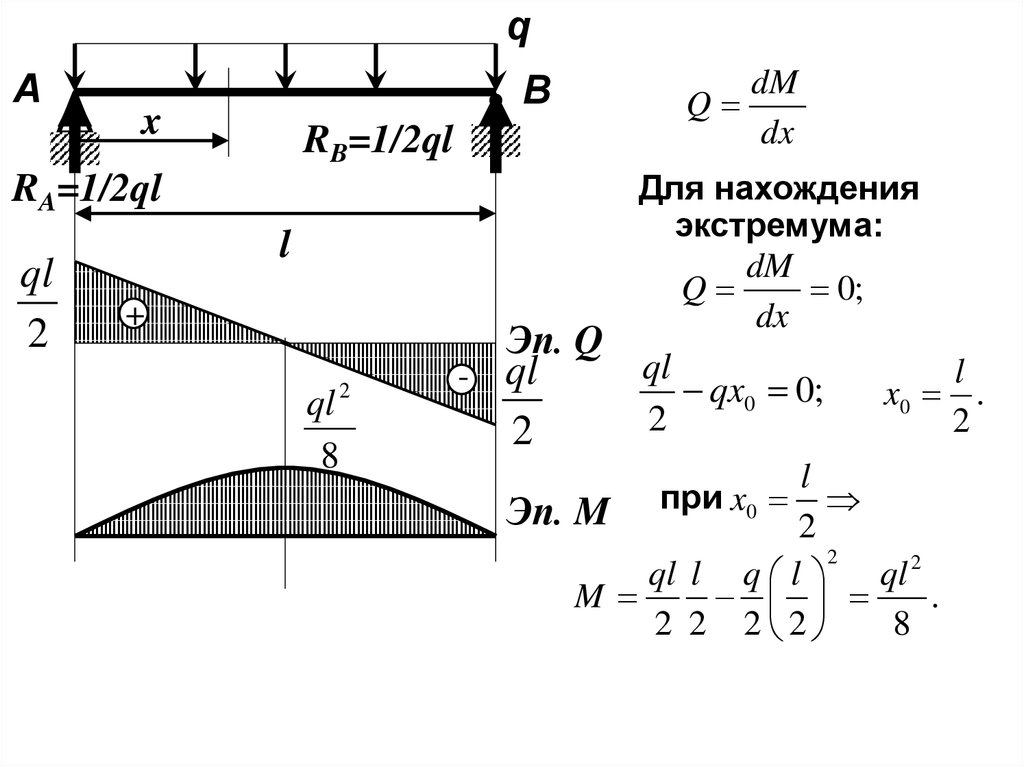
Построение эпюр М и Q
Рассмотрим простой пример:
q
A
B
x
RB=1/2ql
RA=1/2ql
l
1. Определить
реакции опор
2. Разбить балку на
характерные участки
3. Воспольз. методом
сечений
Эп. Q
Эп. M

17.

3. Воспользуемся методом сечений:
q
y
A
RA
c
x
M
Fy 0;
RA qx Q 0
0 x l
Q RA qx;
x
Q
ql
при x 0, Q R A
2
ql
ql
при x l , Q
ql .
2
2
2
qx
M C 0; RA x 2 2M 0
qx
M RA x
; 0 x l
2
при
x 0, M 0;
при
x l,
2
ql
ql
M l
0;
2
2

18.

q
A
B
x
RB=1/2ql
RA=1/2ql
ql
2
l
+
Эп. Q
ql
8
2
-
ql
2
dM
Q
dx
Для нахождения
экстремума:
dM
Q
0;
dx
ql
qx0 0;
2
l
x0 .
2
l
Эп. M при x0 2
2
ql l q l
ql 2
M
.
2 2 2 2
8

19.

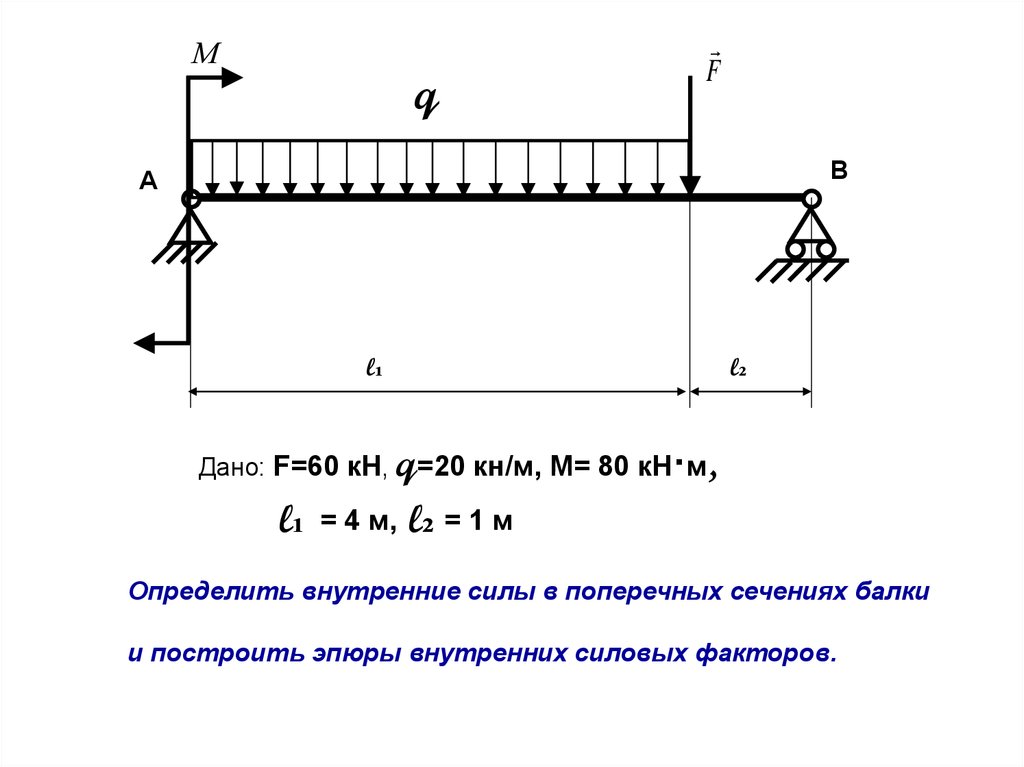
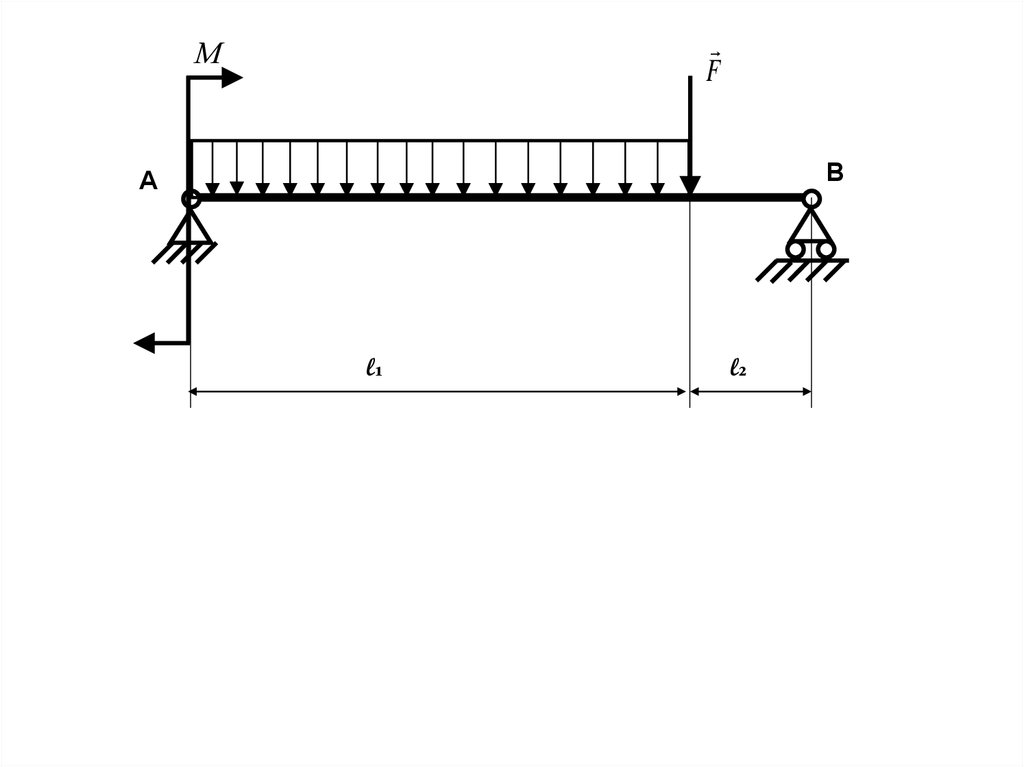
М
q
F
В
А
l₁
l₂
Дано: F=60 кН, q=20 кн/м, М= 80 кН·м,
l₁
= 4 м,
l₂ = 1 м
Определить внутренние силы в поперечных сечениях балки
и построить эпюры внутренних силовых факторов.

20.

Используя принцип освобождаемости от связей
представляем тело свободным и вместо связей
указываем реакции в точках А и В.
Определяем реакции связей (опорные реакции).

21.

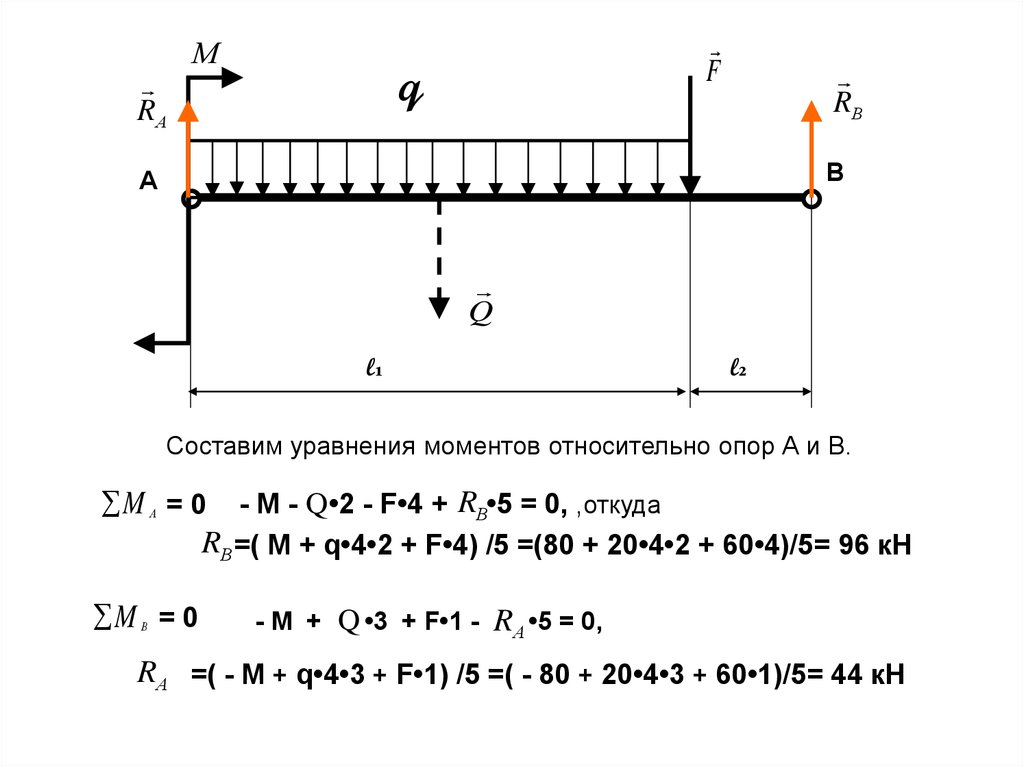
RА
М
F
q
RВ
В
А
Q
l₁
l₂
Составим уравнения моментов относительно опор А и В.
M = 0 - М - Q•2 - F•4 + RВ•5 = 0, ,откуда
RВ =( М + q•4•2 + F•4) /5 =(80 + 20•4•2 + 60•4)/5= 96 кН
А
M = 0
В
- М + Q •3 + F•1 -
RА •5 = 0,
RА =( - М + q•4•3 + F•1) /5 =( - 80 + 20•4•3 + 60•1)/5= 44 кН

22.

Проверим правильность определения реакций, составив уравнение
проекций на ось у:
Y =0
RА + RВ - 4•q - F = 44 + 96 – 80 – 60 = 0
Полученное тождество 0 = 0 говорит о том, что реакции определены правильно.
Разобьем балку на грузовые участки и применим метод сечений.
Напомним, что в общем случае границами участков балки являются концы
балки, опоры, начало и конец распределенной нагрузки, точки приложения
сосредоточенных сил и внешних моментов.

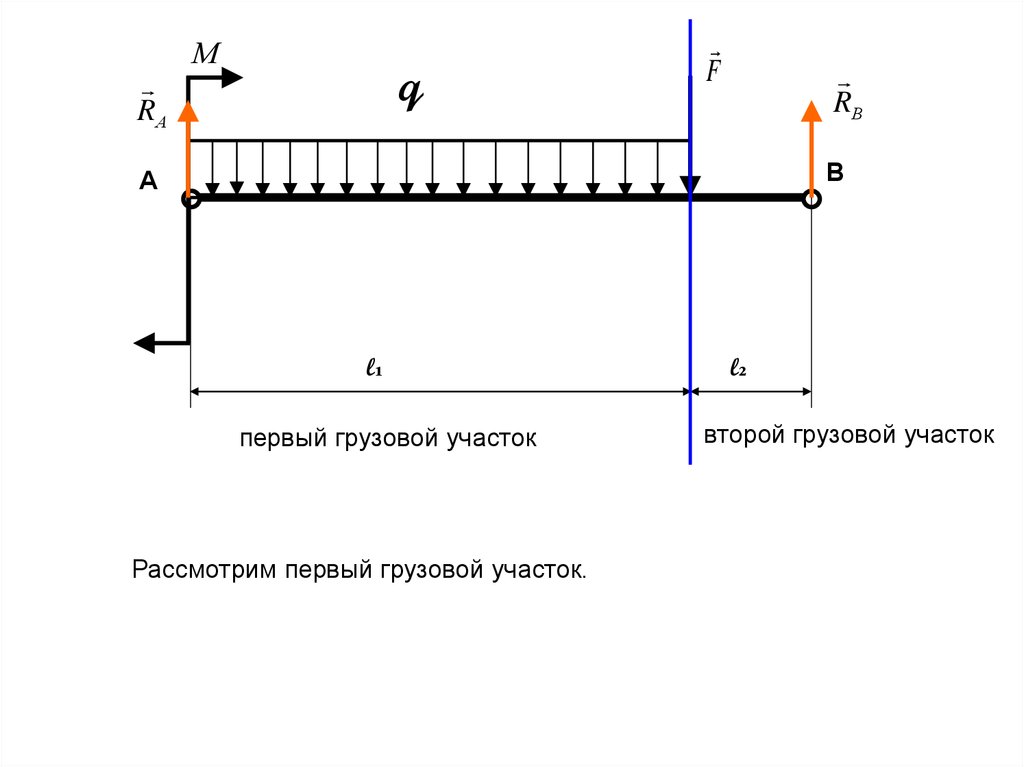
23.

RА
М
q
F
RВ
В
А
l₁
первый грузовой участок
Рассмотрим первый грузовой участок.
l₂
второй грузовой участок

24.

RА
М
q
1
x
А
Х
1
l₁
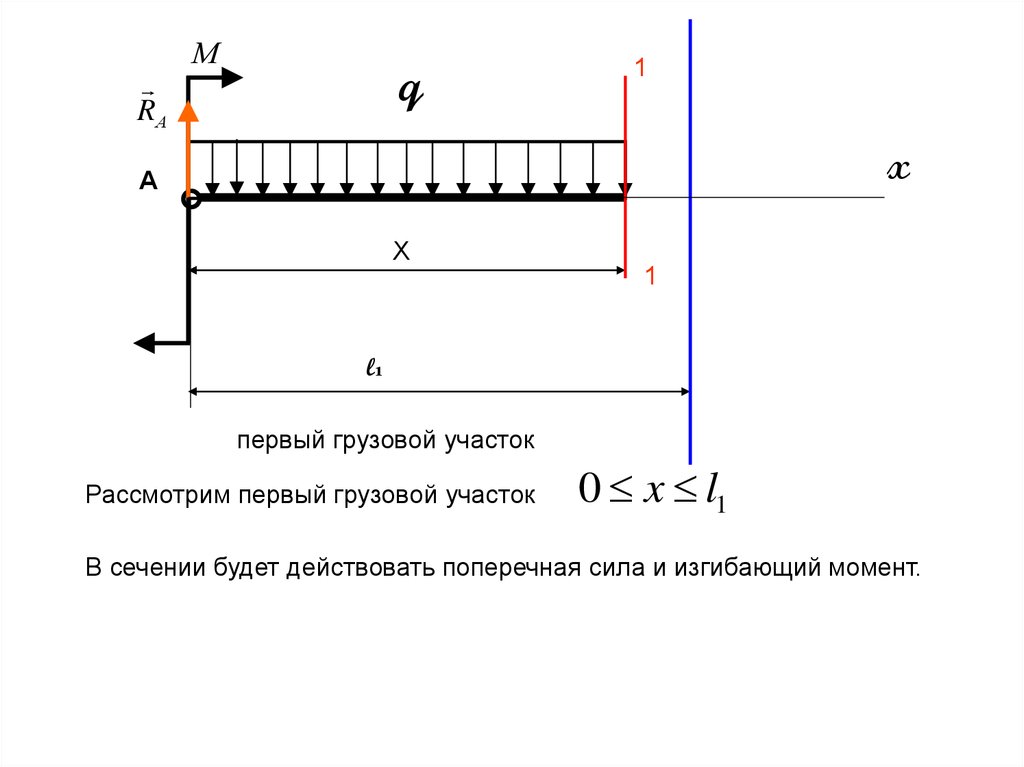
первый грузовой участок
Рассмотрим первый грузовой участок
0 x l1
В сечении будет действовать поперечная сила и изгибающий момент.

25.

RА
М
q
1
А
С
x
Х
0 Х 4 м
l₁
1
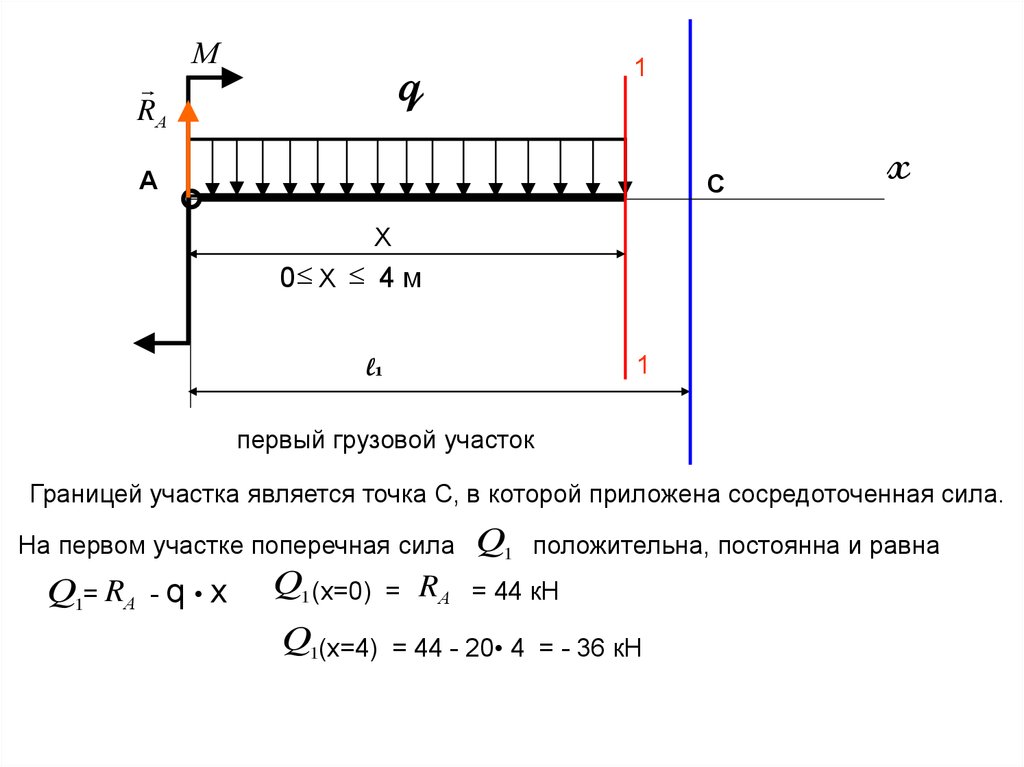
первый грузовой участок
Границей участка является точка С, в которой приложена сосредоточенная сила.
На первом участке поперечная сила
Q1= RА - q • x
Q1 (x=0)
Q1(x=4)
=
Q1
положительна, постоянна и равна
RА = 44 кН
= 44 - 20• 4 = - 36 кН

26.

RА
1
М
q
А
С
Х
0 Х 4 м
l₁
1
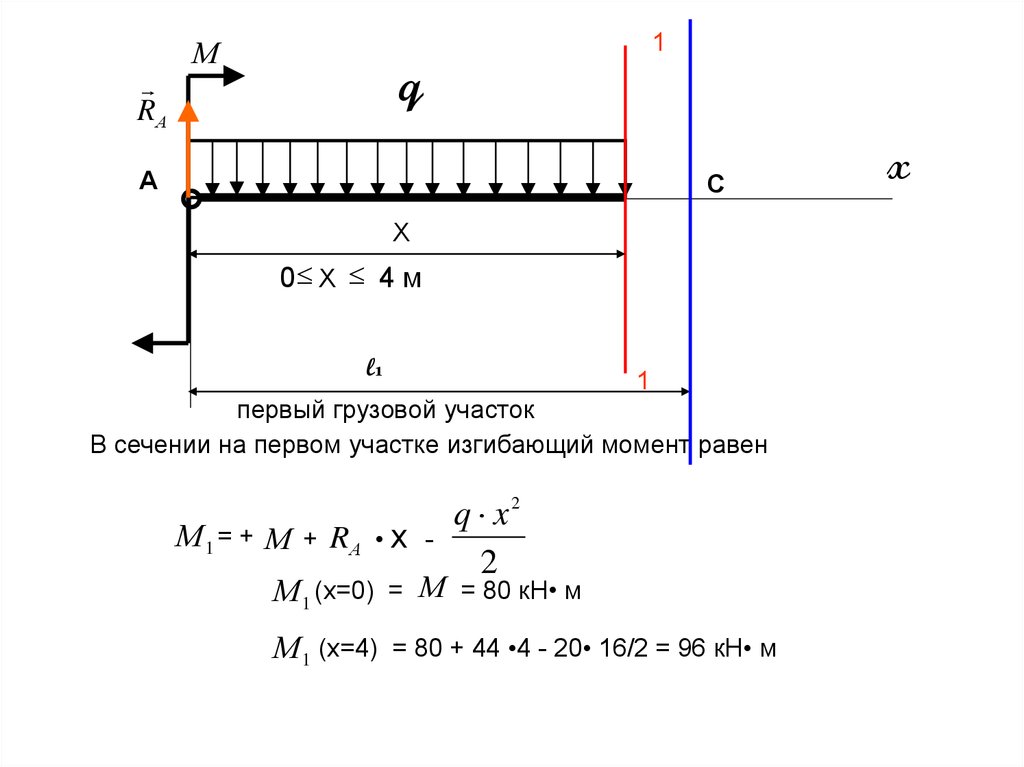
первый грузовой участок
В сечении на первом участке изгибающий момент равен
М 1 = + М + RА • x -
q x2
2
М 1 (x=0) = М = 80 кН• м
М 1 (x=4) = 80 + 44 •4 - 20• 16/2 = 96 кН• м
x

27.

F
q
М
RА
В
А
2,2 м
44
+
36
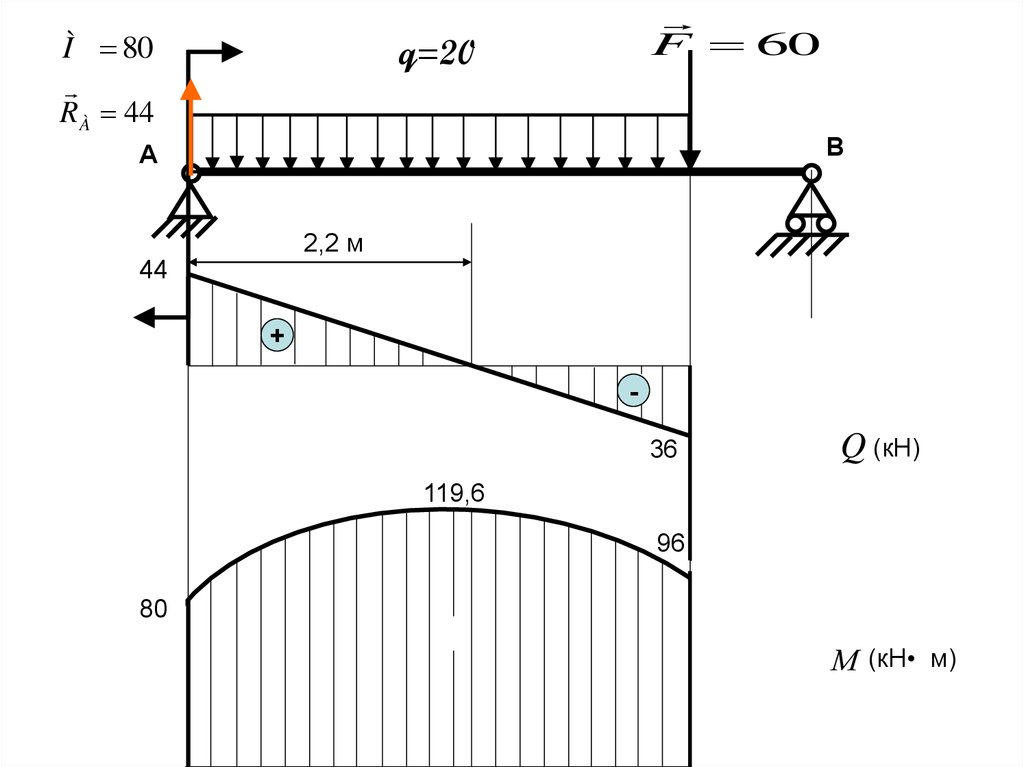
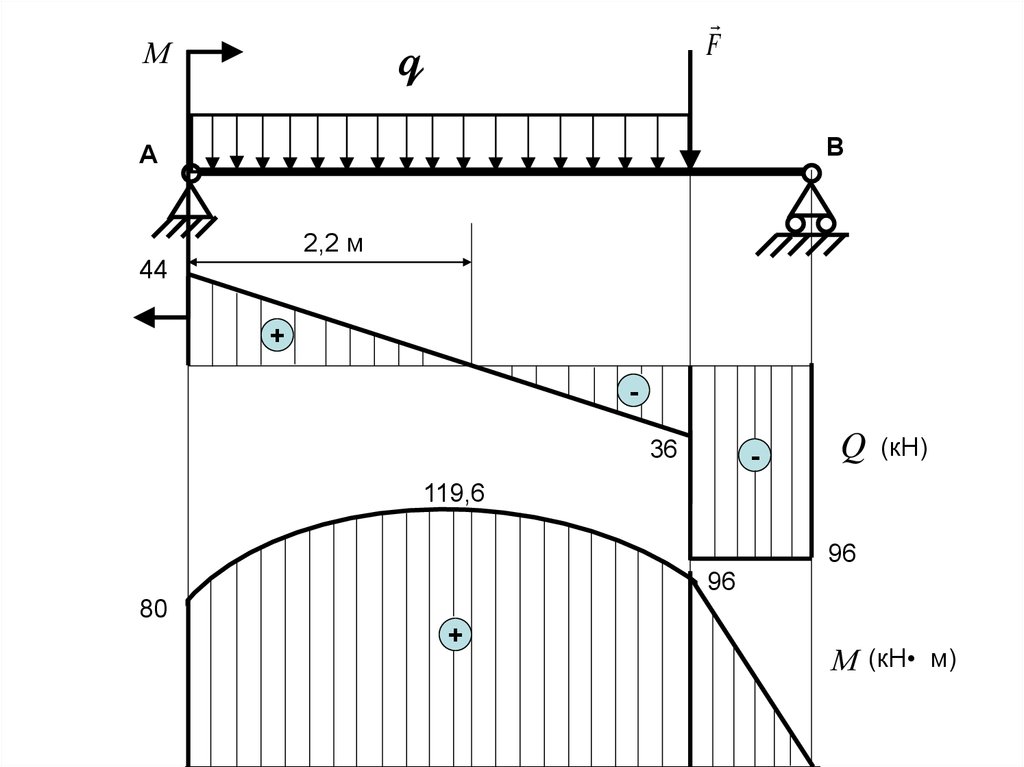
На эпюре
Q
- прямая,
Максимальным момент
80
-
Q
(кН)
128,4
М - парабола
М
будет в точке, когда96Q = 0 .
RА - q • x = 0, х = RА / q = 44/20
+ = 2,2 м.
М 1 (x=2,2) = 80 + 44• 2,2 -20• 2,2• 2,2/2 = 119,6 кН•м
М (кН• м)
(Так как q равно второй производной от М по х, а q отрицательно )

28.

Ì 80
R À 44
F 60
q=20
В
А
2,2 м
44
+
36
-
Q (кН)
119,6
96
96
96
80
М (кН• м)

29.

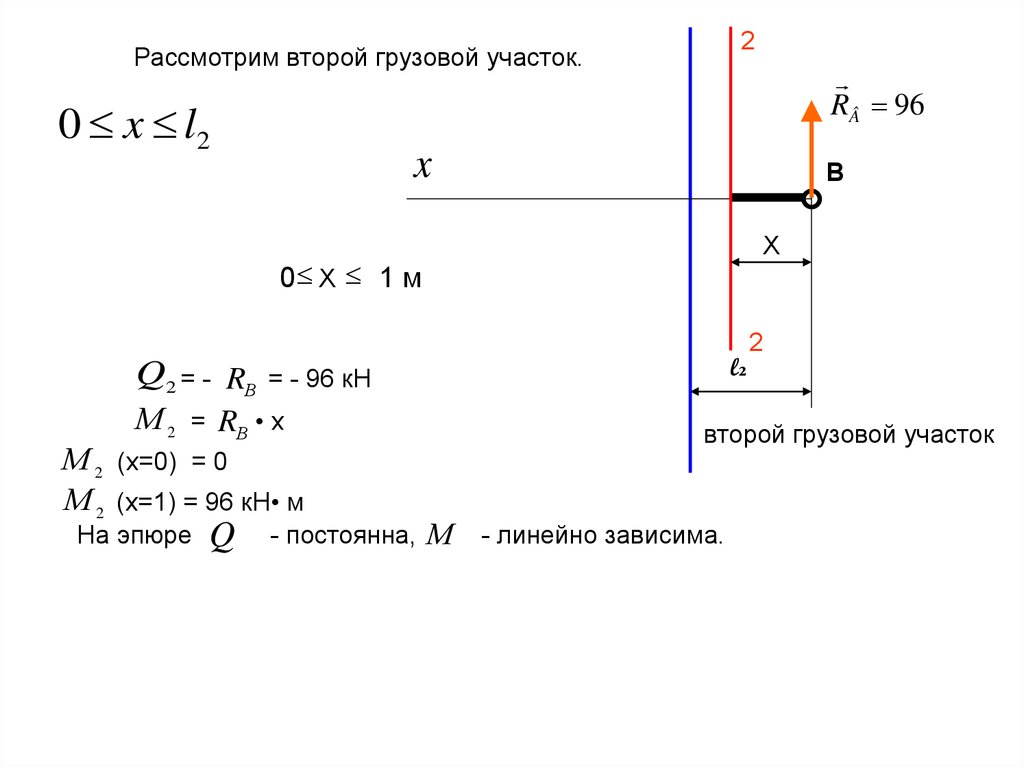
2
Рассмотрим второй грузовой участок.
0 x l2
RÂ 96
x
В
Х
0 Х 1 м
Q2 = - RВ
М 2 = RВ • х
М 2 (x=0) = 0
М 2 (x=1) = 96 кН• м
На эпюре
Q
l₂
= - 96 кН
- постоянна, М
2
второй грузовой участок
- линейно зависима.

30.

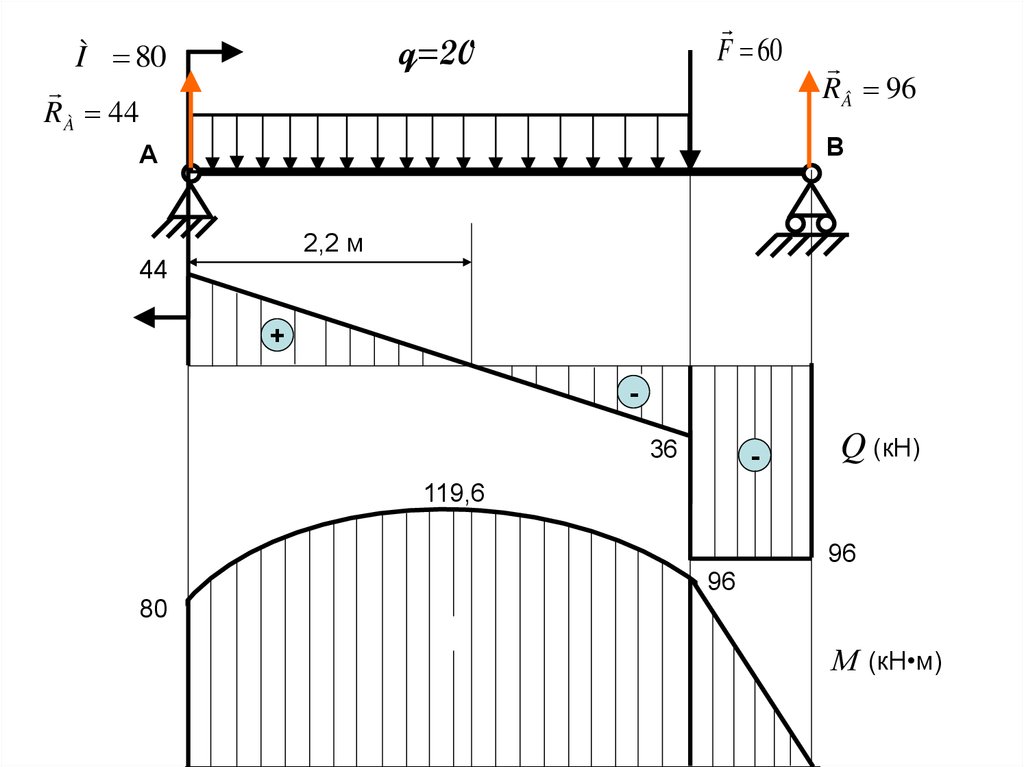
F 60
q=20
Ì 80
R À 44
RÂ 96
В
А
2,2 м
44
+
36
-
Q (кН)
119,6
96
96
80
М (кН•м)

31.

При проверке эпюр следует ось x мысленно всегда
направлять слева направо.
На участке, где нет распределенной нагрузки, эпюра моментов
представляет собой наклонную прямую, а эпюра
поперечных сил — прямую, параллельную оси.
На участке, где приложена равномерно распределенная
нагрузка, эпюра моментов представляет собой параболу, а
эпюра поперечных сип — наклонную прямую.
На конце балки изгибающий момент равен нулю, если там не
приложена пара сил.
При построении эпюры для консольных балок начало
координат удобно брать на конце консоли, что нередко дает
возможность обойтись без определения опорных реакций.
В сечении, соответствующем заделке, поперечная сила равна
реактивной силе, а изгибающий момент — реактивному
моменту.

32.

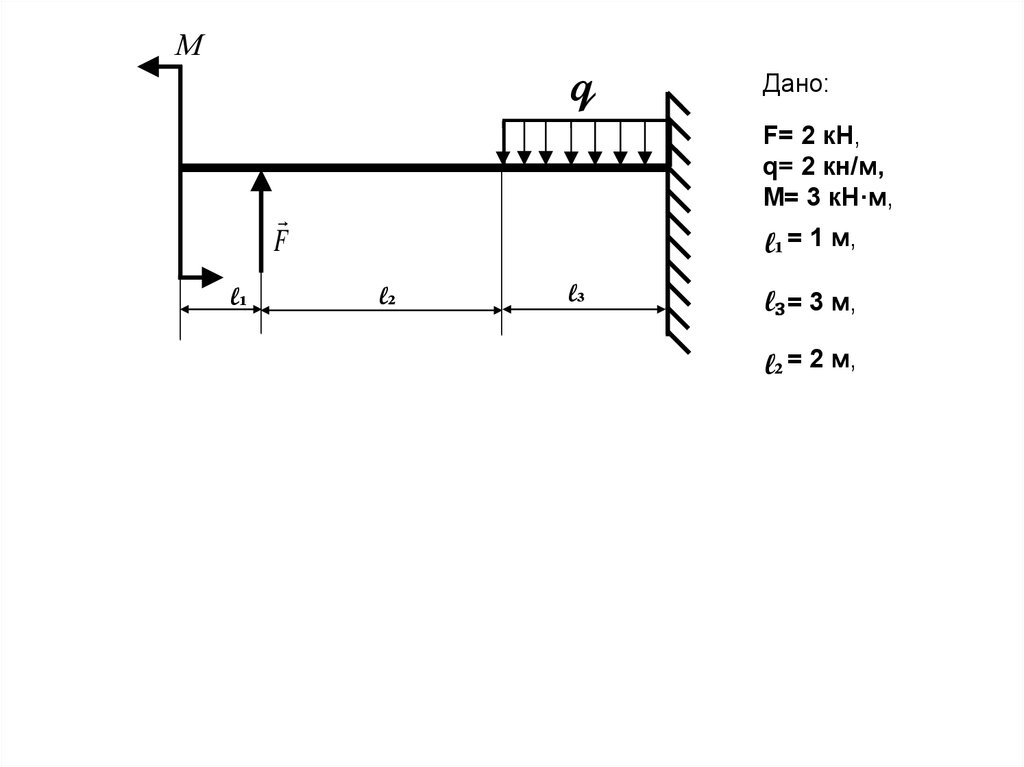
М
q
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
F
l₁
Дано:
l₁ = 1 м,
l₂
l₃
l₃ = 3 м,
l₂ = 2 м,

33.

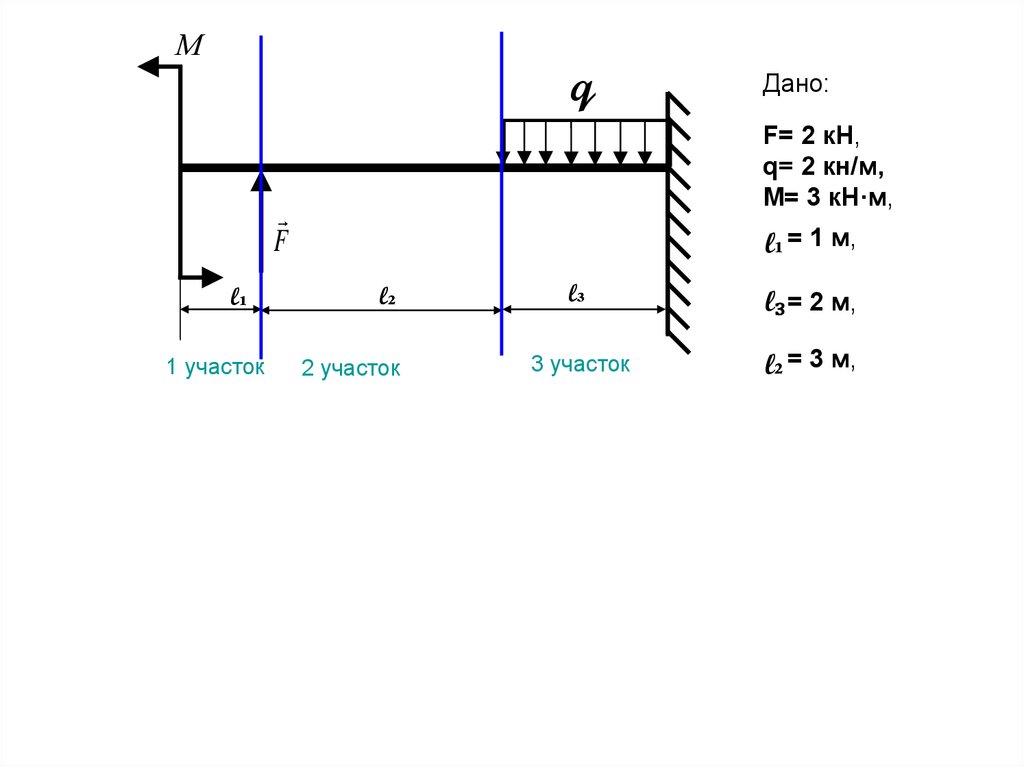
М
q
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
F
l₁
1 участок
Дано:
l₁ = 1 м,
l₂
2 участок
l₃
l₃ = 2 м,
3 участок
l₂ = 3 м,

34.

М
q
1
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
1 F
l₁
1 участок
Дано:
l₁ = 1 м,
l₂
2 участок
l₃
l₃ = 3 м,
3 участок
l₂ = 2 м,

35.

М
1
2
1 участок
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
1 F
l₁
q
l₁ = 1 м,
2
l₂
2 участок
l₃
l₃ = 3 м,
3 участок
l₂ = 2 м,

36.

М
3
1
2
1 участок
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
1 F
l₁
q
2
l₂
2 участок
3
l₃
3 участок
l₁ = 1 м,
l₃ = 3 м,
l₂ = 2 м,

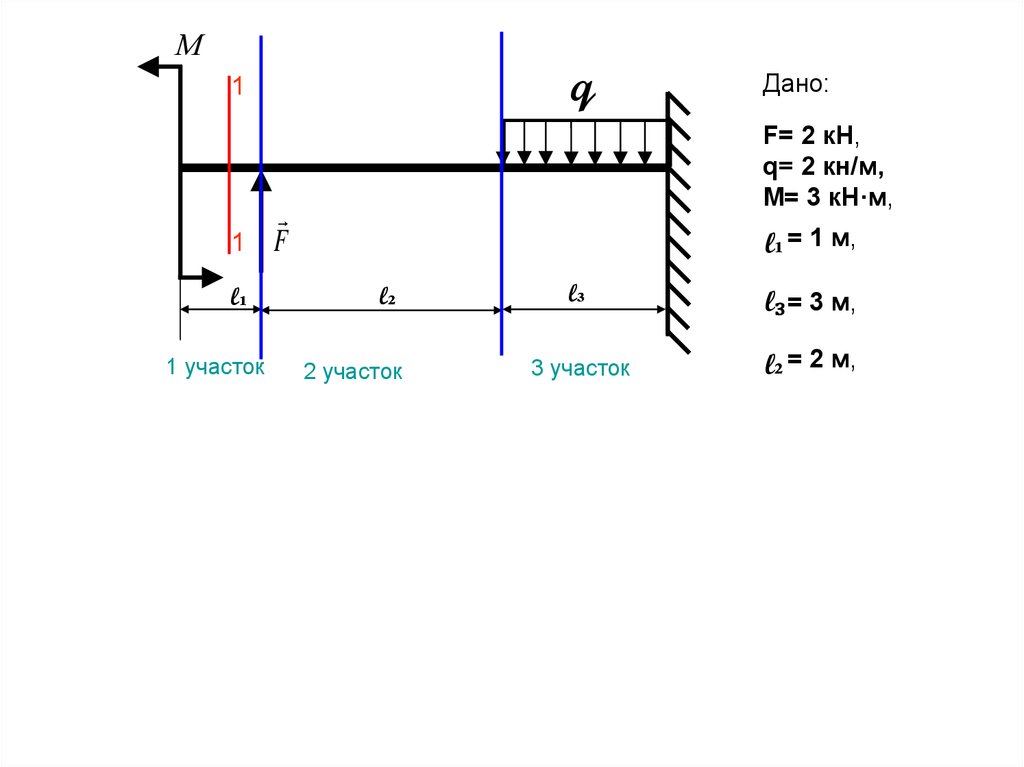
37.

М 3
3
q
2
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
x
F
х
l₁
1 участок
2
3
l₃
l₂
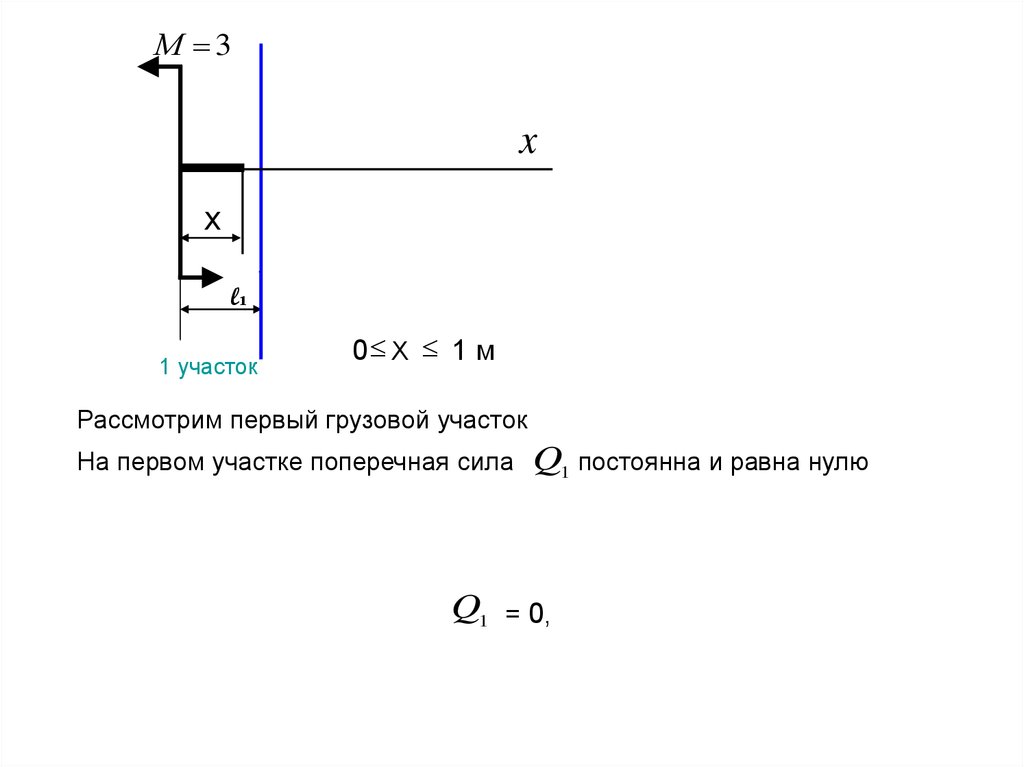
0 Х 1 м
1 участок
2 участок
Дано:
l₁ = 1 м,
l₃ = 3 м,
l₂ = 2 м,
Рассмотрим первый грузовой участок
На первом участке поперечная сила
Q1
Q1 постоянна и равна нулю
= 0,

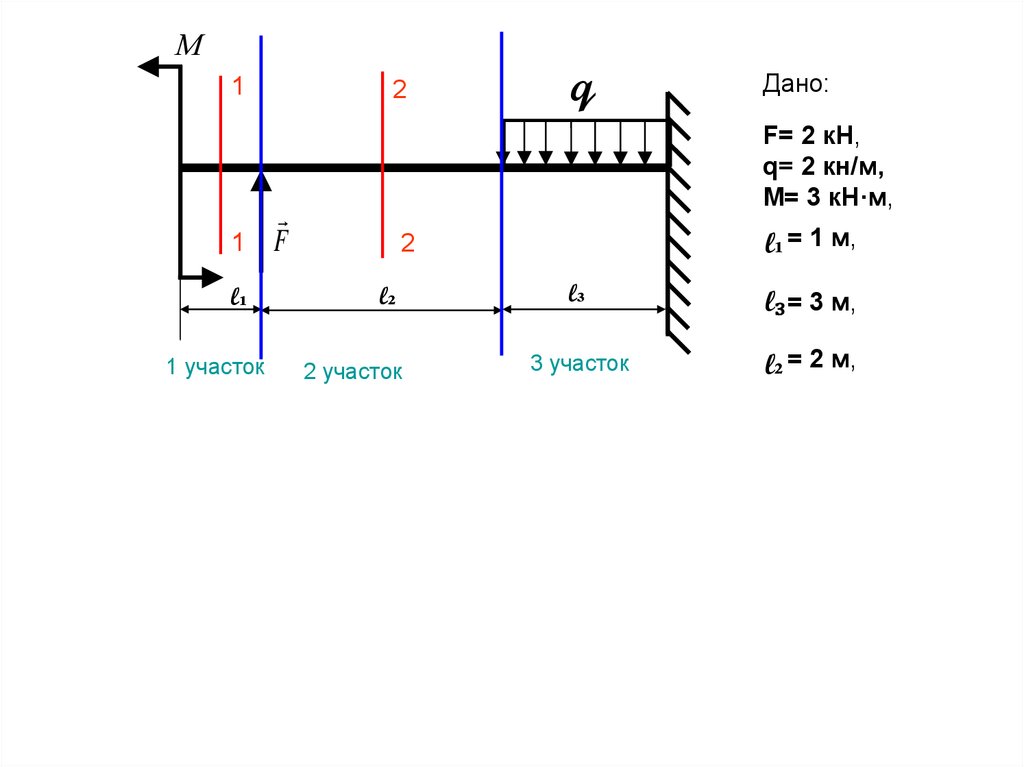
38.

М 3
3
q
2
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
x
F
х
2
3
l₃
l₂
l₁
1 участок
0 Х 1 м
2 участок
1 участок
В сечении на первом участке изгибающий момент
М1 = - М ,
М 1 = - 3 кН • м
Дано:
l₁ = 1 м,
l₃ = 3 м,
l₂ = 2 м,
М 1 равен

39.

М 3
Дано:
х
x
F 2
l₁ = 1 м,
l₂
l₁
1 участок
l₃ = 3 м,
l₂ = 2 м,
2 участок
1 Х 4м
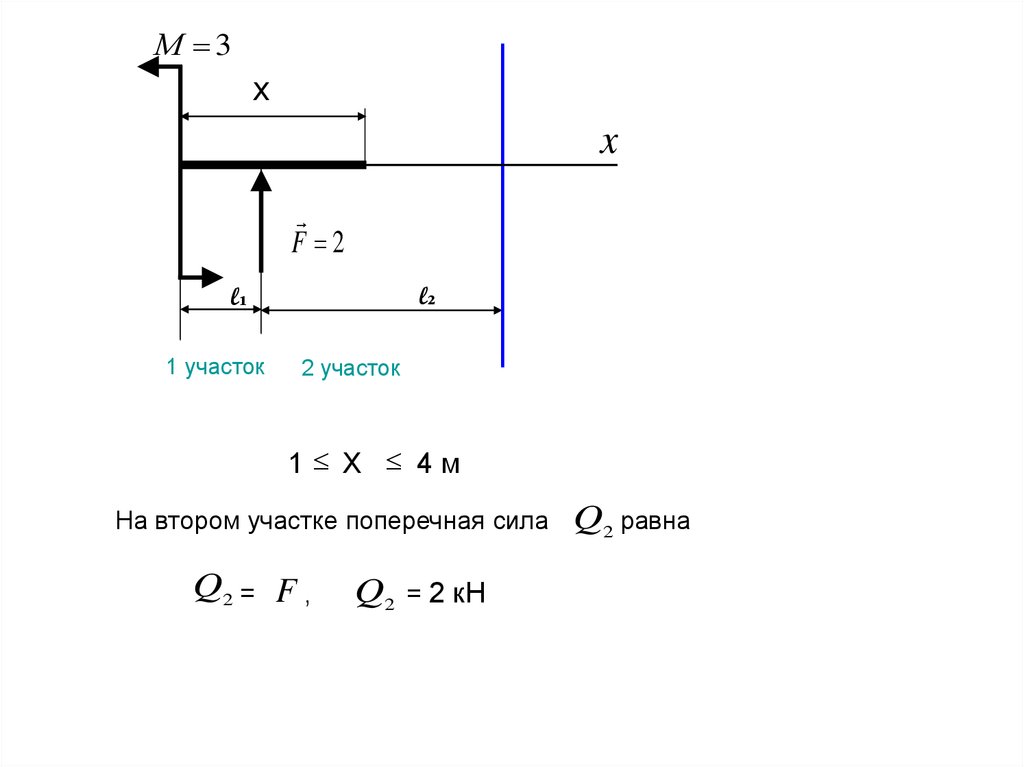
На втором участке поперечная сила
Q2 = F ,
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
Q2 = 2 кН
Q2 равна

40.

М 3
Дано:
х
x
F 2
l₁ = 1 м,
l₂
l₁
1 участок
l₃ = 3 м,
l₂ = 2 м,
2 участок
1 Х 4м
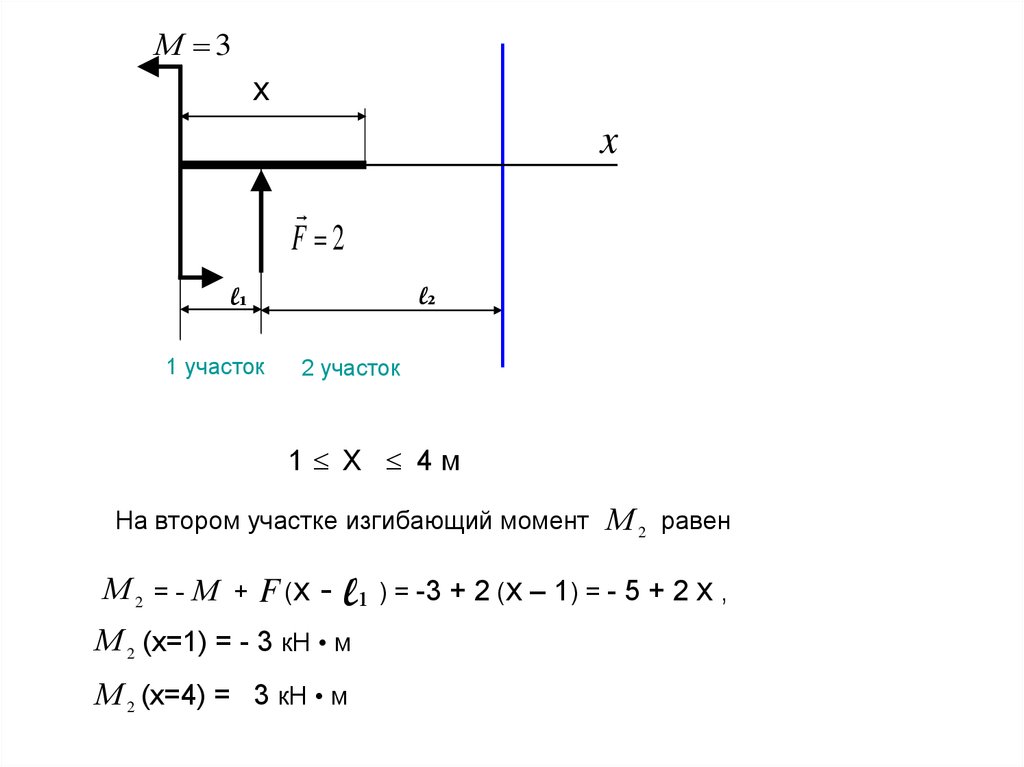
На втором участке изгибающий момент
М 2 = - М + F (х -
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
М 2 равен
l₁ ) = -3 + 2 (х – 1) = - 5 + 2 х ,
М 2 (x=1) = - 3 кН • м
М 2 (x=4) = 3 кН • м

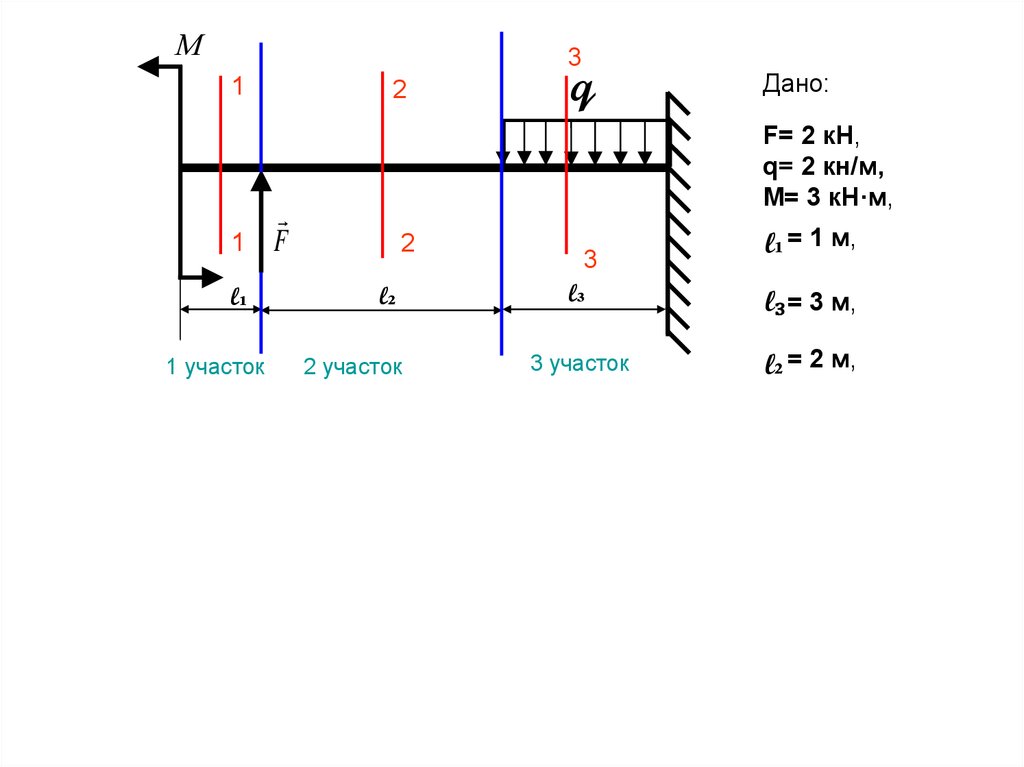
41.

М 3
q=2
х
x
F 2
l₃
l₂
l₁
1 участок
2 участок
3 участок
4 Х 6м
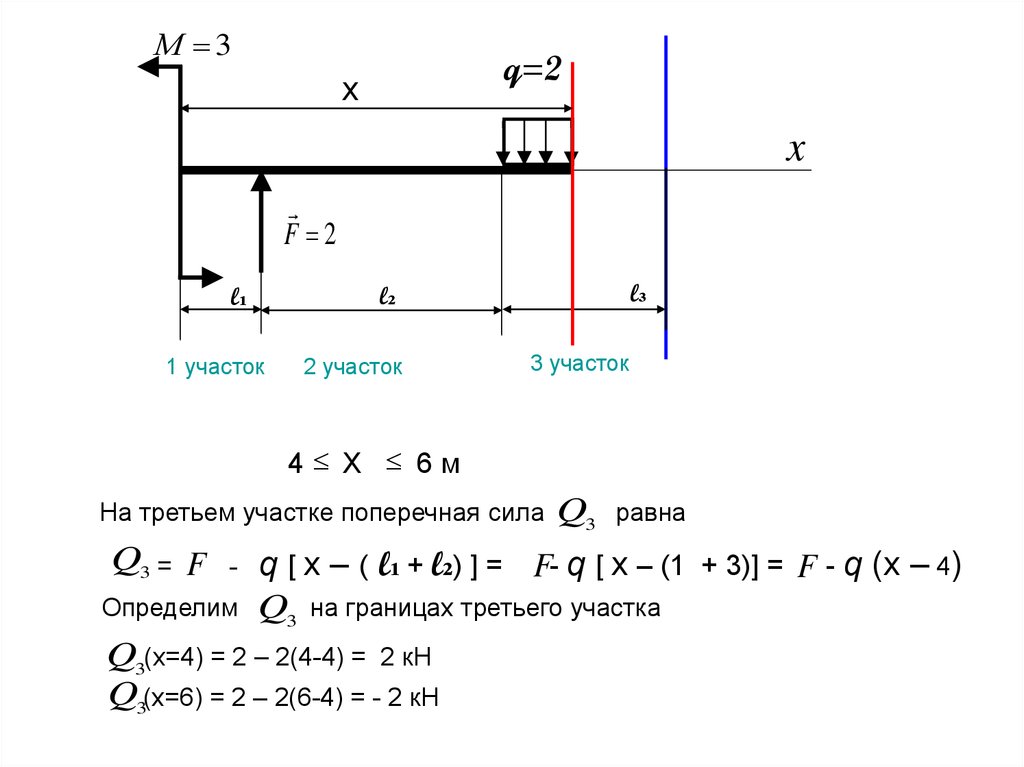
На третьем участке поперечная сила
Q3 = F
-
Определим
Q3
равна
q [ х – ( l₁ + l₂) ] = F- q [ х – (1 + 3)] = F - q (х – 4)
Q3 на границах третьего участка
Q3(x=4) = 2 – 2(4-4) = 2 кН
Q3(x=6) = 2 – 2(6-4) = - 2 кН

42.

М 3
q=2
х
x
F 2
l₁
1 участок
l₃
l₂
2 участок
3 участок
4 Х 6м
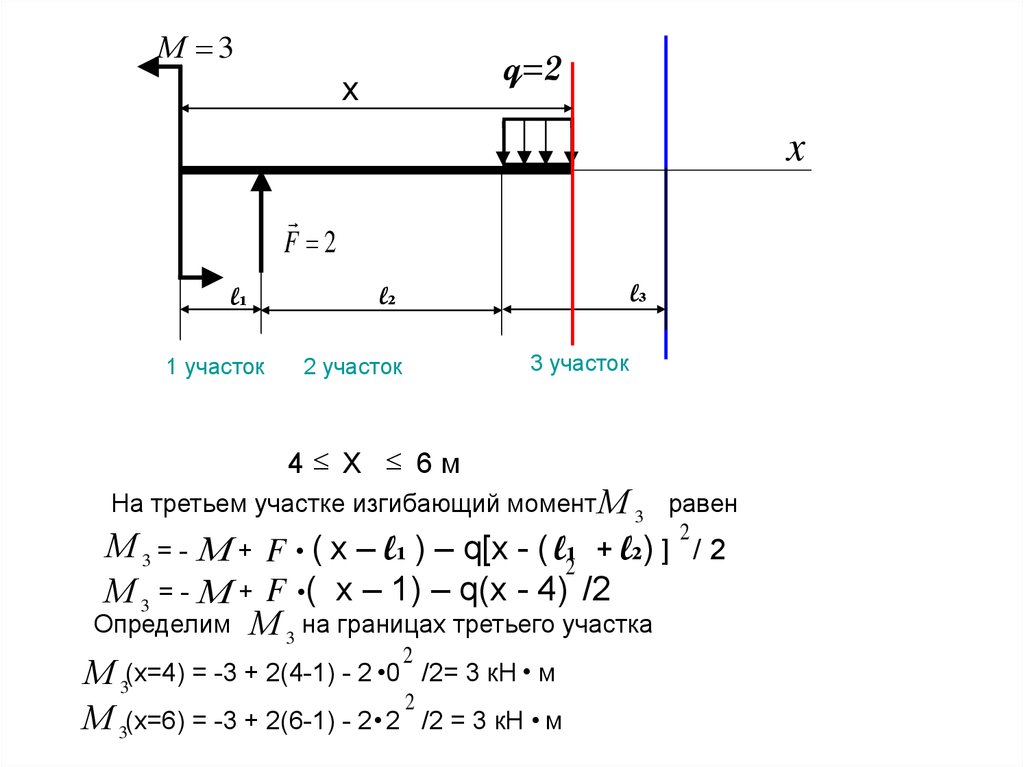
На третьем участке изгибающий момент М 3 равен
2
М 3 = - М + F • ( х – l₁ ) – q[х - ( l₁2 + l₂) ] / 2
М 3 = - М + F •( х – 1) – q(х - 4) /2
Определим М 3 на границах третьего участка
2
(x=4)
=
-3
+
2(4-1)
2
0
/2= 3 кН • м
М3
2
М 3(x=6) = -3 + 2(6-1) - 2 • 2 /2 = 3 кН • м

43.

dM
Если Q =
= 0, то изгибающий момент имеет максимум.
dx
Q3 = F - q (х – 4) = 0
2-2 (х – 4)=0 , х = 5 м
Максимум момента равен 4 кН• м

44.

М 3
q=2
F 2
l₁ =1
Q1 = 0 кН
Q2 = 2 кН
Q3 (x=4) = 2 кН
Q3(x=6) = - 2 кН
l₃=2
l₂ =3
2
2
+
Q (кН)
4
3
-
2
3
М 1 = - 3 кН • м
М 2 (x=1) = - 3 кН • м
М 2 (x=4) = 3 кН • м
М (кН• м)
3
М 3(x=4) = 3 кН • м
М 3(x=6) = 3 кН • м

45.

При построении эпюр следует руководствоваться
приведенными правилами:
Эпюру моментов строят на сжатом волокне, т. е. положительные
моменты (и положительные поперечные силы) откладывают вверх
от оси, а отрицательные — вниз.
Пользуясь принципом смягченных граничных условий, будем
полагать, что в сечении, где приложена сосредоточенная сила,
значение поперечной силы меняется скачкообразно, причем скачок
равен модулю этой силы.
На том же основании будем полагать, что в сечении, где
приложена пара сил (момент), значение изгибающего момента
меняется скачкообразно, причем скачок равен моменту пары.
Если в каком-либо сечении балки приложена сосредоточенная
сила, то на эпюре поперечных сил в этом сечении будет скачок на
величину силы, а на эпюре изгибающих моментов произойдет
излом эпюры.
Если участок балки загружен равномерно распределенной нагрузкой q, то на эпюра поперечных сил на этом участке ограничена
наклонной прямой, а эпюра моментов – кривой второго порядка.

46.

Правильность построения эпюр Q и М следует проверять с
помощью теоремы Журавского:
Между изгибающим моментом, поперечной силой и интенсивностью
распределенной нагрузки существуют дифференциальные
зависимости, основанные на теореме Журавского.
Эта теорема формулируется так: поперечная сила равна
первой производной от изгибающего момента по
абсциссе сечения балки.
dM
d 2M
dQ
q= dx = dx2
Q = dx = tg ,
где — угол, который составляет касательная к эпюре моментов с
положительным направлением оси x.

47.

Расчет балки на прочность и жесткость при изгибе.
Дано:
1.Расчетная схема балки.
2.Эпюры поперечных сил и изгибающих моментов, построенные для
заданной расчетной схемы.
3.Допускаемые нормальные [ ] и касательные напряжения
материала балки: [ ] =160 МПа,
[ ] =100 МПа.
4.Модуль упругости материала балки
5.Допускаемый прогиб балки
балки длиной
lп
и
[ ]
Е 2 105 МПа .
lп
- для однопролетной
y
300
lк
y
200
- консольной балки длиной
lк
.

48.

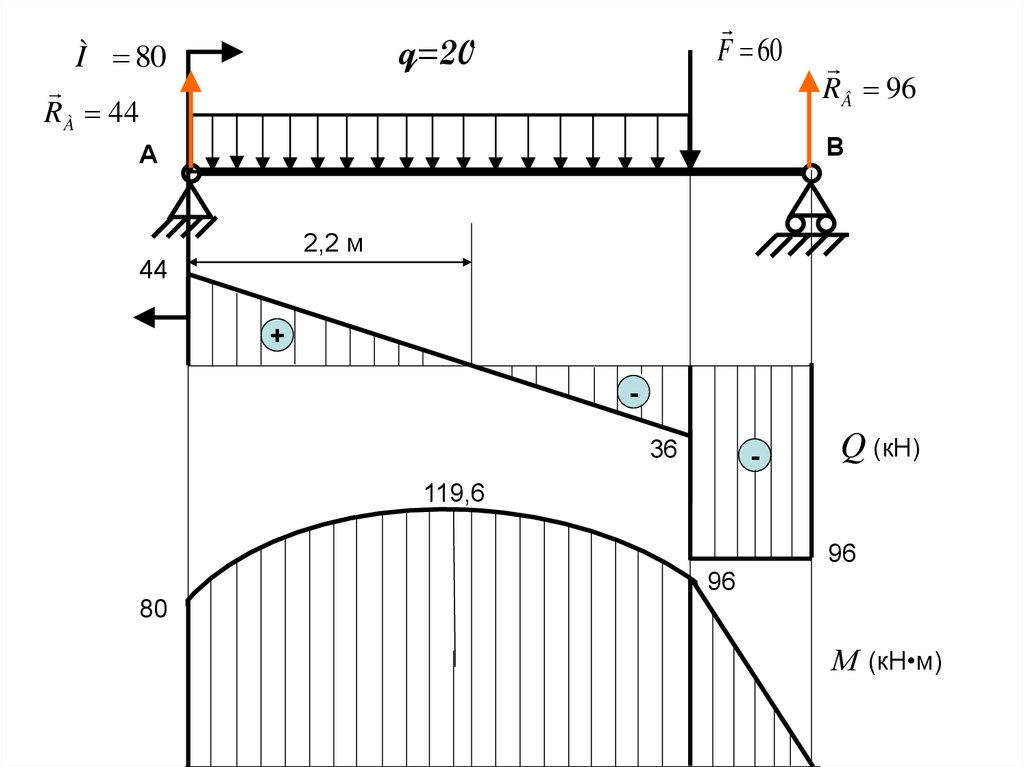
F 60
q=20
Ì 80
R À 44
RÂ 96
В
А
2,2 м
44
+
36
-
Q (кН)
119,6
96
96
80
М (кН•м)

49.

Требуется
1. Из условия прочности определить размеры прямоугольного сечения
балки при
h
2
b
(
h
и
b– соответственно высота и ширина сечения ).
2. Подобрать по сортаменту прокатной стали номер двутавра, удовлетворяющий
условию прочности.
3. Сравнить по весу балки прямоугольного и двутаврового поперечного сечений
и определить экономию материала при изготовлении двутавровой балки.
4. Для каждой из двух балок построить эпюры распределения нормальных
напряжений
по высоте опасного сечения, где
М x | M x max |.
5. Для каждого из двух сечений балок построить эпюры распределения касательных
напряжений
по высоте опасного сечения, в котором
Qx | Qx max |
6. Проверить прочность балок по касательным напряжениям.

50.

7. Построить эпюры углов поворота
и прогибов
y
для двутавровой балки.
8. Проверить двутавровую балку на жесткость.
9. Если условие жесткости не выполняется, определить новый номер двутавра,
для которого условие будет выполнено.

51.

Решение.
1. Определение размеров прямоугольного поперечного сечения балки.
Из эпюры
М x определяется максимальное значение изгибающего момента M x max
М x 119,6кН м
М max
[ ] определяем размеры
Из условия прочности
Wн .о
h .
прямоугольника поперечного сечения балки при
2
b
max-максимальное по абсолютной величине расчетное нормальное напряжение
в опасном сечении.
М max - максимальный изгибающий момент по абсолютной величине из эпюры.
Wн .о -момент сопротивления поперечного сечения балки относительно
нейтральной оси.
[ ] - допускаемое нормальное напряжение материала балки.

52.

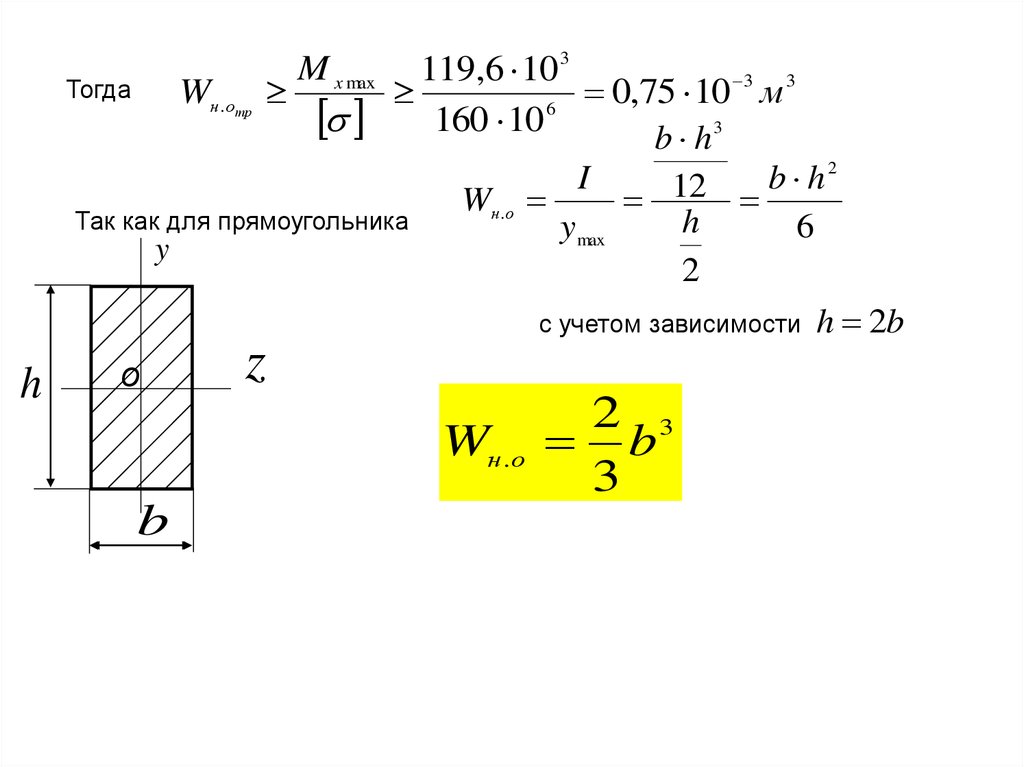
Wн.о
Тогда
тр
M x max
119,6 10 3
3
3
0
,
75
10
м
160 10 6
b h3
Так как для прямоугольника
Wн.о
y
h
o
z
Wн .о
b
2
b
h
12
h
y max
6
2
с учетом зависимости h 2b
I
2 3
b
3

53.

bтр 3
Значение
значения
3Wн.о
тр
2
bтр
3
3 0,75 10 3
1,04 10 1 м 104 мм
2
обычно округляют в большую сторону до стандартного
b bтр.
b 104 мм 11см
h 22см
По данным значениям определяется уточненное значение
Wн .о
Wн .о
.
b h2
110 484 10 2
887 10 3 мм 3 0,887 10 3 м 3
6
6
Wн.о 0,75 10 3 м3
условие выполняется.

54.

2. Выбор номера двутавра.
По сортаменту прокатной стали и найденному значению
Wн .о
тр
определяется
номер двутавра, удовлетворяющий условию прочности
Wн.о 0,75 10 3 м3 750см 3
тр
Выбираем двутавр с ближайшим большим значением
Wн.о
ст
(по сортаменту)
Wz
по сравнению с требуемым значением
Wн.о 947см 3
ст
Wн .о
тр
.

55.

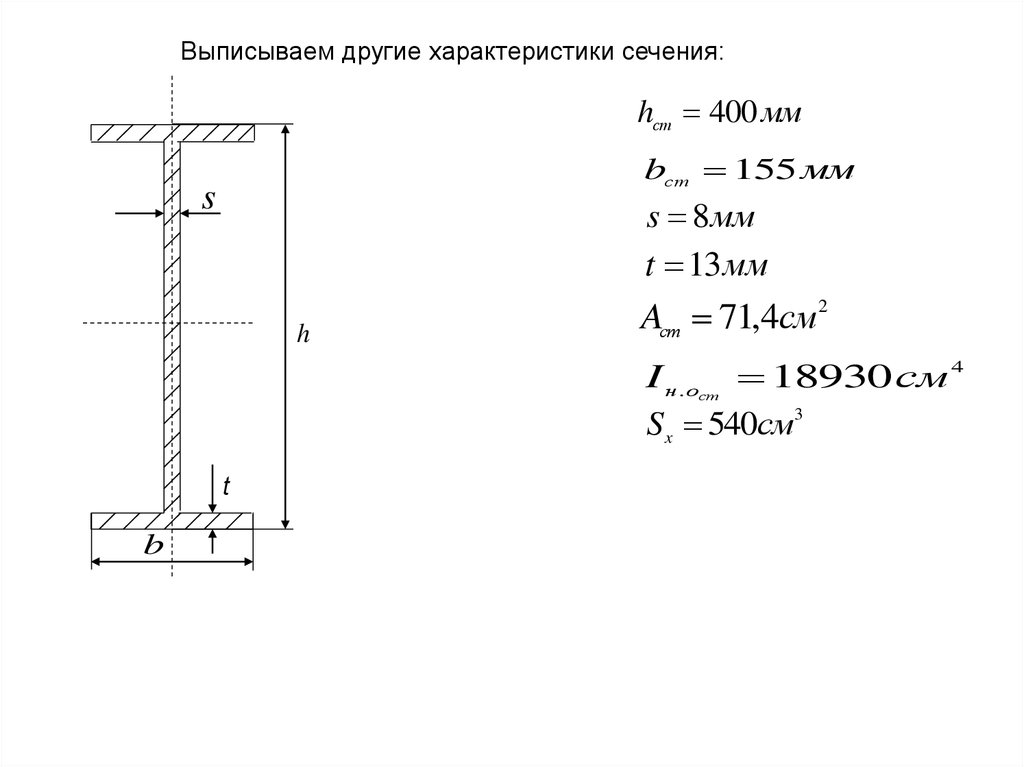
Выписываем другие характеристики сечения:
hст 400 мм
bст 155 мм
s
s 8 мм
t 13 мм
h
Aст 71,4см2
I н .о 18930см 4
Sx 540см3
ст
t
b

56.

3.Сравнение по весу балок прямоугольного сечения и двутаврового
поперечных сечений через коэффициент экономичности Э.
Gдв Аст Аст
Э
Gпр Апр b h
G дв , Gпр
- соответственно вес балок двутаврового и прямоугольного
cечений;
Аст и Апр b h
соответственно площади двутаврового и
прямоугольного поперечных сечений балок.
71,4
Э
0,295
242
По численному значению коэффициента Э делается вывод о достоинствах
двутавровой балки.

57.

4.Строим эпюры распределения нормальных напряжений по высоте
опасного сечения.
max
Распределение напряжений
подчиняется закону
y
М max
Wн.о
в опасном сечении при изгибе
| M max | y
I н .о
.
- расстояние от рассматриваемой точки до нейтральной оси сечения;
относительно нейтральной оси
I н .о- момент инерции поперечного сечения балки
3
Для прямоугольного сечения
Так как напряжения
I н .о
b h
12
пропорциональны расстоянию
y
от нейтральной
оси сечения до рассматриваемой точки, эпюру строим по двум точкам.

58.

При
При
Из
Wн.о
max
y 0
y y max
имеем
h
2
I н .о b h 2
ymax
6
M x max
Wн.о
0
получаем
| M max | y
I н .о
max
, полученного ранее для прямоугольного сечения
для максимальных напряжений в балках прямоугольного
и двутаврового сечений.
Напряжения
имеют знак «+» с той стороны нейтральной оси сечения,
где волокна балки растянуты, и знак «-», где волокна сжаты.

59.

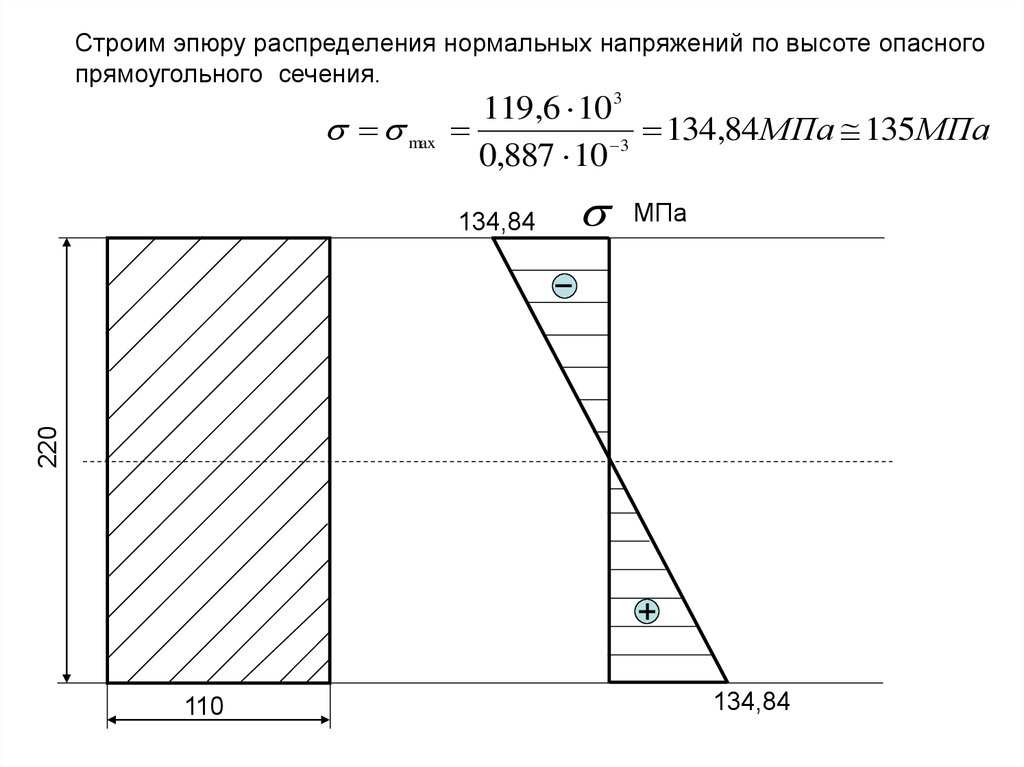
Строим эпюру распределения нормальных напряжений по высоте опасного
прямоугольного сечения.
max
119,6 10 3
134,84 МПа 135 МПа
3
0,887 10
МПа
220
134,84
110
134,84

60.

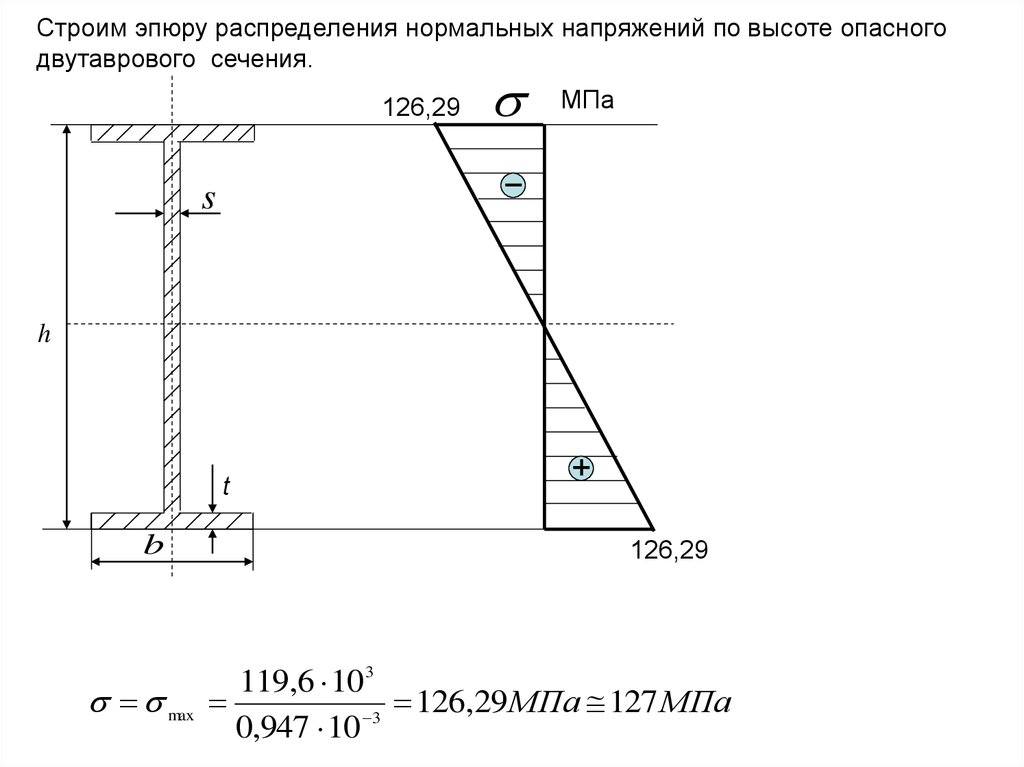
Строим эпюру распределения нормальных напряжений по высоте опасного
двутаврового сечения.
126,29
МПа
s
h
t
b
max
126,29
119,6 10 3
126,29 МПа 127 МПа
3
0,947 10

61.

5. Определение касательных напряжений и построение эпюр распределения
касательных напряжений
по высоте полного и двутаврового опасного
сечений.
Из эпюры поперечных сил
величине значение
Qx
определяется максимальное по абсолютной
| Qx max | 96кН
.
В произвольной точке прямоугольного сечения балки касательное напряжение
y
определяют по формуле Журавского:
b
Q S н*.о
I н .о b
h
y
I н .о -момент инерции всего сечения
yС
н.о
z
относительно нейтральной оси
S н*.о - статический момент относительно нейтральной оси z части
площади сечения, лежащей по одну сторону от уровня y , на котором
определяется напряжение;
b - ширина сечения на уровне данной точки

62.

Формула Журавского читается так:
Касательные напряжения в поперечном сечении балки равны произведению
поперечной силы
Q
на статический момент
S н*.о
относительно нейтральной
оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному
на момент инерции
ширину
S
*
н .о
I н .о
всего сечения относительно нейтральной оси и на
b рассматриваемого слоя волокон.
h
y
2
h
b h
2
2
yc A b ( y ) (
y) ( y )
2
2
2 4

63.

Зависимость
момент
S z*
от
y
в сечении определяется через статический
.При подходе к верхней кромке сечения площадь его
заштрихованной части уменьшается до нуля. Здесь, следовательно
Для стержня прямоугольного сечения со сторонами
b h2
Sz ( y2 )
2 4
распределение напряжений
, следовательно
в прямоугольном сечении подчиняется закону
Q | Qx max | 96кН
6Qmax h 2
2
(
y
)
3
b h 4
max
При
3Q
2b h
.
bи h
b h2
Q ( y2 )
*
Q S н .о
6 Q h2
2
2
4
(
y
)
3
3
b h
I н .о b
bh
4
b
12
Итак, для расчетов
S z* 0
h
y
2
y 0
0 , а при
max

64.

max
3 96 10
5,95 10 6 Па 5,95МПа
2 0,11 0,22
max
3
при
h
y
4
будет равно
3Q
2b h
6Qmax h 2
2
(
y
)
3
b h 4
6 Q h2 h2
6 Q 3h 2 18Q
9Q
9Q
3 ( ) 3
2
bh
4 16
bh 16 16bh 8 2 b 16b 2
h
4
9 96 103
h
4,46 106 Па 4,46МПа
16 0,0121
4
Таким образом, в верхнем и нижнем слоях волокон касательные напряжения
равны нулю, а в волокнах нейтрального слоя они достигают максимального
начения.

65.

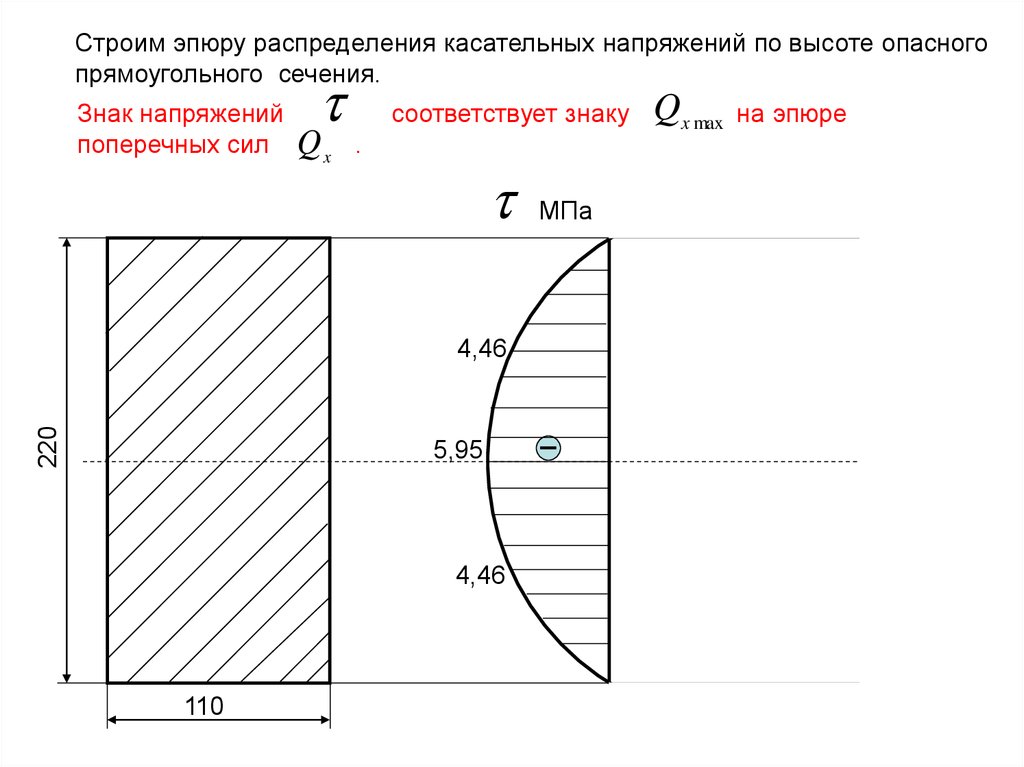
Строим эпюру распределения касательных напряжений по высоте опасного
прямоугольного сечения.
Знак напряжений
поперечных сил
Qx
соответствует знаку
.
220
4,46
5,95
4,46
110
МПа
Qx max
на эпюре

66.

Для двутавровой балки напряжение
сечения по формуле Журавского
определяется в отдельных слоях
Qmax S
i
bi I н.ост
*
i
Si*
-статический момент относительно нейтральной оси части сечения,
расположенный по одну сторону от рассматриваемого слоя i
- ширина рассматриваемого слоя
bi
I н.о ( I z ) -момент инерции поперечного сечения балки относительно
ст
нейтральной оси
b1 b2 b6 b7 bст
b3 b4 b5 S

67.

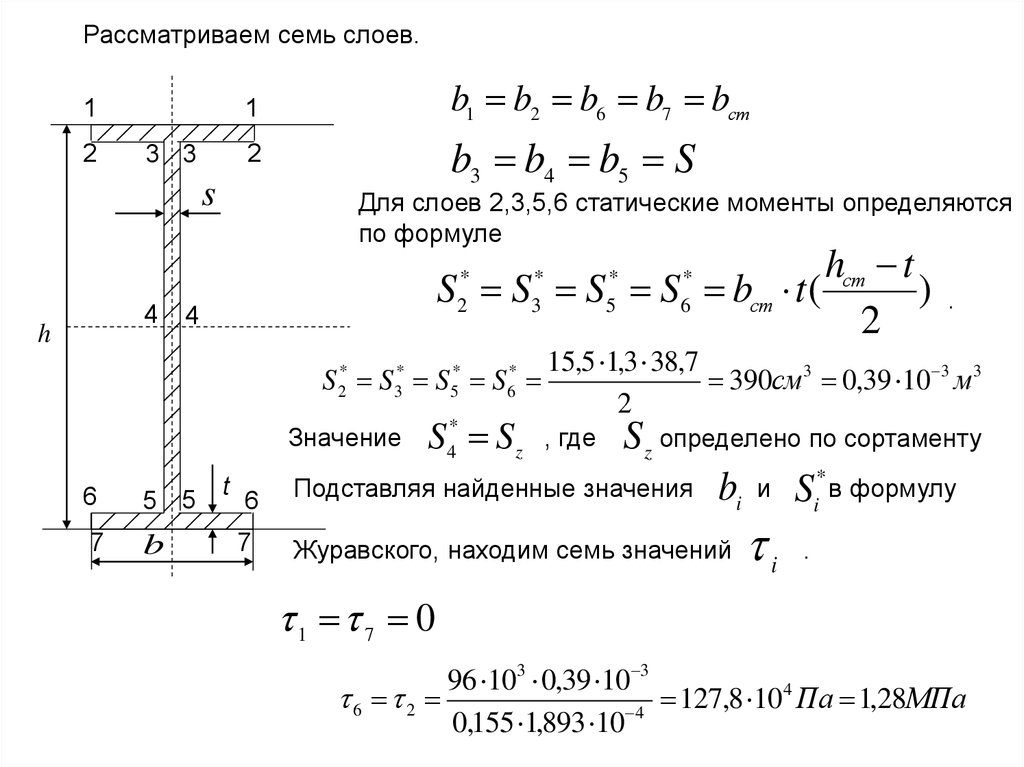
Рассматриваем семь слоев.
1
2
3 3
1
b1 b2 b6 b7 bст
2
b3 b4 b5 S
s
4
h
Для слоев 2,3,5,6 статические моменты определяются
по формуле
hст t
S S S S bст t (
)
2
*
2
4
*
3
S 2* S3* S5* S 6*
5 5
7
b
t
*
6
.
15,5 1,3 38,7
390см 3 0,39 10 3 м 3
2
6
S z определено по сортаменту
*
Подставляя найденные значения bi и S в формулу
i
7
Журавского, находим семь значений
Значение
6
S4* S z
*
5
, где
i
.
1 7 0
96 103 0,39 10 3
4
6 2
127
,
8
10
Па 1,28МПа
4
0,155 1,893 10

68.

96 10 3 0,39 10 3
7
3 5
2
,
48
10
Па 24,8МПа
3
4
8 10 1,893 10
96 10 3 0,54 10 3
7
4
3
,
42
10
Па 34,2МПа
3
4
8 10 1,893 10
Строим эпюру напряжений
с указанием знака напряжений.

69.

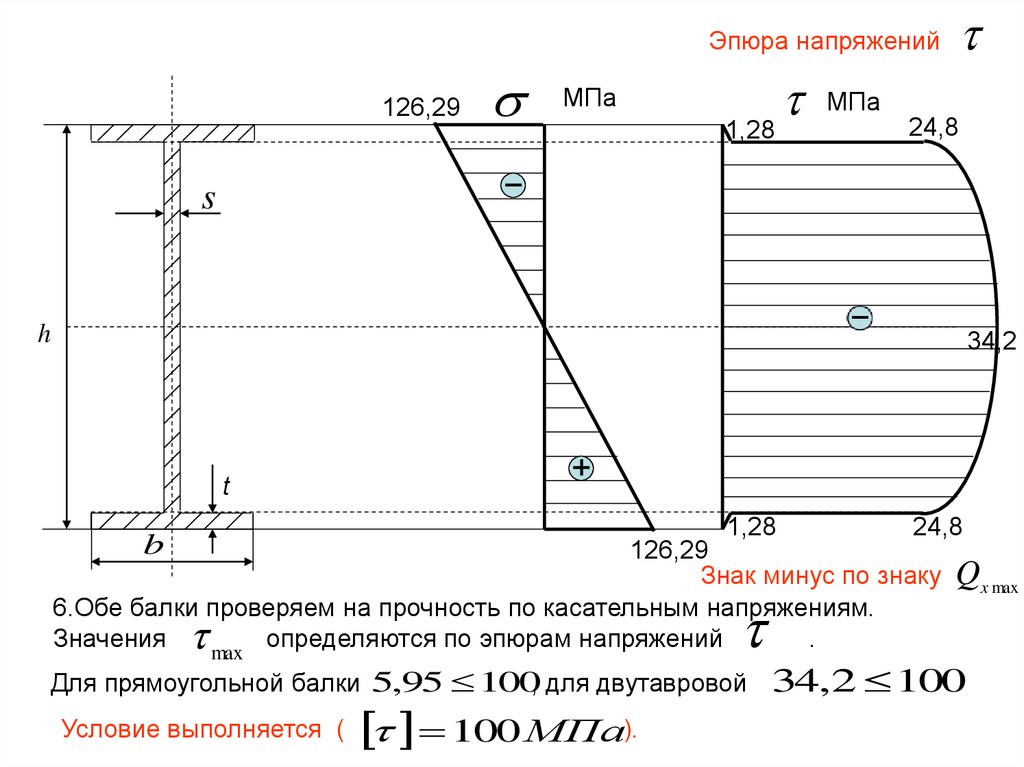
Эпюра напряжений
126,29
МПа
1,28
МПа
24,8
s
h
34,2
t
1,28
b
24,8
126,29
Знак минус по знаку
6.Обе балки проверяем на прочность по касательным напряжениям.
Значения
определяются по эпюрам напряжений
.
max
Для прямоугольной балки 5,95 100, для двутавровой
Условие выполняется (
100 МПа).
Qx max
34,2 100

70.

Определение деформации и проверка жесткости балки при изгибе..
Перемещения сечений балки характеризуется:
1) Прогибами y - линейными перемещениями центров тяжести
поперечных сечений в направлении, перпендикулярном к геометрической
оси балки x ;
2) углами поворота сечений
- угловыми перемещениями поперечных
сечений относительно нейтральной оси z.
Рассмотрим метод начальных параметров.
Универсальные уравнения для определения углов поворота сечений
и прогибов балок имеют вид:
1
1
1
EJ EJ 0 M i ( x ai ) Fj ( x b j ) 2 qk ( x сk )3
1!
2!
3!
1
1
1
2
3
EJy EJ y0 EI x M i ( x ai ) Fj ( x b j ) qk ( x сk ) 4
2!
3!
4!

71.

где
y0 , 0
ai , b j , ck
- соответственно прогиб и угол поворота в начале координат;
- расстояния от точек приложения M, F и начала распределенной
нагрузки до начала координат соответственно.
При определении прогибов и углов поворота этим методом необходимо:
1) все сечения отсчитывать от начала координат, расположенном в левом
конце стержня;
2) распределенную нагрузку продолжать в положительном направлении
оси
до конца балки и для ее уравновешивания прикладывать
нагрузку такой же интенсивности, но другого знака;
3) знаки сумм ( ) распространять на все нагрузки, расположенные
слева от того сечения балки, для которого определяется прогиб и
угол поворота сечения.
4) знаки слагаемых в обобщенных уравнениях устанавливают по правилу
знаков для изгибающих моментов.
x

72.

Начальные параметры y 0 и 0 , входящие в уравнение оси изогнутой балки,
определяются из условий закрепления балки.
Для балки на двух опорах известно, что прогибы на опорах равны нулю
y A yB 0
Для балки, левый конец которой лежит на опоре
0
0 0
и
y0 0
.
определяется из уравнения прогибов на второй опоре т.е.
yB 0
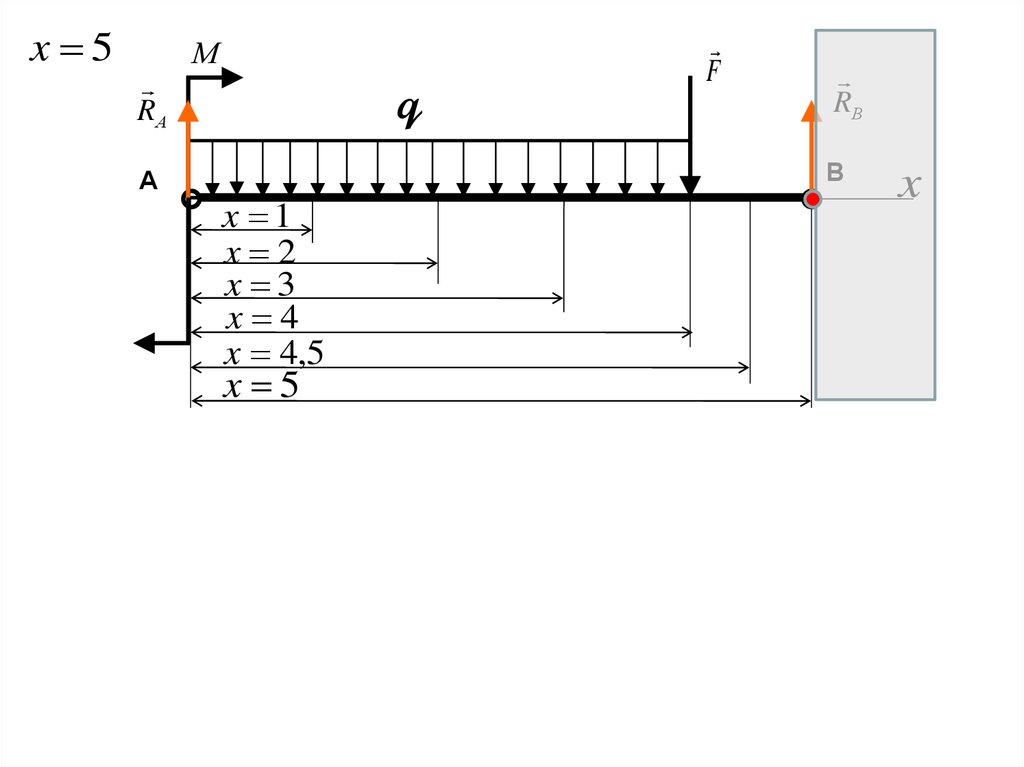
при
x 5
M 52 RA 53 F (5 4)3 q 54 q(5 4) 4
EIyb EIy0 EI 0 5
2
6
6
24
24
80 25 44 125 60 1 20 625 20 1
EIyb EI 0 EI 0 5 (
) 103
2
6
6
24
24
EI 0 5 (1000 916,6 10 520,8 0,83) 103 EI 0 5 1386,6 103 0
3
1386,6 103
EI 0
277,3 10
5
3
277,3 10
4
0
7
,
3
10
0,007 рад
11
4
2 10 1,89 10

73.

RА
А
М
F
q
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x 5
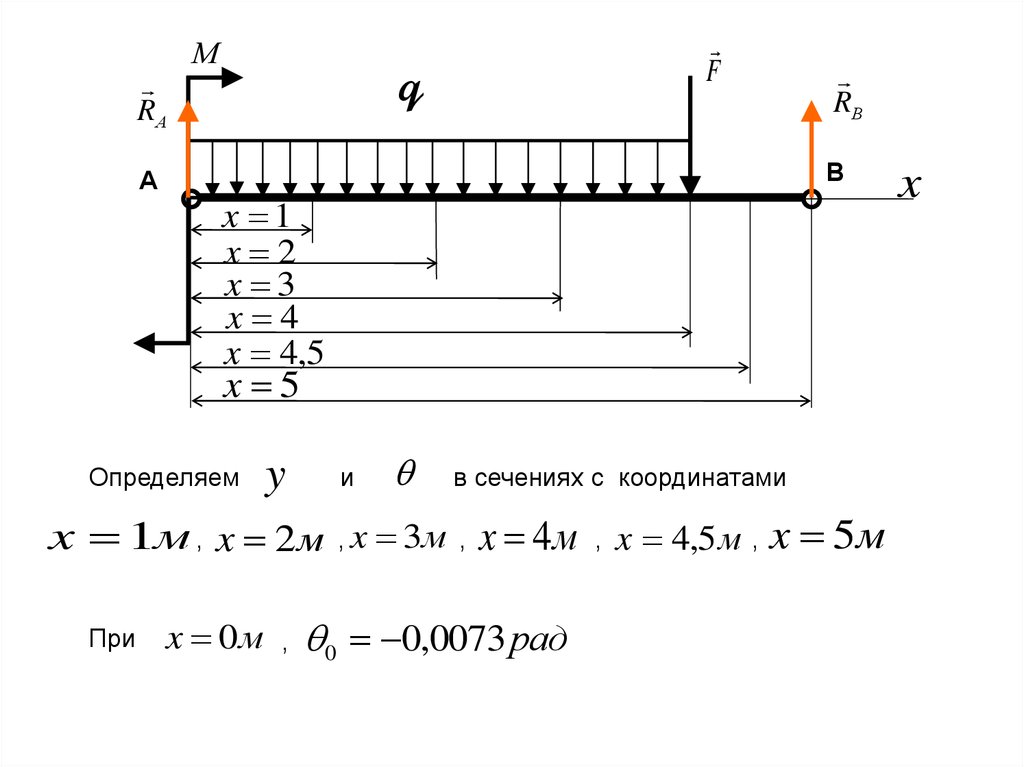
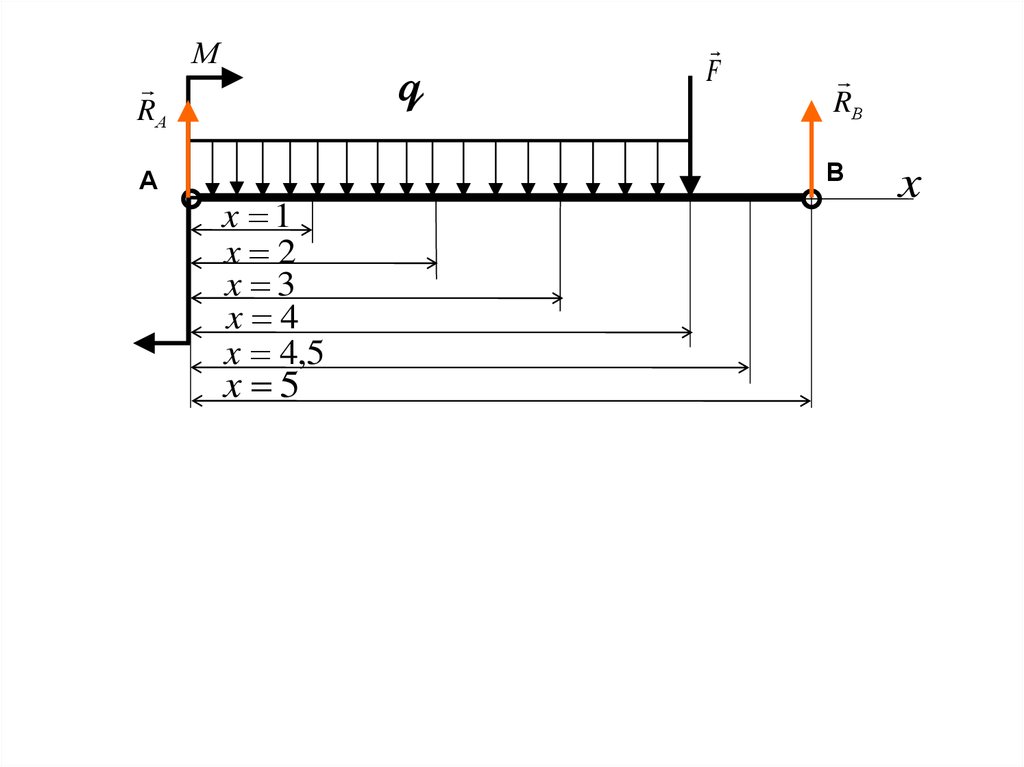
Определяем
y
и
в сечениях с координатами
x 1м , x 2 м , x 3м , x 4м , x 4,5 м , x 5м
При
x 0м
,
0 0,0073 рад
x

74.

RА
F
М
А
q
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
При
x 1м
RA 12 q 13
EI EI 0 M 1
2
6
44 103 12 20 103 13
3
3
277,3 10 80 10 1
2
6
( 277,3 80 22 3,3) 103 178,6 103
178,6 103
3
4
,
7
10
рад
7
3,78 10

75.

RА
М
А
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
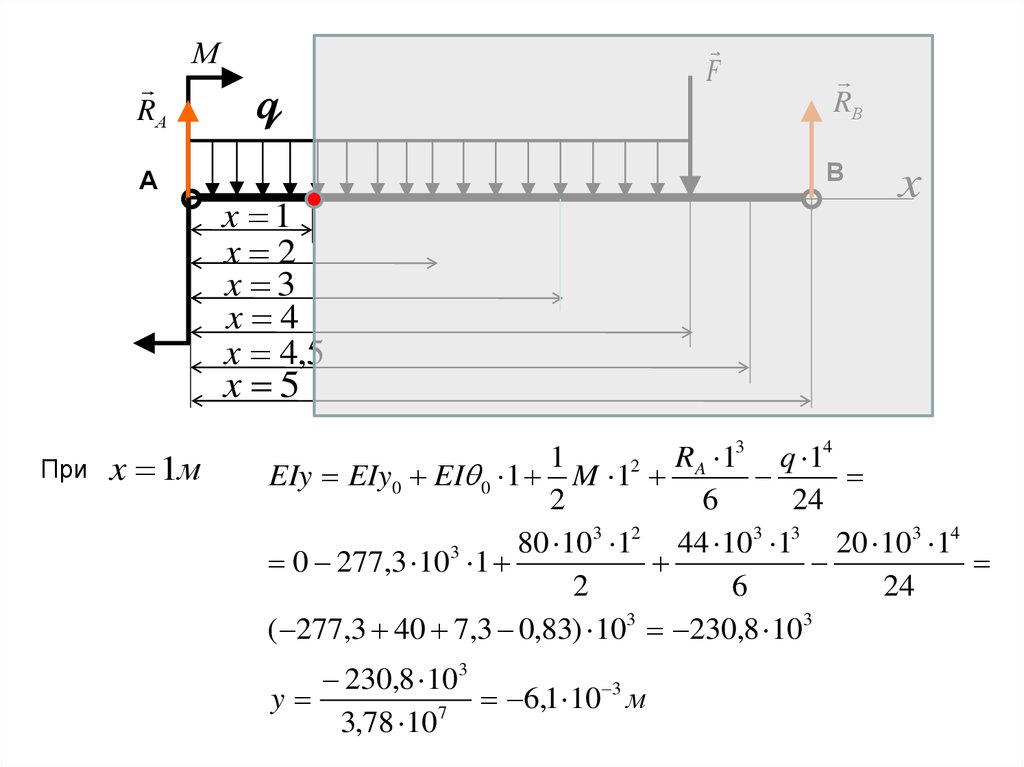
При
x 1м
1
RA 13 q 14
2
EIy EIy0 EI 0 1 M 1
2
6
24
3
2
3
3
3
4
80
10
1
44
10
1
20
10
1
0 277,3 103 1
2
6
24
( 277,3 40 7,3 0,83) 103 230,8 103
230,8 103
3
y
6
,
1
10
м
7
3,78 10

76.

RА
А
М
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
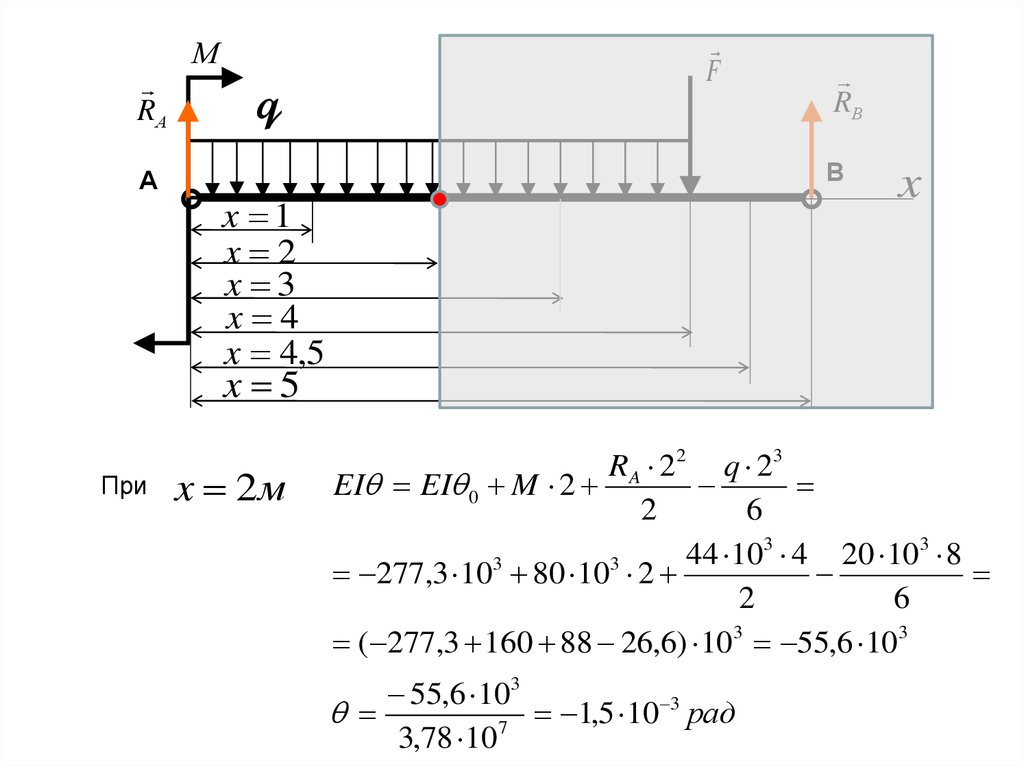
При
x 2м
R A 2 2 q 23
EI EI 0 M 2
2
6
3
3
44
10
4
20
10
8
277,3 103 80 103 2
2
6
( 277,3 160 88 26,6) 103 55,6 103
55,6 103
3
1
,
5
10
рад
7
3,78 10

77.

RА
М
А
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
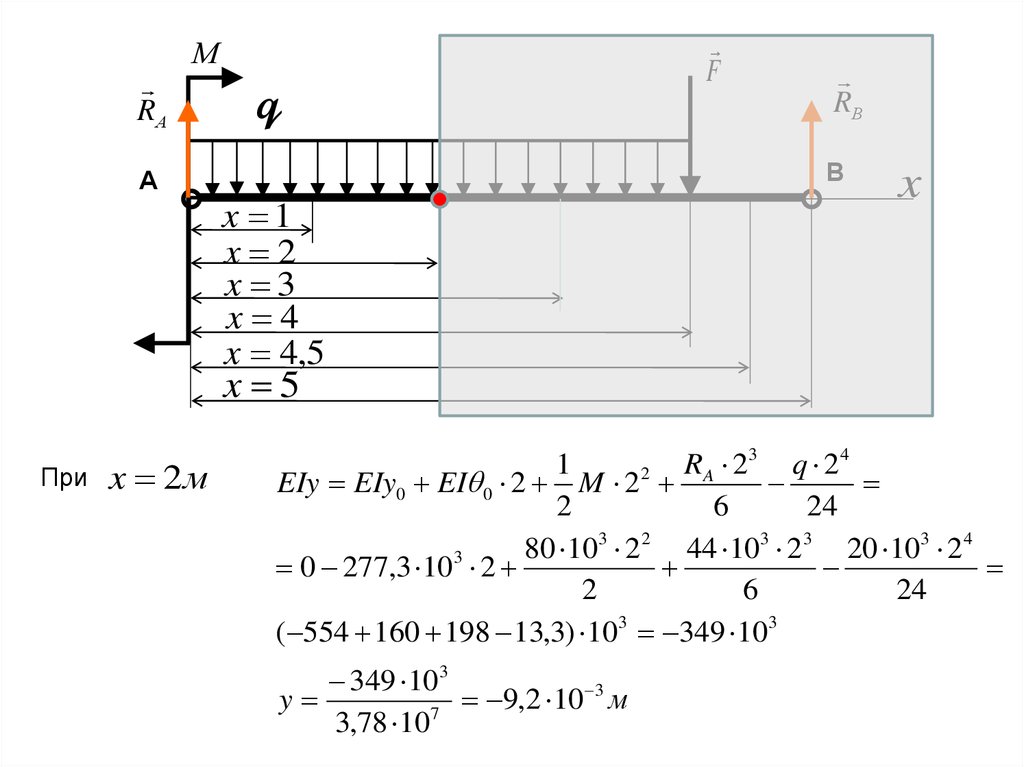
При
x 2м
3
4
1
R
2
q
2
EIy EIy0 EI 0 2 M 2 2 A
2
6
24
80 103 2 2 44 103 23 20 103 2 4
3
0 277,3 10 2
2
6
24
( 554 160 198 13,3) 103 349 103
349 103
3
y
9
,
2
10
м
7
3,78 10

78.

RА
А
М
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
При
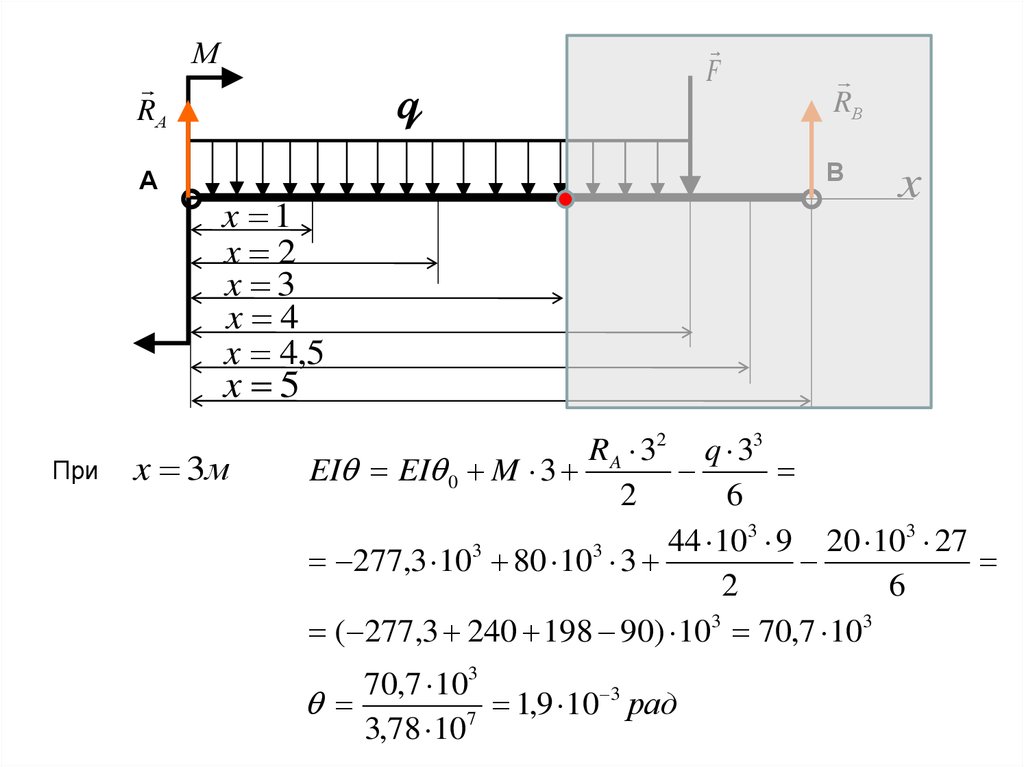
x 3м
RA 32 q 33
EI EI 0 M 3
2
6
44 103 9 20 103 27
3
3
277,3 10 80 10 3
2
6
( 277,3 240 198 90) 103 70,7 103
70,7 103
3
1
,
9
10
рад
7
3,78 10

79.

RА
А
М
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
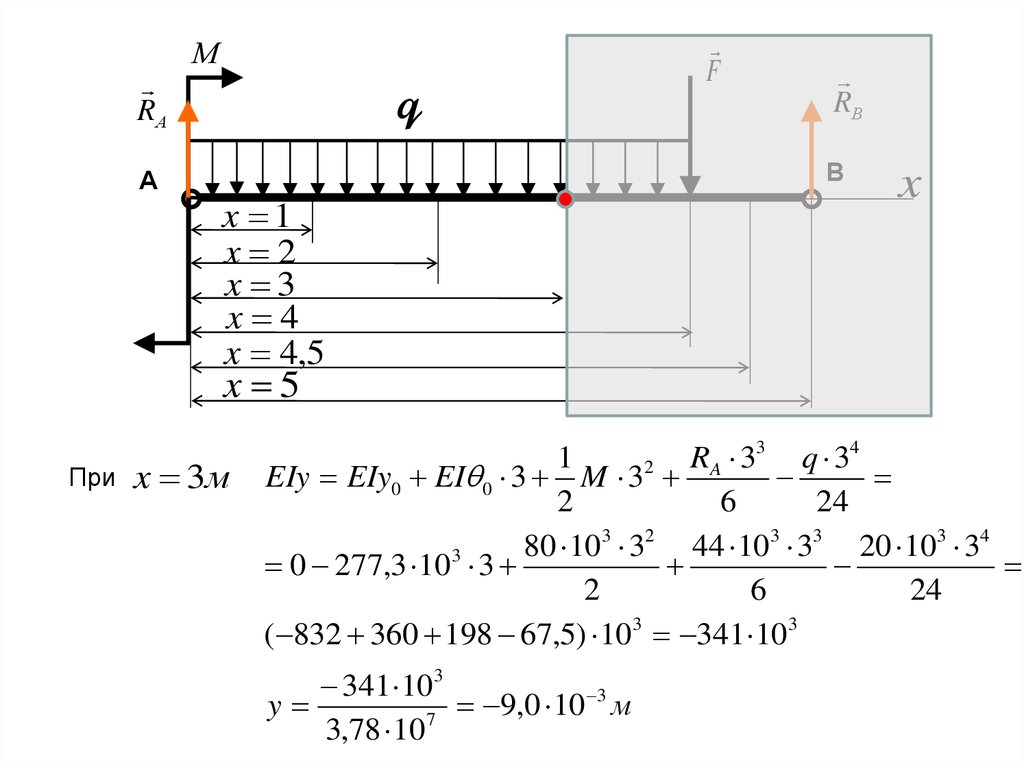
При
x 3м
3
4
1
R
3
q
3
EIy EIy0 EI 0 3 M 32 A
2
6
24
80 103 32 44 103 33 20 103 34
3
0 277,3 10 3
2
6
24
( 832 360 198 67,5) 103 341 103
341 103
3
y
9
,
0
10
м
7
3,78 10

80.

RА
М
А
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
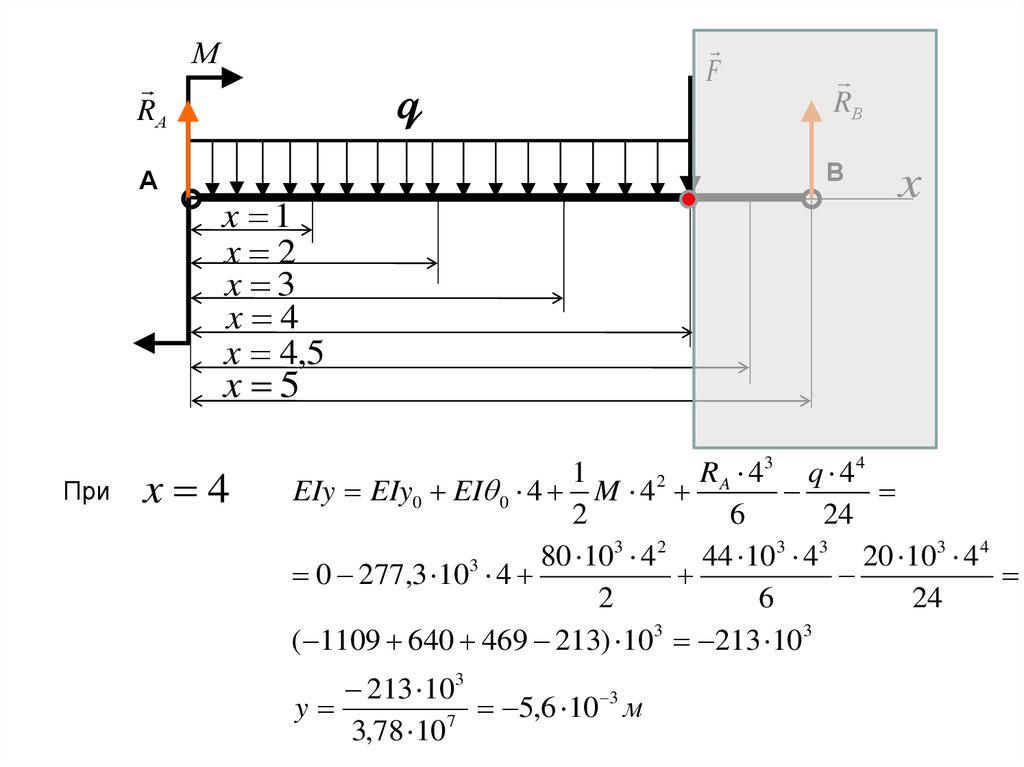
При
x 4
R A 4 2 q 43
EI EI 0 M 4
2
6
44 103 16 20 103 64
3
3
277,3 10 80 10 4
2
6
( 277,3 320 352 213) 103 182 103
182 103
3
4
,
8
10
рад
7
3,78 10

81.

RА
А
М
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
При
x 4
1
R A 43 q 4 4
2
EIy EIy0 EI 0 4 M 4
2
6
24
80 103 4 2 44 103 43 20 103 4 4
3
0 277,3 10 4
2
6
24
( 1109 640 469 213) 103 213 103
213 103
3
y
5
,
6
10
м
7
3,78 10

82.

RА
М
А
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
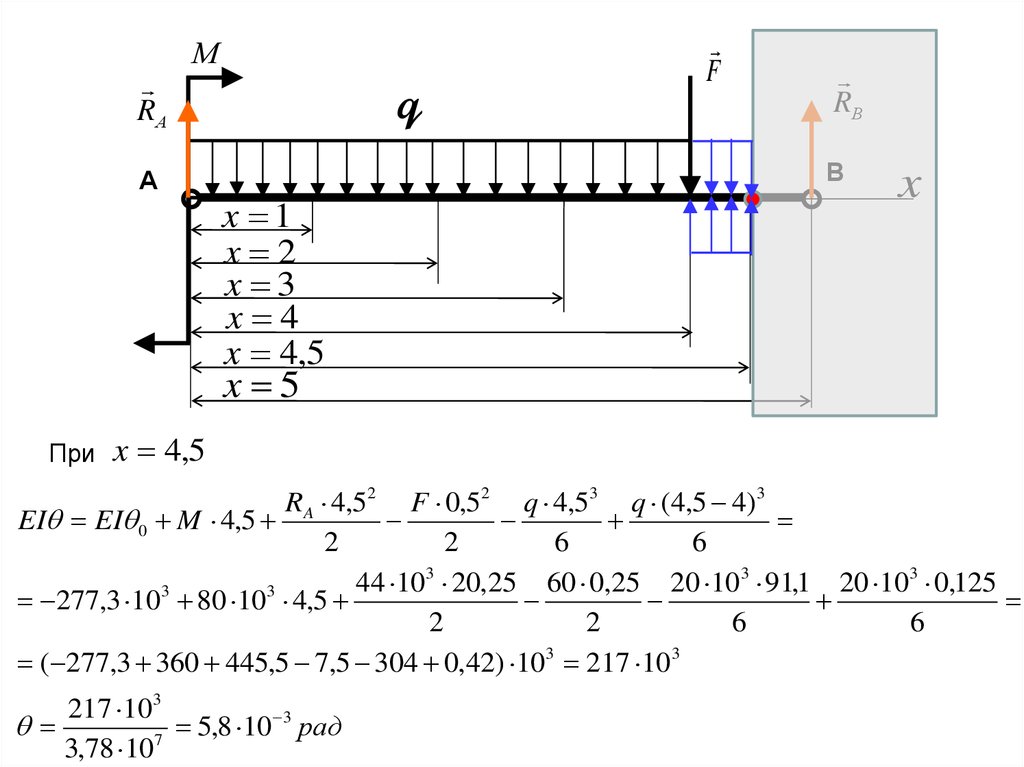
При
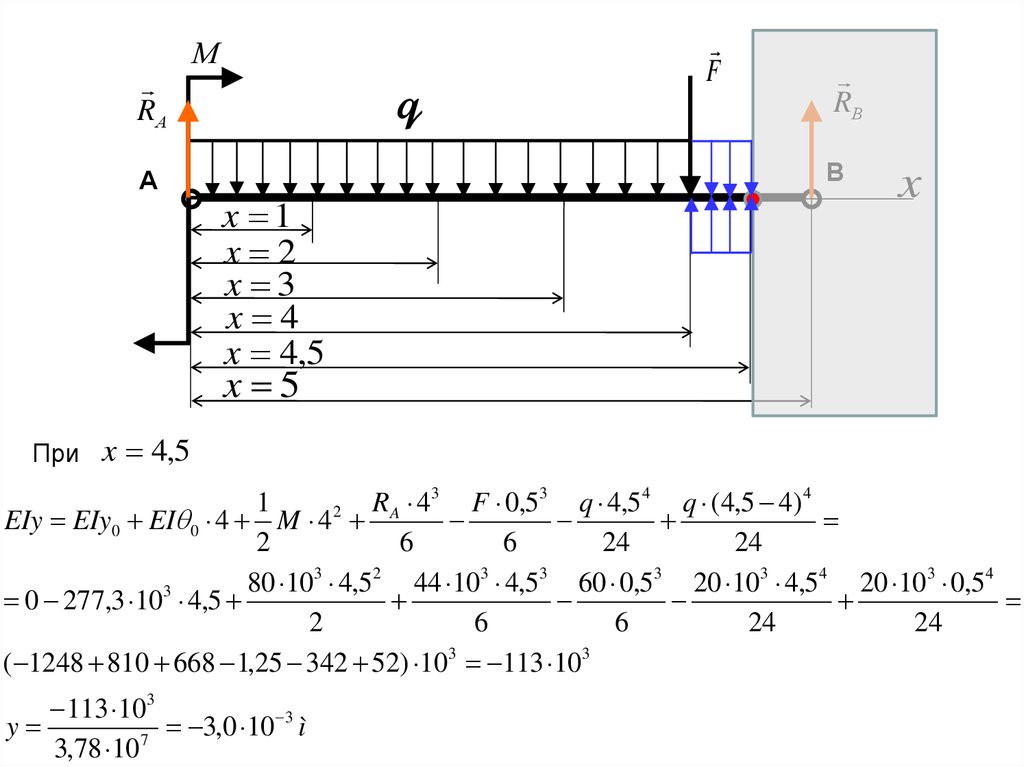
x 4,5
RA 4,52 F 0,52 q 4,53 q (4,5 4) 3
EI EI 0 M 4,5
2
2
6
6
44 103 20,25 60 0,25 20 103 91,1 20 103 0,125
3
3
277,3 10 80 10 4,5
2
2
6
6
( 277,3 360 445,5 7,5 304 0,42) 103 217 103
217 103
3
5
,
8
10
рад
7
3,78 10

83.

RА
А
М
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
При
x 4,5
1
RA 43 F 0,53 q 4,54 q (4,5 4) 4
2
EIy EIy0 EI 0 4 M 4
2
6
6
24
24
80 103 4,52 44 103 4,53 60 0,53 20 103 4,54 20 103 0,54
3
0 277,3 10 4,5
2
6
6
24
24
( 1248 810 668 1,25 342 52) 103 113 103
113 103
3
y
3
,
0
10
ì
7
3,78 10

84.

RА
А
F
М
q
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x
x 5
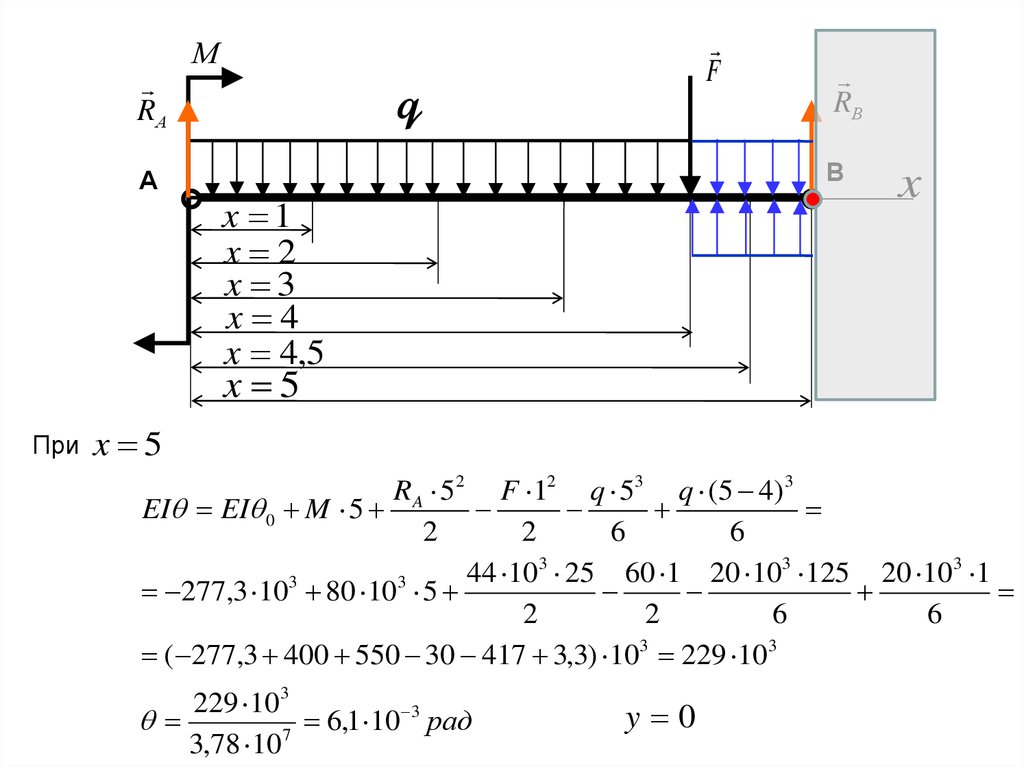
При
x 5
RA 52 F 12 q 53 q (5 4) 3
EI EI 0 M 5
2
2
6
6
3
3
3
44
10
25
60
1
20
10
125
20
10
1
277,3 103 80 103 5
2
2
6
6
( 277,3 400 550 30 417 3,3) 103 229 103
229 103
3
6
,
1
10
рад
7
3,78 10
y 0

85.

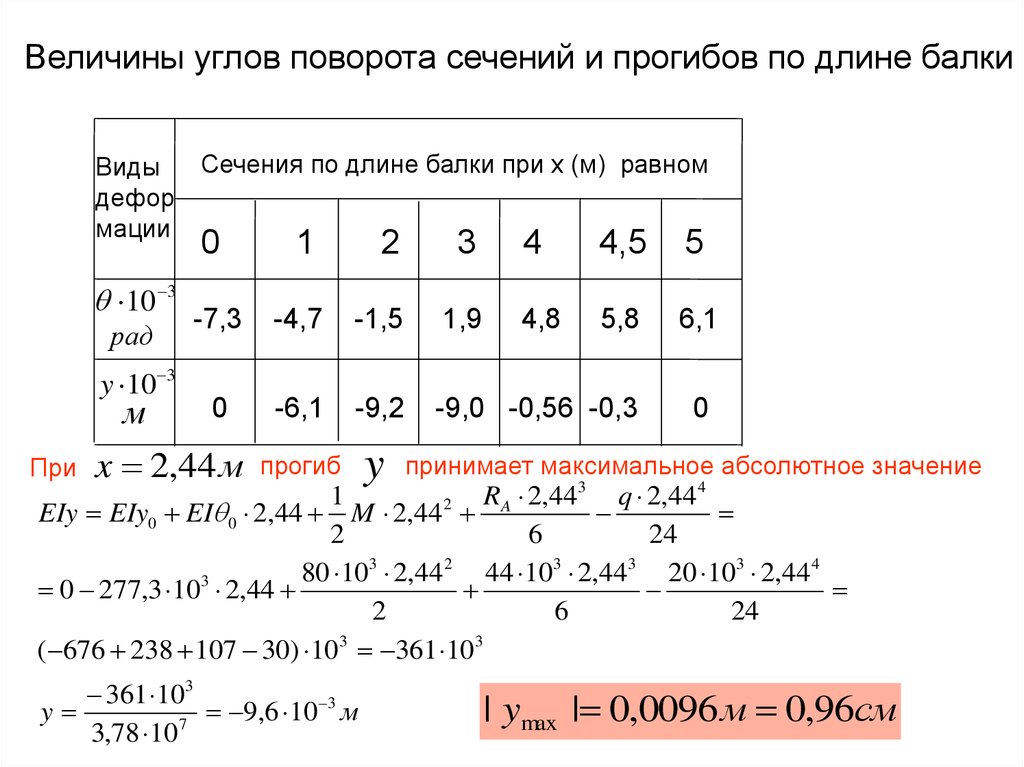
Величины углов поворота сечений и прогибов по длине балки
Виды
дефор
мации
0
1
2
3
4
4,5
5
-7,3
-4,7
-1,5
1,9
4,8
5,8
6,1
0
м
x 2,44 м
-6,1
-9,2
-9,0 -0,56 -0,3
прогиб
y
10 3
рад
y 10 3
При
Сечения по длине балки при х (м) равном
0
принимает максимальное абсолютное значение
1
RA 2,443 q 2,44 4
2
EIy EIy0 EI 0 2,44 M 2,44
2
6
24
80 103 2,44 2 44 103 2,443 20 103 2,44 4
3
0 277,3 10 2,44
2
6
24
( 676 238 107 30) 103 361 103
361 103
3
y
9
,
6
10
м
7
3,78 10
| ymax | 0,0096 м 0,96см

86.

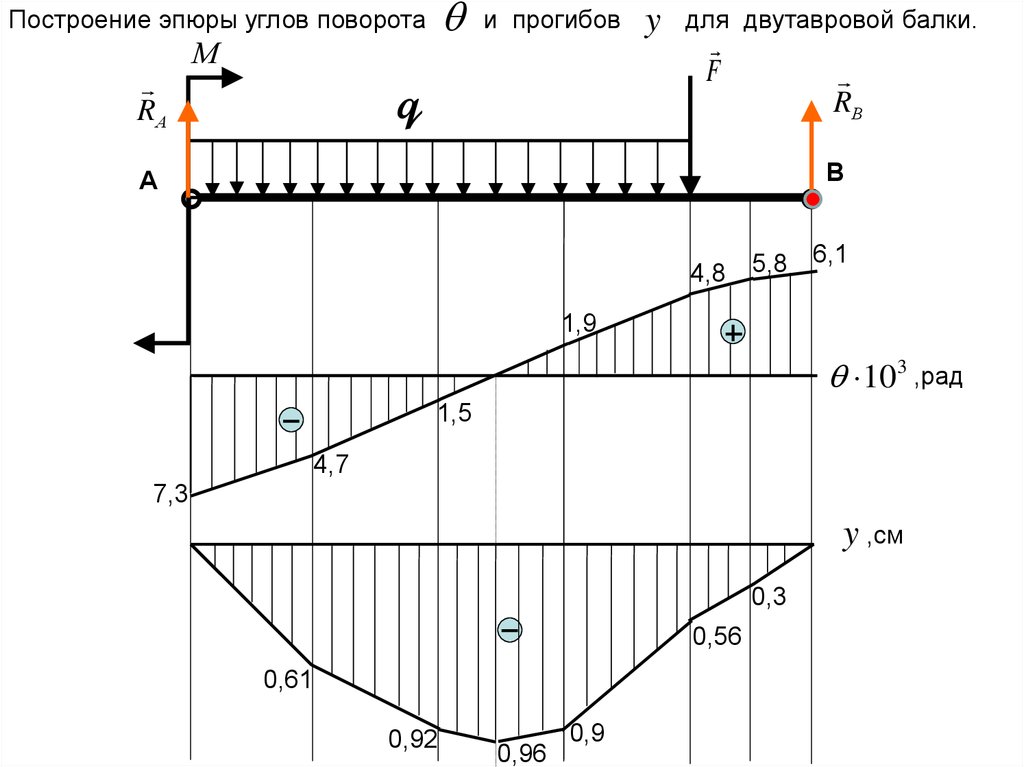
Построение эпюры углов поворота
RА
М
и прогибов
q
y
для двутавровой балки.
F
RВ
В
А
4,8
5,8 6,1
1,9
103 ,рад
1,5
4,7
7,3
y ,см
0,3
0,56
0,61
0,92
0,96
0,9

87.

8) Проверка двутавровой балки на жесткость.
Для проверки двутавровой балки на жесткость используется условие:
ymax y
Допускаемое значение прогиба для однопролетной балки в опасном сечении
l
5
y
0,016 м
300 300
Балка имеет максимальный прогиб в сечении, где х = 2,44 м.
| ymax | 0,0096 м
0,0096 0,016
Условие выполняется

88.

RА
М
q
F
RВ
В
А
l₁
l₂

89.

F
М
В
А
l₁
l₂

90.

RА
А
М
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x 5
x

91.

F
q
М
В
А
2,2 м
44
+
36
-
Q
(кН)
119,6
96
96
80
+
М (кН• м)

92.

x 5
RА
А
М
q
F
RВ
В
x 1
x 2
x 3
x 4
x 4,5
x 5
x

93.

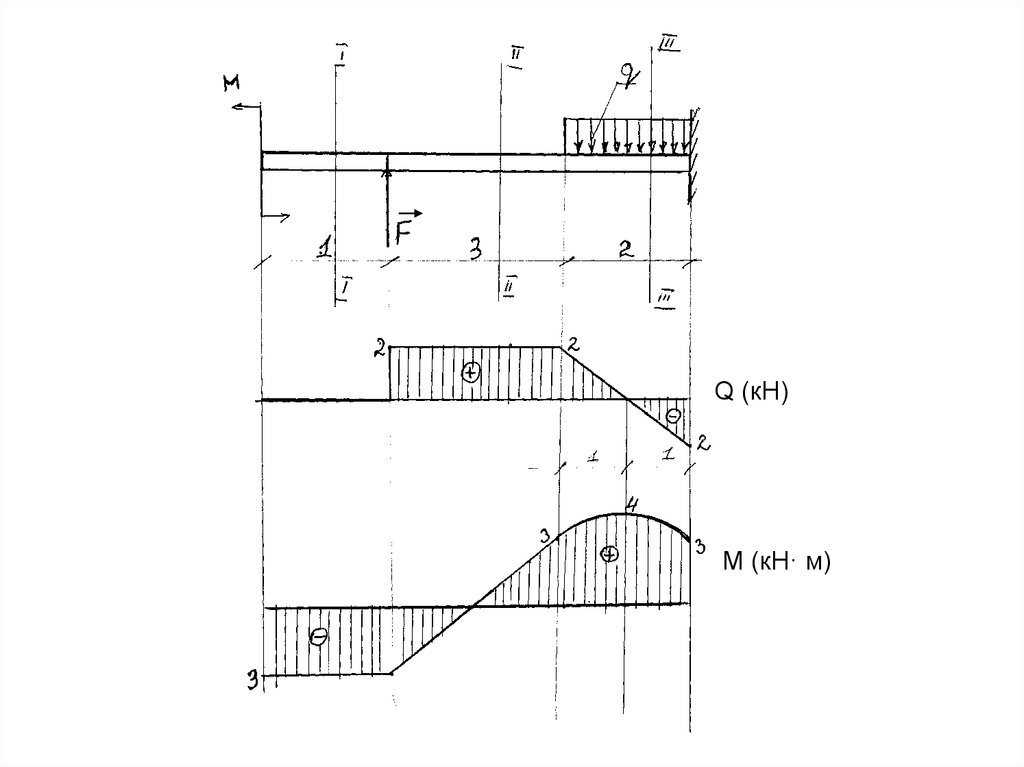
Q (кН)
М (кН· м)

94.

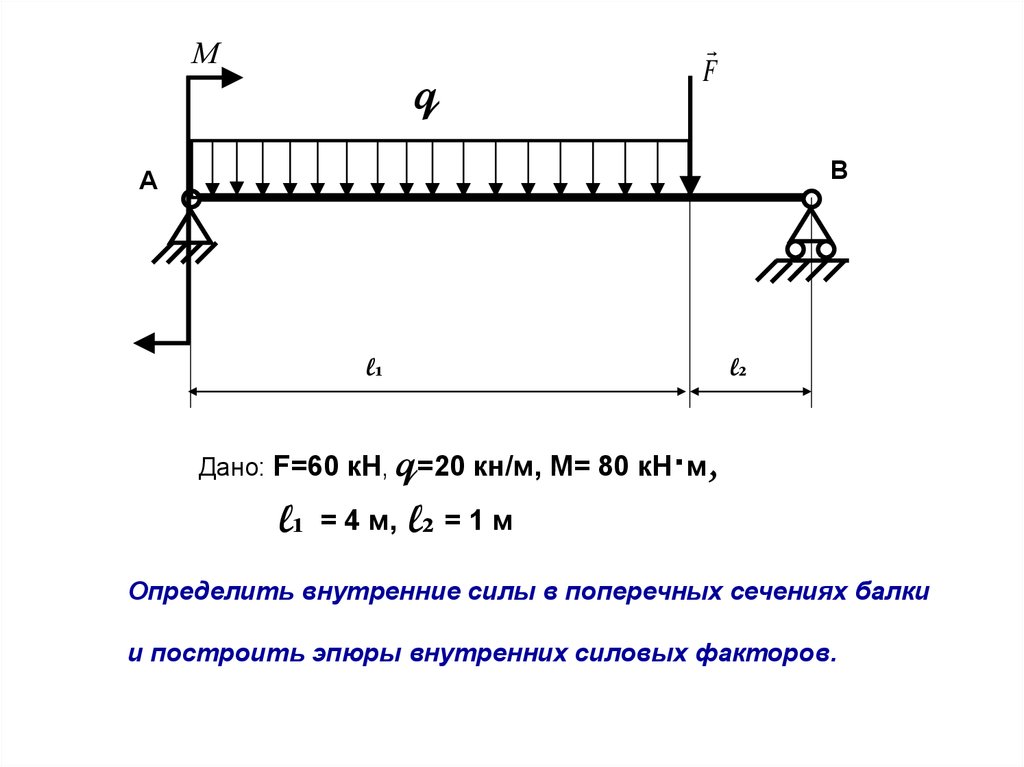
М
q
F
В
А
l₁
l₂
Дано: F=60 кН, q=20 кн/м, М= 80 кН·м,
l₁
= 4 м,
l₂ = 1 м
Определить внутренние силы в поперечных сечениях балки
и построить эпюры внутренних силовых факторов.