Равнобедренный треугольник и его свойства

1.

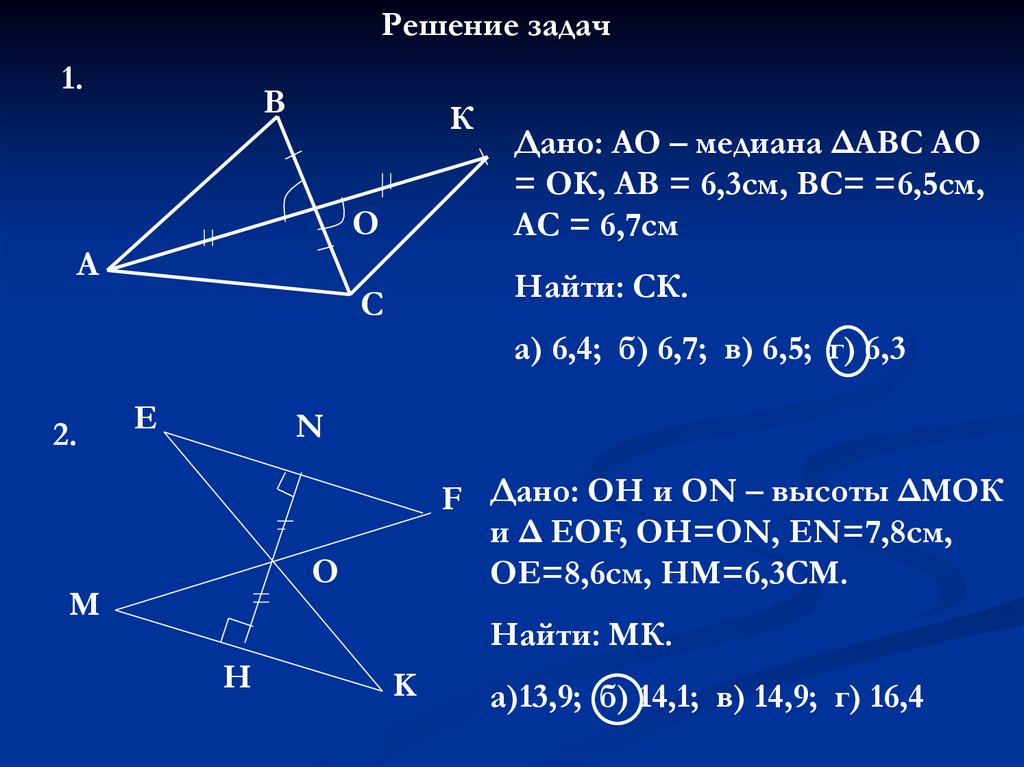
Решение задач
1.
В
К
О
А
Дано: АО – медиана ΔАВС АО
= ОК, АВ = 6,3см, ВС= =6,5см,
АС = 6,7см
Найти: СК.
С
а) 6,4; б) 6,7; в) 6,5; г) 6,3
2.
Е
N
F Дано: ОН и ОN – высоты ΔМОК
и Δ ЕОF, OH=ON, EN=7,8см,
ОЕ=8,6см, НМ=6,3СМ.
О
M
Найти: МК.
H
K
а)13,9; б) 14,1; в) 14,9; г) 16,4

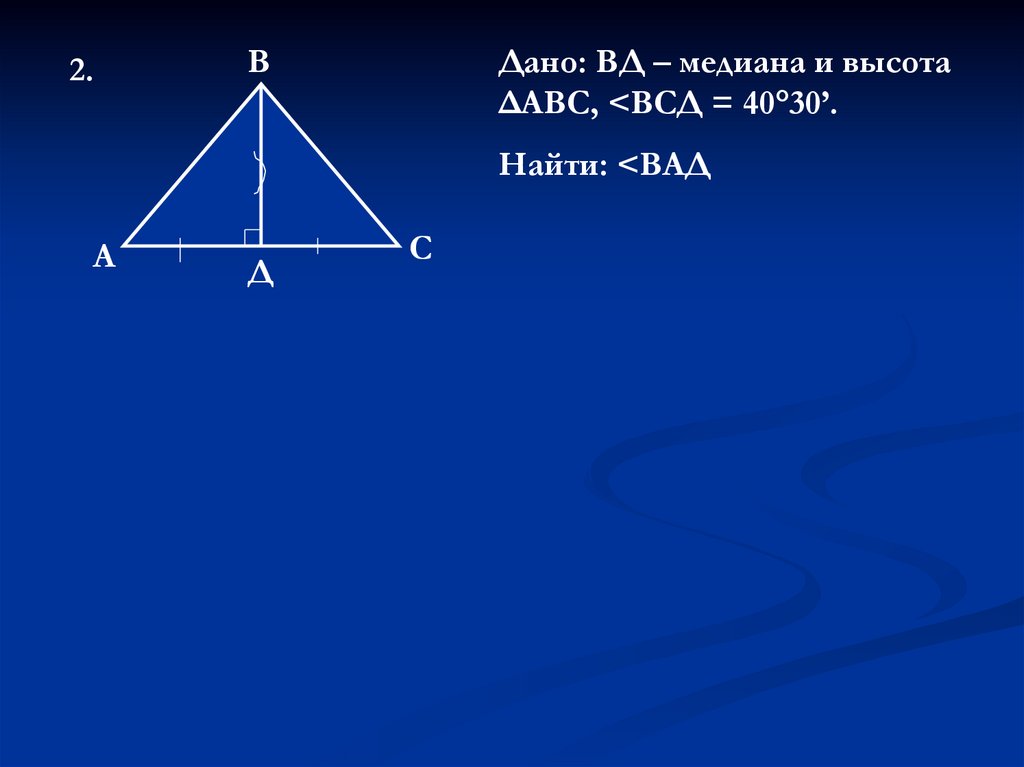
2.

2.
В
Дано: ВД – медиана и высота
ΔАВС, <ВСД = 40°30’.
Найти: <ВАД
А
Д
С

3.

О
О
О

4.

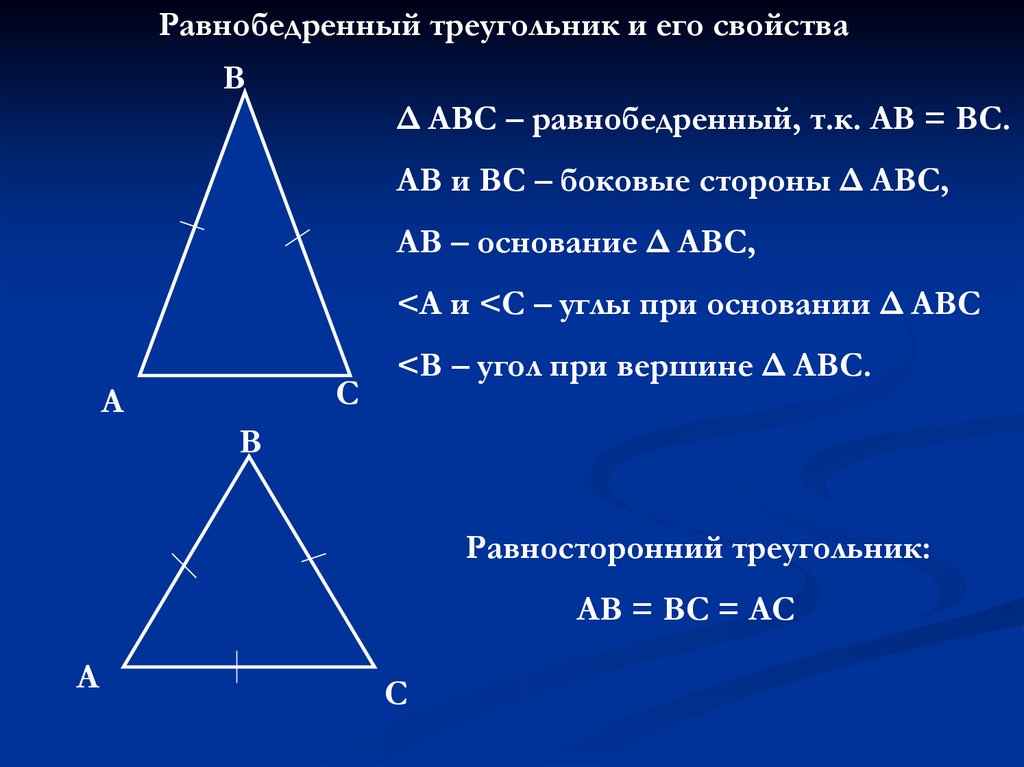
Равнобедренный треугольник и его свойства
В
Δ АВС – равнобедренный, т.к. АВ = ВС.
АВ и ВС – боковые стороны Δ АВС,
АВ – основание Δ АВС,
<А и <С – углы при основании Δ АВС
С
А
<В – угол при вершине Δ АВС.
В
Равносторонний треугольник:
АВ = ВС = АС
А
С

5.

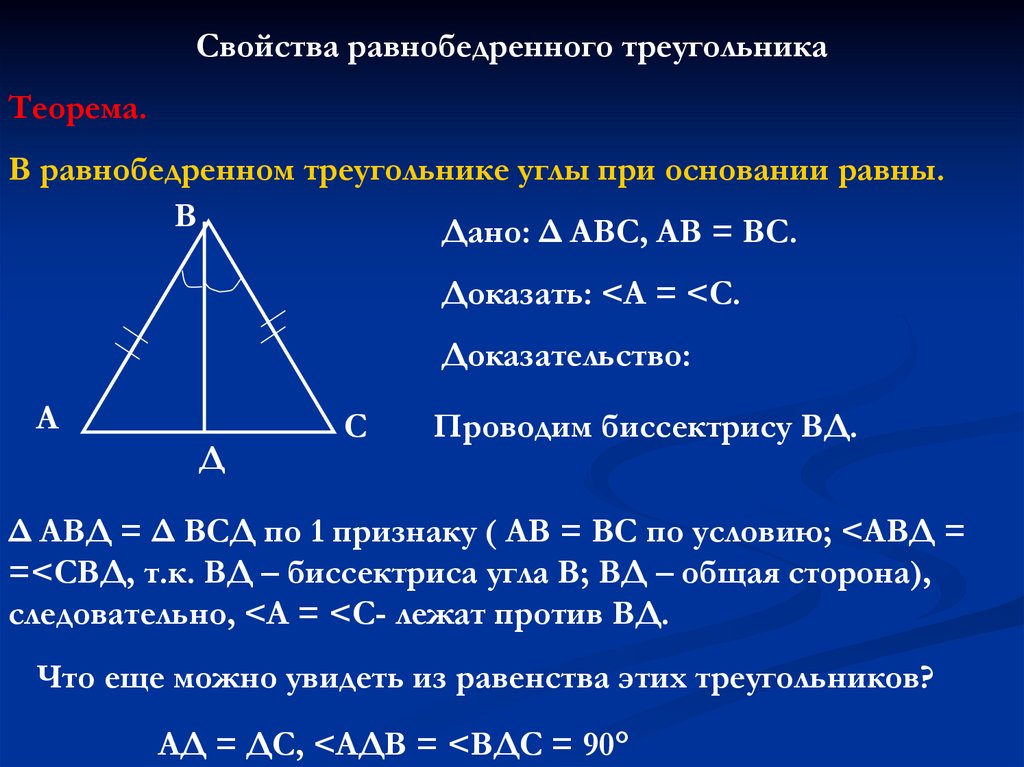
Свойства равнобедренного треугольника
Теорема.
В равнобедренном треугольнике углы при основании равны.
В
Дано: Δ АВС, АВ = ВС.
Доказать: <А = <С.
Доказательство:
А
Д
С
Проводим биссектрису ВД.
Δ АВД = Δ ВСД по 1 признаку ( АВ = ВС по условию; <АВД =
=<СВД, т.к. ВД – биссектриса угла В; ВД – общая сторона),
следовательно, <А = <С- лежат против ВД.
Что еще можно увидеть из равенства этих треугольников?
АД = ДС, <АДВ = <ВДС = 90°

6.

В равнобедренном треугольнике биссектриса, проведенная из
угла при вершине, является медианой и высотой.
Можно ли сказать это о любой биссектрисе?
Что можно сказать о медиане равнобедренного треугольника,
проведенной к его основанию?
О высоте, проведенной к основанию?
Любая медиана является высотой и биссектрисой в
равнобедренном треугольнике?
А высота?

7.

Д/з. § 18, вопросы 10 – 13.
№ 108, 110, 112.
№ 109,
107 (самостоятельно).