Соотношения между сторонами и углами в прямоугольном треугольнике

1.

Соотношения
между сторонами и углами
в прямоугольном треугольнике

2.

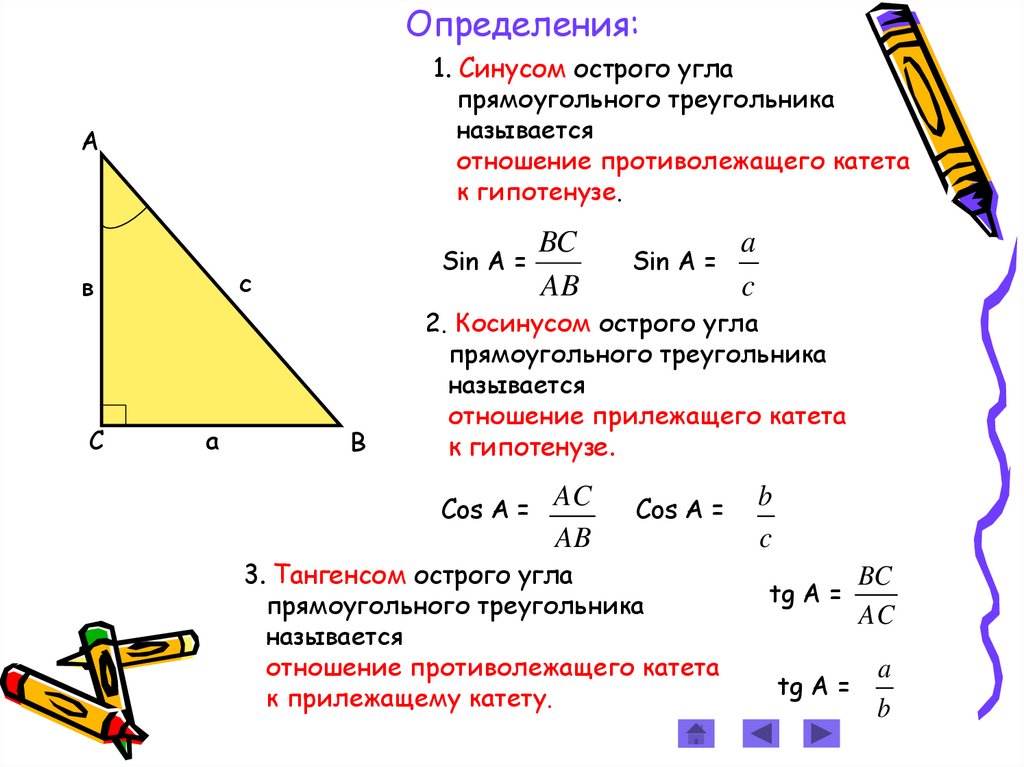
Определения:
1. Синусом острого угла
прямоугольного треугольника
называется
отношение противолежащего катета
к гипотенузе.
А
с
в
С
Sin A =
а
В
BC
AB
Sin A =
a
c
2. Косинусом острого угла
прямоугольного треугольника
называется
отношение прилежащего катета
к гипотенузе.
Cos A =
AC
AB
Cos A =
3. Тангенсом острого угла
прямоугольного треугольника
называется
отношение противолежащего катета
к прилежащему катету.
b
c
tg A =
BC
AC
a
tg A =
b

3.

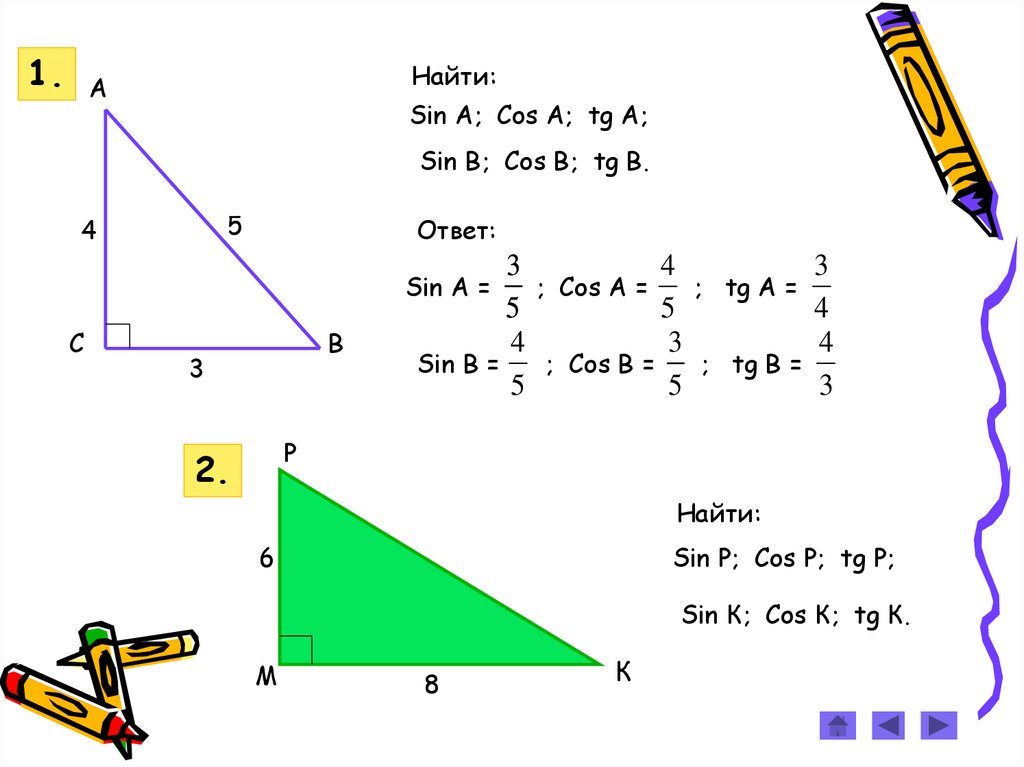
1.
Найти:
A
Sin A; Cos A; tg A;
Sin В; Cos В; tg В.
5
4
C
Ответ:
B
3
3
4
Sin A =
; Cos A =
; tg A =
5
5
4
3
Sin В =
; Cos В =
; tg В =
5
5
3
4
4
3
Р
2.
Найти:
Sin Р; Cos Р; tg Р;
6
Sin К; Cos К; tg К.
М
8
К

4.

Тест
В
1.
А
Дано: АВСК – прямоугольник,
С
Cos = 0.5, тогда Cos = …….
Ответ: а)
К
1
2
б) 2
а)
2.
В
К
в) 0,25
1
2
М
Найти: Sin Р.
4
Ответ: а) 0,8
5
Р
С
А
б) 0,6
б) 0,6
в) 0,75

5.

3.
Найти синус, косинус и тангенс острых углов
по данным на чертеже:
А
17 см
С
15 см
В

6.

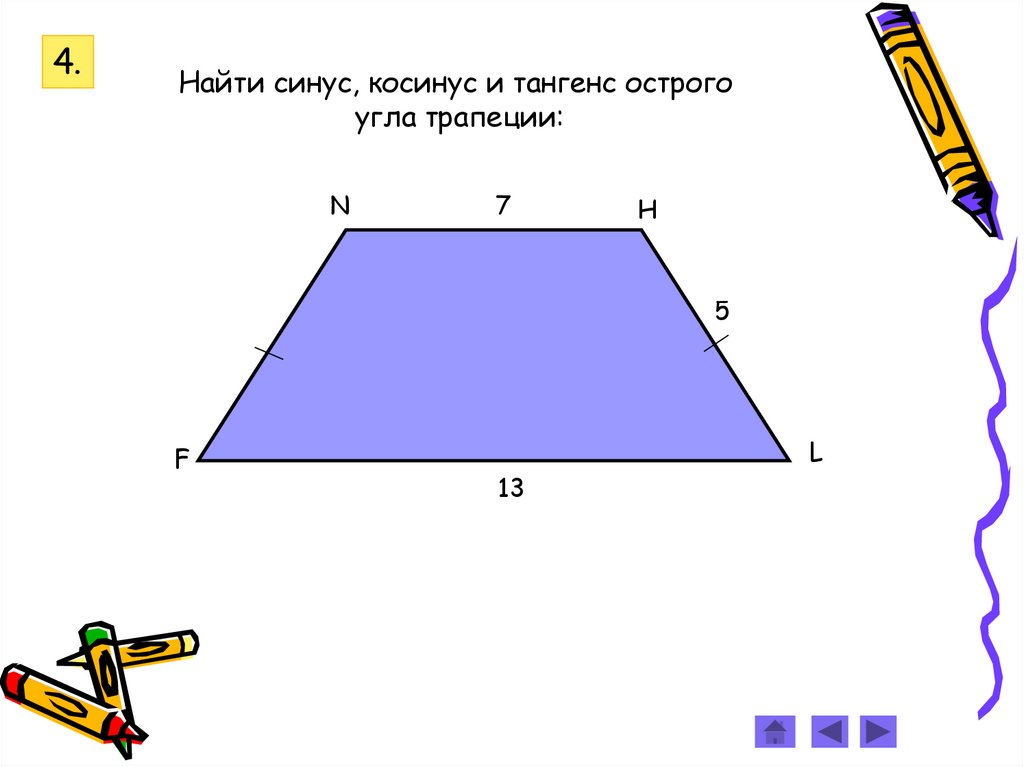
4.
Найти синус, косинус и тангенс острого
угла трапеции:
N
7
H
5
F
L
13

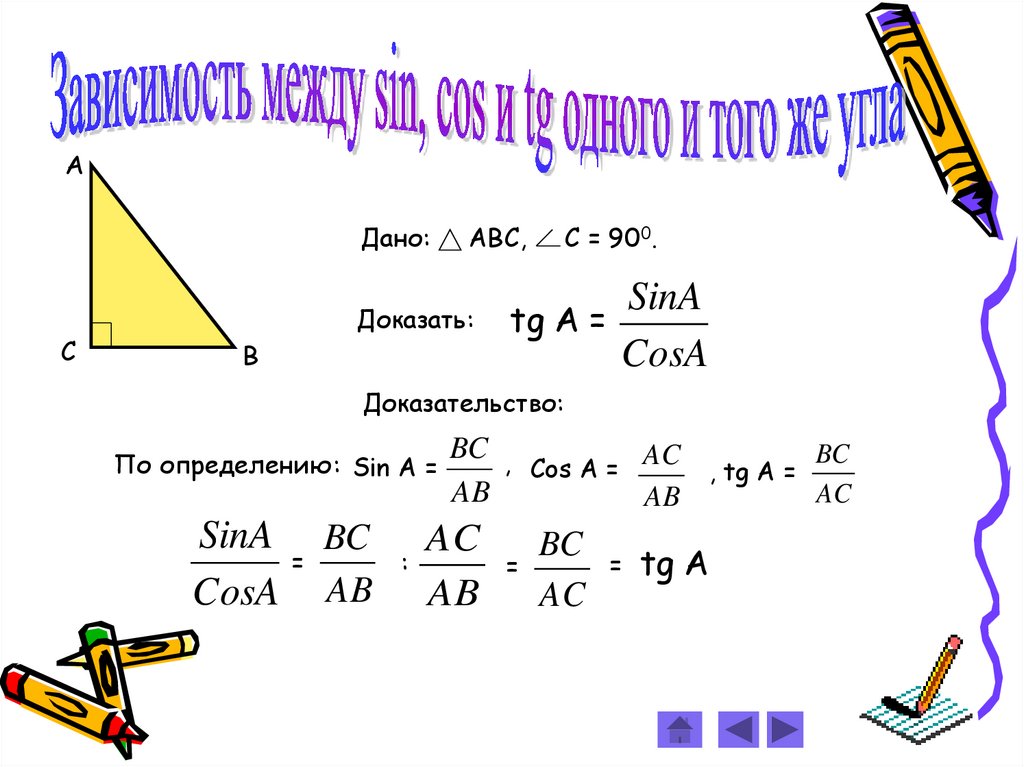
7.

А
Дано:
АВС,
С = 900.
Доказать: Sin2A
С
+ Cos2A = 1
Доказательство:
В
По определению Sin A =
2
BC
BC
, значит, Sin2 A =
AB
AB 2
2
AC
AC
2
По определению Cos A =
, значит, Cos A =
2
AB
AB
2
2
2
2
2
BC
AC
BC
AC
AB
2
2
Sin A + Cos A =
1
2 +
2 =
2
2
AB
AB
AB
AB
Следовательно, Sin2A + Cos2A = 1

8.

А
Дано:
С
АВС,
Доказать:
В
С = 900.
SinA
tg A =
CosA
Доказательство:
По определению: Sin A =
SinA
CosA
=
BC
AB
:
BC ,
BC
AC
Cos A =
, tg A =
AB
AC
AB
AC
AB
=
BC
AC
=
tg A

9.

2
sin a
+
Sin2a = 1 – cos2a
Sin a = √1 – cos2a
2
cos a
=1
Cos2a = 1 – sin2a
Cos a = √1 – sin2a
SinA
tg A =
CosA

10.

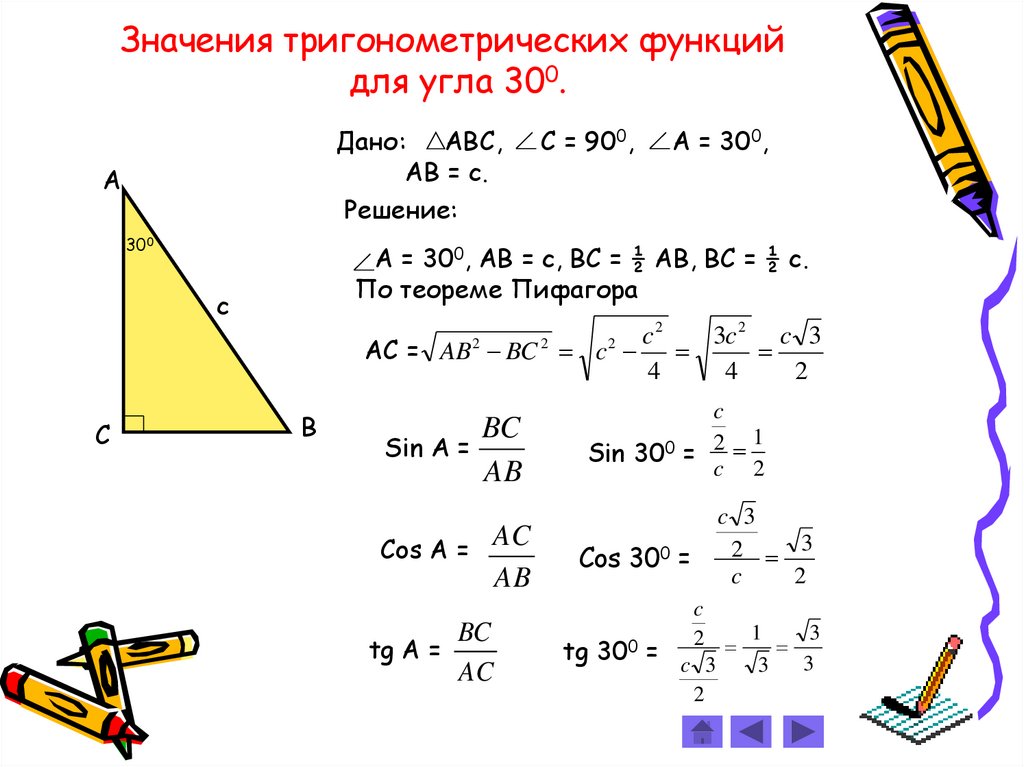
Значения тригонометрических функций
для углa 300.
Дано: АВС,
АВ = с.
Решение:
А
300
С = 900,
А = 300,
А = 300, АВ = с, ВС = ½ АВ, ВС = ½ с.
По теореме Пифагора
с
c2
3c 2 c 3
АС = AB BC c
4
4
2
2
С
В
BC
Sin A =
AB
AC
Cos A =
AB
tg A =
BC
AC
2
2
c
1
Sin 300 = 2
c 2
Cos 300 =
tg 300 =
c 3
2 3
c
2
c
2 1 3
3
c 3
3
2

11.

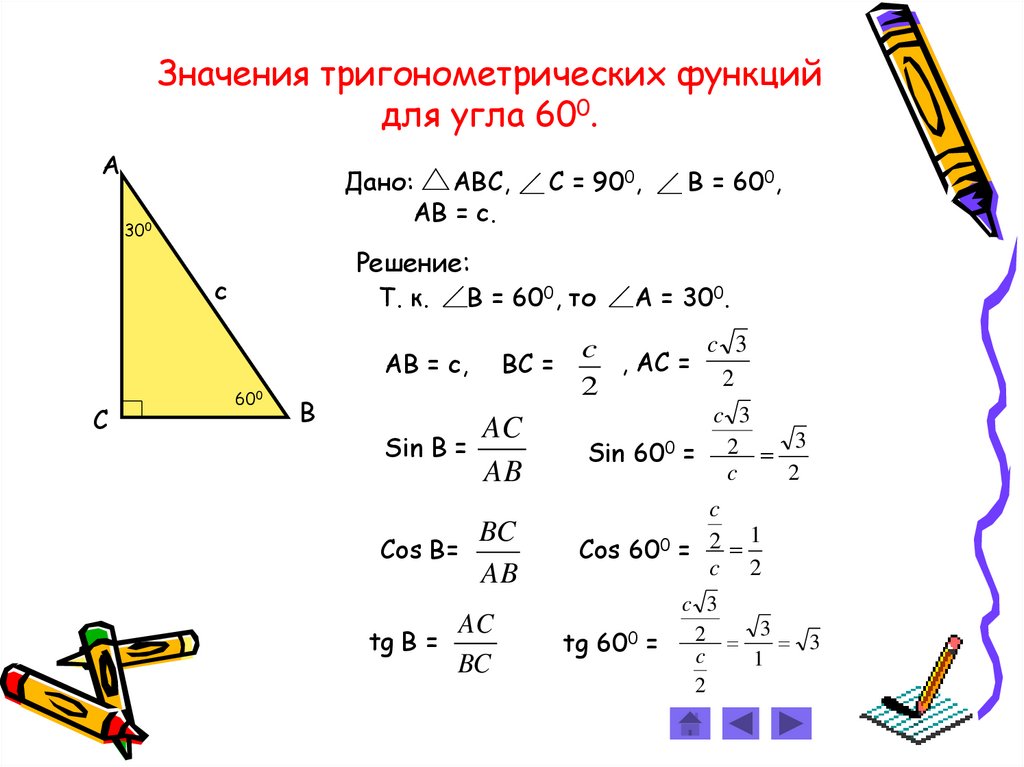
Значения тригонометрических функций
для углa 600.
А
Дано: АВС,
АВ = с.
300
Решение:
Т. к. В = 600, то
с
600
В
AC
Sin В =
AB
Cos В=
tg В =
B = 600,
А = 300.
c 3
c
, АС =
ВС =
2
2
АВ = с,
С
С = 900,
BC
AB
AC
BC
c 3
3
Sin 600 = 2
c
2
c
1
Cos 600 = 2
c 2
tg 600 =
c 3
2 3 3
c
1
2

12.

Значения тригонометрических функций
для углa 450.
Дано: АВС,
АВ = с.
А
450
С = 900,
А = 450,
Решение:
Т. к.
с
А = 450, то
В = 450.
Значит,
АВС – равнобедренный,
следовательно, АС = ВС = х.
С
450
В
По теореме Пифагора: х2 +х2 =с2, 2х2 = с2,
х2 =
BC
Sin A =
AB
c2
2
,х=
c 2
c 2
, АС = ВС =
2
2
c 2
2 , Cos450 =
Sin 450 = 2
c
2
tg 450 = 1
2
2

13.

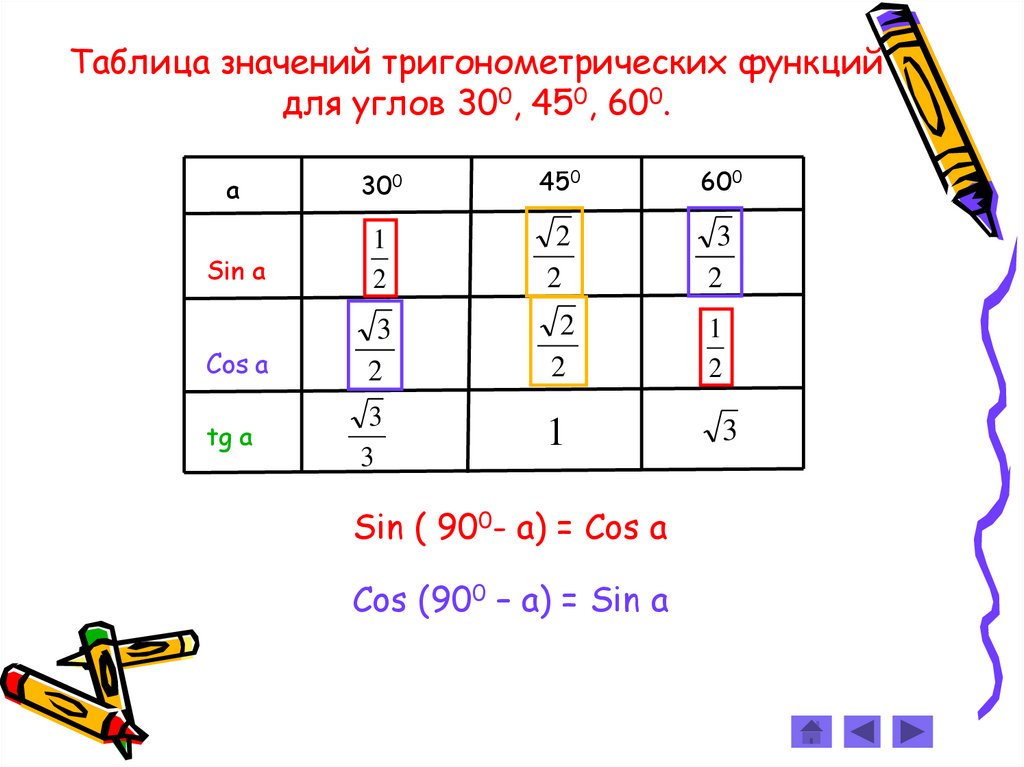
Таблица значений тригонометрических функций
для углов 300, 450, 600.
a
300
450
600
Sin a
1
2
2
2
3
2
Cos a
3
2
2
2
1
2
tg a
3
3
1
Sin ( 900- a) = Cos a
Cos (900 – a) = Sin a
3

14.

Проверь своё внимание и память :
Для какого из углов неправильно указано в таблице
значение одной из тригонометрических функций?
И какой ?
a
Sin a
Cos a
300
1
2
3
2
3
450
2
2
2
2
1
600
3
2
1
2
Неправильно указан tg300
tg a
3

15.

Решение прямоугольных треугольников
a
Sin
c
с
b
b
Cos
c
а
a c Sin
a
c
Sin
b c Cos
b
c
Cos
a b tg
a
tg
b
a
b
tg

16.

1.
Реши задачу
Найти углы, которые образует диагональ прямоугольника
с его сторонами, если стороны прямоугольника равны
3 дм и 1 дм.
С
В
1
А
3
300, 600.
К

17.

Реши задачу
2.
Найти катеты прямоугольного треугольника:
А
600
4
AC 2, BC 2 3
В
С
3.
Найти площадь параллелограмма:
2
600
6
6 3

18.

Ист ория названий
Линия синуса у индийских математиков первоначально
называлась «арха-джива» («полутетива», то есть половина хорды),
затем слово «арха» было отброшено и линию синуса стали
называть просто «джива».
Арабские переводчики стали называть линию синуса «джиба».
Затем арабы стали произносить название линии синуса «джайб»,
что буквально обозначает «впадина», «пазуха».
При переводе арабских сочинений на латынь европейские переводчики
перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современные краткие обозначения sin и cos введены Уильямом Отредом
и закреплены в трудах Эйлера.
Термин «тангенс» (от лат. tangens — касающийся) введен
датским математиком Томасом Финке
(1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.

19.

Михайлова Л. П.
ГОУ ЦО № 173.