Задачи. Куб, тетраэдр

1.

ЗАДАЧА № 1
Докажите, что можно выбрать 4 вершины куба так,
что они будут вершинами правильного тетраэдра.
Ответ
В1
В1
С1
D1
A1
С1
D1
A1
в)
а)
В
А
AB1D1C
В
С
D
А
С
D
A1C1DB
далее

2.

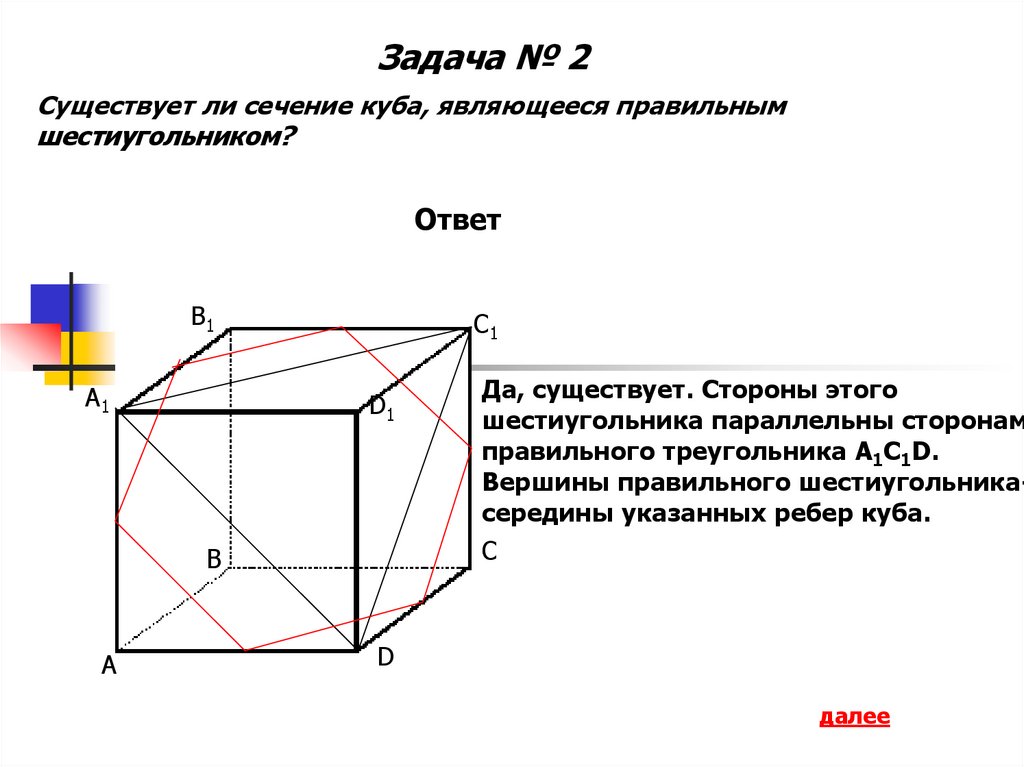
Задача № 2
Существует ли сечение куба, являющееся правильным
шестиугольником?
Ответ
B1
A1
C1
D1
B
A
Да, существует. Стороны этого
шестиугольника параллельны сторонам
правильного треугольника A1C1D.
Вершины правильного шестиугольникасередины указанных ребер куба.
C
D
далее

3.

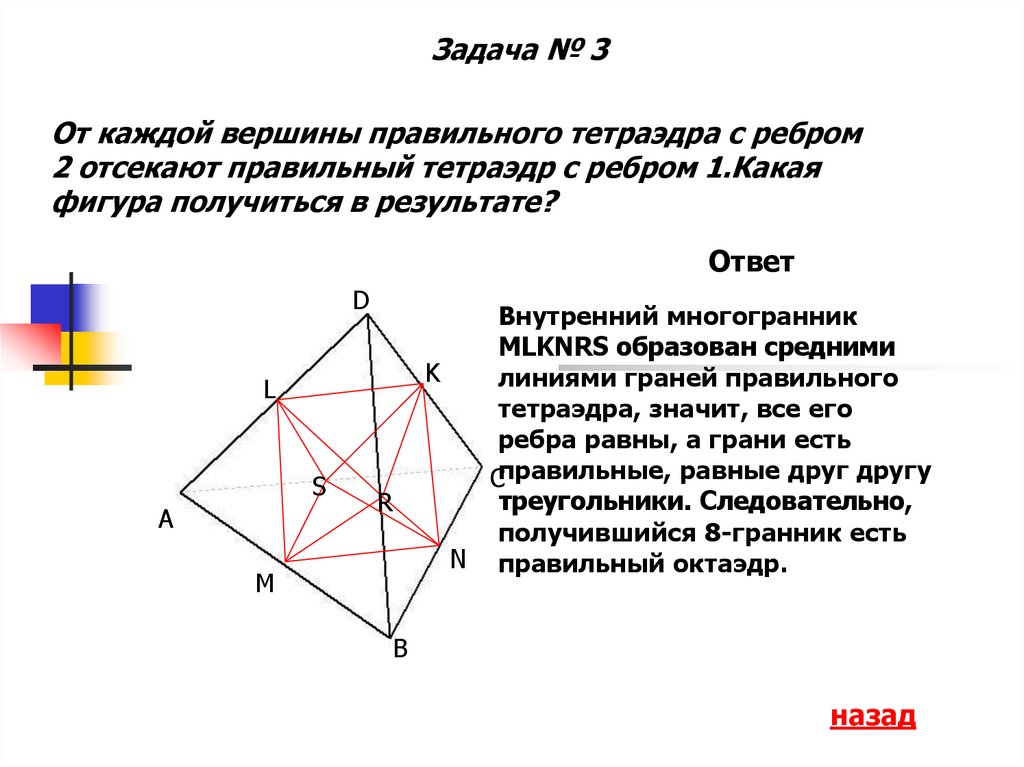
Задача № 3
От каждой вершины правильного тетраэдра с ребром
2 отсекают правильный тетраэдр с ребром 1.Какая
фигура получиться в результате?
Ответ
D
Внутренний многогранник
MLKNRS образован средними
K
линиями граней правильного
тетраэдра, значит, все его
ребра равны, а грани есть
Cправильные, равные друг другу
треугольники. Следовательно,
получившийся 8-гранник есть
N правильный октаэдр.
L
S
A
R
M
B
назад