Правильная четырехугольная пирамида. Задача. Подготовка к ЕГЭ С2

1. Подготовка к ЕГЭ

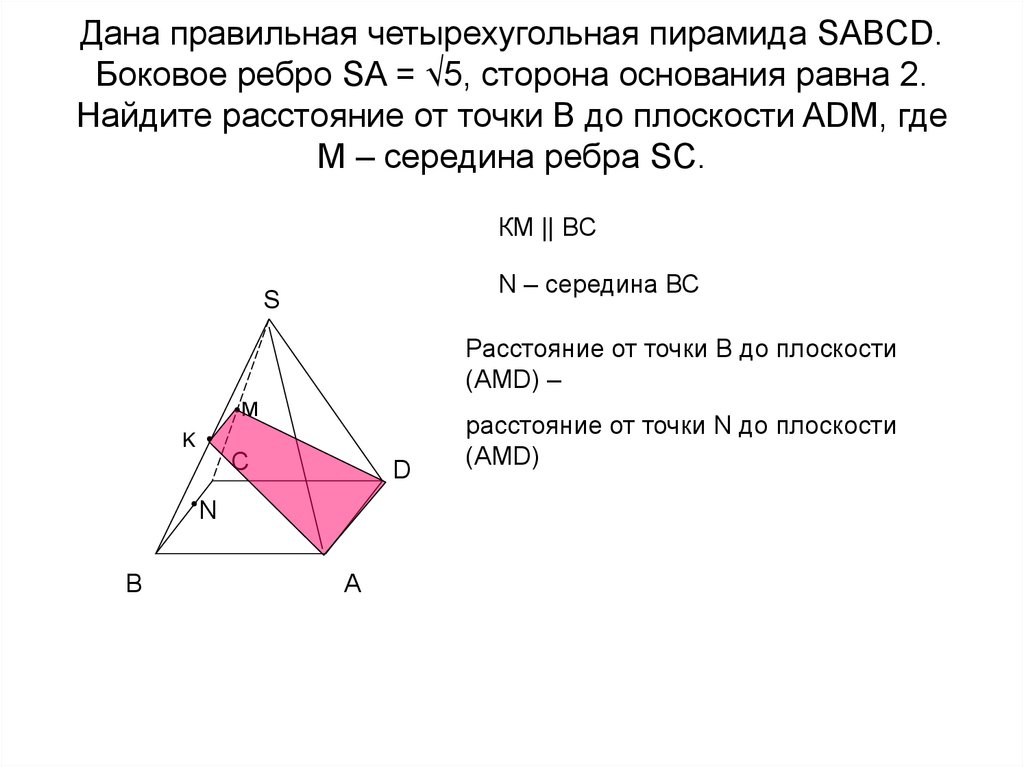
С2

2. Дана правильная четырехугольная пирамида SABCD. Боковое ребро SA = √5, сторона основания равна 2. Найдите расстояние от точки В

до плоскости ADM, где
М – середина ребра SC.
КМ || ВС
N – середина ВС
S
Расстояние от точки В до плоскости
(AMD) –
M
K
С
D
N
В
А
расстояние от точки N до плоскости
(АМD)

3.

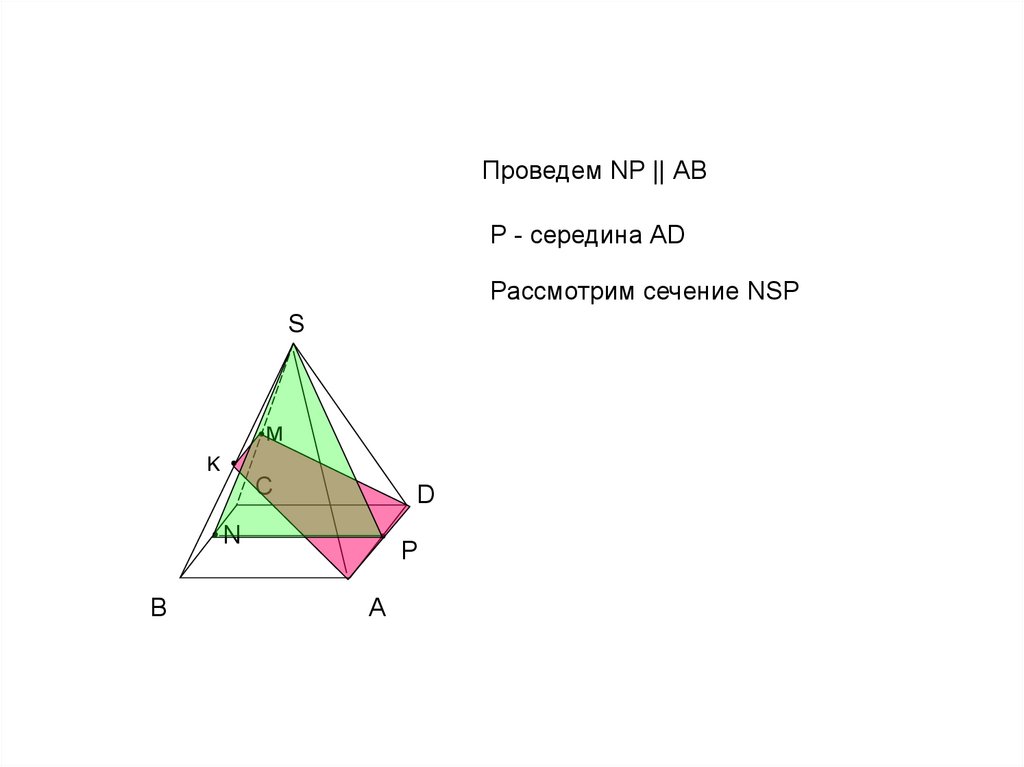
Проведем NP || АВ
P - середина АD
Рассмотрим сечение NSP
S
M
K
С
D
N
В
P
А

4.

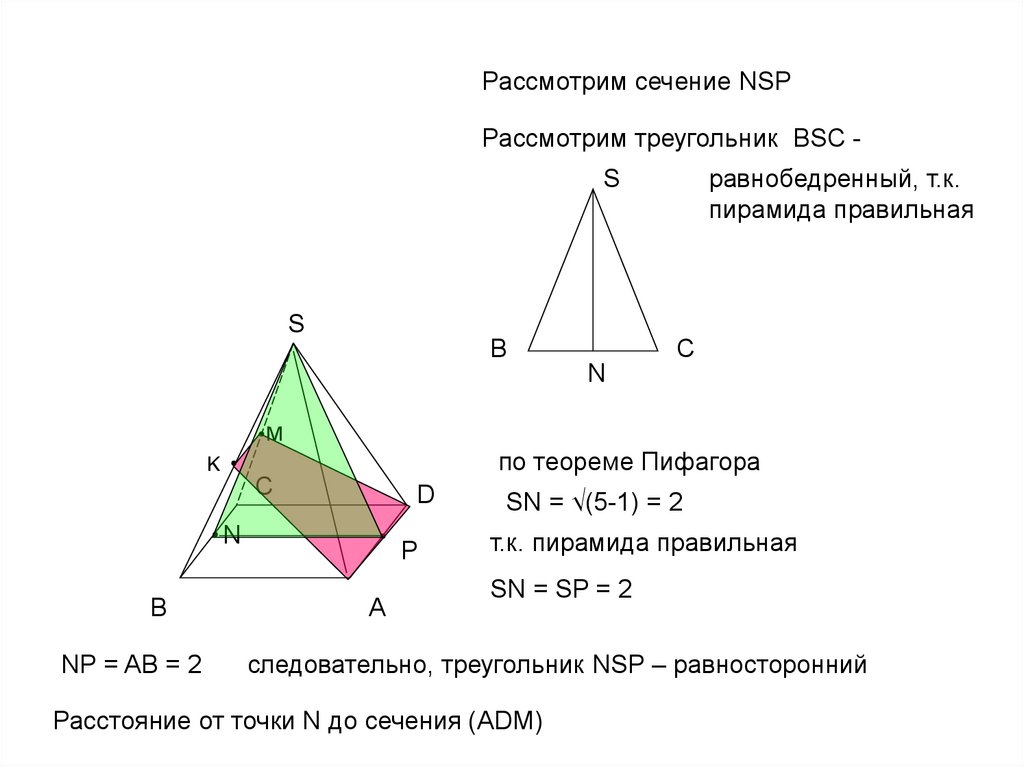
Рассмотрим сечение NSP
Рассмотрим треугольник BSC равнобедренный, т.к.
пирамида правильная
S
S
B
C
N
M
K
по теореме Пифагора
С
D
N
В
NP = AB = 2
P
А
SN = √(5-1) = 2
т.к. пирамида правильная
SN = SP = 2
следовательно, треугольник NSP – равносторонний
Расстояние от точки N до сечения (ADM)

5.

следовательно, треугольник NSP – равносторонний
NP = AB = 2
SN ∩ KM = O
ОР – медиана, биссектриса и ВЫСОТА, т.к. треугольник равносторонний
РМ перпендикулярна КМ, следовательно
Расстояние от точки N до сечения (ADM) - расстояние от точки N до КМ
S
O
K
О – середина SN
M
ON = 1/2SN = 1
С
D
N
В
P
А