Подготовка к ЕГЭ. Задачи по геометрии в вариантах ЕГЭ

1.

2.

3.

4.

Сегодня на уроке.
1) Целеполагание.
2) Геометрическая разминка.
3) Повторим планиметрию.
Решение задач из ЕГЭ(часть В).
4) Решение задач из ЕГЭ(часть С).
5) Домашнее задание.
6) Подведение итогов.

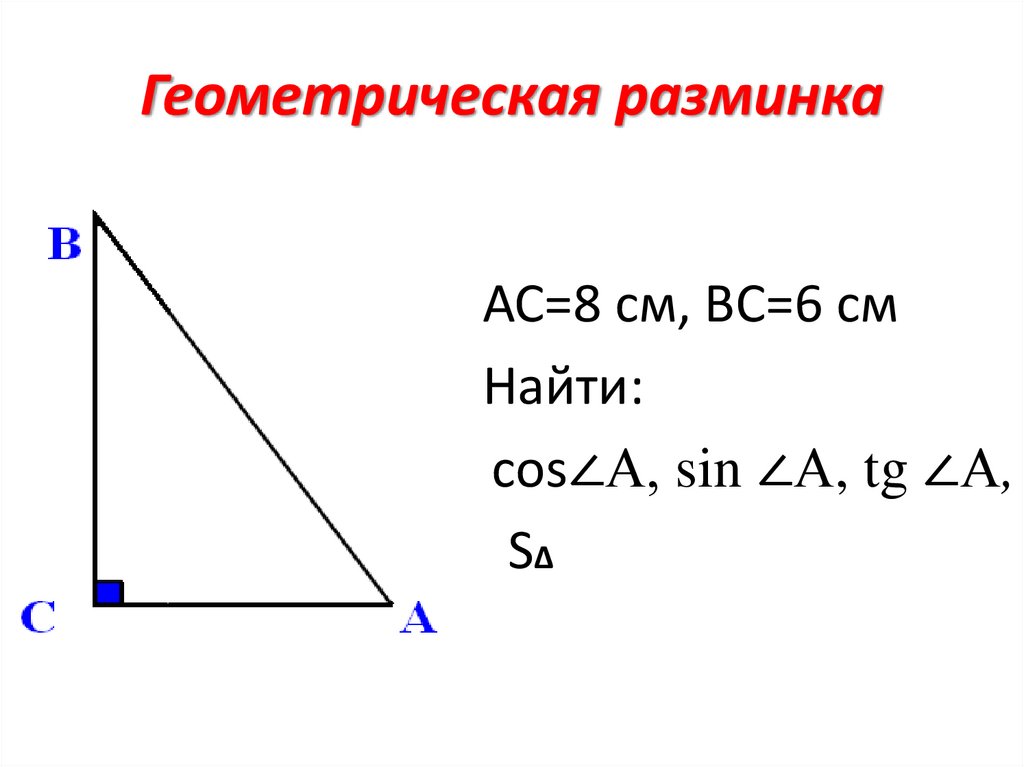
5. Геометрическая разминка

АС=8 см, ВС=6 см
Найти:
соs∠А, sin ∠А, tg ∠А,
S∆

6. Геометрическая разминка

АВ=ВС=17см,
АС=30см
Найти: ВН, S∆

7. Геометрическая разминка

8. Геометрическая разминка

Р
В
Д
С
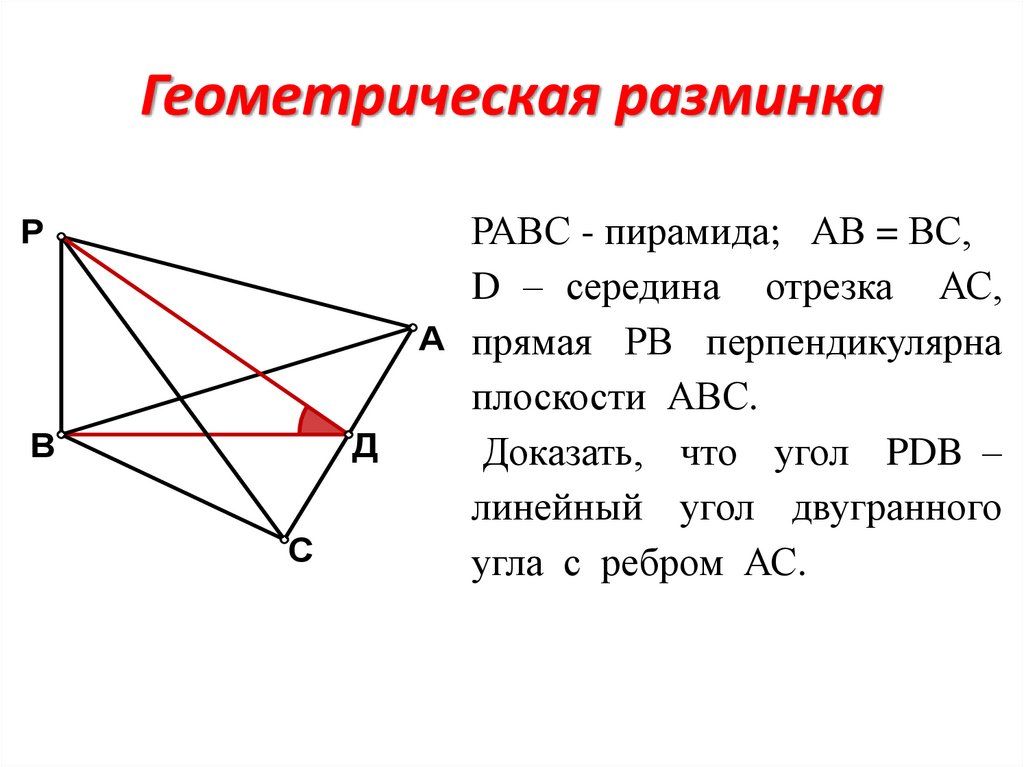
РАВС - пирамида; АВ = ВС,
D – середина отрезка АС,
А прямая РВ перпендикулярна
плоскости АВС.
Доказать, что угол PDB –
линейный угол двугранного
угла с ребром АС.

9. Ответ: 14

В4
Решение
1. tg A =
АС=
,
=
=
=
2. По теореме Пифагора
находим АВ
=
=
Ответ: 14
=14

10. Решение

В4
Решение
1. Проведем высоту ВH, АВН прямоугольный
cos A= .
Имеем АH = AВ cos A =
.
2. По теореме Пифагора
находим BH =
Ответ: 4
= 4.

11.

С2
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2 ,
а диагональ боковой грани равна
. Найдите угол между плоскостью
A1BC и плоскостью основания призмы.
Решение
H середина ребра BC.
ABC равносторонний, а
A1 BC – равнобедренный,
отрезки AH и A1H перпендикулярны BC .
∠A1HA – линейный угол двугранного угла с
гранями BCA и BCA1 .
Из A1 AB : AA1 =1.
Из AHB: AH = .
Из HAA1 найдем:
tg ∠ A1HA=
=
Искомый угол равен 30° .
Ответ: 30°

12.

В правильной треугольной пирамиде SABC с основанием ABC известны
ребра: AB 8 3 , SC 17. Найдите угол, образованный плоскостью
основания и прямой, проходящей через середины ребер AS и BC .
Решение
SО – высота, O ϵ АМ
KH ||SO, KH (АВС), KH АМ,
МН – проекция МК на (АВС)
∠KMH – угол между прямой МК и (АВС).
SOА КН – средняя линия, OH = HA
СМ=МВ= 4 3.
2
2
АМ = AB 2 MB 2
8 3 4 3 12
АН = 1∕3 АМ=4, МН =2∕3 АМ=8
АК = 1∕2 SА= 17∕2
КН =
Из
=
МКН tg ∠KMH =
= 7,5
KH
7,5 15
.
MH
8
16
KMH arctg
15
.
16

13. Домашнее задание

Сборник заданий В4: № 2347,2395
Сборник заданий С2:
тр. работа 2 – №4, тр.работа3 – №3

14.

Человек…родился быть
господином, царём природы, но
мудрость, с которой он должен
править… не дана ему от рождения:
она приобретается учением.
Н.И. Лобачевский