Решение задач

1. Задача 1 (угол между прямыми)

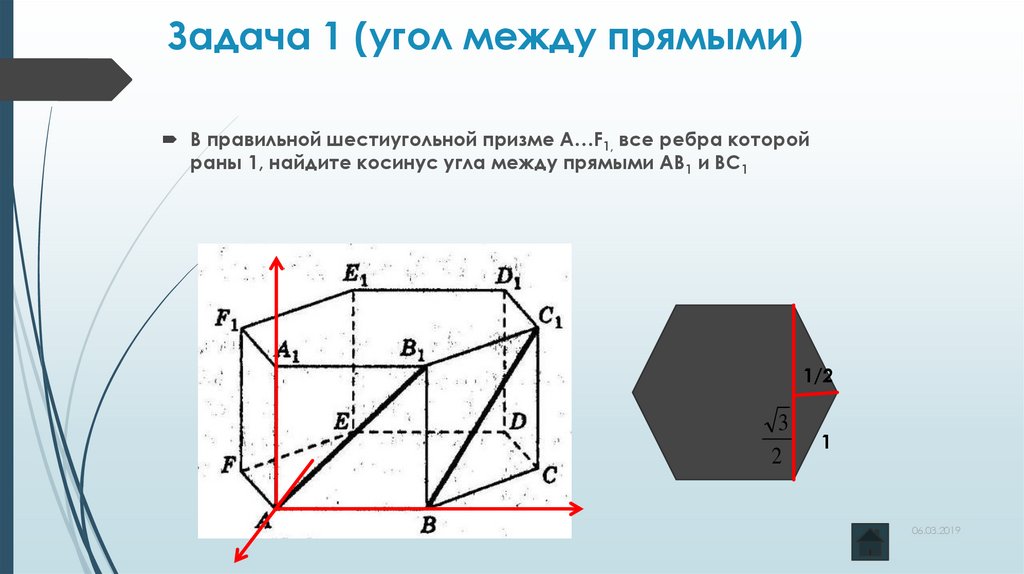
В правильной шестиугольной призме А…F1, все ребра которой
раны 1, найдите косинус угла между прямыми АВ1 и ВС1
1/2
3
2
1
06.03.2019

2. Решение задачи 1

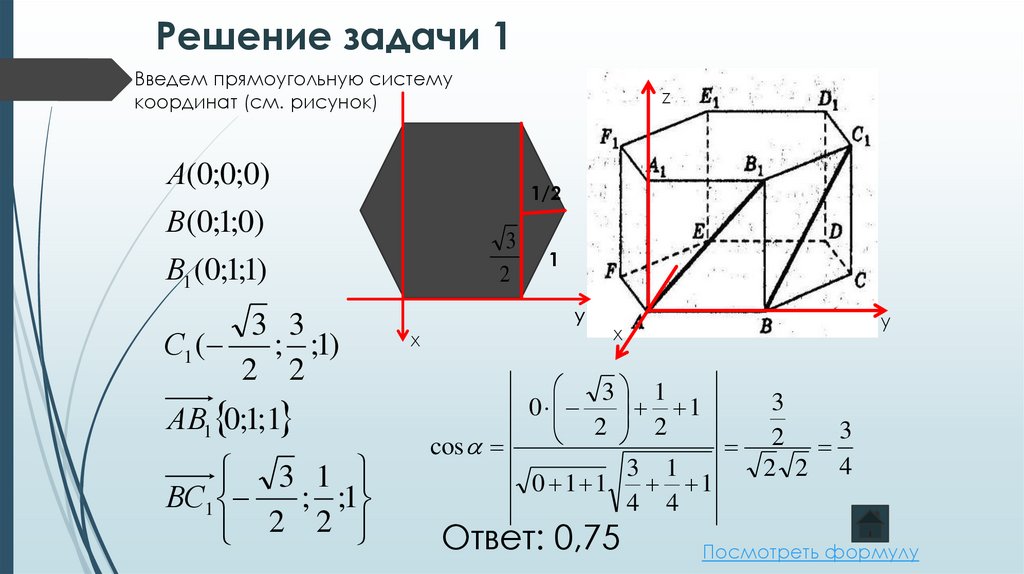
Введем прямоугольную систему
координат (см. рисунок)
z
А(0;0;0)
1/2
В(0;1;0)
3
2
В1 (0;1;1)
3 3
С1 (
; ;1)
2 2
АВ1 0;1;1
3 1
ВС1
; ;1
2 2
1
y
x
у
х
3 1
3
1
0
2 2
3
2
cos
3 1
2 2 4
0 1 1
1
4 4
Ответ: 0,75
Посмотреть формулу

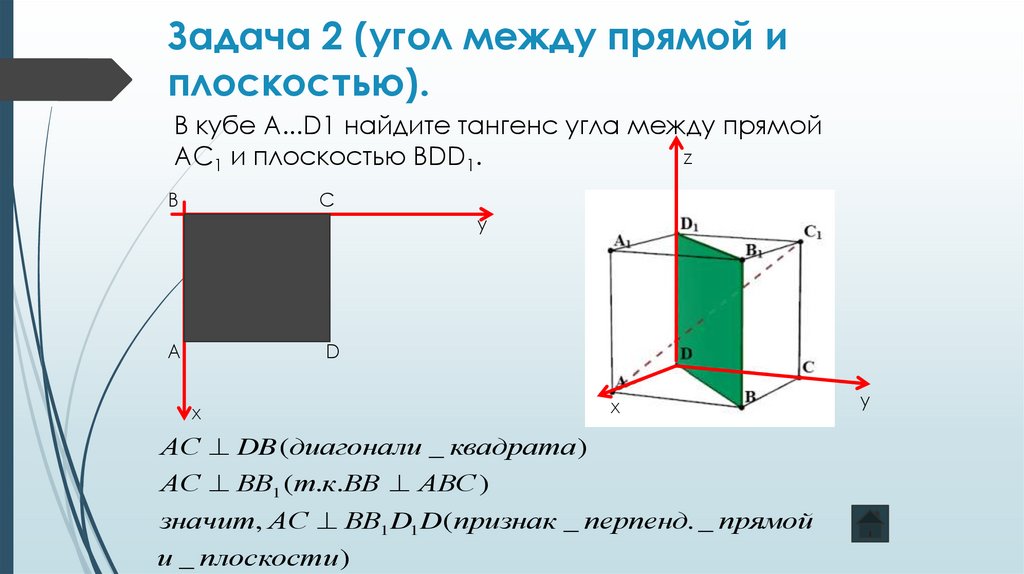
3. Задача 2 (угол между прямой и плоскостью).

В кубе A...D1 найдите тангенс угла между прямой
z
AC1 и плоскостью BDD1.
В
С
y
А
D
х
х
АС DB (диагонали _ квадрата )
АС ВВ1 ( т.к.ВВ АВС )
значит, АС ВВ1 D1 D ( признак _ перпенд. _ прямой
и _ плоскости )
у

4. Решение задачи 2

z
Решение задачи 2
Введем прямоугольную систему
координат (см. рисунок)
В
С
y
А
D
х
А(1;0;0)
С(0;1;0)
С1(0;1;1)
АС 1;1;0
у
х
Пусть α – искомый угол)
АС1 1;1;1
1 1 0
2
sin cos( АС ˆ; АС1 )
1 1 0 1 1 1
6
4
1
соs 1
6
3
tg 2
Посмотреть формулу
Ответ : 2

5. Задача 3.Угол между плоскостями

Задача 3.Угол между
В
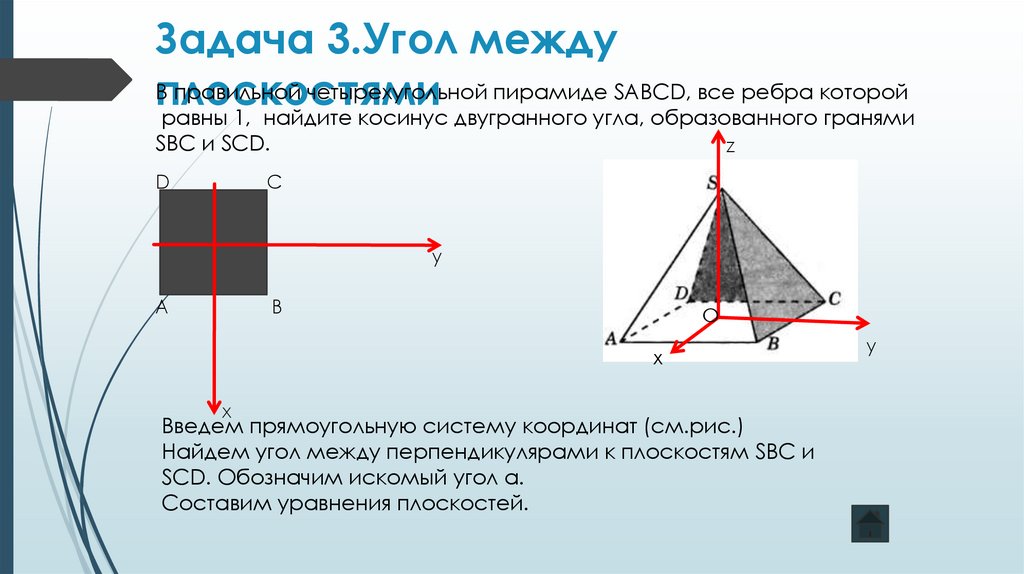
правильной четырехугольной пирамиде SABCD, все ребра которой
плоскостями
равны 1, найдите косинус двугранного угла, образованного гранями
SBC и SCD.
D
z
С
y
А
В
О
х
х
Введем прямоугольную систему координат (см.рис.)
Найдем угол между перпендикулярами к плоскостям SBC и
SCD. Обозначим искомый угол α.
Составим уравнения плоскостей.
у

6. Решение задачи 3

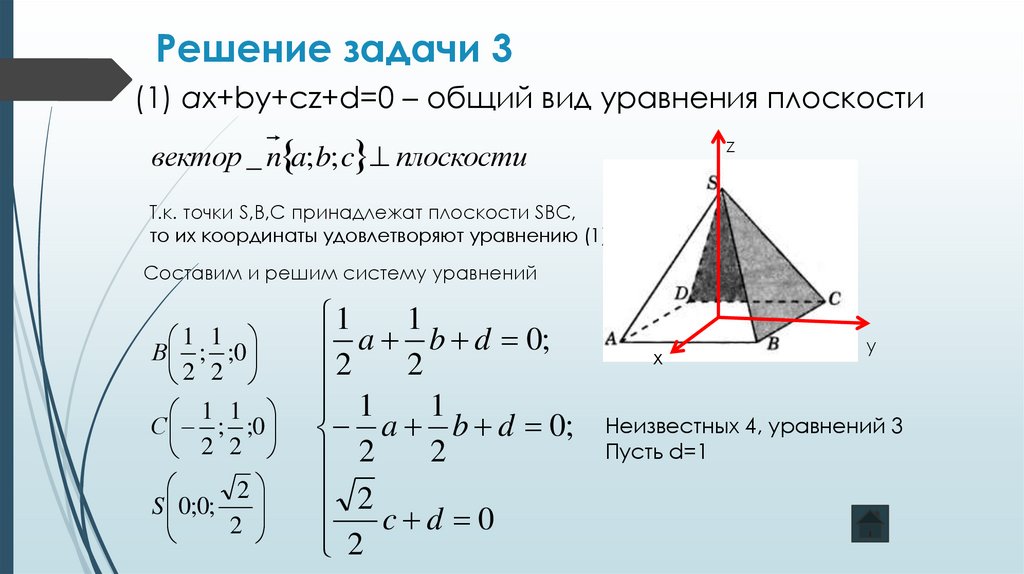
(1) aх+by+cz+d=0 – общий вид уравнения плоскости
вектор _ n a; b; c плоскости
z
Т.к. точки S,B,C принадлежат плоскости SBC,
то их координаты удовлетворяют уравнению (1)
Составим и решим систему уравнений
1 1
В ; ;0
2 2
1 1
С ; ;0
2 2
2
S 0;0;
2
1
1
2 a 2 b d 0;
1
1
a b d 0;
2
2
2
c d 0
2
х
у
Неизвестных 4, уравнений 3
Пусть d=1

7. Решение задачи 3(продолжение)

Аналогично найдем координаты
Вектора, перпендикулярного
плоскости SCD
a 0;
b 2;
c 2 ;
d 1.
2
S 0;0;
2
1 1
C ; ;0
2 2
1 1
D ; ;0
2 2
m 2;0; 2 SCD
n 0; 2; 2 SBC
cos
Ответ :
1
3
z
0 0 2
4 2 4 2
1
3
у
х
2
с d 0;
2
1
1
a b d 0;
2
2
1
1
2 a 2 b d 0.
a 2;
b 0;
c 2 ;
d 1.

8. Задача 4 (Расстояние от точки до прямой)

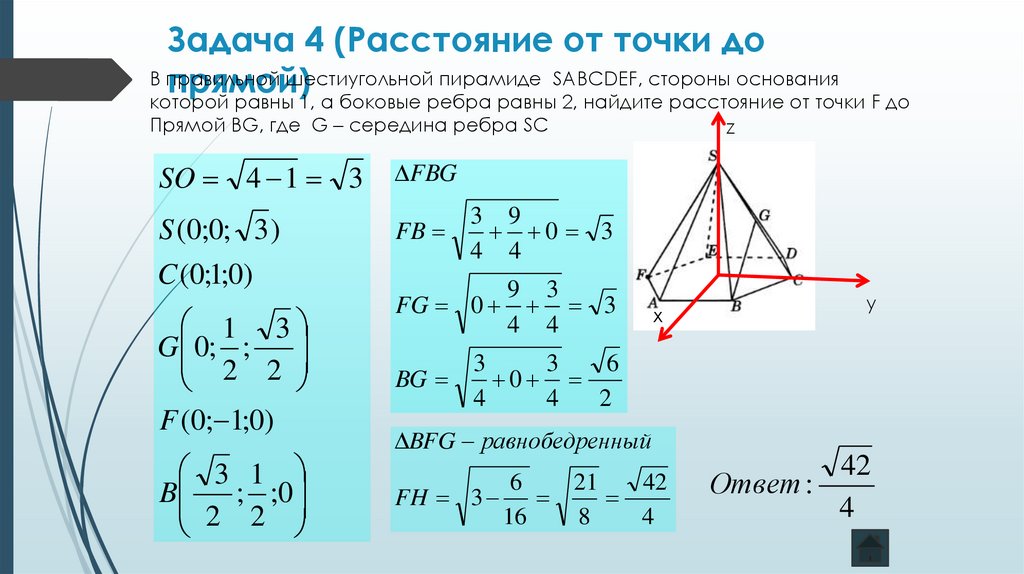
Задача 4 (Расстояние от точки до
В правильной
шестиугольной пирамиде SABCDEF, стороны основания
прямой)
которой равны 1, а боковые ребра равны 2, найдите расстояние от точки F до
Прямой BG, где G – середина ребра SC
SO 4 1 3
S (0;0; 3 )
C (0;1;0)
1 3
G 0; ;
2
2
F (0; 1;0)
3 1
B
; ;0
2 2
z
FBG
FB
3 9
0 3
4 4
9 3
FG 0 3
4 4
BG
х
у
3
3
6
0
4
4
2
BFG равнобедренный
6
21
42
FH 3
16
8
4
42
Ответ :
4

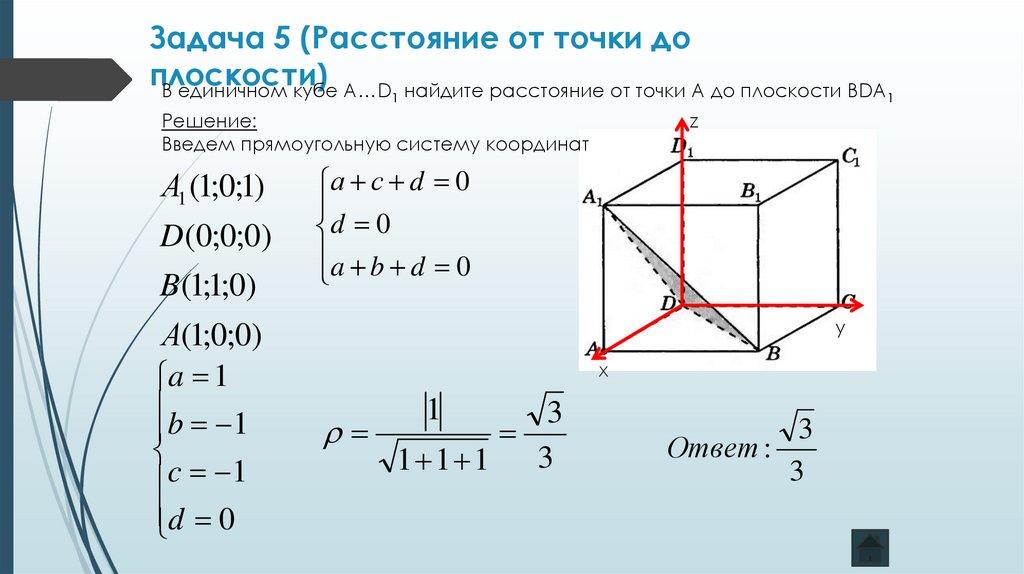
9. Задача 5 (Расстояние от точки до плоскости)

В единичном кубе А…D найдите расстояние от точки А до плоскости ВDA
1
Решение:
Введем прямоугольную систему координат
А1 (1;0;1)
D (0;0;0)
B (1;1;0)
А(1;0;0)
a 1
b 1
c 1
d 0
z
а с d 0
d 0
a b d 0
у
х
1
3
3
1 1 1
3
Ответ :
3
1

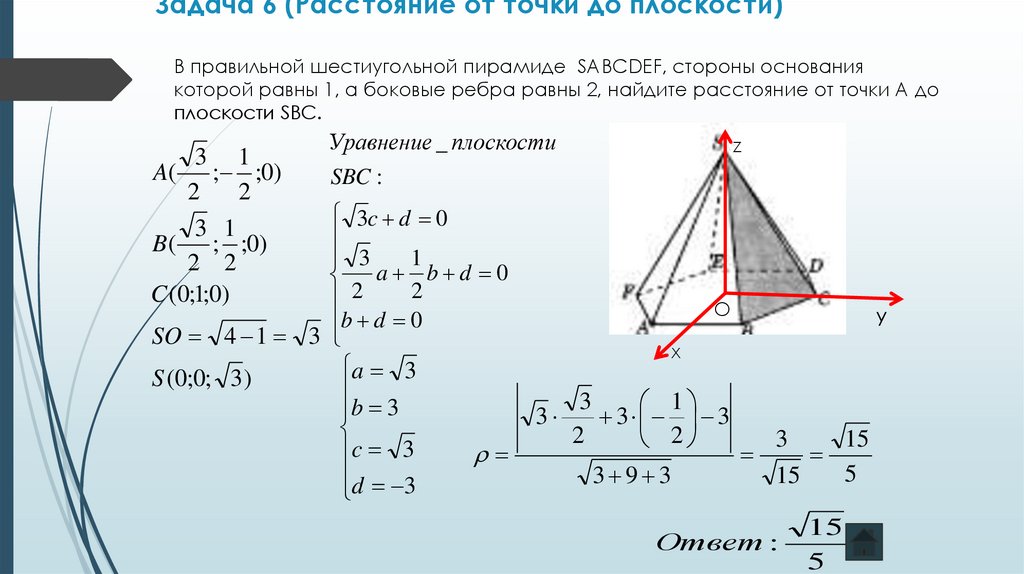
10. Задача 6 (Расстояние от точки до плоскости)

В правильной шестиугольной пирамиде SABCDEF, стороны основания
которой равны 1, а боковые ребра равны 2, найдите расстояние от точки А до
плоскости SBC.
3 1
A( ; ;0)
2
2
3 1
B ( ; ;0)
2 2
C (0;1;0)
Уравнение _ плоскости
z
SBC :
3c d 0
1
3
a
b d 0
2
2
b d 0
SO 4 1 3
S (0;0; 3 )
a 3
b 3
c 3
d 3
O
у
х
3
1
3
3 3
2
2
3 9 3
3
15
5
15
Ответ :
15
5