Похожие презентации:
Прямые и плоскости в пространстве
1.
Часть 1Презентацию подготовила учитель математики
МБОУ СОШ №4 г.Покачи ХМАО-Югра
Литвинченко Л.В.
2.
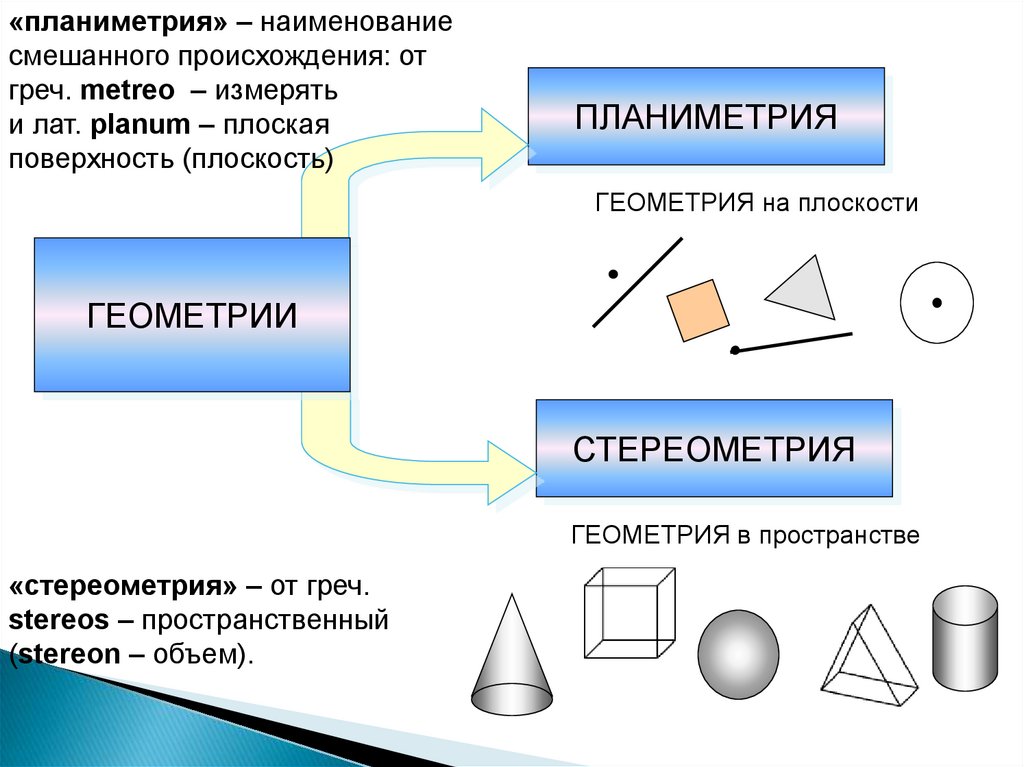
«планиметрия» – наименованиесмешанного происхождения: от
греч. metreo – измерять
и лат. planum – плоская
поверхность (плоскость)
ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ на плоскости
ГЕОМЕТРИИ
СТЕРЕОМЕТРИЯ
ГЕОМЕТРИЯ в пространстве
«стереометрия» – от греч.
stereos – пространственный
(stereon – объем).
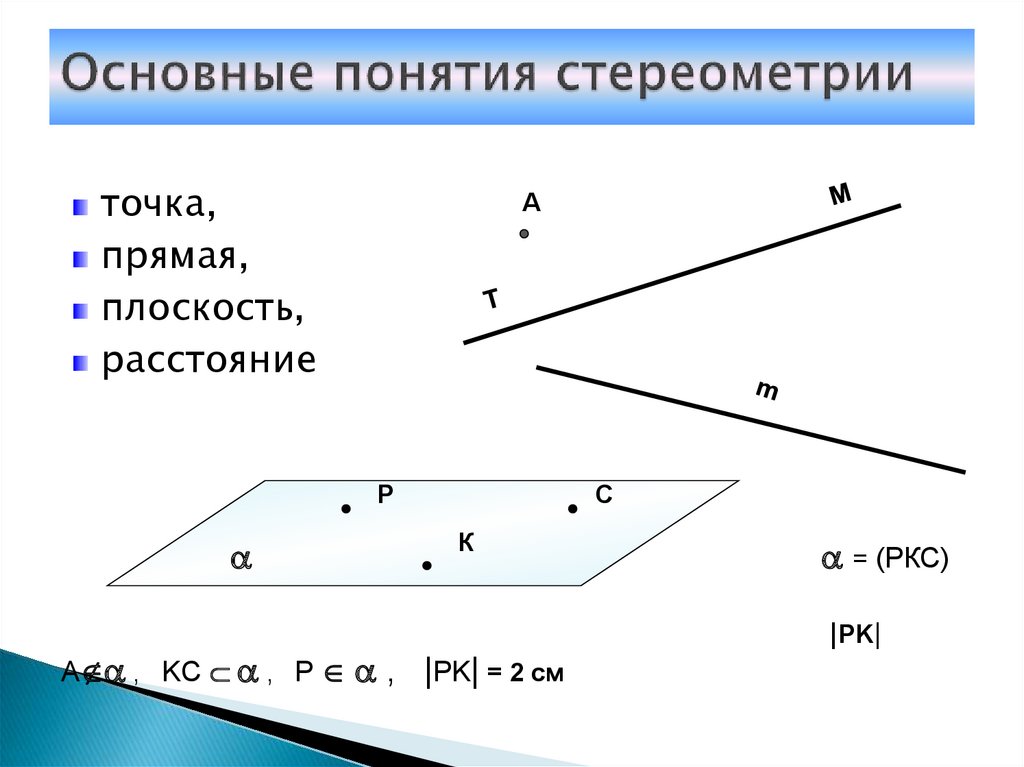
3. Основные понятия стереометрии
точка,прямая,
плоскость,
расстояние
А
Р
С
К
A , KC , P , |PK| = 2 см
= (РКС)
|PK|
4. ВСПОМНИМ ПЛАНИМЕТРИЮ
Каково может быть взаимное расположениедвух прямых на плоскости?
Какие прямые в планиметрии называются
параллельными?
5. ВСПОМНИМ ПЛАНИМЕТРИЮ
Аксиома параллельных прямых - ?Через точку, не лежащую на данной прямой,
проходит прямая, параллельная данной и притом
только одна
6. ВСПОМНИМ ПЛАНИМЕТРИЮ
Следствия аксиомы параллельных прямых ?Если прямая пересекает одну из параллельных
прямых, то она пересекает и другую.
Если две прямые параллельны третьей
прямой, то они параллельны.
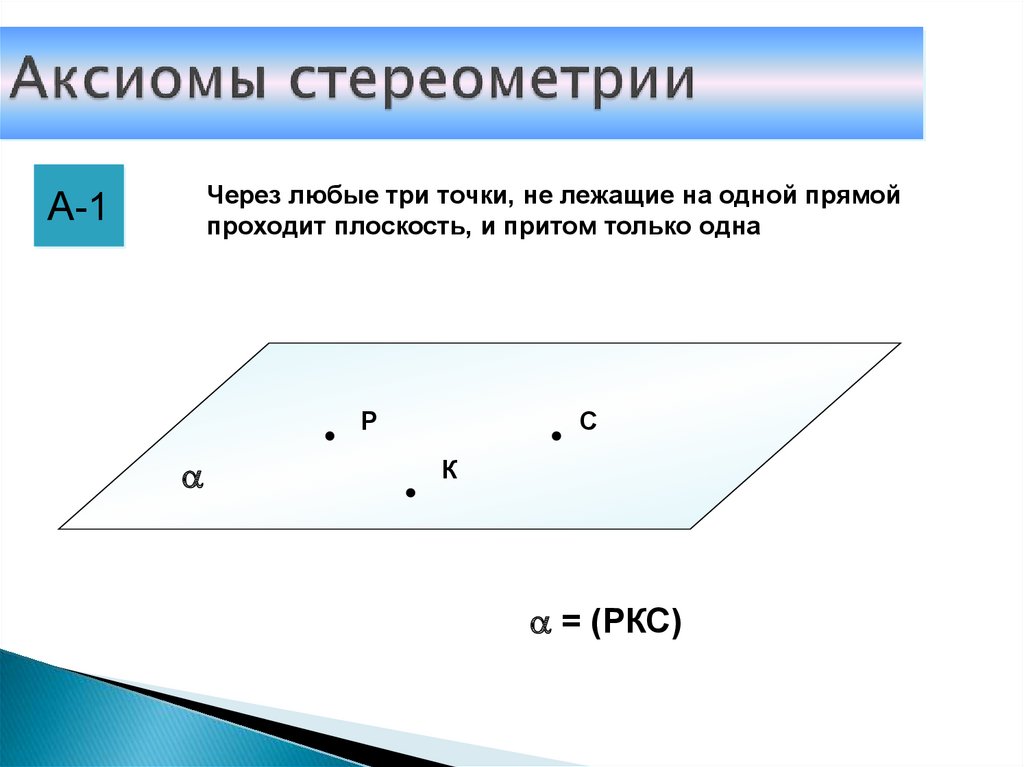
7. Аксиомы стереометрии
Через любые три точки, не лежащие на одной прямойпроходит плоскость, и притом только одна
А-1
Р
С
К
= (РКС)
8. Аксиомы стереометрии
А-2Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
Если
М, C
М, C m,
то
m
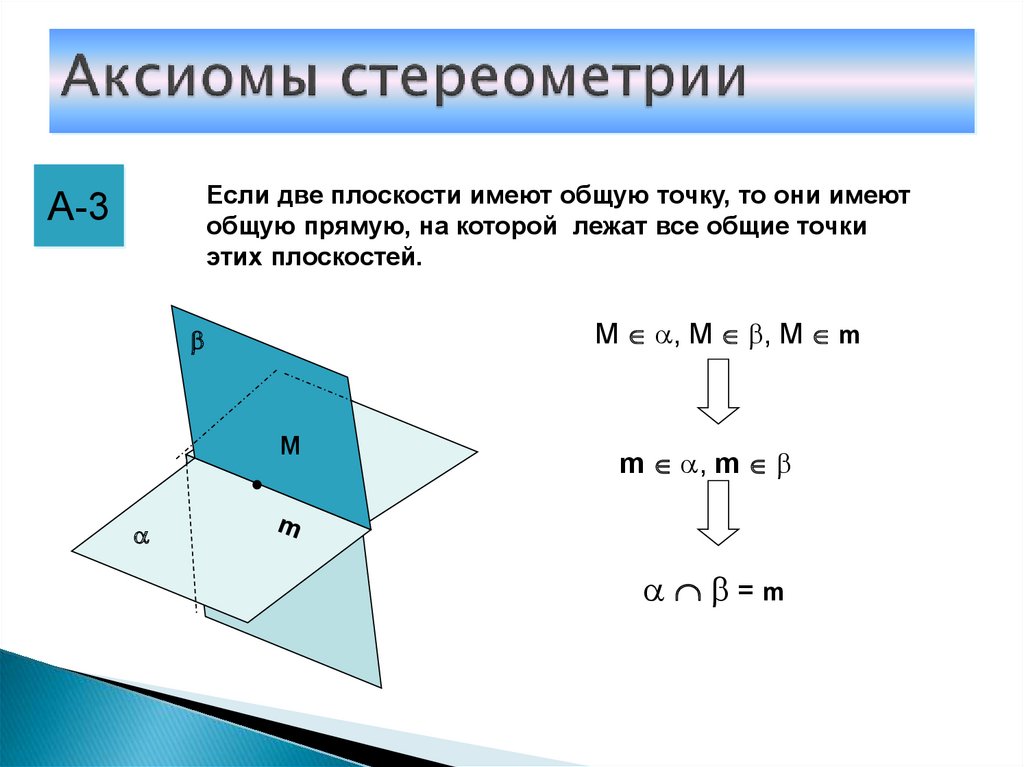
9. Аксиомы стереометрии
Если две плоскости имеют общую точку, то они имеютобщую прямую, на которой лежат все общие точки
этих плоскостей.
А-3
М , М , М m
М
m , m
=m
10. СЛЕДСТВИЯ ИЗ АКСИОМ
Через любую прямую и не принадлежащую ей точкуможно провести плоскость, и притом только одну.
Т-1
Дано: М m
В
А
м
Доказательство
Пусть точки A, B m.
Так как М m, то точки А, В и M не принадлежат одной прямой.
По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM),
Обозначим её . Прямая m имеет с ней две общие точки — точки A и B, следовательно,
по аксиоме А-2 эта прямая лежит в плоскости ..
Таким образом, плоскость проходит через прямую m и точку M и является искомой.
Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует.
Предположим, что есть другая плоскость — , проходящая через прямую m и точку M.
Тогда плоскости и проходят через точки А, В и M, не принадлежащие одной прямой, а
значит, совпадают. Следовательно, плоскость единственна.
Теорема доказана
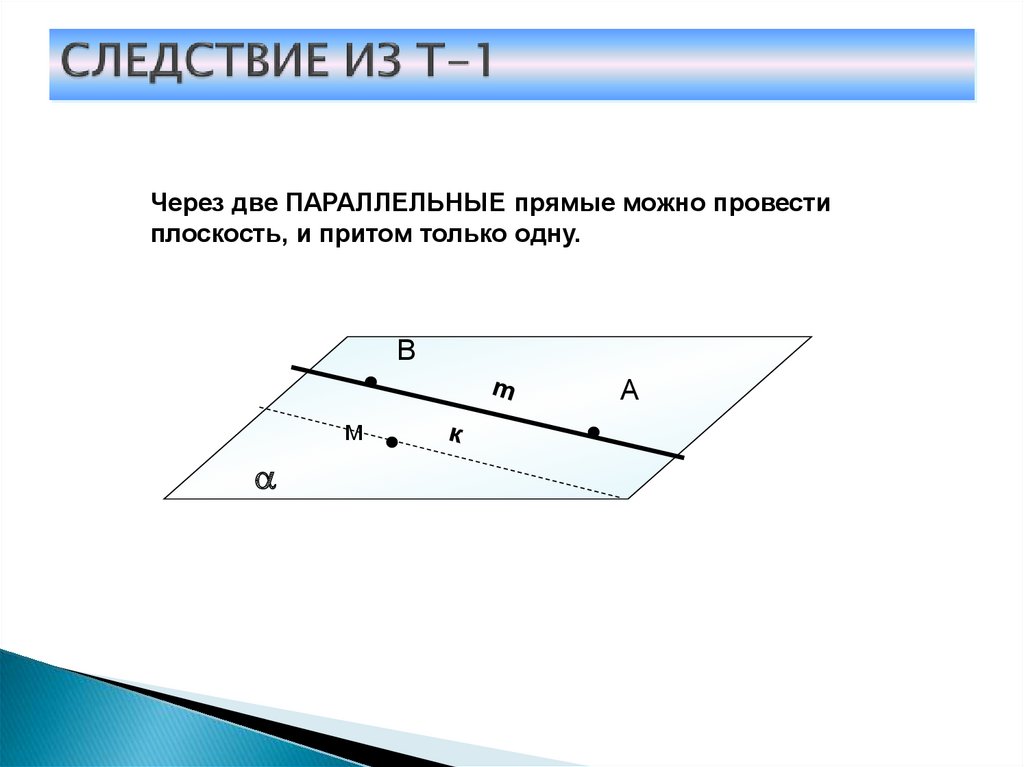
11. СЛЕДСТВИЕ ИЗ Т-1
Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провестиплоскость, и притом только одну.
В
А
м
12. СЛЕДСТВИЯ ИЗ АКСИОМ
Через любые две пересекающиеся прямые можнопровести плоскость, и притом только одну.
Т-2
n
м
N
Дано: m n = M
Доказательство
Отметим на прямой m произвольную точку N,
отличную от М.
Рассмотрим плоскость =(n, N). Так как M и N , то по А-2 m . Значит
обе прямые m, n лежат в плоскости и следовательно , является искомой
Докажем единственность плоскости . Допустим, что есть другая, отличная от
плоскости и проходящая через прямые m и n, плоскость .
Так как плоскость проходит через прямую n и не принадлежащую ей точку N, то по
T-1 она совпадает с плоскостью . Единственность плоскости доказана.
Теорема доказана
13. ВЫВОД
Как в пространстве можно однозначно задать плоскость?По
По
По
По
трем точкам, не лежащим на одной прямой
прямой и точке, не лежащей на этой прямой
двум пересекающимся прямым
двум параллельным прямым
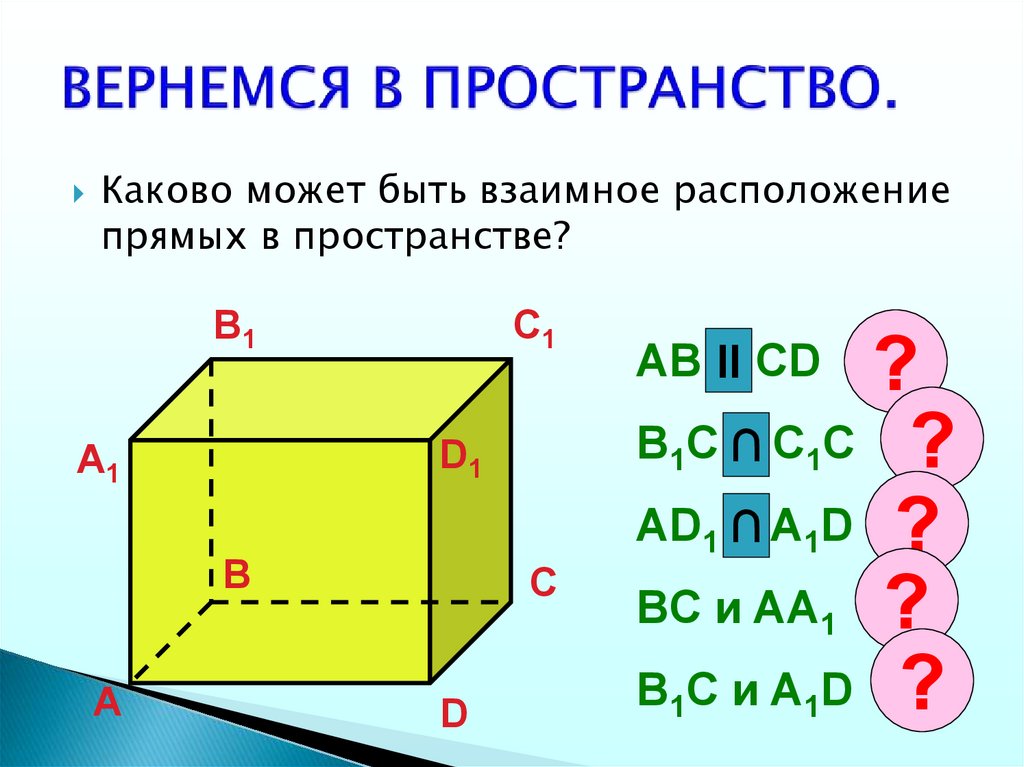
14. ВЕРНЕМСЯ В ПРОСТРАНСТВО.
Каково может быть взаимное расположениепрямых в пространстве?
B1
А1
C1
D1
?
B C∩
иC C ?
AD ∩
иA D ?
BC и AA ?
B CиA D ?
AB и
II CD
1
1
1
B
C
1
1
А
D
1
1
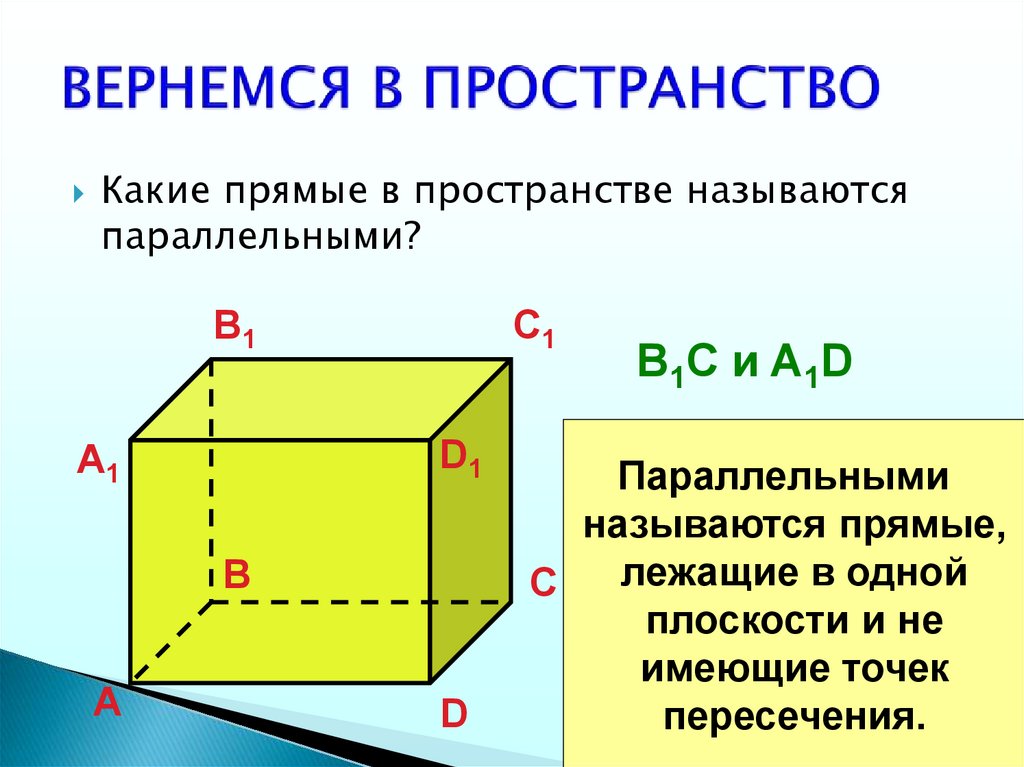
15. ВЕРНЕМСЯ В ПРОСТРАНСТВО
Какие прямые в пространстве называютсяпараллельными?
B1
А1
C1
D1
B
А
D
B1C и A1D
Параллельными
называются прямые,
лежащие в одной
C
плоскости и не
имеющие точек
пересечения.
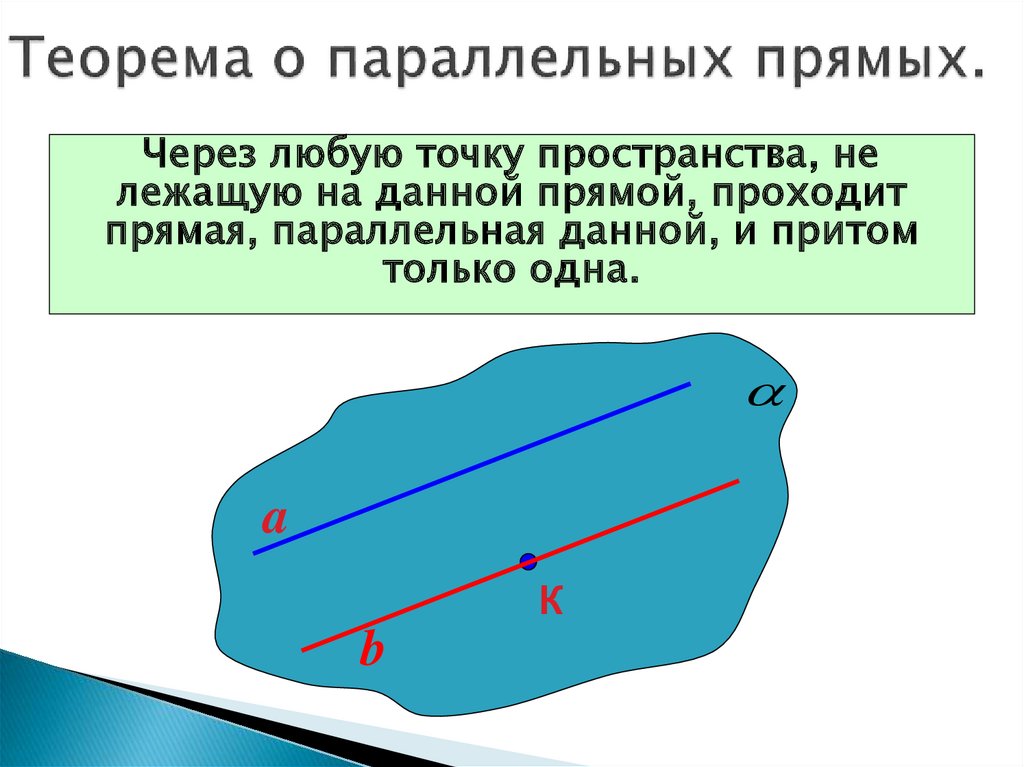
16. Теорема о параллельных прямых.
Через любую точку пространства, нележащую на данной прямой, проходит
прямая, параллельная данной, и притом
только одна.
a
К
b
17. …они лежат на параллельных прямых
Параллельные отрезки,параллельные лучи
в пространстве.
Отрезки в пространстве называются
параллельными, если …
Лучи в пространстве называются
параллельными, если …
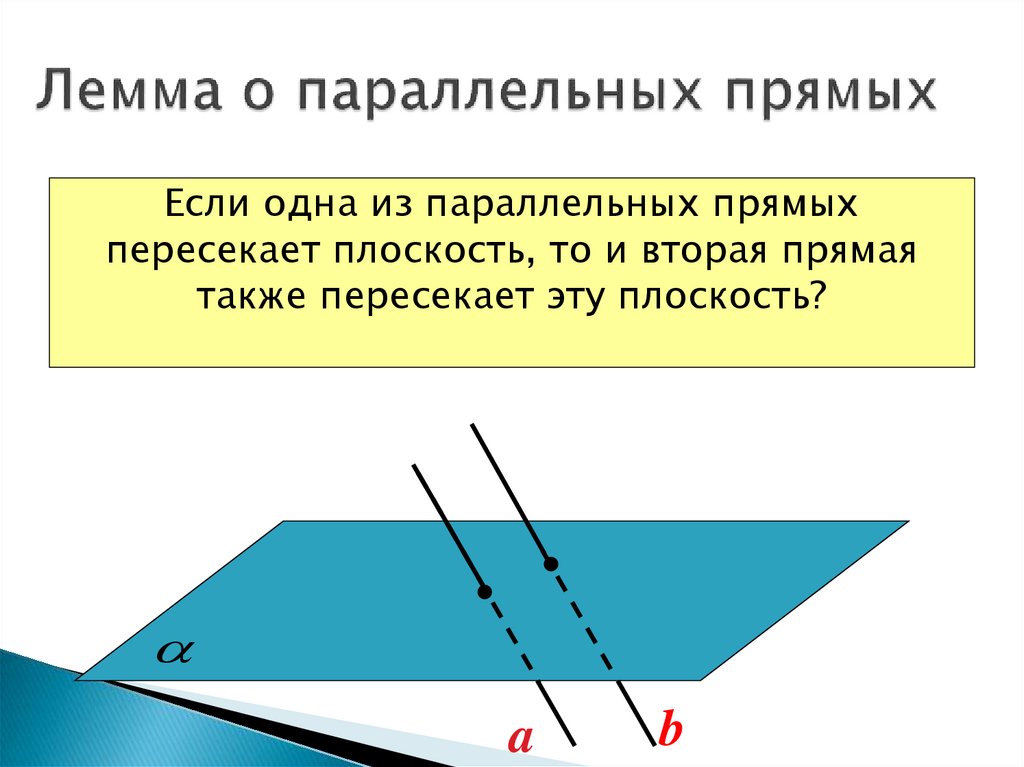
18. Лемма о параллельных прямых
Если одна из параллельных прямыхпересекает плоскость, то и вторая прямая
также пересекает эту плоскость?
a
b
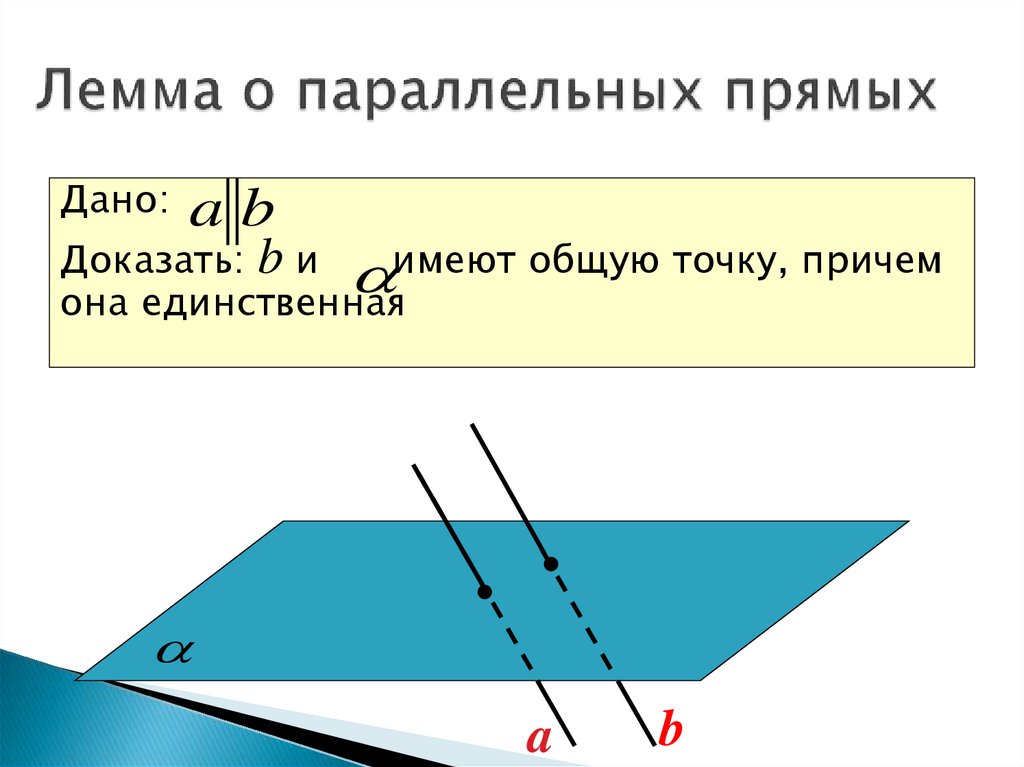
19. Лемма о параллельных прямых
Дано:ab
Доказать: b и имеют общую точку, причем
она единственная
a
b
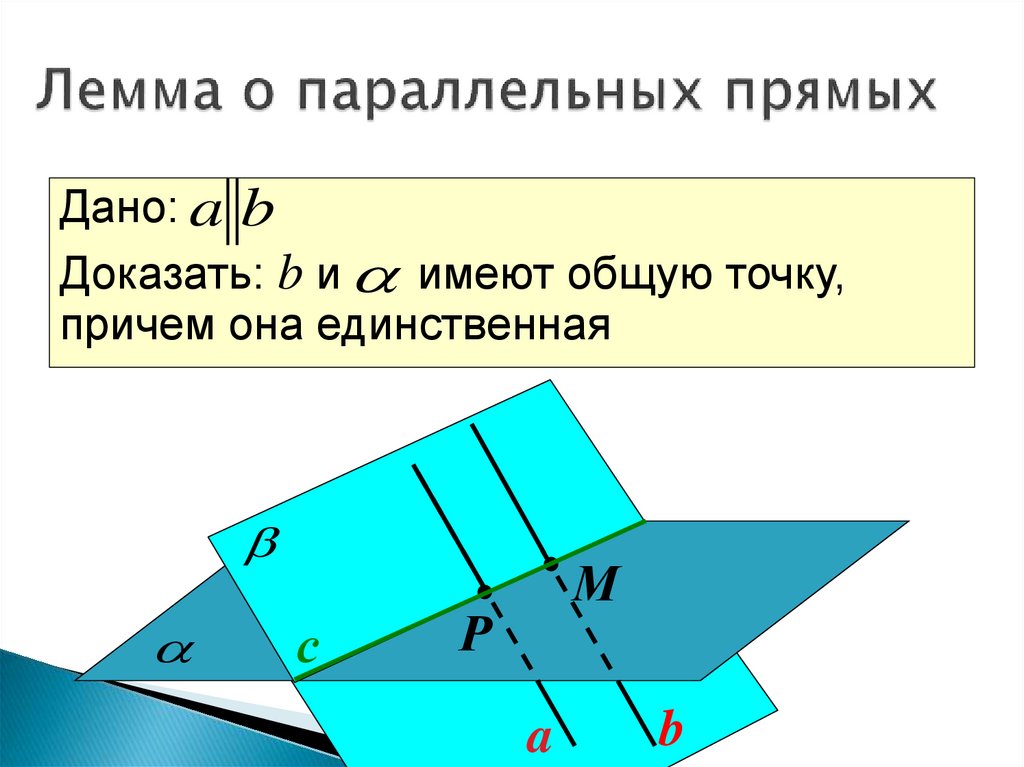
20. Лемма о параллельных прямых
Дано: a bДоказать: b и имеют общую точку,
причем она единственная
с
М
Р
a
b
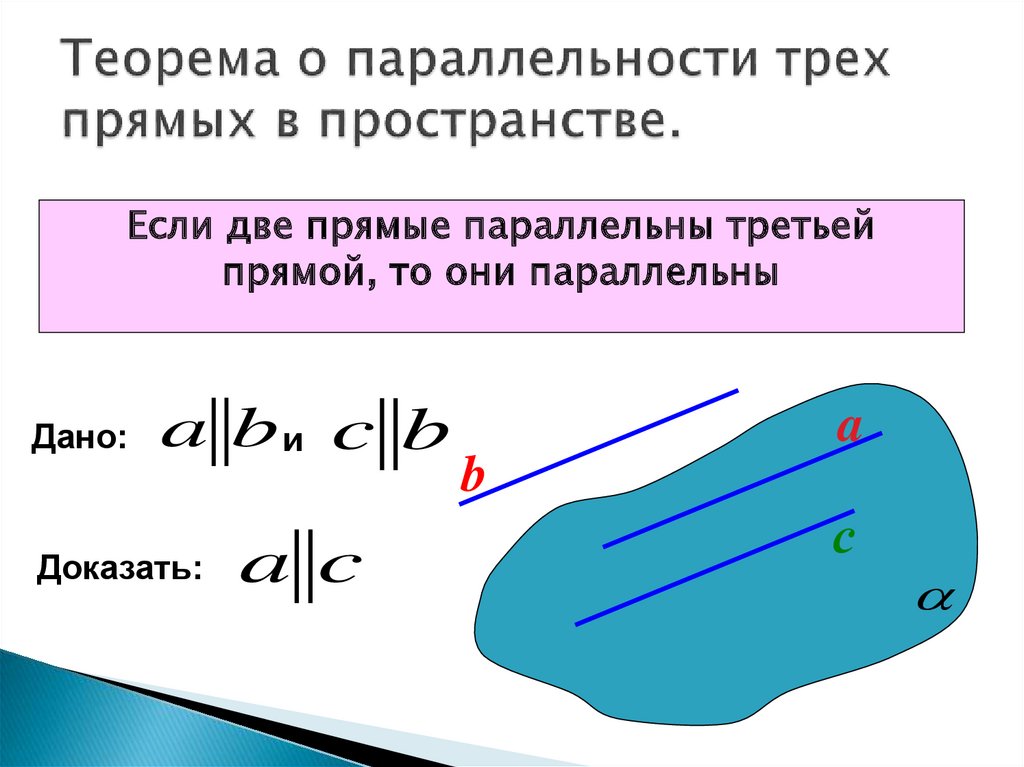
21. Теорема о параллельности трех прямых в пространстве.
Если две прямые параллельны третьейпрямой, то они параллельны
Дано:
a bи c b
Доказать:
a c
a
b
с
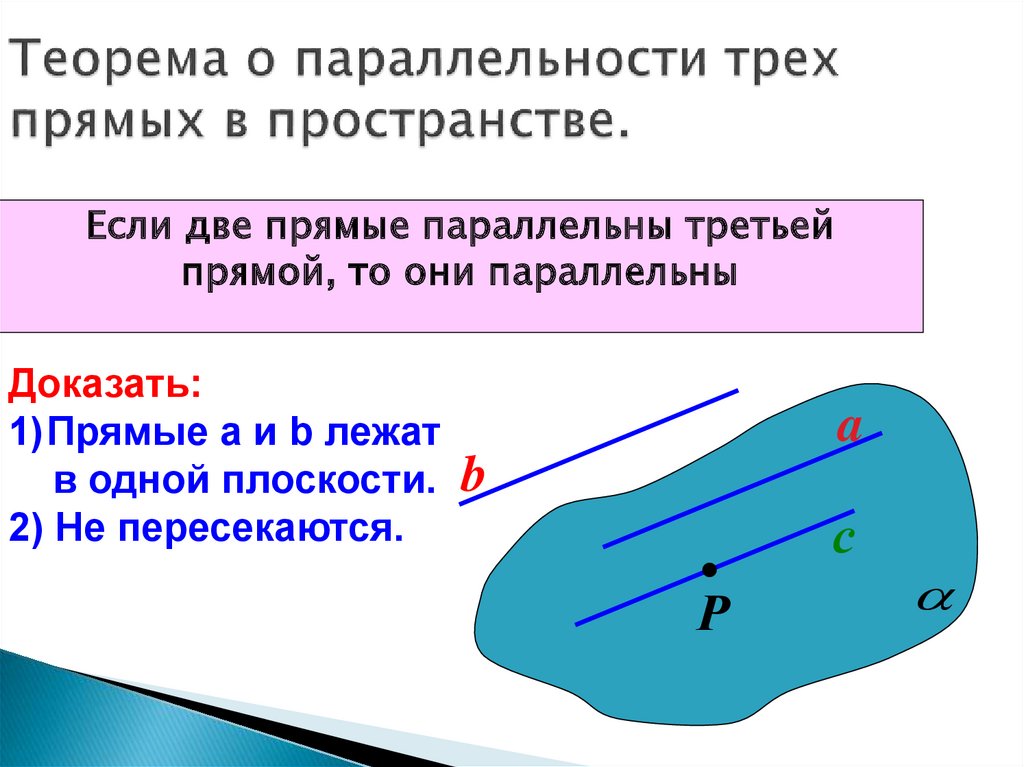
22. Теорема о параллельности трех прямых в пространстве.
Если две прямые параллельны третьейпрямой, то они параллельны
Доказать:
1)Прямые а и b лежат
в одной плоскости.
2) Не пересекаются.
a
b
с
Р
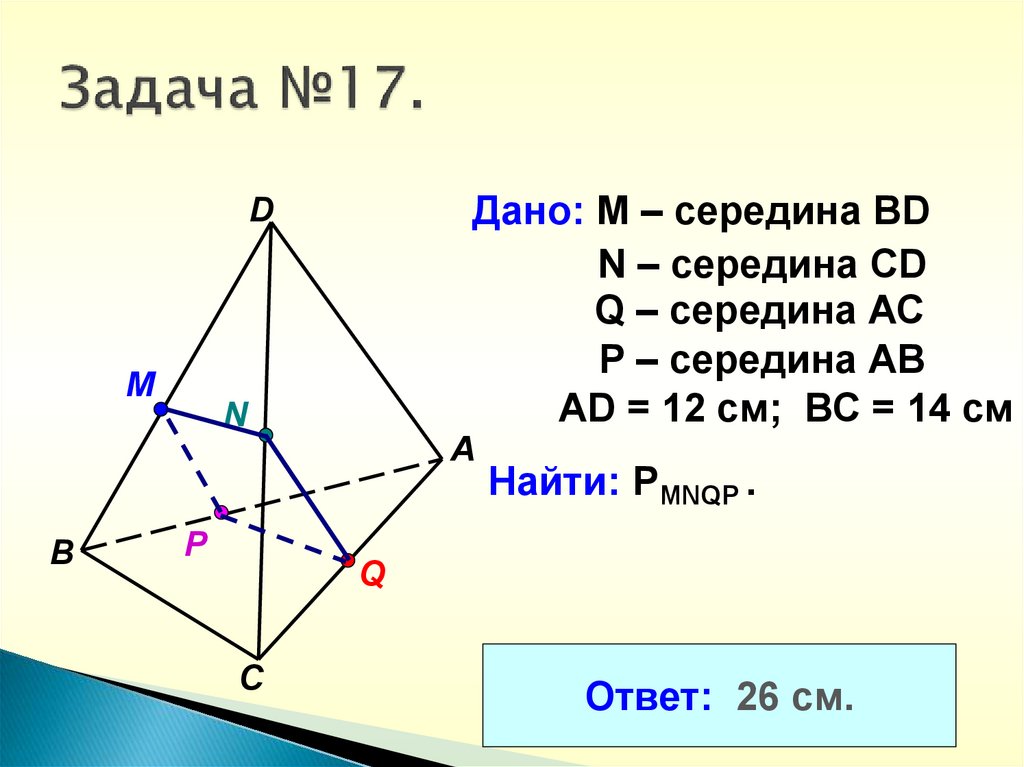
23. Задача №17.
Дано: М – середина BDN – середина CD
Q – середина АС
P – середина АВ
АD = 12 см; ВС = 14 см
D
M
N
A
B
Р
Найти: PMNQP .
Q
C
Ответ: 26 см.










 Математика
Математика








