Похожие презентации:
Решение задач на применение признаков равенства треугольников
1.
Тема урока:«Решение задач на применение
признаков равенства
треугольников».
Цель урока:
-повторение признаков равенства треугольников;
-формирование навыков применения признаков
равенства треугольников при решении задач.
2.
Вдохновение нужно в геометриине меньше, чем в поэзии.
А. С. Пушкин.
3.
ОТВЕТИМ НА ВОПРОСЫ ТЕСТА4.
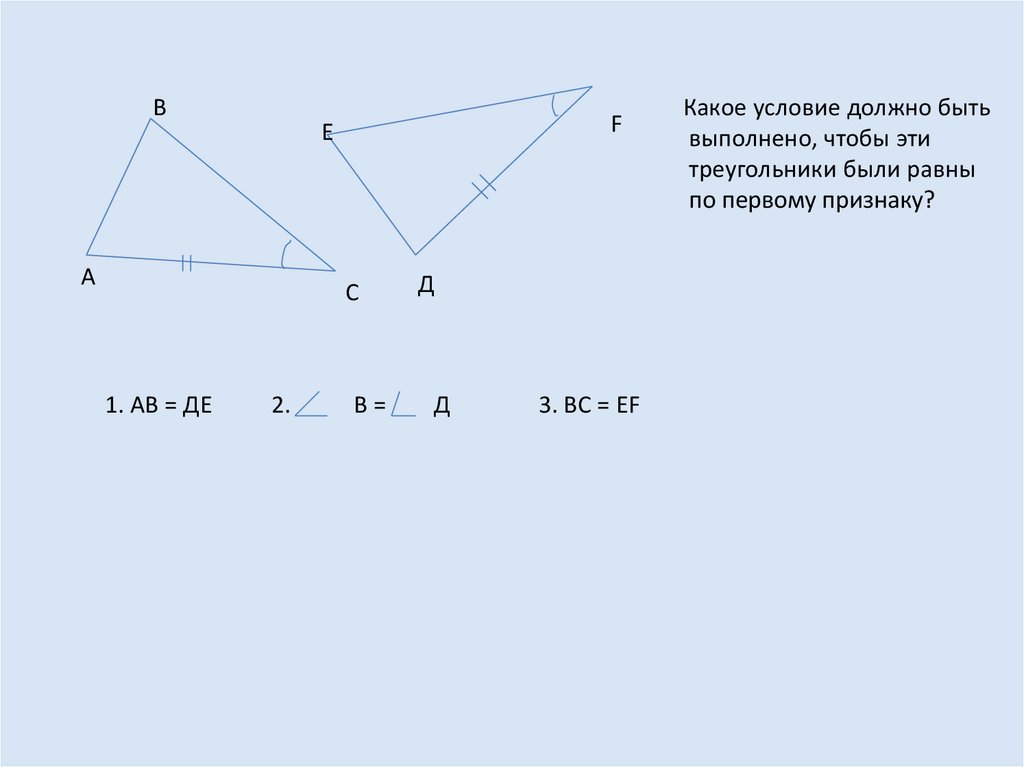
ВF
Е
А
С
1. АВ = ДЕ
2.
В=
Д
Д
3. ВС = ЕF
Какое условие должно быть
выполнено, чтобы эти
треугольники были равны
по первому признаку?
5.
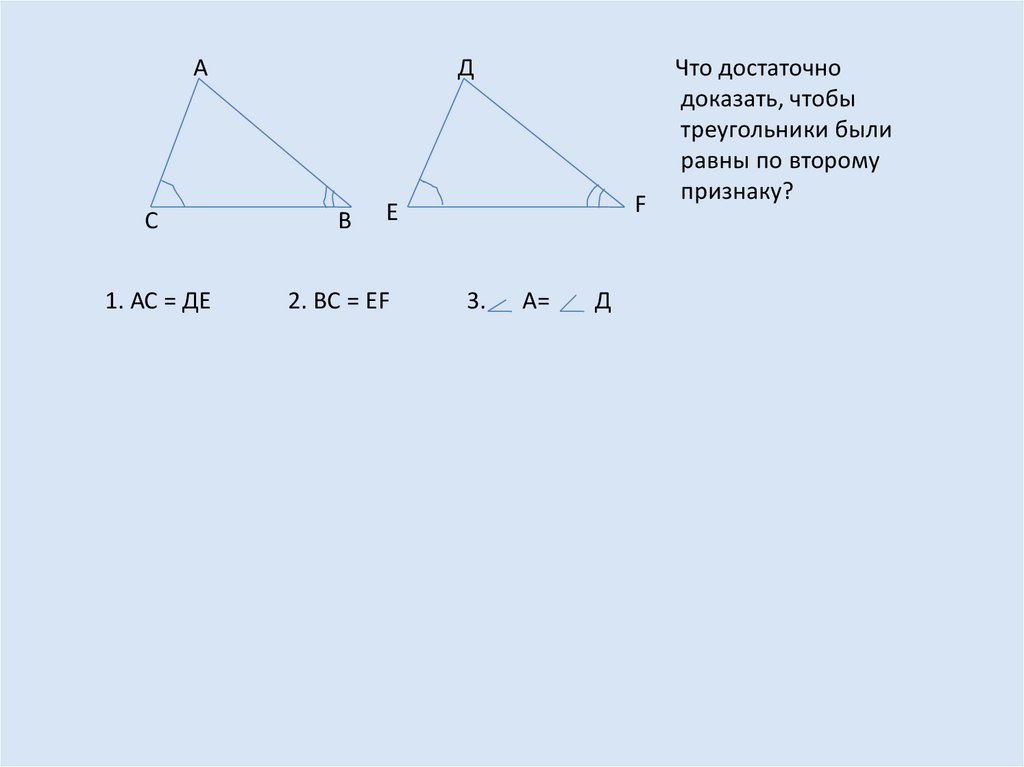
АД
F
Е
С
В
1. АС = ДЕ
2. ВС = ЕF
3.
А=
Д
Что достаточно
доказать, чтобы
треугольники были
равны по второму
признаку?
6.
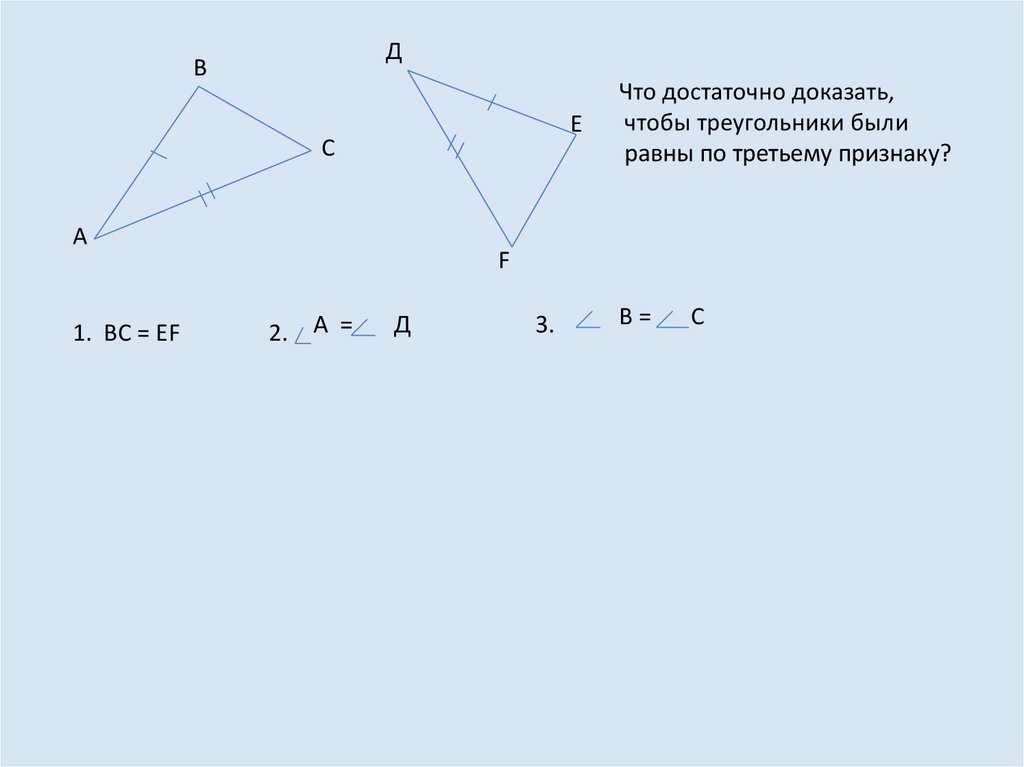
ДВ
Е
С
А
1. ВС = ЕF
Что достаточно доказать,
чтобы треугольники были
равны по третьему признаку?
F
2. А =
Д
3.
В=
С
7.
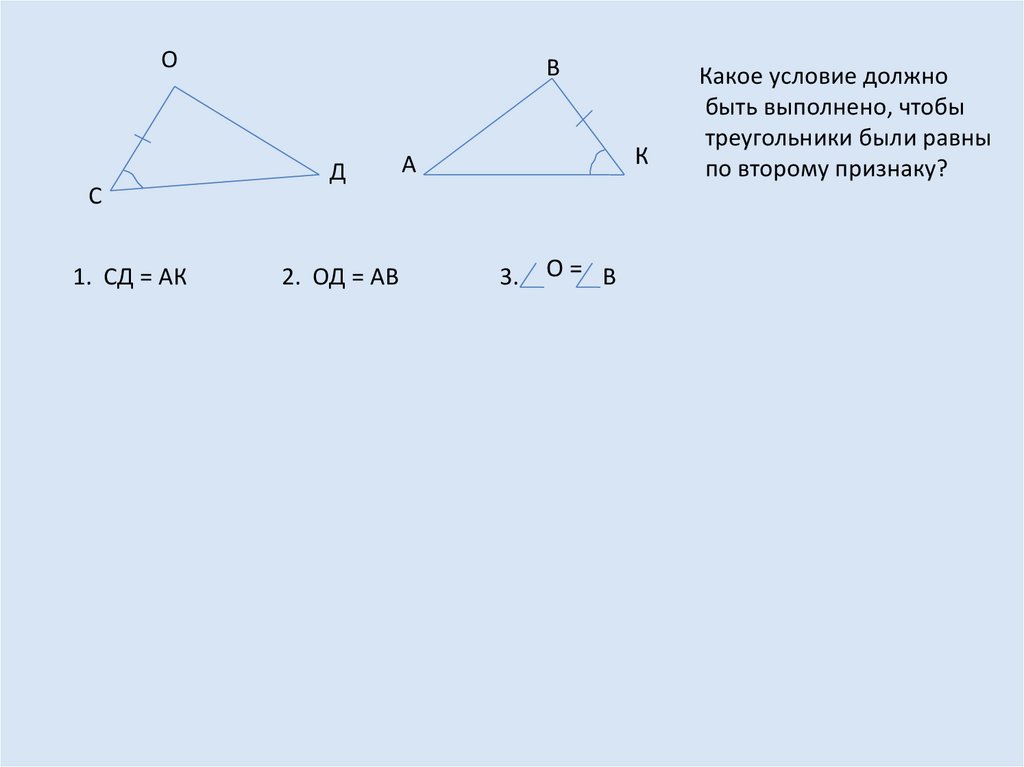
ОС
1. СД = АК
В
Д
2. ОД = АВ
К
А
3.
О= В
Какое условие должно
быть выполнено, чтобы
треугольники были равны
по второму признаку?
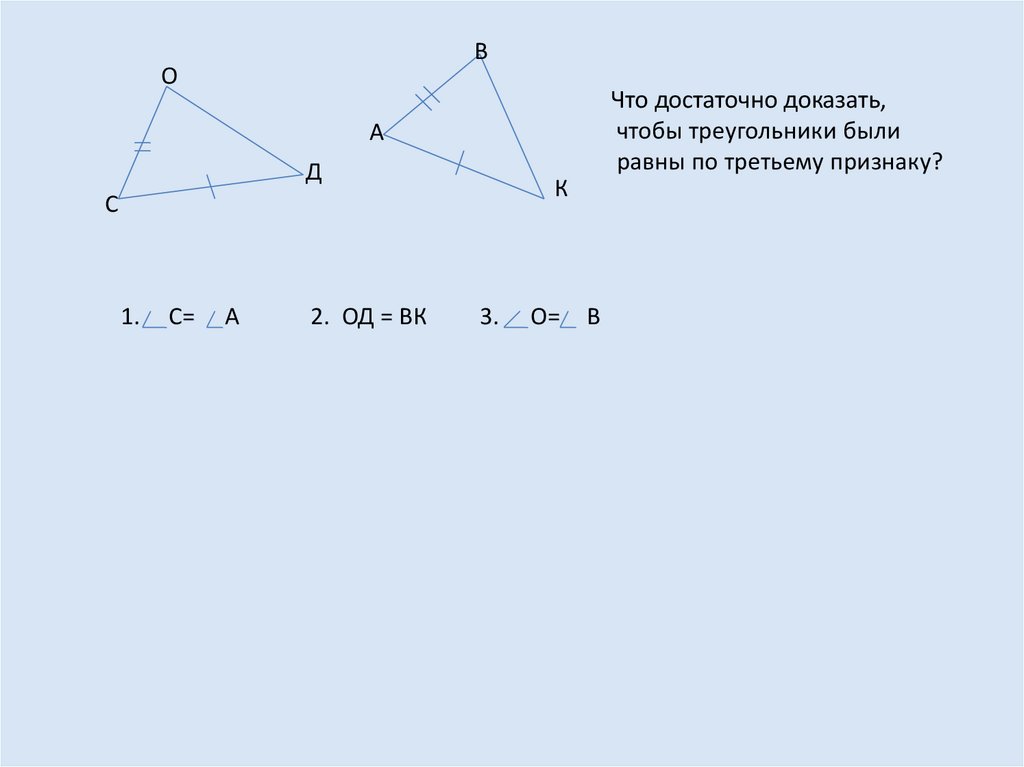
8.
ВО
Что достаточно доказать,
чтобы треугольники были
равны по третьему признаку?
А
Д
К
С
1.
С=
А
2. ОД = ВК
3.
О=
В
9.
ОА
Д
С
В
К
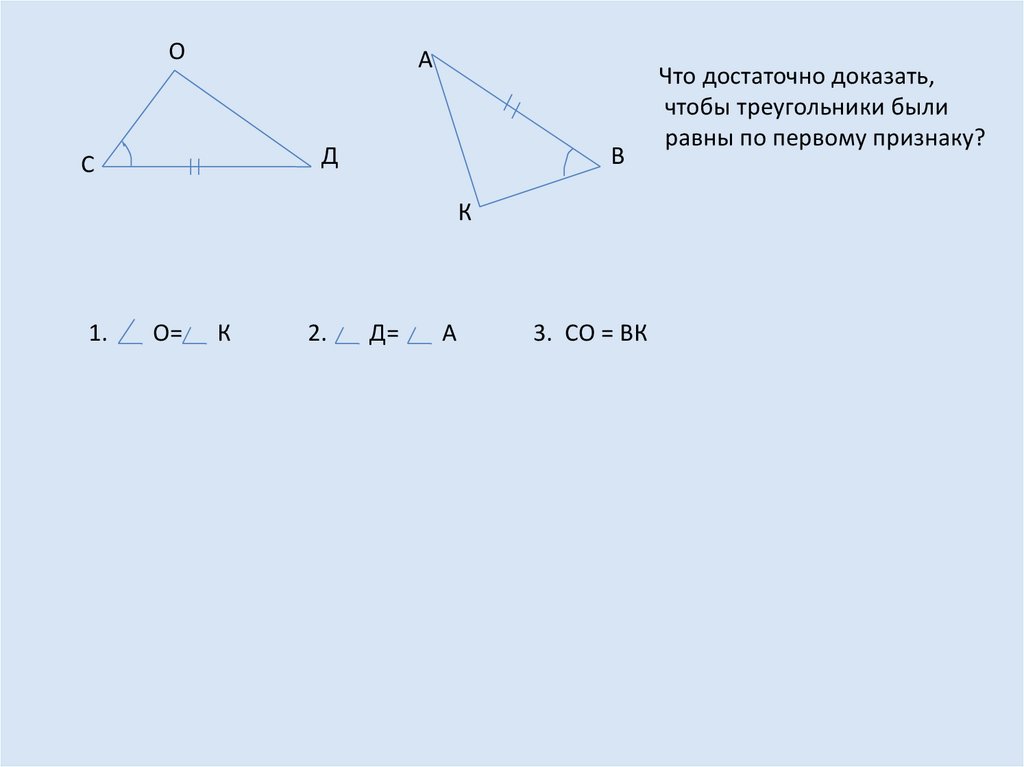
1.
О=
К
2.
Д=
А
3. СО = ВК
Что достаточно доказать,
чтобы треугольники были
равны по первому признаку?
10.
Решение задач поготовому рисунку
11.
ВС
О
А
Д
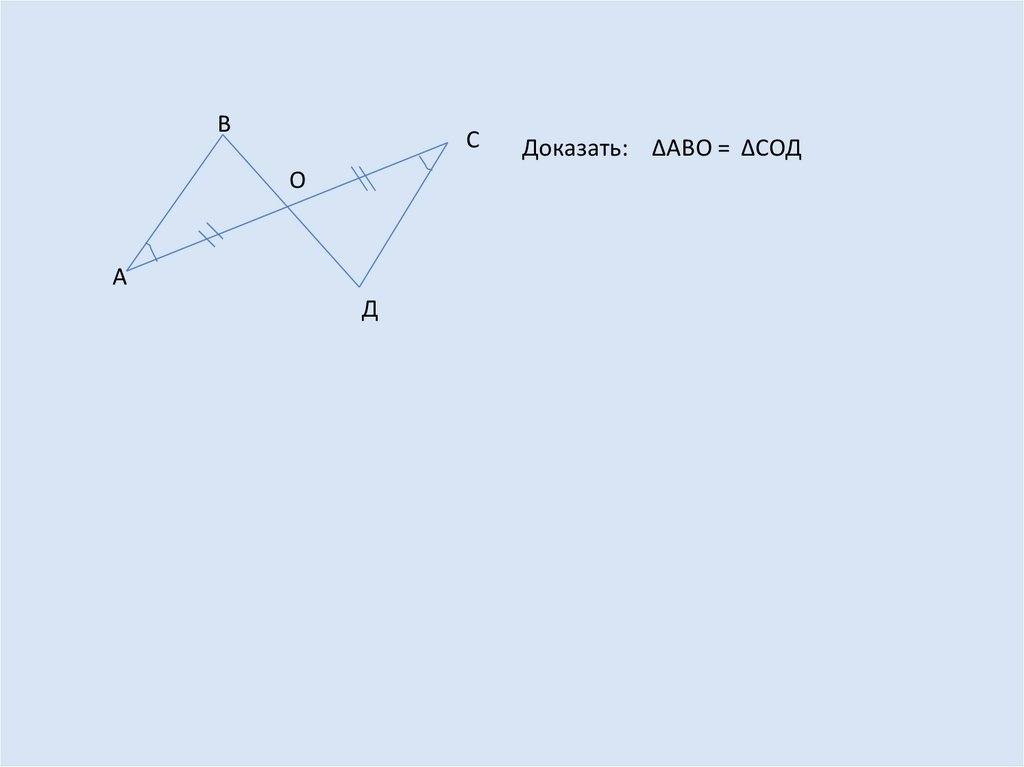
Доказать: ΔАВО = ΔСОД
12.
ЕС
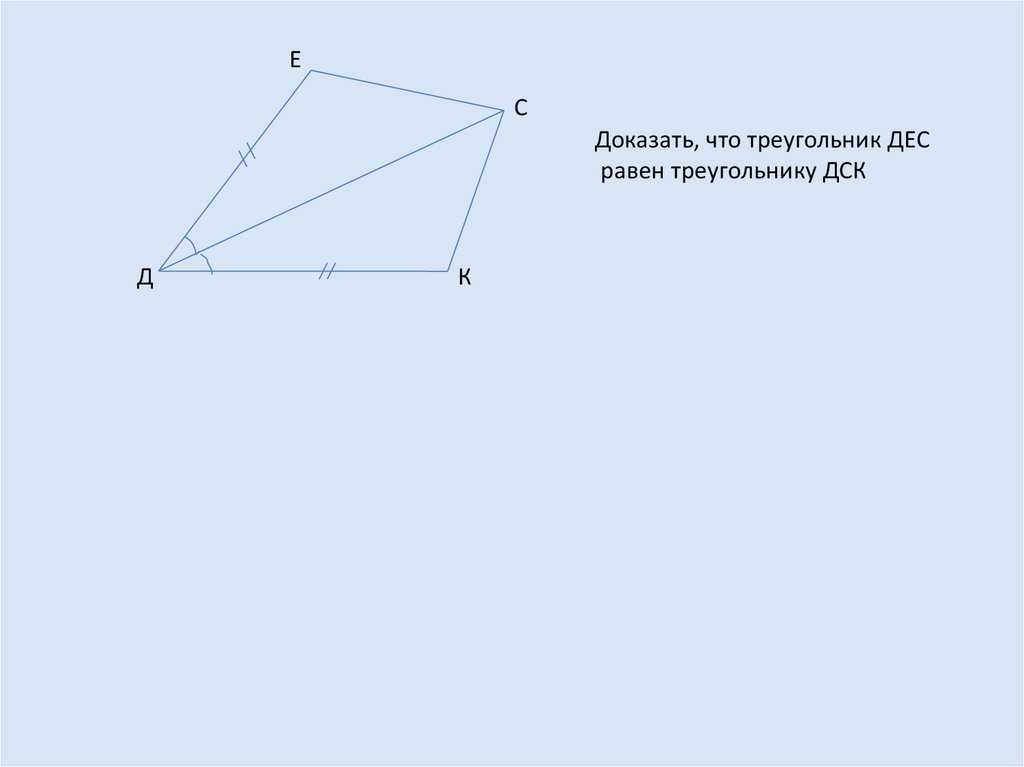
Доказать, что треугольник ДЕС
равен треугольнику ДСК
Д
К
13.
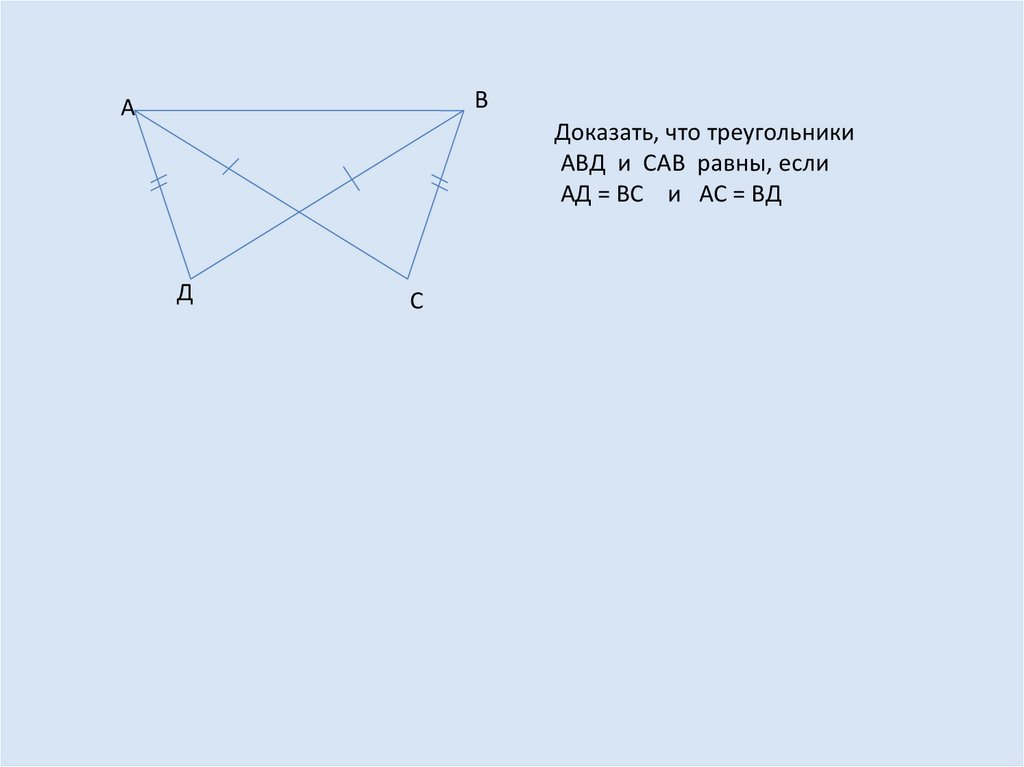
ВА
Доказать, что треугольники
АВД и САВ равны, если
АД = ВС и АС = ВД
Д
С
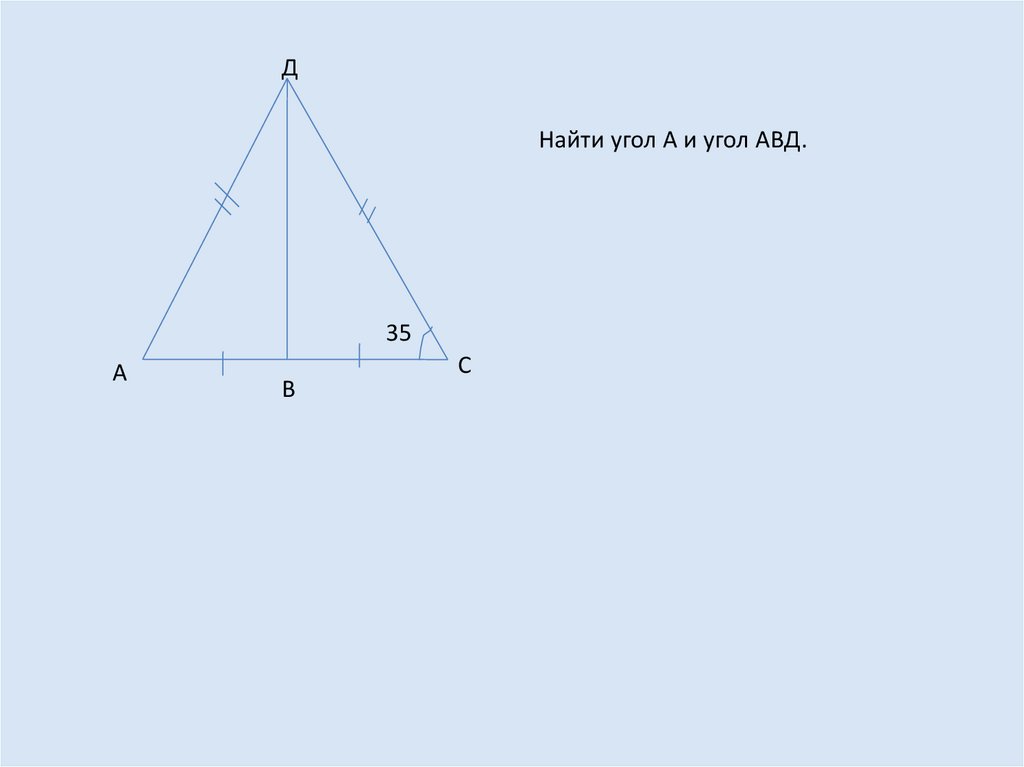
14.
ДНайти угол А и угол АВД.
35
А
В
С
15.
РЕШАЕМ ЗАДАЧИ16.
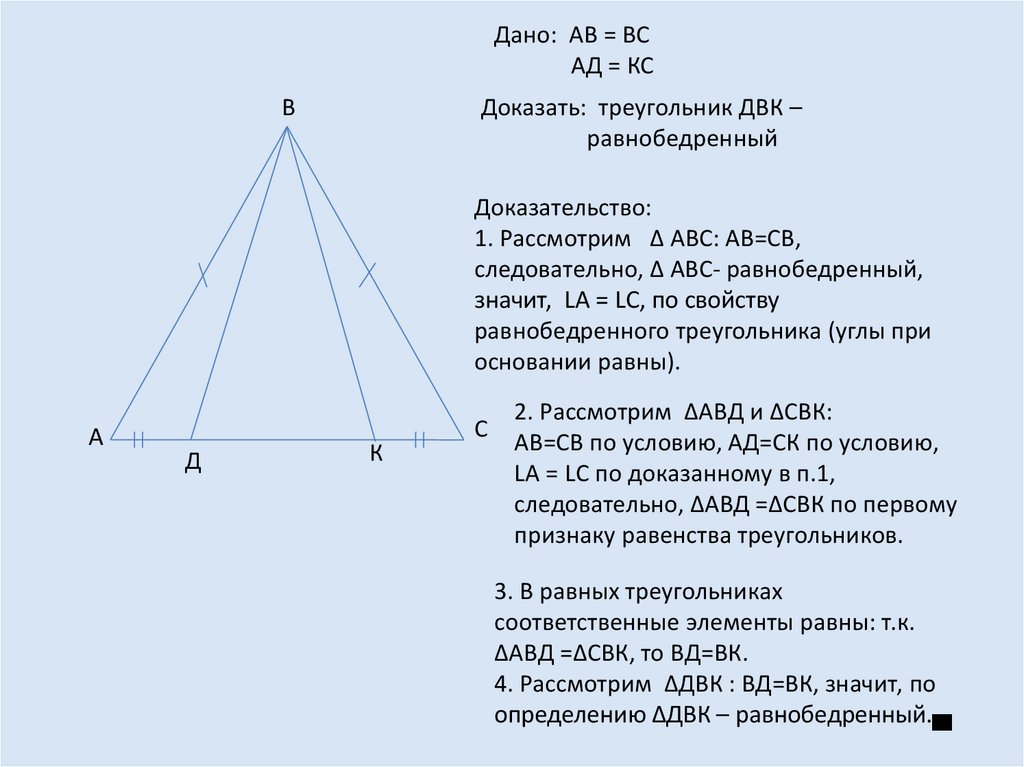
Дано: АВ = ВСАД = КС
В
Доказать: треугольник ДВК –
равнобедренный
Доказательство:
1. Рассмотрим Δ АВС: АВ=СВ,
следовательно, Δ АВС- равнобедренный,
значит, LА = LС, по свойству
равнобедренного треугольника (углы при
основании равны).
А
Д
К
С
2. Рассмотрим ΔАВД и ΔСВК:
АВ=СВ по условию, АД=СК по условию,
LА = LС по доказанному в п.1,
следовательно, ΔАВД =ΔСВК по первому
признаку равенства треугольников.
3. В равных треугольниках
соответственные элементы равны: т.к.
ΔАВД =ΔСВК, то ВД=ВК.
4. Рассмотрим ΔДВК : ВД=ВК, значит, по
определению ΔДВК – равнобедренный.▄
17.
ВВ1
Д
А
Д1
С
А1
С1
Дано: ΔАВС и ΔА1В1С1, АД и А1Д1 - биссектрисы АВ = А1В1, ВД = В1Д1, АД = А1Д1
Доказать: ΔАВС и ΔА1В1С1
Доказательство:
1. рассмотрим ΔАВД и ΔА1В1Д1: АВ=А1В1 по условию, ВД=В1Д1 по условию, АД=А1Д1 по
условию, следовательно, ΔАВД =ΔА1В1Д1 по трем сторонам, значит, LДАВ=LД1А1В1, L
В=LВ1.
2. Т.к. АД и А1Д1 – биссектрисы и LДАВ=LД1А1В1, то LВАС = LВ1А1С1.
3. Рассмотрим ΔАВС и ΔА1В1С1 : АВ = А1В1 по условию, LВ=LВ1 и
LВАС = LВ1А1С1 по доказанному ранее, следовательно, по второму признаку равенства
треугольников ΔАВС = ΔА1В1С1.▄
18.
«Если вы хотите научитьсяплавать, то смело входите
в воду,
а если хотите научиться
решать задачи,
то решайте их».
Д. Пойа.
19.
Дома: Повторить п.п. 14-20,Ответить устно на вопросы1-15
к гл.2 стр.48, подготовиться к
зачету.
Выполнить письменно №122,
138, 168, подготовиться к
контрольной работе.








 Математика
Математика








