Похожие презентации:
Средняя линия треугольника. Урок-исследование
1. Урок-исследование по теме «Средняя линия треугольника»
МатематикаУрок-исследование по
теме «Средняя линия
треугольника»
2.
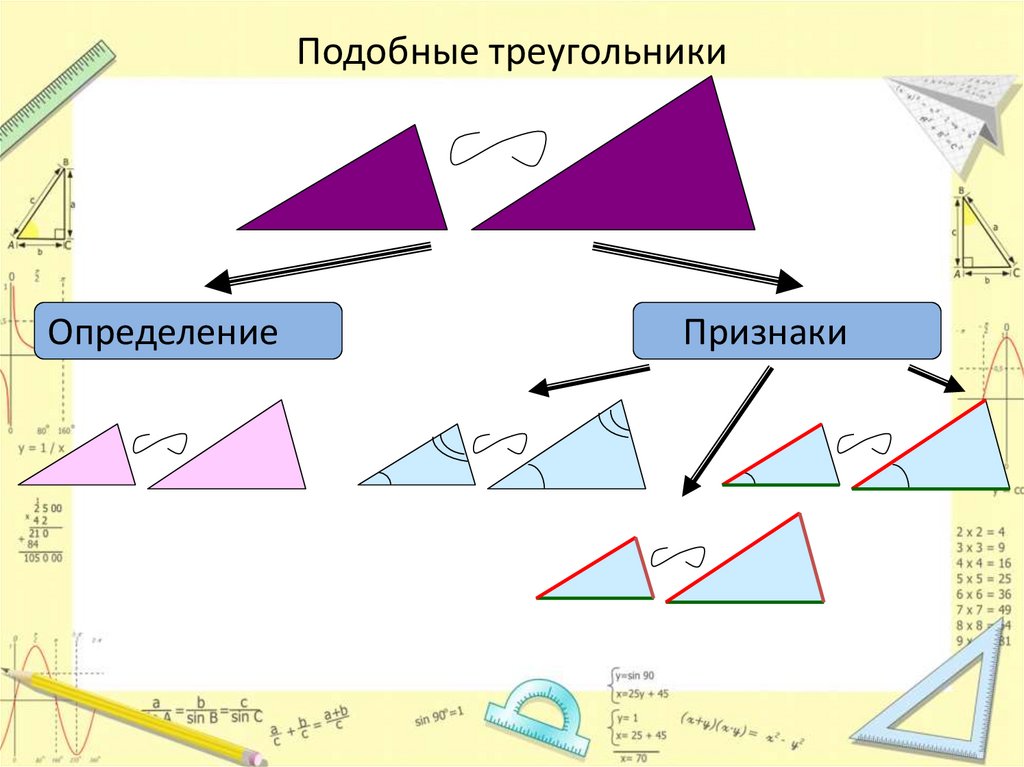
3. Подобные треугольники
ОпределениеПризнаки
4. Верно ли?
1. Два треугольника подобны, если ихуглы
равны и
стороны одного
треугольника
пропорциональны
сторонам другого.
5. Верно ли?
2. Два равносторонних треугольникавсегда подобны.
6. Верно ли?
3.Если
три
стороны
одного
треугольника
соответственно
пропорциональны трем сторонам
другого треугольника, то такие
треугольники подобны.
7. Верно ли?
4. Стороны одного треугольника имеютдлины 3, 4, 6 см, стороны другого
треугольника равны 9, 14, 18 см.
Подобны ли эти треугольники?
8. Верно ли?
5. Периметры подобных треугольниковотносятся как квадраты сходственных
сторон.
9. Верно ли?
6. Если два угла одного треугольникаравны 60 и 50 , а два угла другого
треугольника равны 50 и 70 , то
такие треугольники подобны.
10. Верно ли?
7. Два прямоугольных треугольникаподобны, если имеют по равному
острому углу.
11. Верно ли?
8. Отношение площадей подобныхтреугольников
равно
квадрату
коэффициента подобия.
12.
13.
С4
D
С
5
Е
8
А
D
6
CD II AB
О
10
В
А
4
В
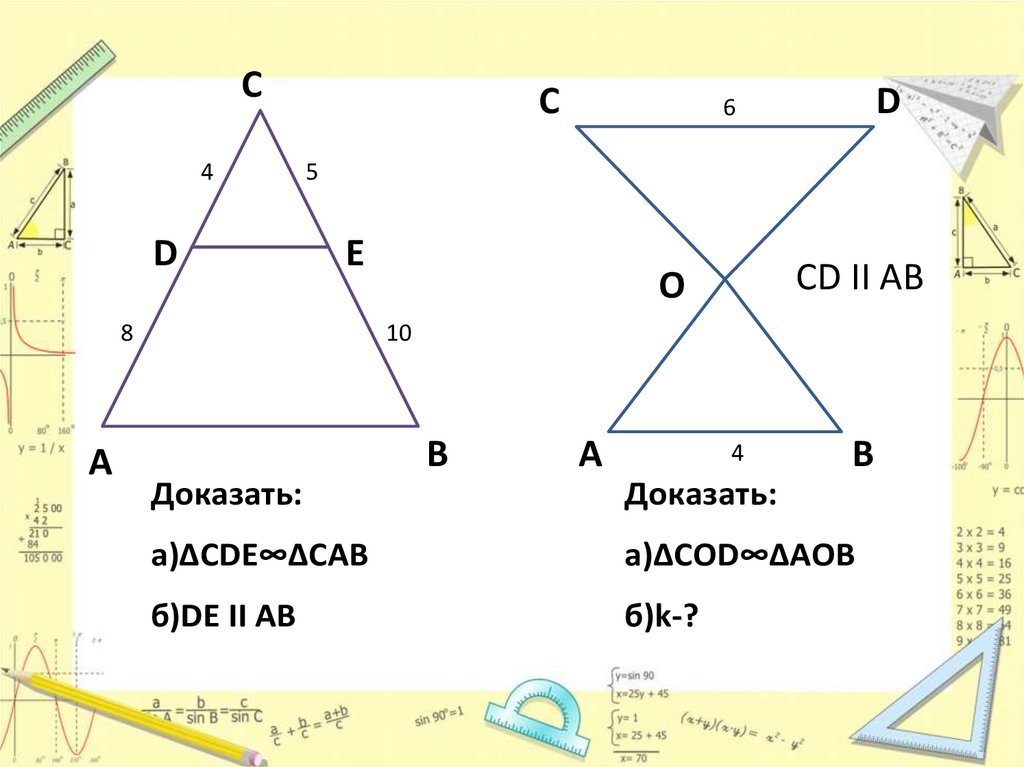
Доказать:
Доказать:
а)ΔCDE∞ΔCAB
а)ΔCOD∞ΔAOB
б)DE II AB
б)k-?
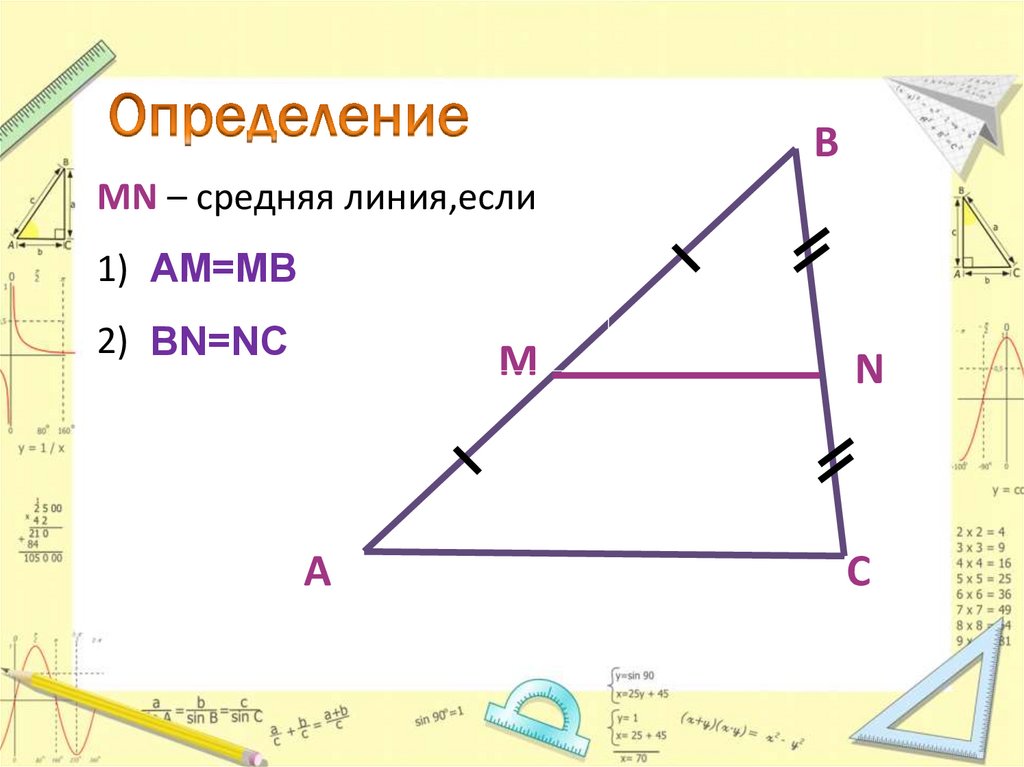
14. Определение
ВMN – средняя линия,если
1) АМ=МВ
2) ВN=NC
М
А
N
С
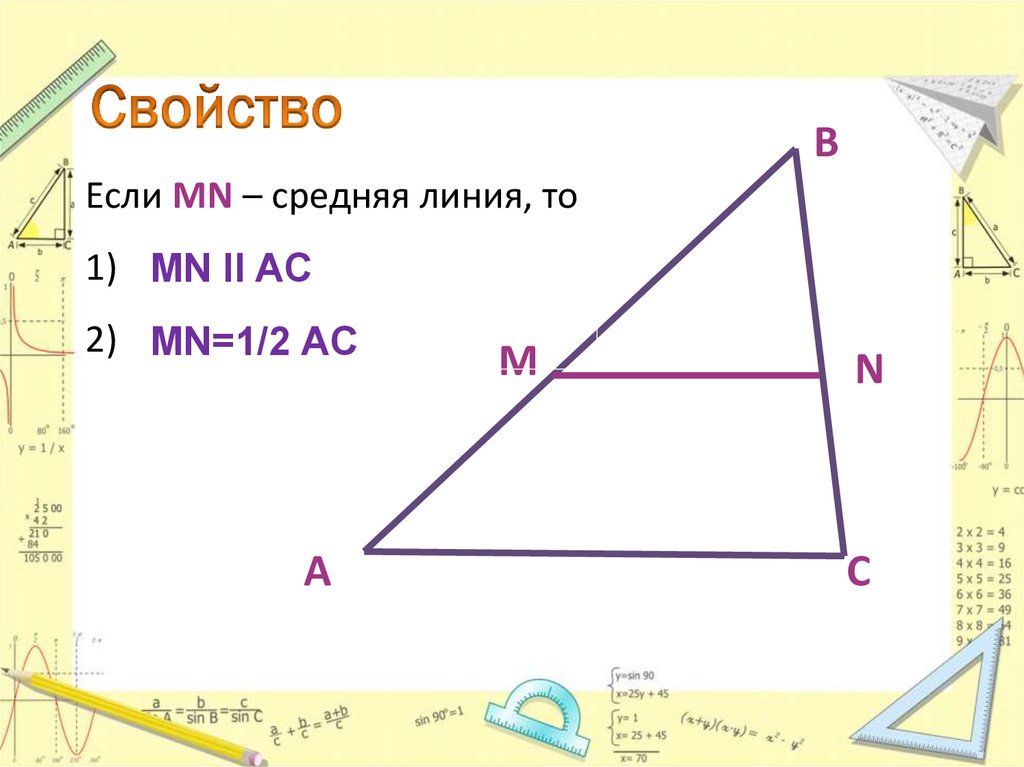
15. Свойство
ВЕсли MN – средняя линия, то
1) MN II AC
2) MN=1/2 AC
А
М
N
С
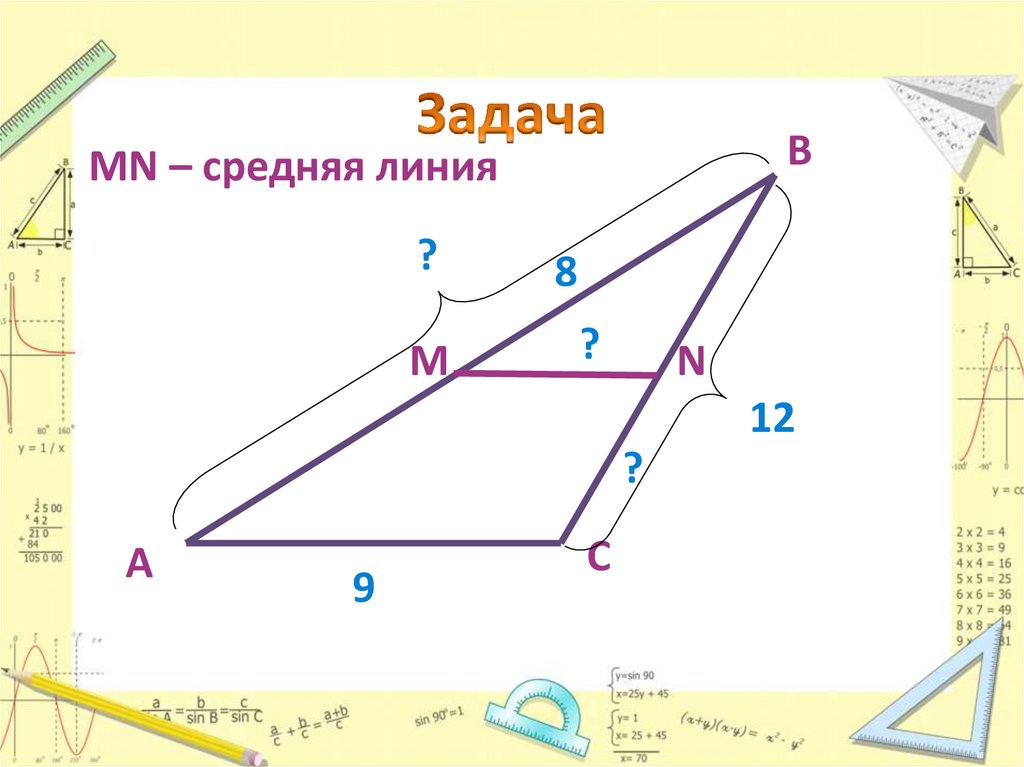
16. Задача
ВМN – средняя линия
?
М
8
?
N
12
?
А
9
С
17. Задача
ВА
С
18.
ВМN - средняя линия
МК - средняя линия
КN - средняя линия
М
А
К
N
С
19.
ВВ
KN=
8
М
N
5
A
К
MN=
20
BC=
М
MK=
4
AC=
4
С
A
В
К
BC=
М
5
3
A
7
N
AC=
AB=
MK=
К
N
7
AB=
С
KN=
KN=
С
BC=
AC=
AM=
20.
ВВ
KN=8
8
М
N
5
A
К
MN=4
20
BC=10
М
MK=7
4
AC=8
С
4
A
В
7
М
5
N
3
A
К
BC=14
AC=10
AB=6
МК=7
К
N
7
AB=16
С
КN=3
KN=10
С
BC=14
AC=8
AM=10
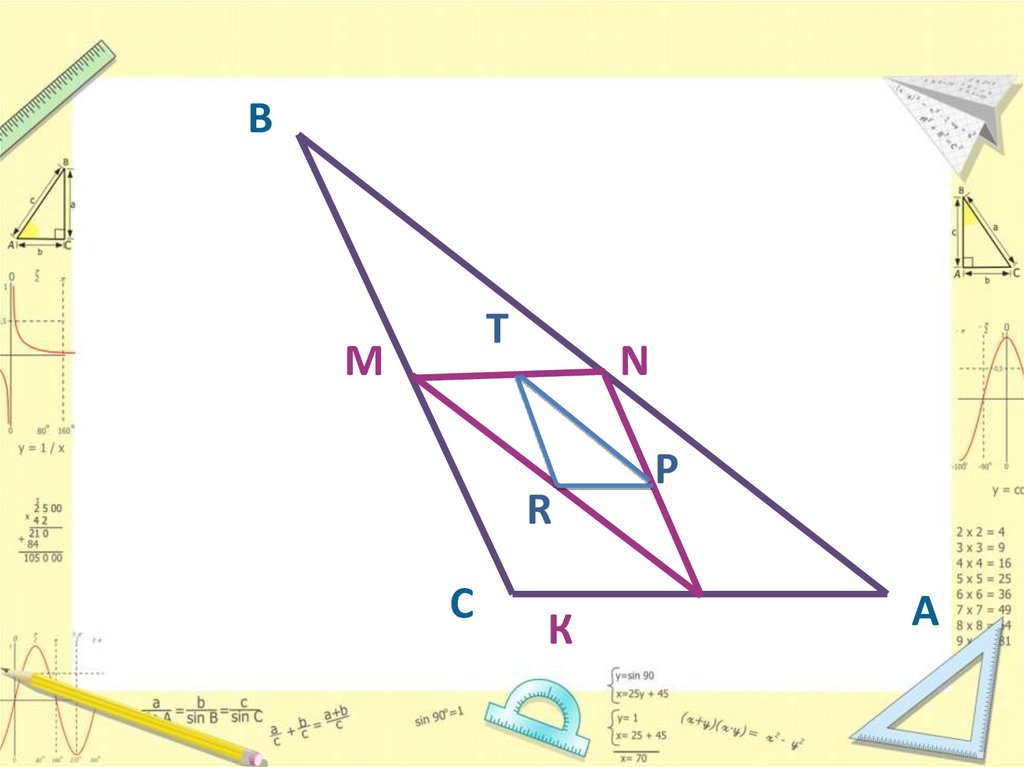
21.
ВT
М
N
R
С
К
P
А
22.
ТестТема: Средняя линия треугольника.
1) Если MN-средняя линия треугольника, параллельная основанию, равному 8 см, то
MN равно:
а) 16;
б) 12;
в)4.
2) В равностороннем треугольнике все средние линии имеют одинаковую длину:
а) да;
б) нет;
в) не всегда.
3) В треугольнике ABC: AB=6, BC=12, AC=8, M-середина BC,
K-середина AC. Найдите длину MK.
а) 3;
б) 4;
в) 6.
4) Средняя линия равнобедренного треугольника, параллельная основанию, равна 2
см, а его периметр равен 18 см.
Найдите стороны треугольника.
а)1; 8,5; 8,5; б) 4; 7; 7; в) 4; 4; 10.
5) В треугольнике ABC проведена средняя линия FE , параллельная AC. Определите
периметр треугольника FBE, если
периметр треугольника ABC равен 18 см.
а) 15 ;
б) 36;
в) 9.
Дополнительная часть
6) Диагональ квадрата равна 12 см. Найдите периметр четырёхугольника,
образованного отрезками, которые последовательно соединяют середины сторон
данного квадрата.
а)24;
б) 48;
в) 36.
7) Дано: ABCD- квадрат, M, N, P, Q – середины сторон.
Укажите вид четырёхугольника MNPQ.
а) параллелограмм; б) квадрат; в) ромб.
23.
12
3
4
5
6
7
в
а
а
б
в
а
б



















 Математика
Математика








