Первый признак равенства треугольников

1.

Первый признак
равенства треугольников

2.

Треугольник
А
В
РАВС = АВ + ВС + СА
С
Точки А, В, С – вершины треугольника.
Отрезки АВ, ВС и СА – стороны треугольника.
Обозначают: ∆ АВС, ∆ ВСА, ∆ САВ.
∠ ВАС, ∠ СВА, ∠ АСВ – углы ∆ АВС,
( ∠ А, ∠ В, ∠ С ).

3.

В1
В
А
С
А1
С1
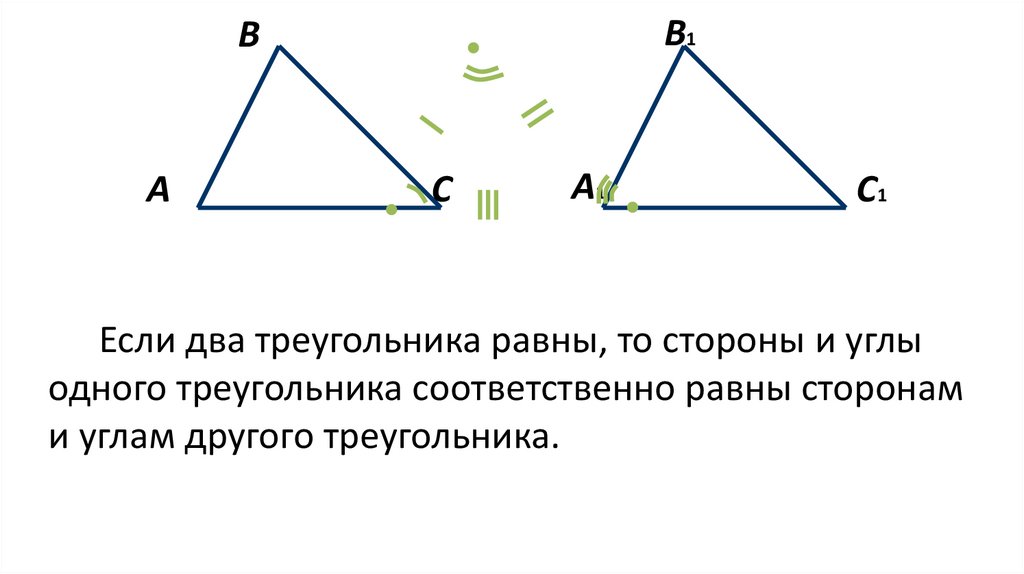
Если два треугольника равны, то стороны и углы
одного треугольника соответственно равны сторонам
и углам другого треугольника.

4.

В равных треугольниках против соответственно
равных сторон лежат равные углы, и наоборот: против
соответственно равных углов лежат равные стороны.
В
А
В1
С
А1
Обозначают: ∆ АВС = ∆ А1В1С1
С1

5.

Теорема – это утверждение, справедливость
которого устанавливается путём рассуждений.
Рассуждения называются доказательством
теоремы.

6.

Первый признак равенства
треугольников
Если две стороны и угол между ними
одного треугольника соответственно равны
двум сторонам и углу между ними другого
треугольника, то такие треугольники равны.

7.

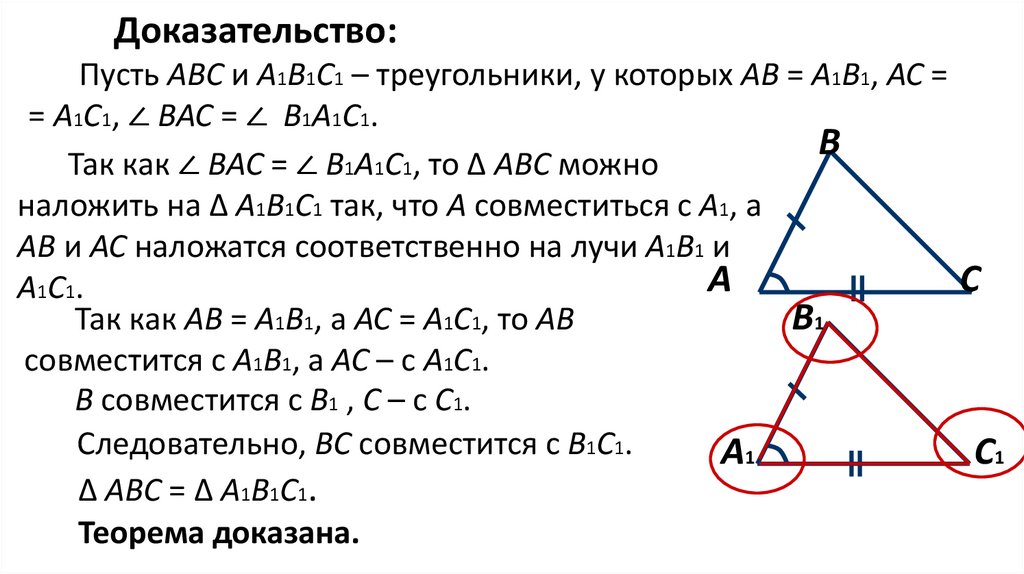
Доказательство:
Пусть АВС и А1В1С1 – треугольники, у которых АВ = А1В1, АС =
= А1С1, ∠ ВАС = ∠ В1А1С1.
В
Так как ∠ ВАС = ∠ В1А1С1, то ∆ АВС можно
наложить на ∆ А1В1С1 так, что А совместиться с А1, а
АВ и АС наложатся соответственно на лучи А1В1 и
А
С
А1С1.
Так как АВ = А1В1, а АС = А1С1, то АВ
В1
совместится с А1В1, а АС – с А1С1.
В совместится с В1 , С – с С1.
Следовательно, ВС совместится с В1С1.
А1
С1
∆ АВС = ∆ А1В1С1.
Теорема доказана.

8.

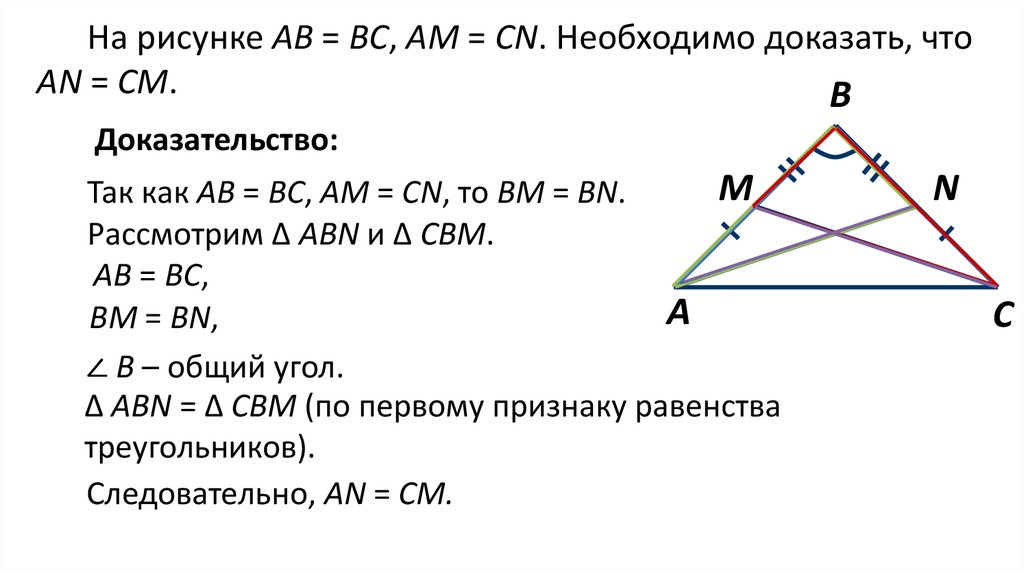
На рисунке АВ = ВС, АМ = CN. Необходимо доказать, что
АN = СМ.
В
Доказательство:
M
Так как АВ = ВС, АМ = CN, то BM = BN.
Рассмотрим ∆ ABN и ∆ СВМ.
АВ = ВС,
А
ВМ = BN,
∠ В – общий угол.
∆ ABN = ∆ СВМ (по первому признаку равенства
треугольников).
Следовательно, АN = СМ.
N
С