Синус, косинус и тангенс острого угла прямоугольного треугольника. Решение прикладных задач

1. МОУСОШ № 50 г. Воронеж

Тема урока:
«Синус, косинус и тангенс
острого угла прямоугольного
треугольника»
Учитель математики Крынина Светлана Ивановна

2.

Цели урока.
Образовательные:
формировать понятия синуса, косинуса и тангенса острого угла
прямоугольного треугольника;
Развивающие:
развивать способности к самостоятельному планированию и
организации работы; навыки коррекции собственной деятельности
через применение информационных технологий; умение обобщать,
абстрагировать и конкретизировать знания
Воспитательные:
воспитывать познавательный интерес к математике,
информационную культуру и культуру общения, самостоятельность,
способность к коллективной работе.

3.

Актуализация ЗУН, необходимых для творческого
применения знаний
Математический диктант
1. Назовите стороны треугольника МРК.
2. Чему равна сумма углов треугольника?
3. Сформулировать теорему о соотношениях между
сторонами и углами треугольника.
4. Сформулировать следствие о величине
гипотенузы и катета в прямоугольном
треугольнике.
5. Сформулировать свойство катета прямоугольного
треугольника, лежащего против угла 30°.

4. Пусть АВС – прямоугольный треугольник с прямым углом С и острым углом при вершине А, равным

Изучение нового материала
Пусть АВС – прямоугольный
треугольник с прямым углом С и острым
углом при вершине А, равным
В
С
А

5.

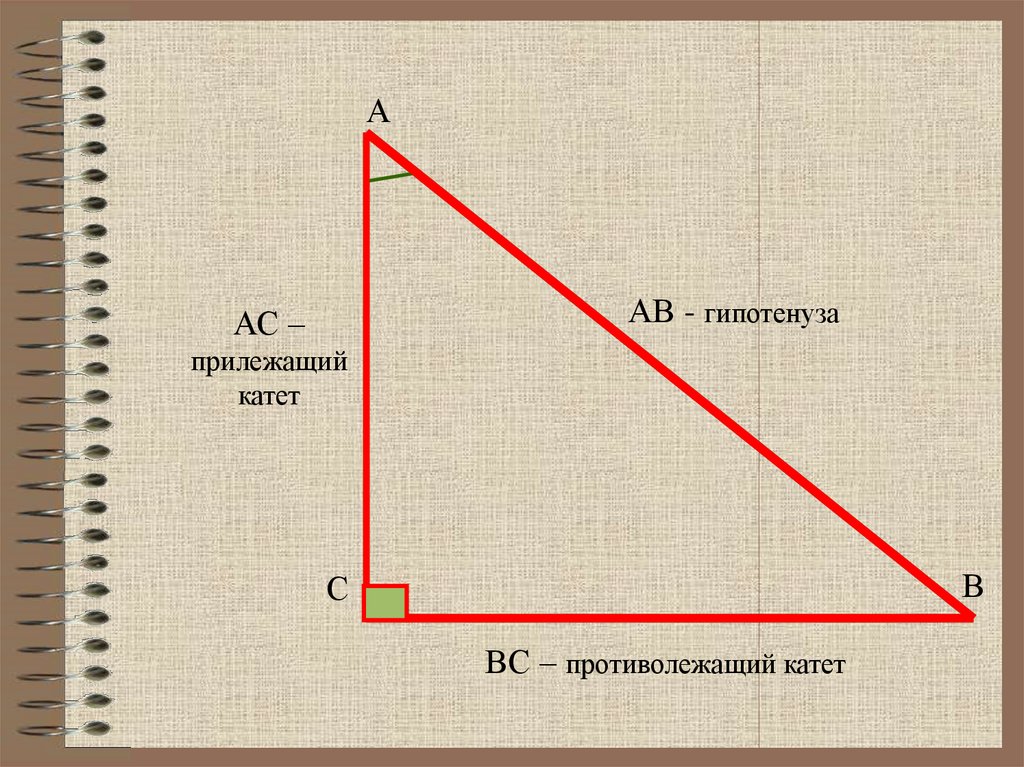
А
АВ - гипотенуза
АС –
прилежащий
катет
В
С
ВС – противолежащий катет

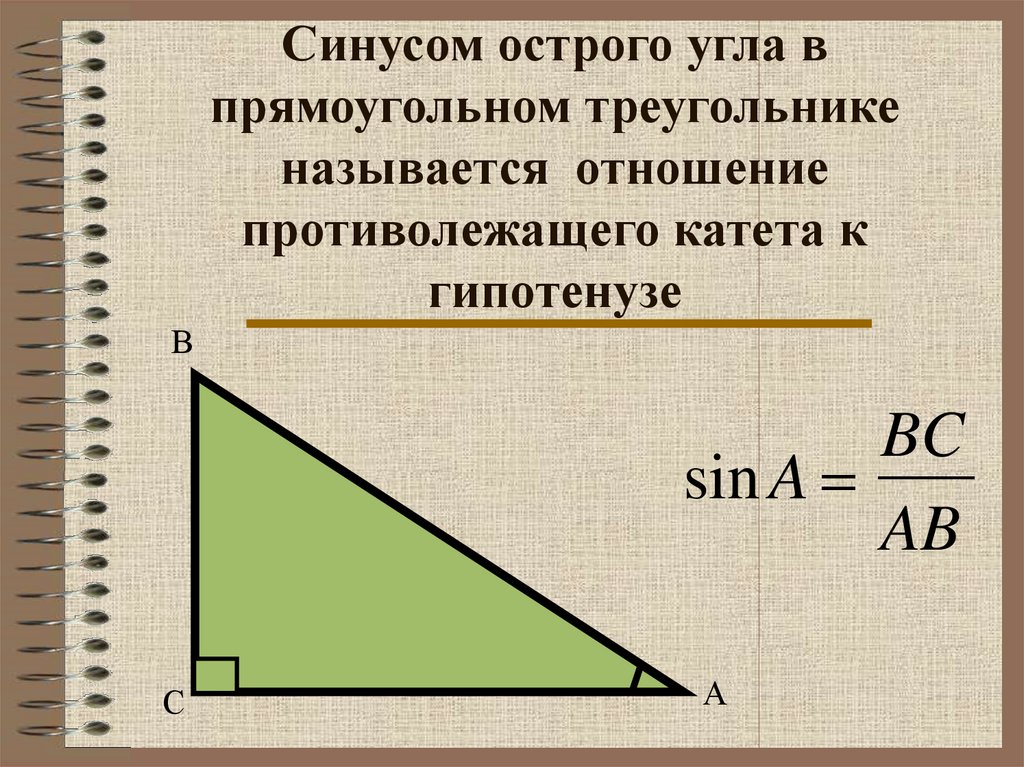
6. Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе

В
BC
sin A =
AB
С
А

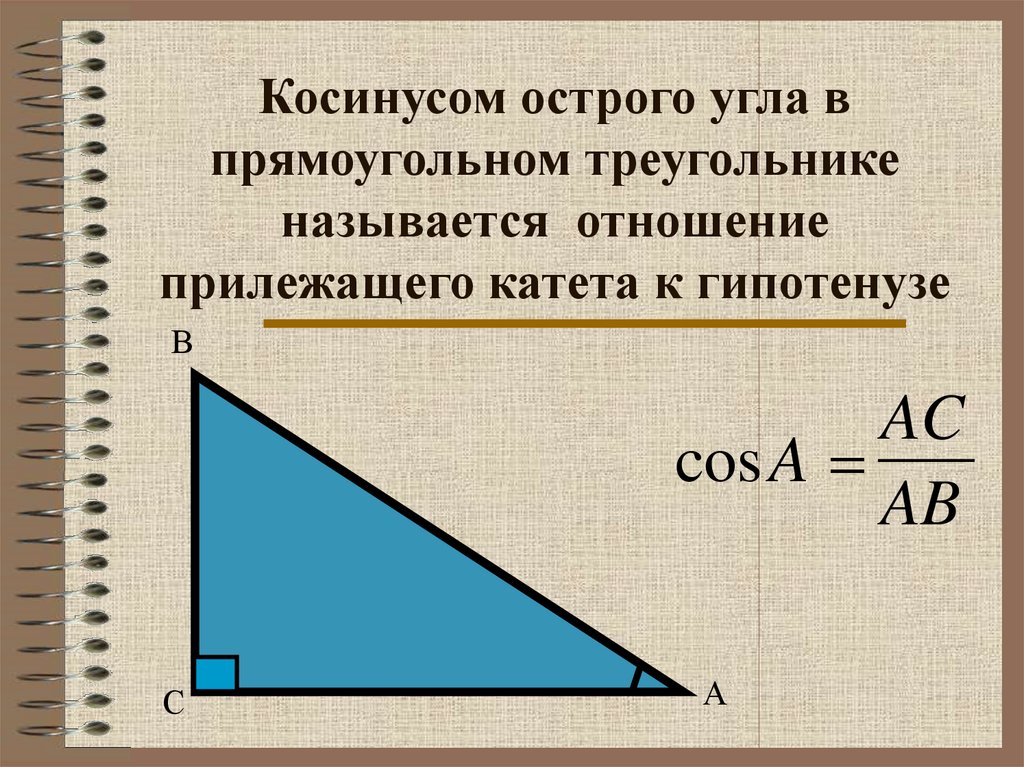
7. Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе

В
AC
cos A =
AB
С
А

8. Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему

В
BC
tg A =
AC
С
А

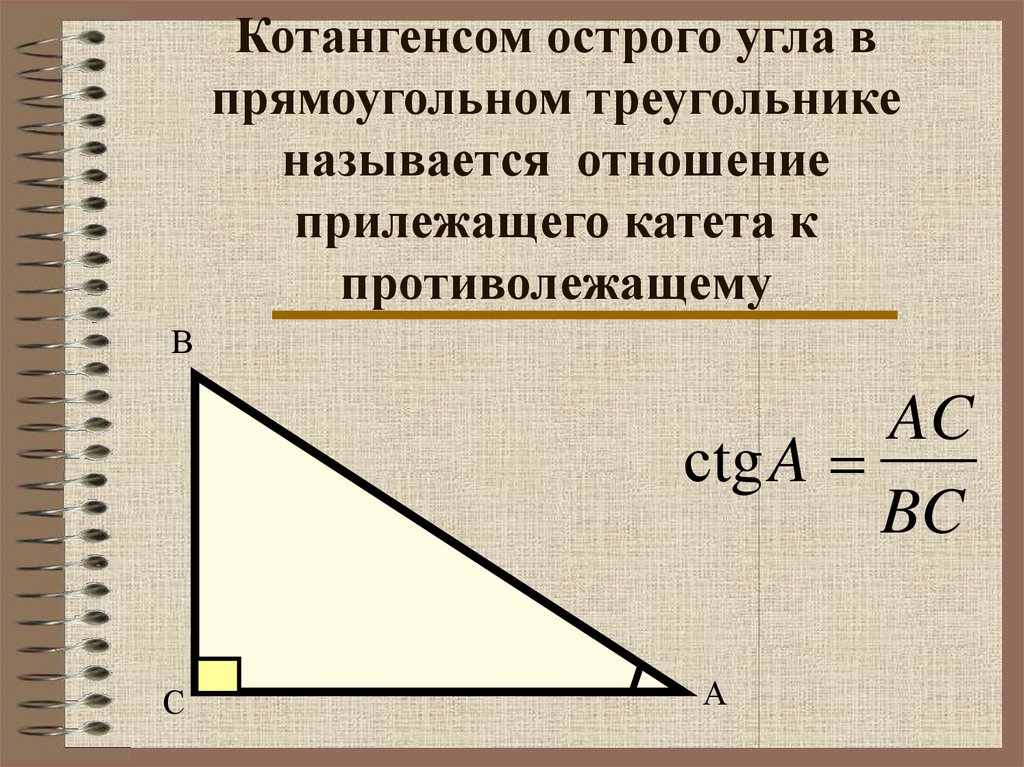
9. Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему

В
AC
сtgA =
BC
С
А

10. Эти правила позволяют , зная одну из сторон прямоугольного треугольника и острый угол , находить две другие стороны; зная две

стороны,
находить острые углы

11.

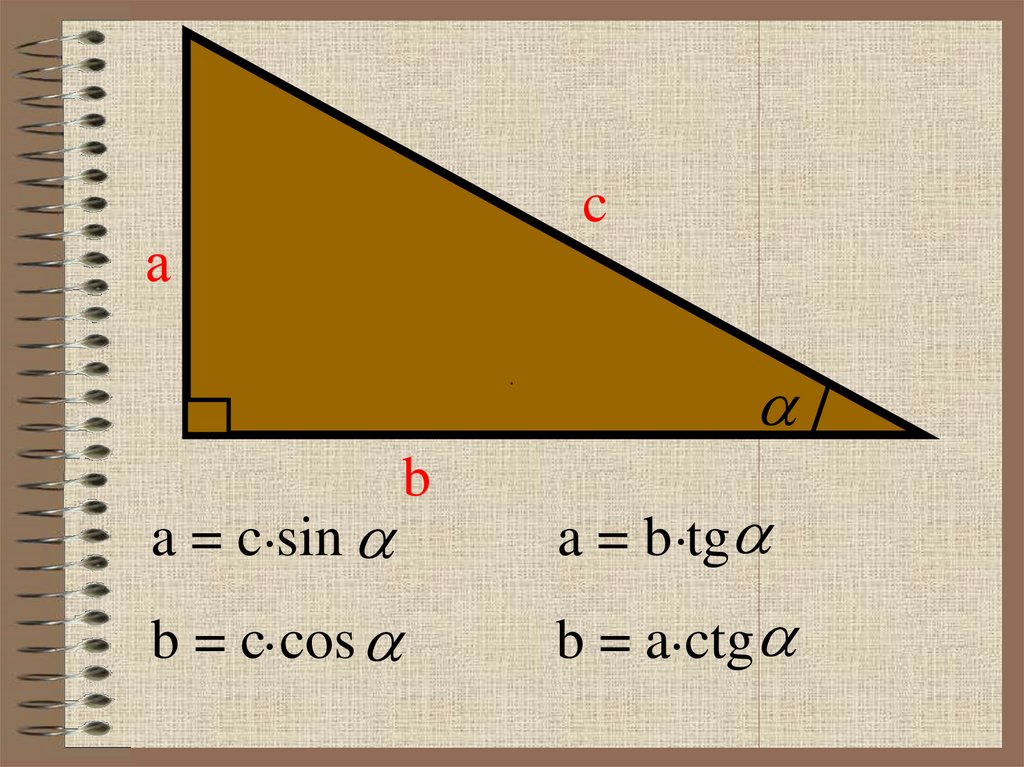
c
а
a = c sin
b = c cos
b
a = b tg
b = a ctg

12. Основное тригонометрическое тождество

Используя формулы синуса и косинуса получаем
BC
AC
BC AC
sin A cos A =
=
2
2
AB
AB
AB 2
2
2
2
2
2
2
2
2
BC
AC
=
AB
по теореме Пифагора
отсюда следует
sin2A + cos2A = 1
2

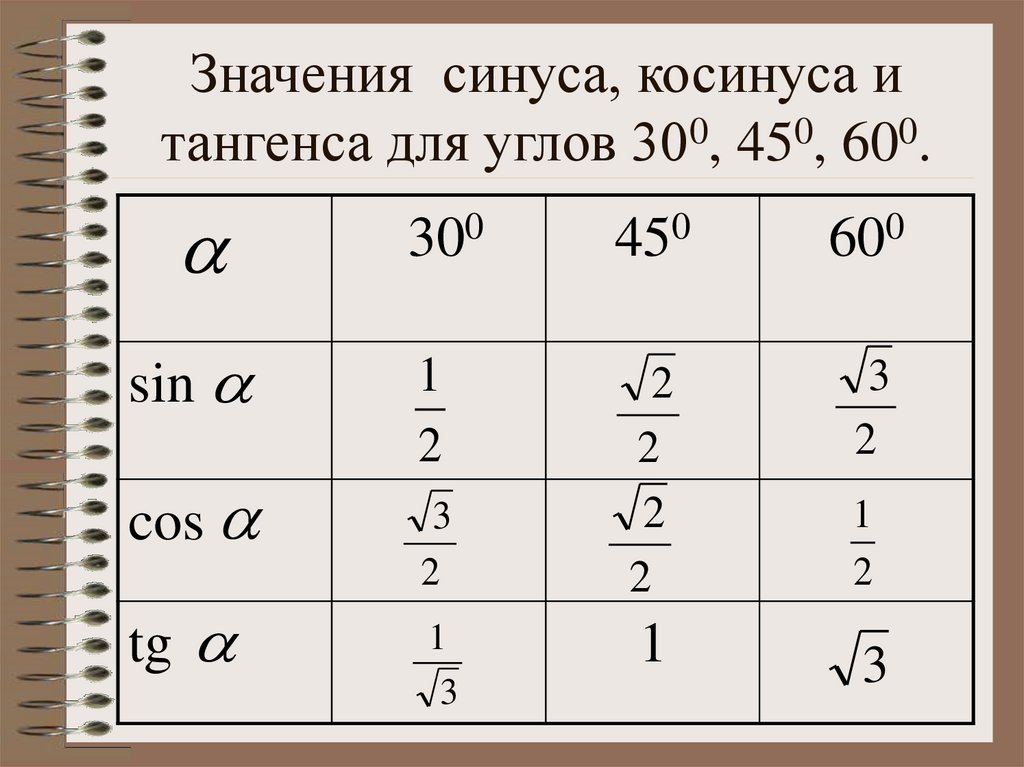
13. Значения синуса, косинуса и тангенса для углов 300, 450, 600.

sin
cos
tg
300
1
2
3
2
1
3
450
600
2
2
2
2
3
2
1
2
1
3

14.

Творческая работа

15. З а д а ч а

Задача
В прямоугольном треугольнике
даны гипотенуза с и острый
угол α. Найти катеты, их
проекции на гипотенузу и
высоту, опущенную на
гипотенузу.

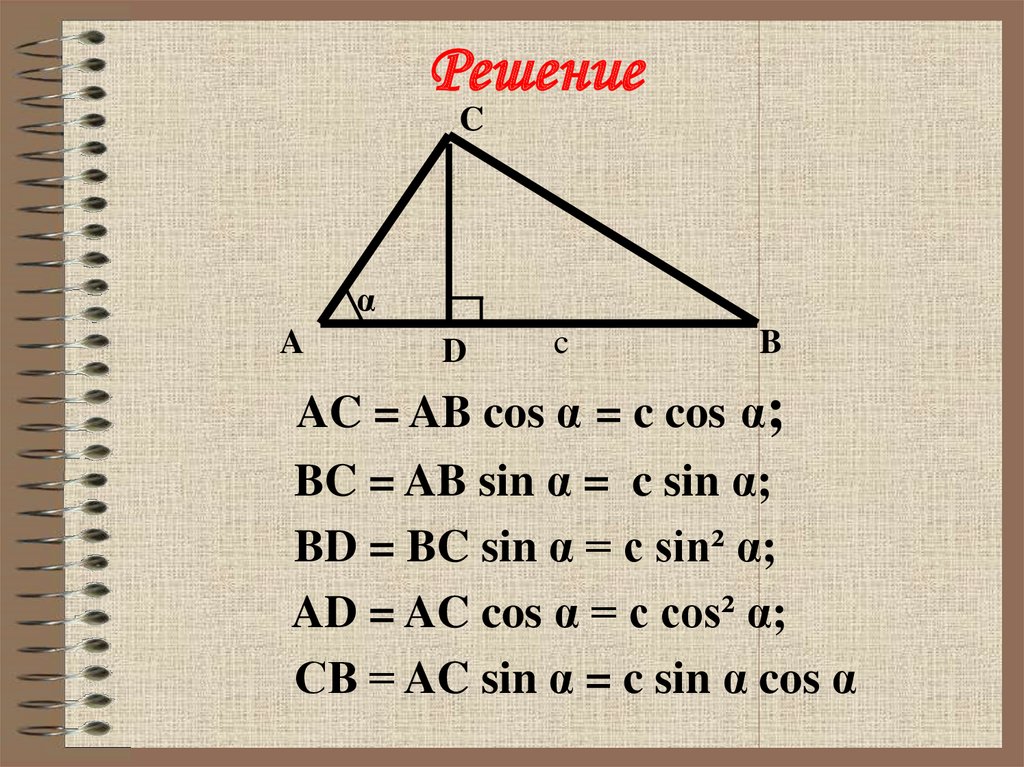
16. Решение

C
α
A
D
c
B
AC = AB cos α = c cos α;
BC = AB sin α = c sin α;
BD = BC sin α = c sin² α;
AD = AC cos α = c cos² α;
СВ = AC sin α = c sin α cos α

17.

III. Закрепление изученного материала
Решение прикладных задач

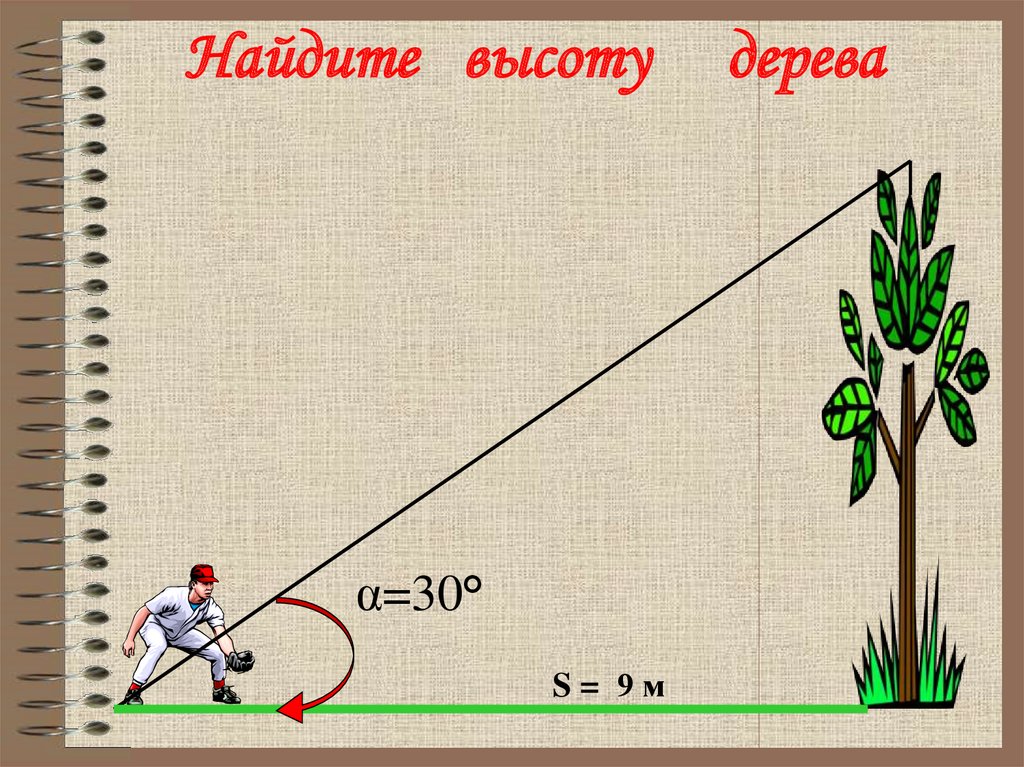
18. Найдите высоту дерева

Найдите высоту
α=30°
S= 9м
дерева

19. Найдите угол наклона Пизанской башни

h 1 = 60 м
21
h 2 = 50 м
α=?

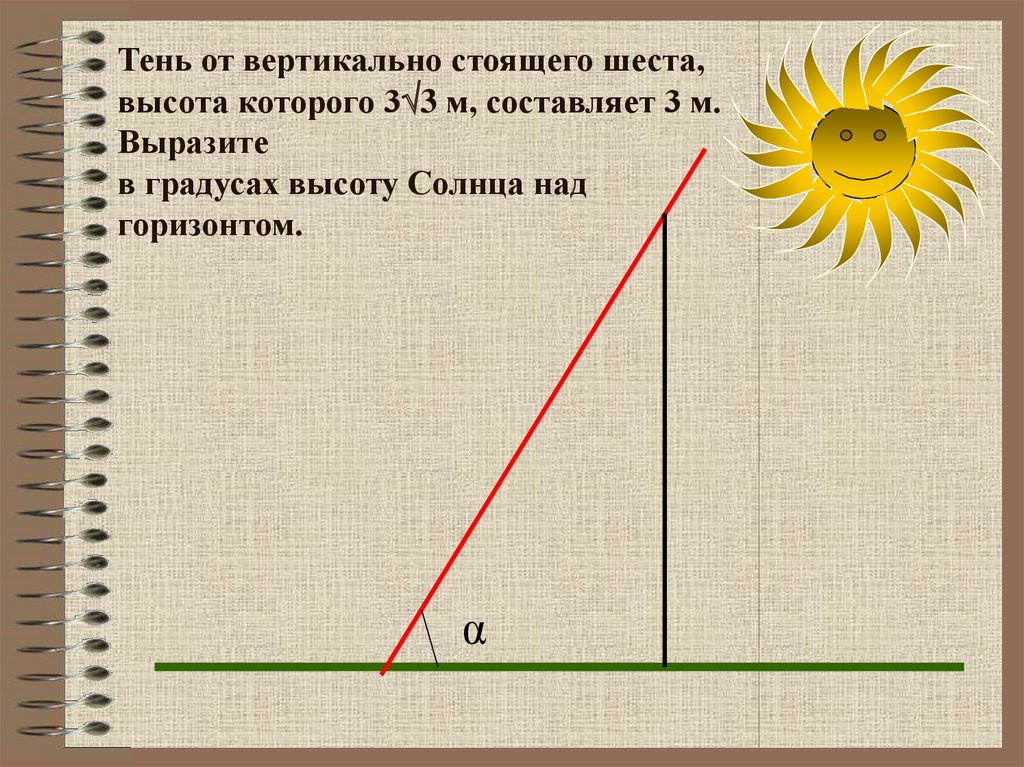
20. Тень от вертикально стоящего шеста, высота которого 33 м, составляет 3 м. Выразите в градусах высоту Солнца над горизонтом.

Тень от вертикально стоящего шеста,
высота которого 3 3 м, составляет 3 м.
Выразите
в градусах высоту Солнца над
горизонтом.
α

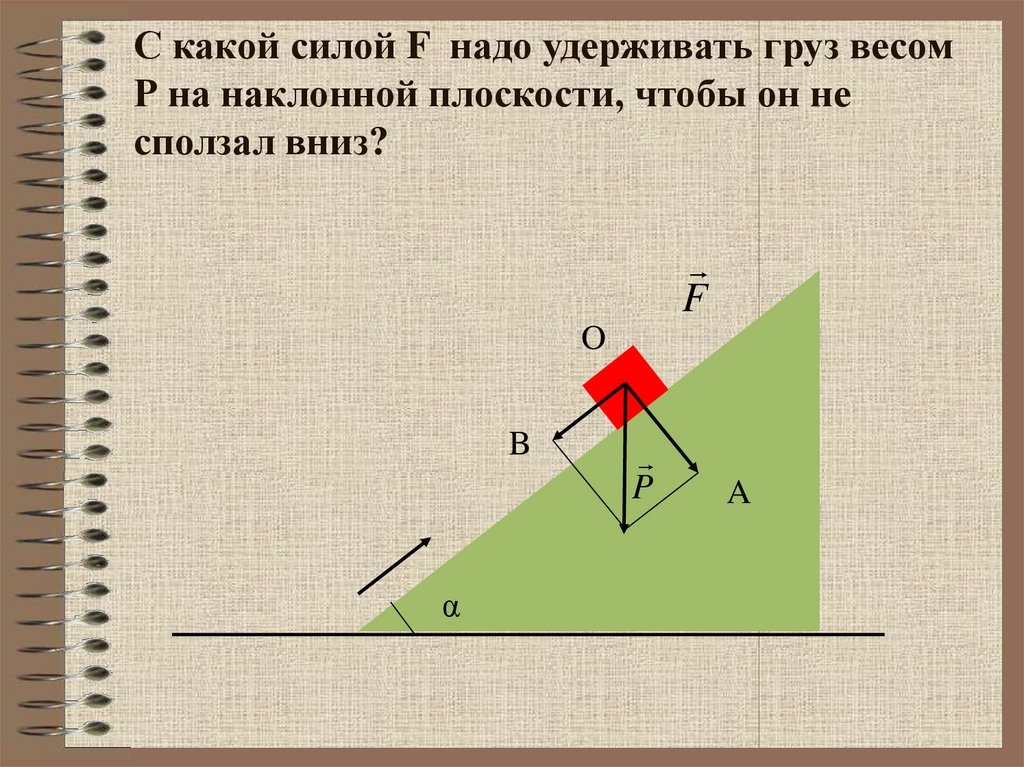
21. С какой силой F надо удерживать груз весом Р на наклонной плоскости, чтобы он не сползал вниз?

F
O
B
α
P
A

22.

Решение.
Пусть О – центр тяжести груза,
к
Р
которому
приложена
сила
.
Разложим
вектор Р по двум взаимно
перпендикулярным направлениям, как
показано на рисунке. Сила ОА
перпендикулярна наклонной плоскости
и не вызывает перемещения груза. Сила
F , удерживающая груз, должна быть
равной по величине и противоположной
по направлению силе ОВ . Поэтому
F = P sin α

23.

А
60°
С
В
Р
Груз Р массой 1 т
поддерживается
двумя стержнями
АВ и ВС,
прикрепленными к
стене при помощи
шарниров.
Определите силу
действующую на
стержни, если
САВ = 90 , а
АСВ= 60 .

24.

Кроссворд

25. Информационные материалы.

• Пифагор. Занимательная математика. Халамайзер А.Я.
Москва
• «Высшая школа» 1994г.
• Живая математика. Перельман Я. И. Москва «Наука» 1978 г.
• Интеллектуальный пир. Серия «Клуб эрудитов» Выпуск 2.
Кострома ИМЦ «Вариант» 1993 г.
• Коллекция 80000 анимаций. - www.animashky.ru
• Большая энциклопедия Кирилла и Мефодия, 8 CD-ROM,
2002 г.
• Электронные ресурсы сайта «Сеть творческих учителей»
• Электронные ресурсы сайта «Фестиваль педагогических идей
«Открытый урок»
• Учебное электронное пособие «Математика 5-11», Дрофа
• Учебно-методическое пособие. Взаимосвязь теории с
практикой в процессе изучения математики. Возняк Г.М.,
Маланюк М.П. Киев. «Радянська школа»