Перпендикулярность в пространстве

1.

Урок № 18
a b
Перпендикулярность в
пространстве
a
План урока:
1 Повторяем теорию.
2 Изучаем новый материал.
3 Записываем ДЗ.
Двугранный угол.
Перпендикулярность плоскостей

2.

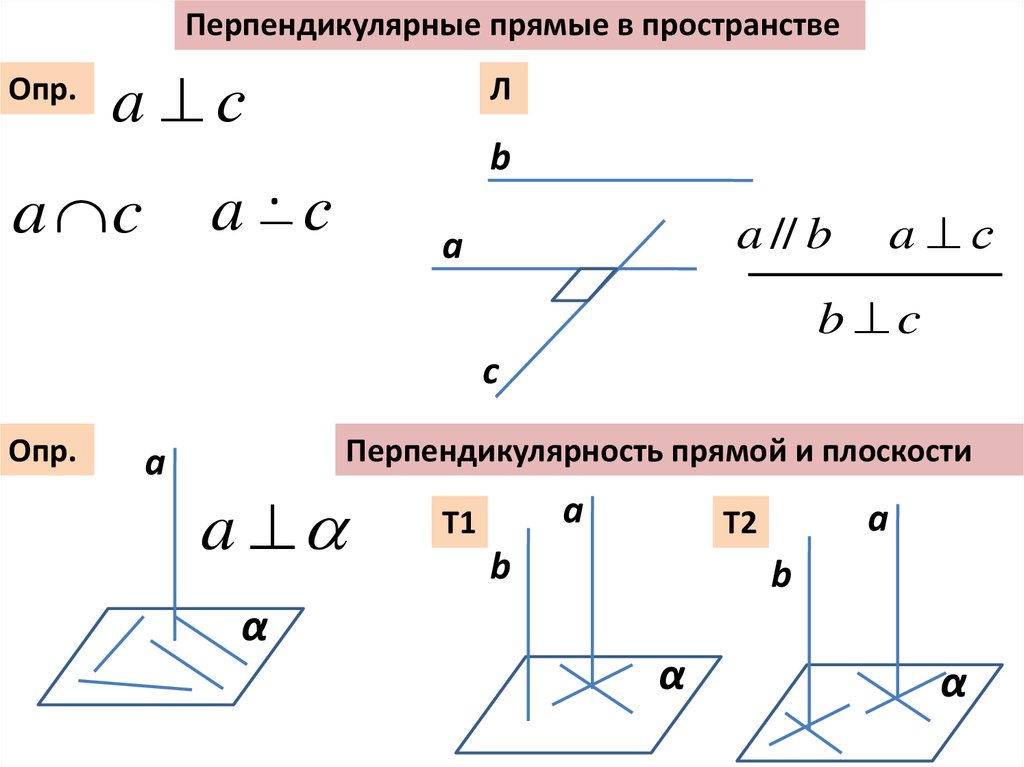
Перпендикулярные прямые в пространстве
Опр.
a с
a c
Л
b
a·с
a // b
a
a с
b c
c
Опр.
a
Перпендикулярность прямой и плоскости
a
a
Т1
a
Т2
b
b
α
α
α

3.

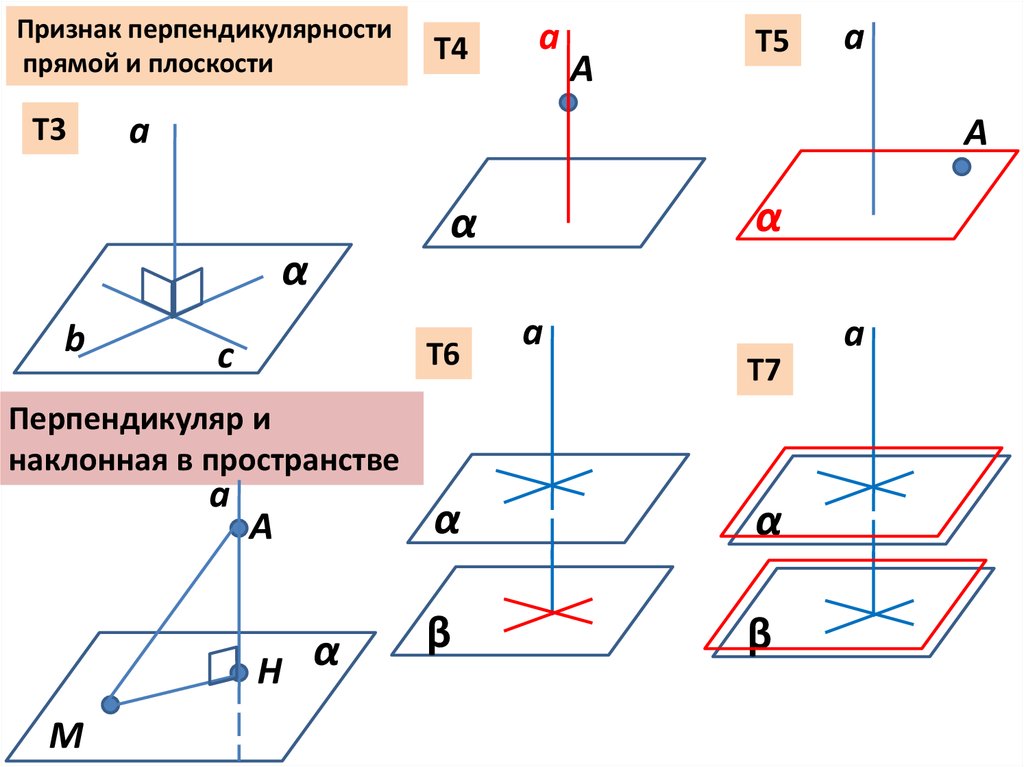
Признак перпендикулярности
прямой и плоскости
Т3
Т4
a
А
Т5
a
a
А
α
α
α
b
с
Т6
a
Т7
Перпендикуляр и
наклонная в пространстве
a
М
А
α
α
Н α
β
β
a

4.

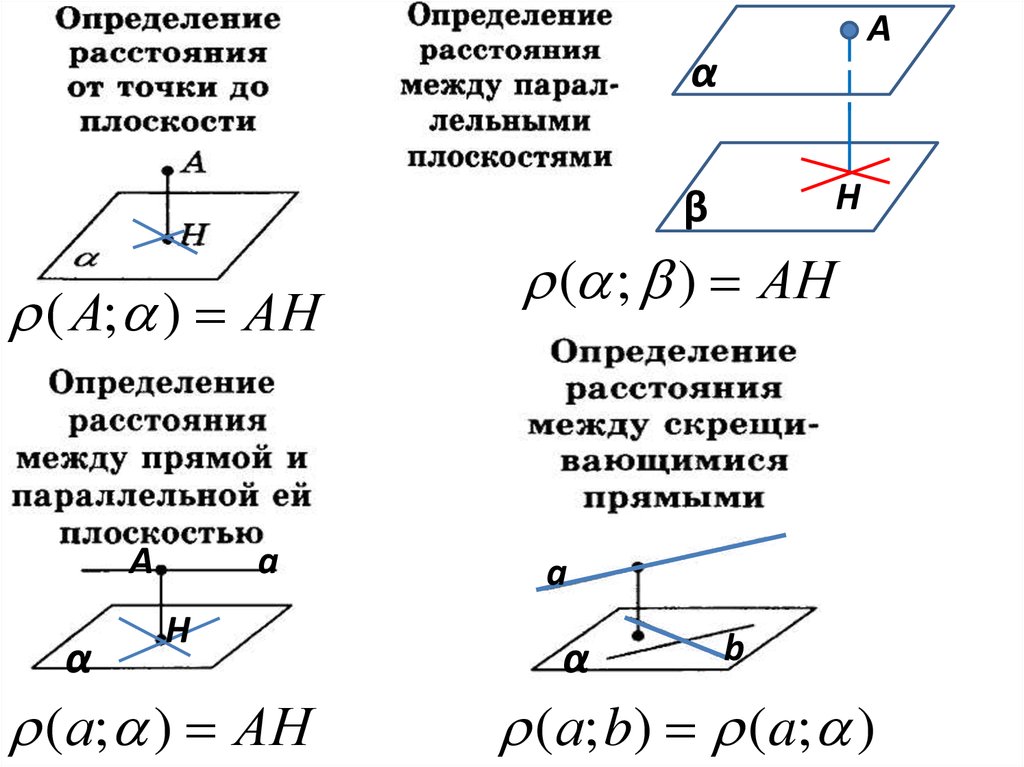
A
α
H
β
( А; ) АН
A
α
a
H
(а; ) АН
( ; ) АН
a
α
b
(а; b) (a; )

5.

Теорема о трёх перпендикулярах
Т8
А
А
Т9
a
α
Н
a
К
α
Н
Угол между прямой и плоскостью
a
α
К

6.

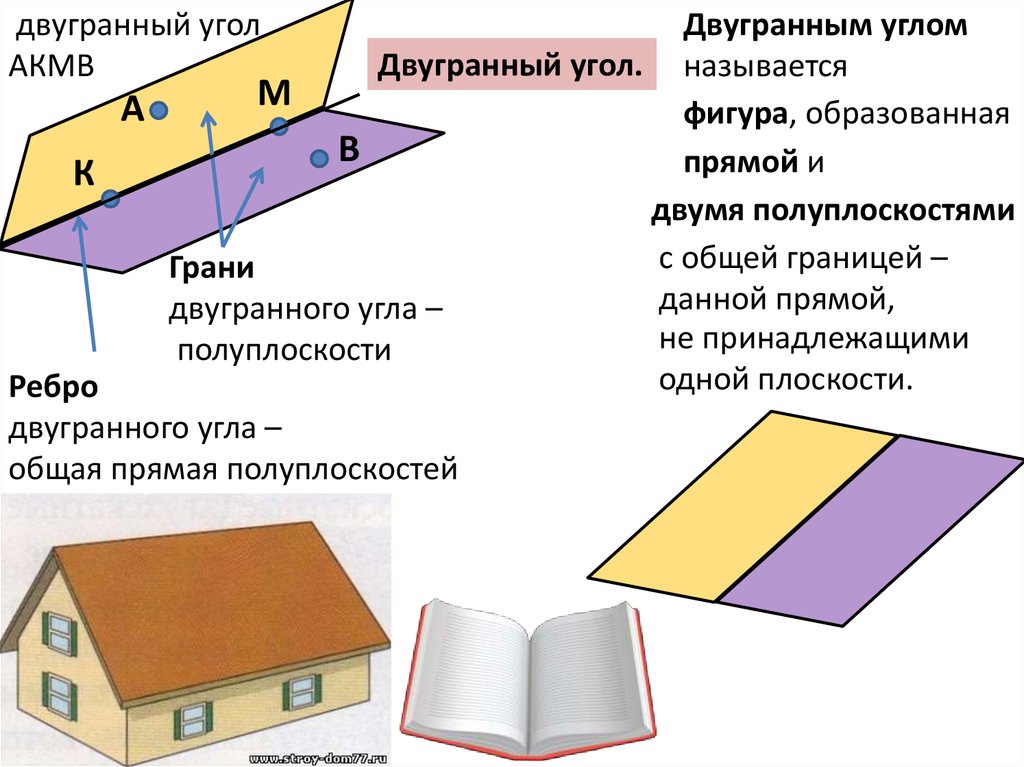
двугранный угол
АКМВ
Двугранным углом
Двугранный угол. называется
М
А
фигура, образованная
В
прямой и
К
двумя полуплоскостями
с общей границей –
Грани
данной прямой,
двугранного угла –
не принадлежащими
полуплоскости
одной плоскости.
Ребро
двугранного угла –
общая прямая полуплоскостей

7.

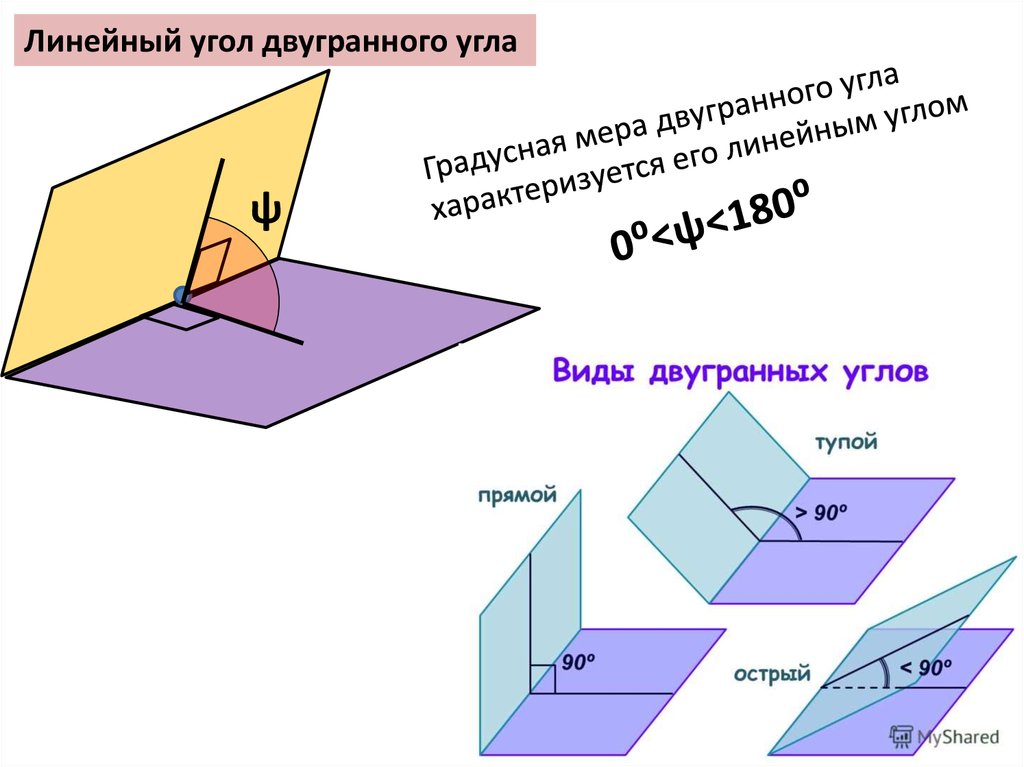
Линейный угол двугранного угла
ψ

8.

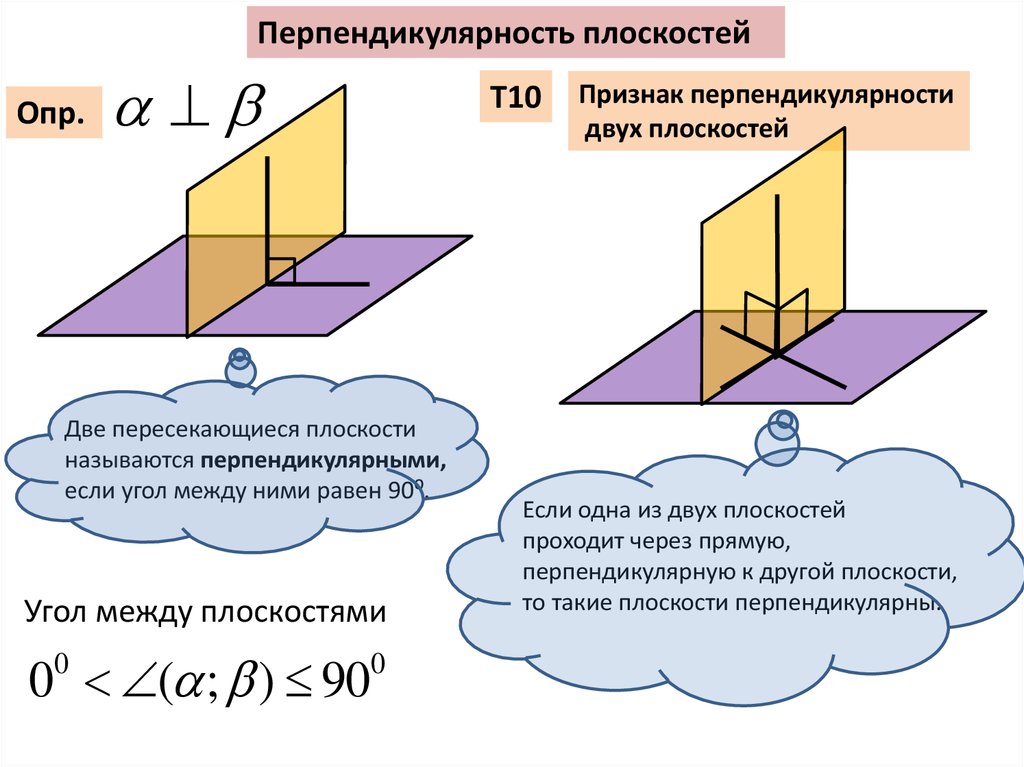
Перпендикулярность плоскостей
Опр.
Т10
Две пересекающиеся плоскости
называются перпендикулярными,
если угол между ними равен 90⁰.
Угол между плоскостями
0 ( ; ) 90
0
0
Признак перпендикулярности
двух плоскостей
Если одна из двух плоскостей
проходит через прямую,
перпендикулярную к другой плоскости,
то такие плоскости перпендикулярны.

9.

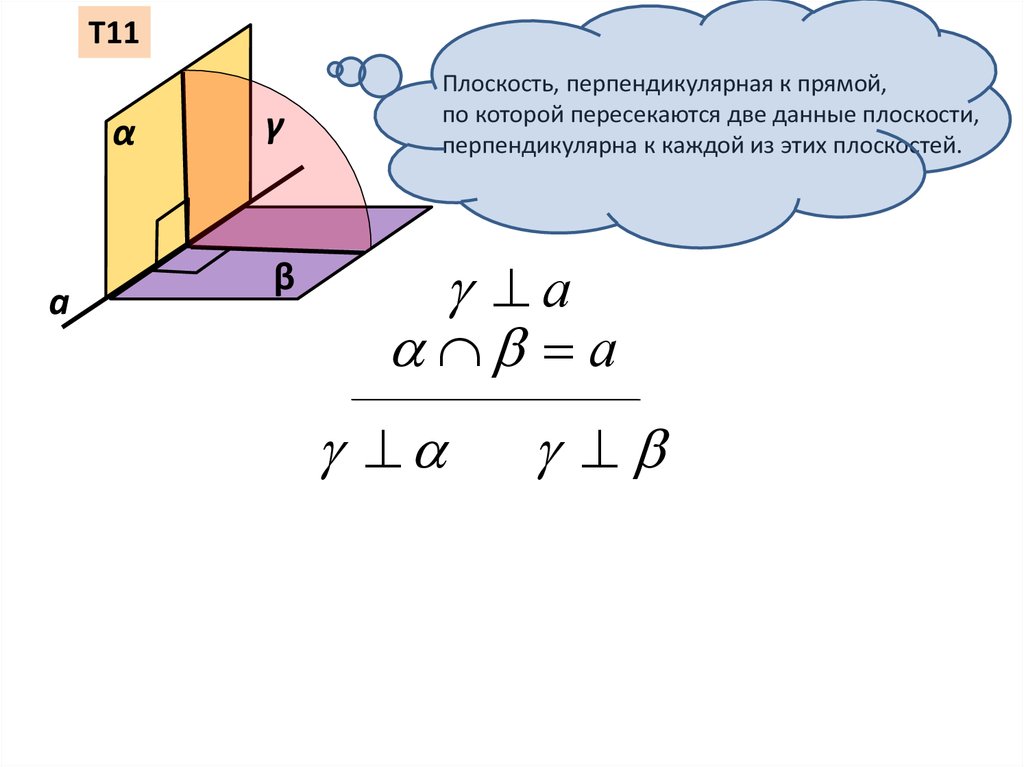
Т11
α
а
γ
β
Плоскость, перпендикулярная к прямой,
по которой пересекаются две данные плоскости,
перпендикулярна к каждой из этих плоскостей.
а
а

10.

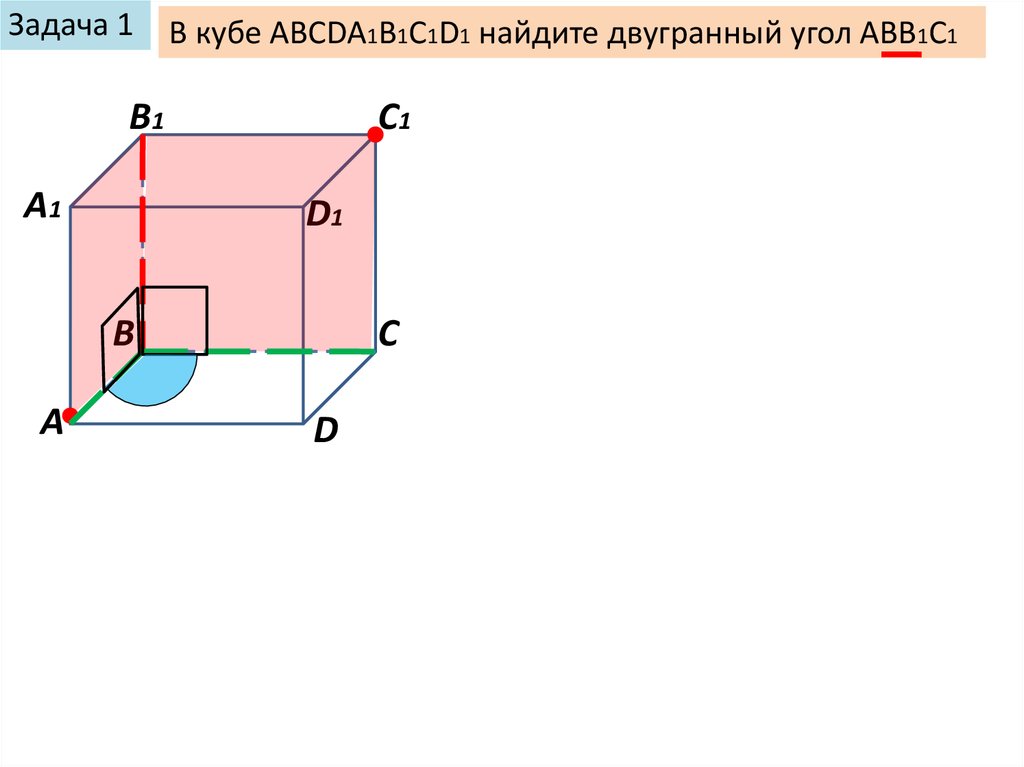
Задача 1
В кубе ABCDA1B1C1D1 найдите двугранный угол АВВ1С1
B1
А1
C1
D1
В
А
С
D

11.

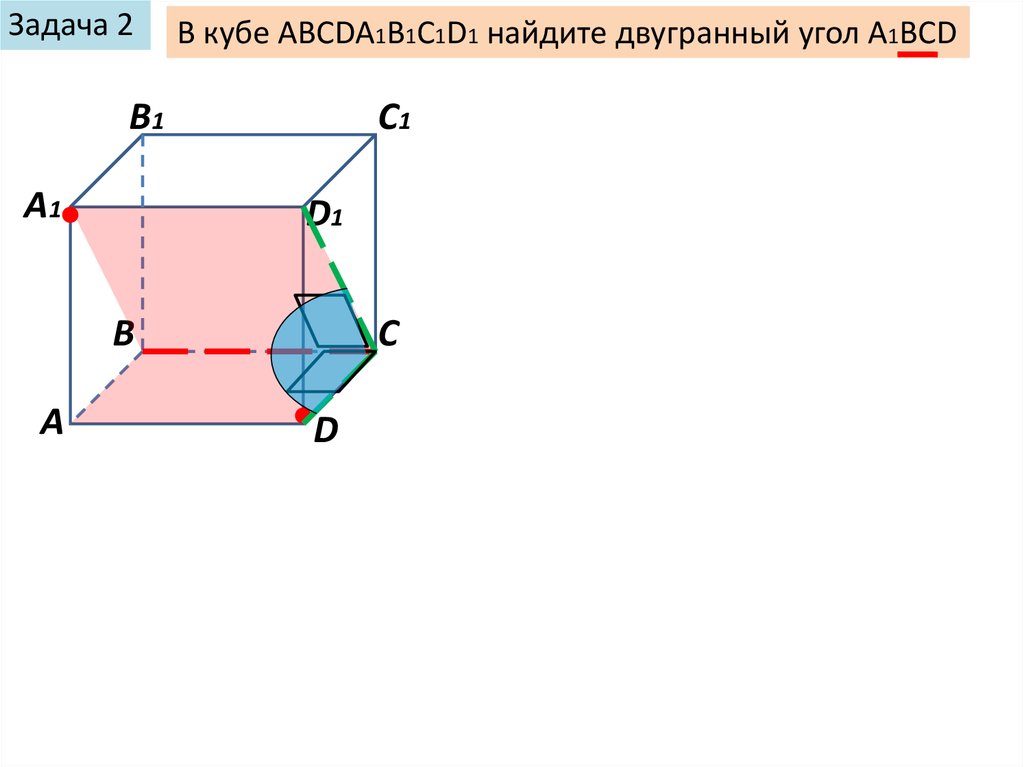
Задача 2
В кубе ABCDA1B1C1D1 найдите двугранный угол А1ВСD
B1
А1
C1
D1
В
А
С
D

12.

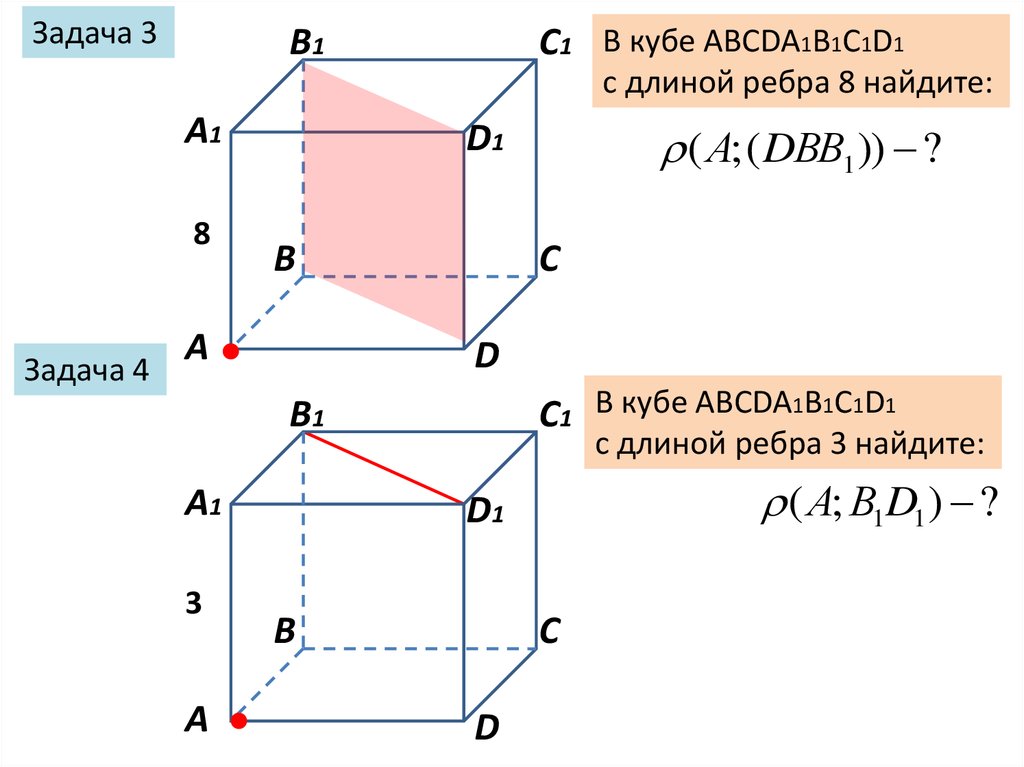
Задача 3
B1
C1 В кубе ABCDA1B1C1D1
с длиной ребра 8 найдите:
А1
8
Задача 4
В
А
С
D
C1 В кубе ABCDA1B1C1D1
B1
А1
3
А
( А; ( DВВ1 )) ?
D1
с длиной ребра 3 найдите:
( А; В1D1 ) ?
D1
В
С
D

13.

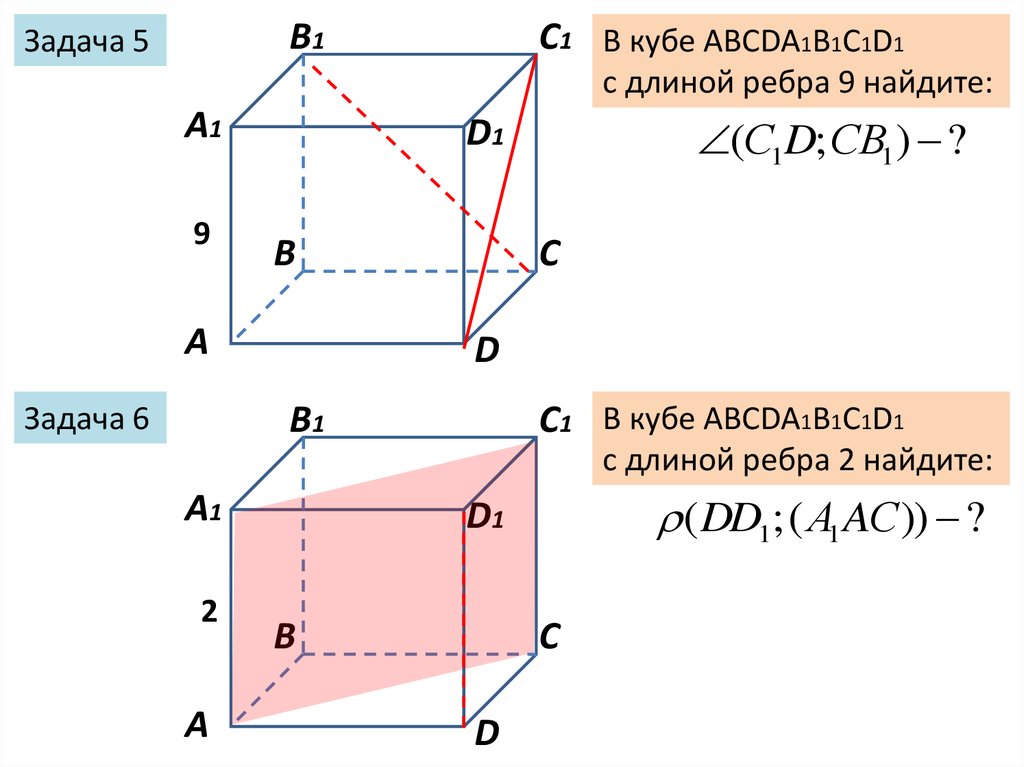
B1
Задача 5
C1 В кубе ABCDA1B1C1D1
с длиной ребра 9 найдите:
А1
9
В
А
С
D
B1
Задача 6
(С1D; СВ1 ) ?
D1
C1 В кубе ABCDA1B1C1D1
с длиной ребра 2 найдите:
А1
2
А
( DD1; ( А1 AС)) ?
D1
В
С
D

14.

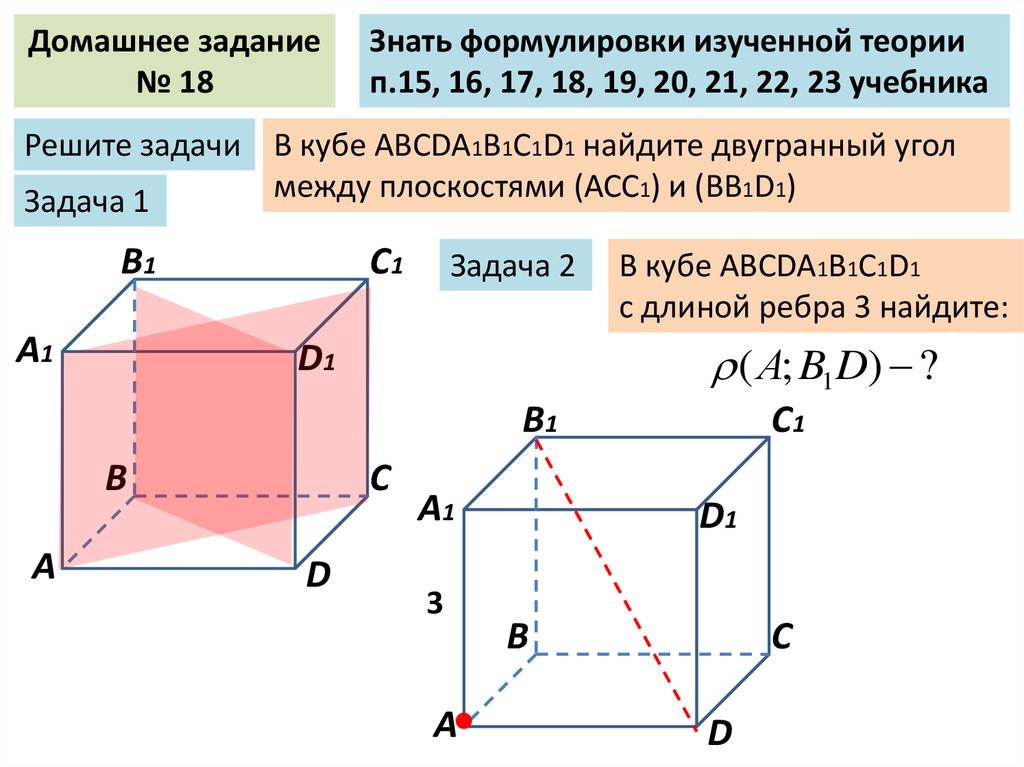
Домашнее задание
№ 18
Знать формулировки изученной теории
п.15, 16, 17, 18, 19, 20, 21, 22, 23 учебника
Решите задачи В кубе ABCDA1B1C1D1 найдите двугранный угол
между плоскостями (АСС1) и (ВВ1D1)
Задача 1
B1
А1
C1
Задача 2
В кубе ABCDA1B1C1D1
с длиной ребра 3 найдите:
( А; B1D) ?
D1
B1
В
А
С
D
А1
3
А
C1
D1
В
С
D

15.

B1
Задача 3
C1 В кубе ABCDA1B1C1D1
с длиной ребра 6 найдите:
А1
В
С
А
D
B1
Задача 4
А1
C1
D1
В
А
( B1; АC) ?
D1
(С1D; CВ) ?
С
D
В кубе ABCDA1B1C1D1
с длиной ребра 10 найдите: