Похожие презентации:
Решение геометрических задач при подготовке к ГИА
1.
Решениегеометрических задач
при подготовке
к ГИА
2.
Основные теоремы ,необходимые
для решения задач
на уроке:
3.
• о касательной;• о вписанном угле;
• об угле между касательной к
окружности и хордой;
• об отрезках касательных;
• признаки подобия треугольников;
• о биссектрисе угла в трапеции
(параллелограмме);
• о центре вписанной окружности в
угол, в треугольник.
4.
• о касательной;• о вписанном угле;
• об угле между касательной к
окружности и хордой;
Р
К
О
F
А
1
ОАМ ОА
2
М
5.
• признаки подобия треугольников;К
С
О
А
6.
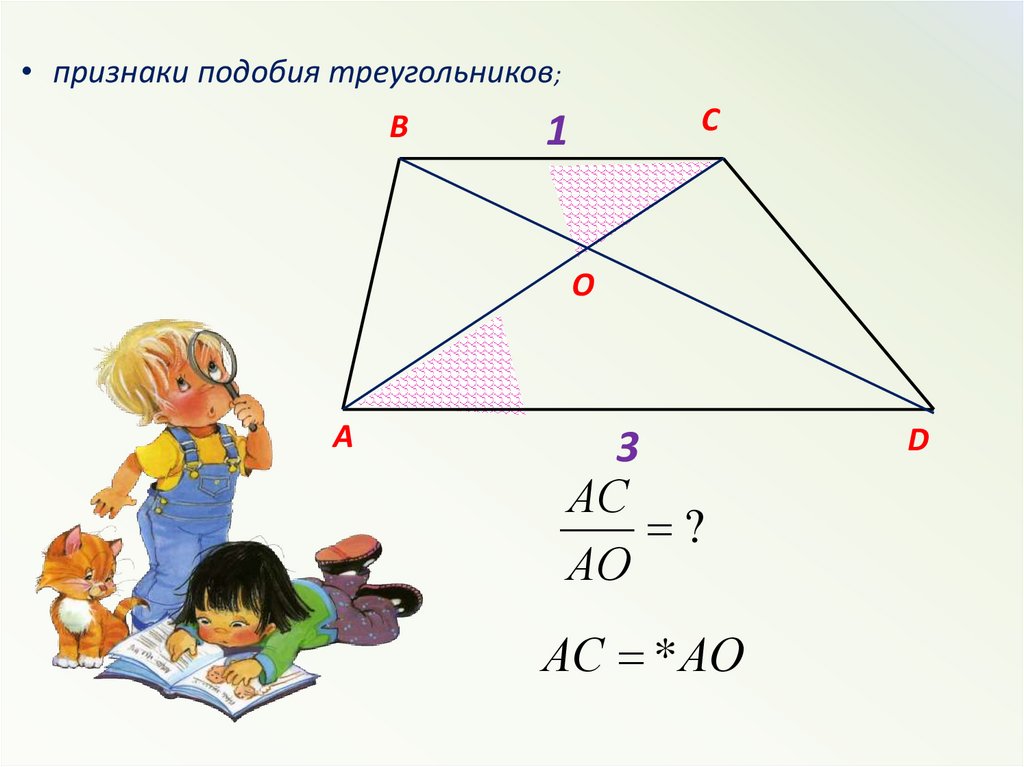
• признаки подобия треугольников;В
С
1
О
А
3
АС
?
АО
АС * АО
D
7.
• об отрезках касательных;О
А
М
D
8.
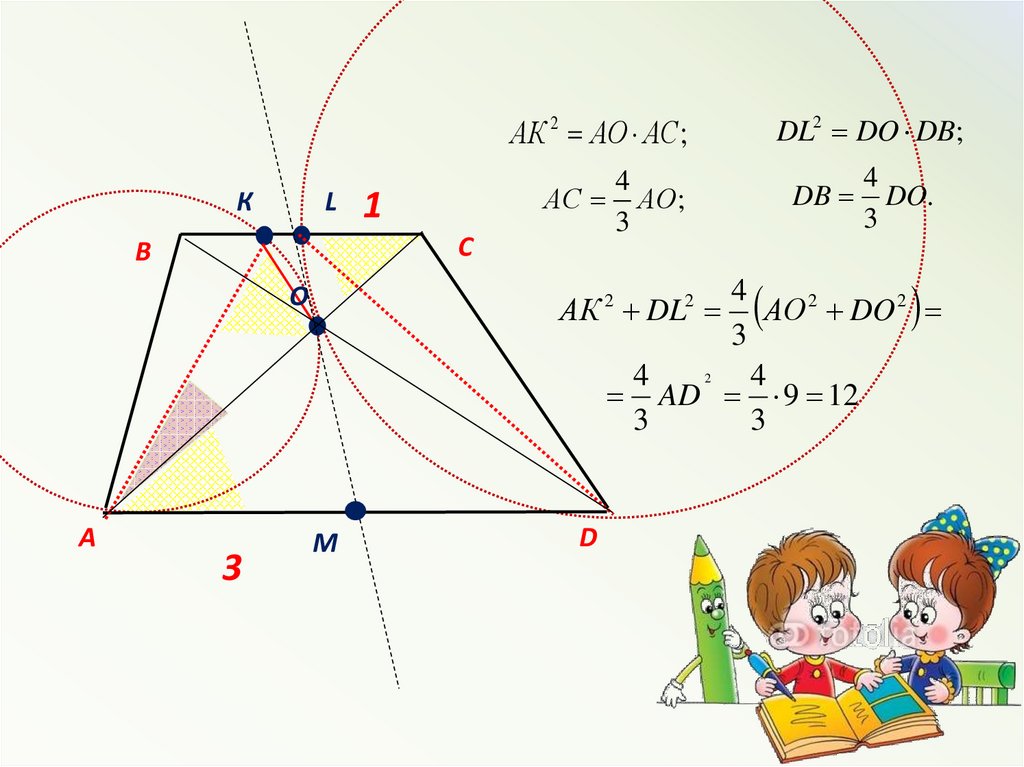
Задача №1Диагонали трапеции АВСD с
основаниями
АD=3
и
ВС=1
пересекаются в точке О. Две
окружности,
пересекающие
основание ВС в точках К и L
соответственно, касаются друг
друга в точке О, а прямой АD в
точках А и D соответственно.
Найдите АК2+DL2.
9.
DL2 DO DB;АК 2 АО АС ;
К
L
С
В
3
4
АК DL АО 2 DO 2
3
2
4
4
AD 9 12
3
3
О
А
1
4
DB DO.
3
4
АС АО;
3
2
M
D
2
10.
• о биссектрисе угла втрапеции (параллелограмме);
M
В
А
С
D
11.
• о центре вписаннойокружности в угол, в
треугольник.
В
N
С
О
М
K
А
12.
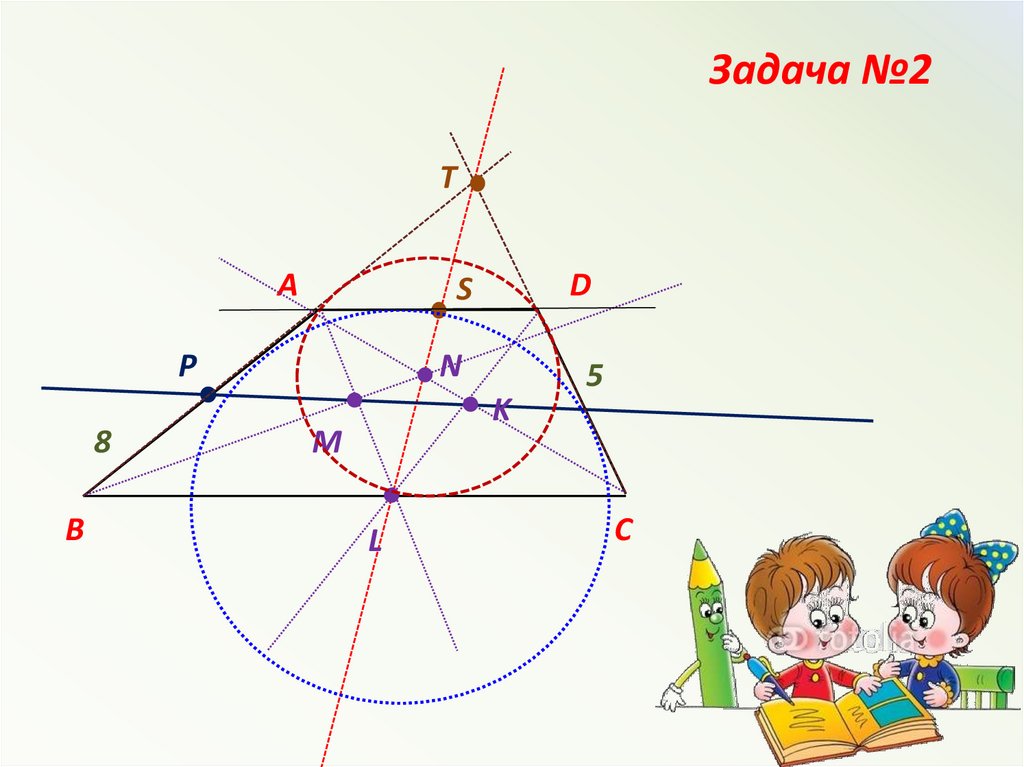
Задача №2В трапеции АВСD с боковыми
сторонами АВ=8 и СD=5 биссектриса
угла В пересекает биссектрисы углов А
и С в точках M и N соответственно, а
биссектриса угла D пересекает те же
две биссектрисы в точках L и K, причем
L лежит на основании ВС. В каком
отношении прямая МК делит сторону
АВ, а прямая LN – сторону АD?
13.
Задача №2T
А
P
8
В
D
S
N
K
M
L
5
С
5
14.
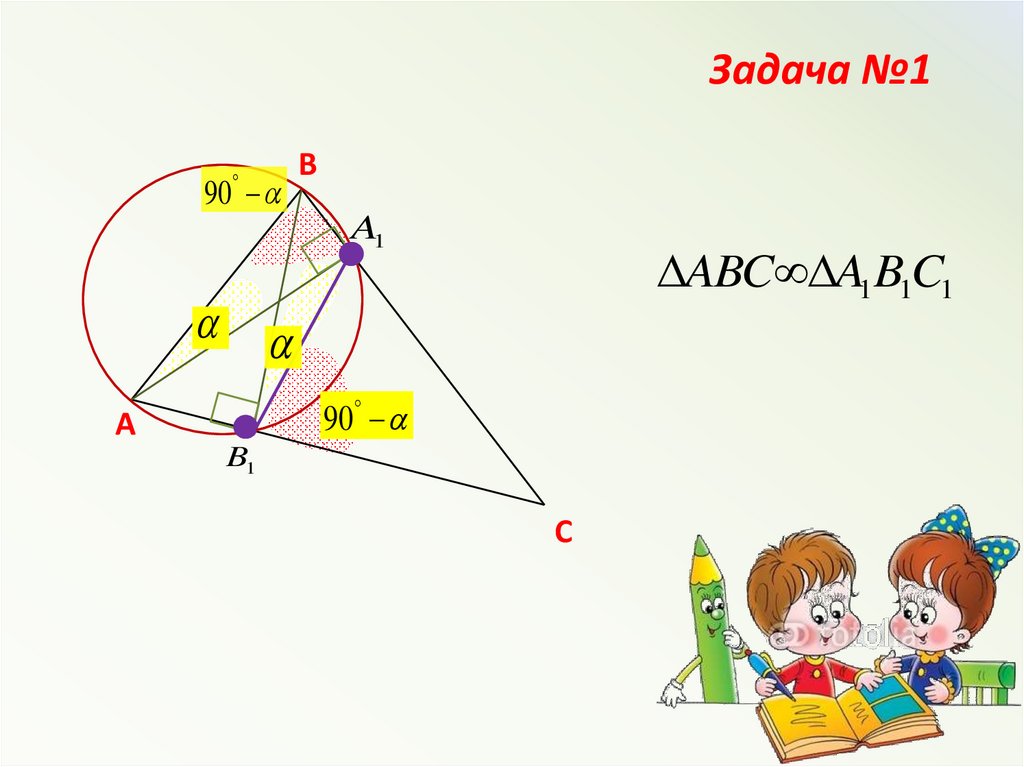
Задача №3Пусть АВС – остроугольный
треугольник, АА1 и ВВ1 – его
высоты, точка А1 лежит на
стороне ВС, точка В1 – на АС.
Доказать, что треугольник
А1В1С подобен треугольнику
АВС.
15.
Задача №190
B
A1
ABC A1B1C1
90
A
B1
C
16.
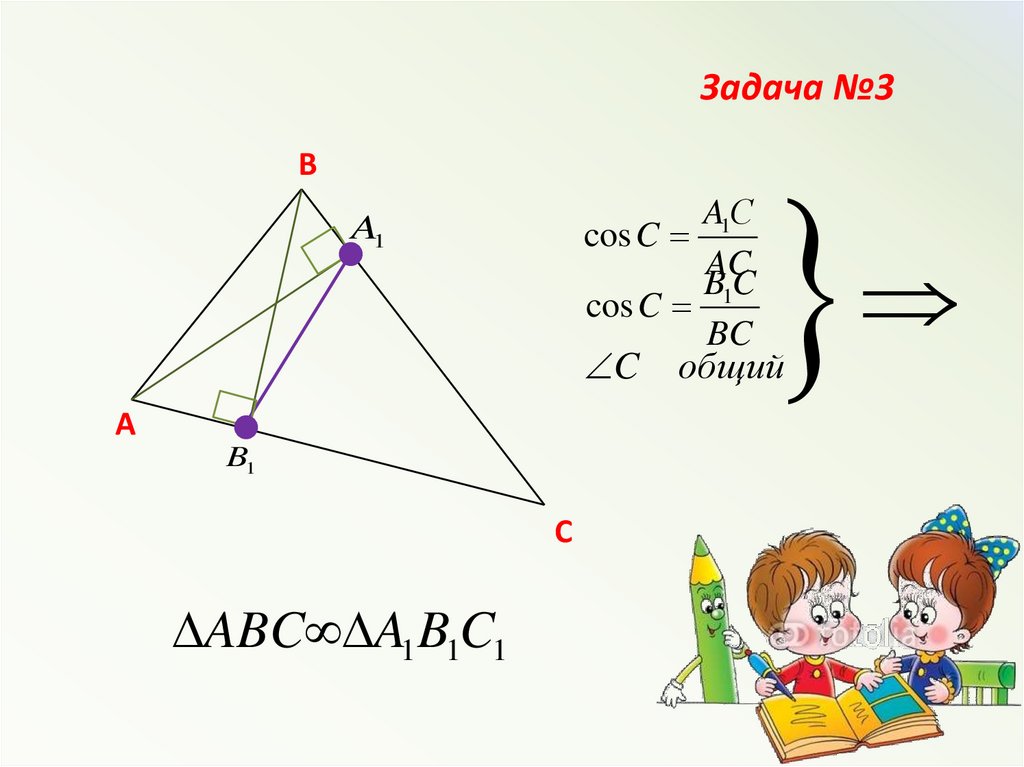
Задача №3B
A1С
cos C
AC
B1C
cos C
BC
A1
C общий
A
B1
C
ABC A1 B1C1
17.
Спасибо за урок18.
Задача №1Диагонали трапеции АВСD с основаниями АD=3 и ВС=1 пересекаются в точке О. Две окружности,
пересекающие основание ВС в точках К и L соответственно, касаются друг друга в точке О, а прямой
АD в точках А и D соответственно. Найдите АК2+DL2.
План решения задачи:
Найти на рисунке углы равные углу АКО;
Найти пару подобных треугольников, в которых одной из сторон является отрезок АК;
Составить соотношения сходственных сторон и выразить из этого соотношения АК2 (1);
Определить соотношение между множителями равенства (1), используя подобие другой пары
подобных треугольников, преобразовать это равенство;
Аналогично рассуждая, выразить DL2;
Составить сумму АК2+DL2
Доказать, что АО2+DO2=AD2;
С учетом пункта 7 подставить в выражение пункта 6 числовые значения, выполнить действия,
записать ответ.
Задача №2
В трапеции АВСD с боковыми сторонами АВ=8 и СD=5 биссектриса угла В пересекает биссектрисы
углов А и С в точках M и N соответственно, а биссектриса угла D пересекает те же две биссектрисы в
точках L и K, причем L лежит на основании ВС. В каком отношении прямая МК делит сторону АВ, а
прямая LN – сторону АD?












 Математика
Математика








