Похожие презентации:
Випадковий вектор. Граничні теореми теорії ймовірності
1.
Розділ 1. Основи теорії ймовірностейТема 8. Випадковий вектор. Граничні теореми
теорії ймовірності.
2.
1. Двовимірний випадковий вектор.2. Дискретний випадковий вектор,
закон розподілу, числові
характеристики.
3. Кореляційний момент, коефіцієнт
кореляції.
3.
Системою n ВВ називаєтьсявпорядкований набір n ВВ
(Х1, Х2, … ,Хi, … ,Хn )
Хi – компоненти системи
Інші назви:
n – вимірна ВВ
n – вимірний випадковий вектор
4.
Можливі значення (реалізації) системи nВВ позначаються так:
x1 , x2 , ..., xi ,...xn
(Х1, Х2 ) -
двовимірна ВВ
(усі її реалізації можна зобразити на
площині Х1оХ2 )
5.
Системи n ВВ поділяються на1. Дискретні (якщо компоненти дискр.)
2.Неперервні (якщо компоненти неп.)
6. Закон розподілу системи n ВВ
Законом розподілу (ЗР) системи n ВВназивається будь-яке співвідношення
між реалізаціями системи та
відповідними їм імовірностями
ЗР системи має різні форми
Найпростіша форма – для дискретних
систем (таблиця)
7.
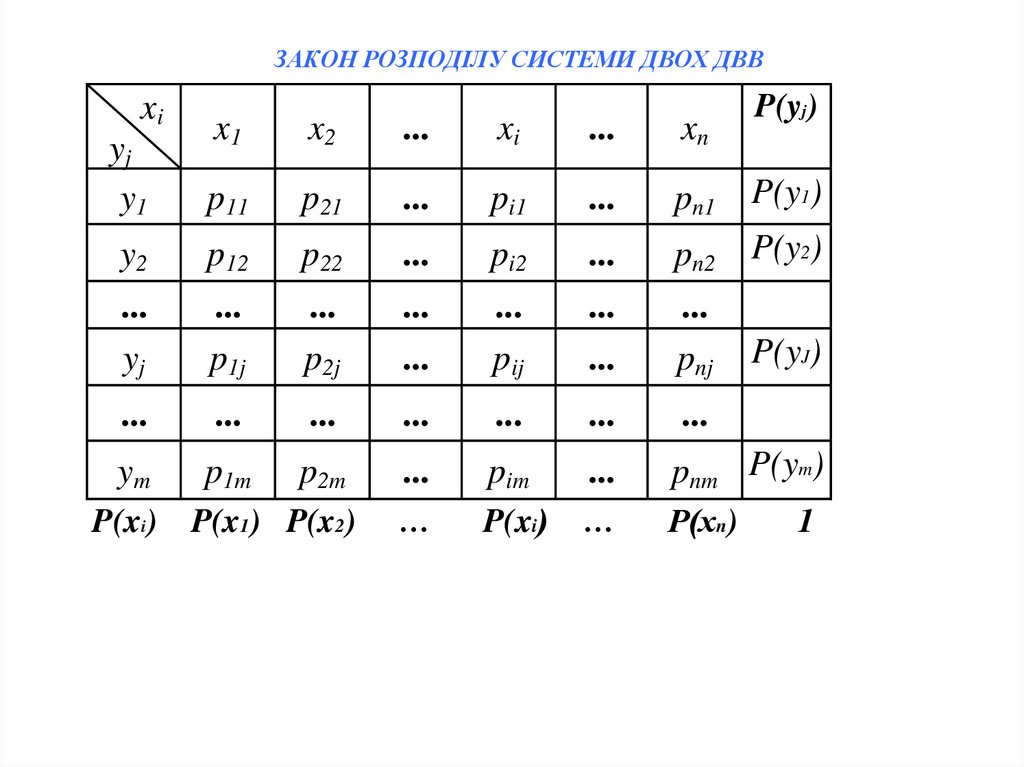
ЗАКОН РОЗПОДІЛУ СИСТЕМИ ДВОХ ДВВxi
P(yj)
yj
y1
x1
x2
...
xi
...
xn
p11
p21
...
pi1
...
y2
...
yj
p12
...
p1j
p22
...
p2j
...
...
...
pi2
...
pij
...
...
...
pn1 P(y1)
pn2 P(y2)
...
...
...
...
...
...
...
ym
p1m
p2m
...
pim
...
pnm P(ym)
…
P(xi) …
P(xi)
P(x1) P(x2)
...
pnj
P(xn)
P(yJ)
1
8.
Універсальна форма ЗР системифункція розподілу(як для дискретної так і для неперевної
системи)
Щільність розподілу імовірностей
(тільки для неперевної системи)
9.
Функція розподілу СВВn
F x1 , x2 , , xi , , xn P X i xi
i 1
F x, y P X x Y y
Геометричне зображення
y
x, y
X<x, Y<y
x
10. Властивості F(x, y)
1.11. Щільність імовірностей системи n НВВ
F ( x1 , x2 , ..., xi , ..., xn )f ( x1 , x2 , ..., xi , ..., xn )
x1 x2 ... xi ... xn
n
F ( x1 , x2 )
f ( x1 , x2 )
x1 x2
2
12. Властивості f(x, y)
1. f(x, y)0
2.
f ( x, y) dx dy 1
- умова норм.
bd
3. P ( a X b, c Y d ) f ( x, y ) dx dy
ac
P( ( x, y ) D) f ( x, y ) dx dy
( D)
13.
x4.
y
F ( x, y ) f ( x, y ) dx dy
5.
f1 ( x) f ( x, y ) dy
f 2 ( y ) f ( x, y ) dx
14. Умова незалежності ВВ
Дві ВВ наз незалежними, якщо ЗРкожної з них не залежить від того,
яких значень набуде інша
15.
Незалежність двох ДВВ X та Y, щовходять до системи, рівносильна
P(xi, yj ) = P(xi ) P( yj )
Незалежність двох ДВВ та НВВ X та Y,
що входять до системи, рівносильна
F(x, y ) = F1(x ) F2( y)
16.
Незалежність двох НВВ X та Y, щовходять до системи, рівносильна
f(x, y ) = f1(x ) f2( y)
17.
Якщо дві ВВ X та Y, що входять досистеми, незалежні, то, знаючи ЗР
окремих ВВ, можна знайти ЗР системи.
Якщо дві ВВ X та Y, що входять до
системи, залежні, то попередні
співвідношення не виконуються.
18.
4. Умовні закони розподілу системидвох випадкових величин
19.
НАГАДУЮ!!!Дві ВВ наз залежними, якщо ЗР
кожної з них залежить від того, яких
значень набуде інша
20. Дискретний випадок
P(xi /yj ) – імовірність того, що ВВ Хнабуде значення хi , за умови,
що ВВ Y набуде значення уj
(Умовна ймовірність ВВ Х)
P(yj /xi ) – імовірність того, що ВВ Y
набуде значення уj , за умови,
що ВВ X набуде значення хi
(Умовна ймовірність ВВ Y)
21. Умовні ймовірності обчислюються за формулами
P ( xi / y j )P( xi , y j )
P ( y j / xi )
P( xi , y j )
P( y j )
P ( xi )
22.
Умовним ЗР ДВВ Х за фіксованогозначення Y = yj називають
співвідношення між усіма можливими
значеннями ДВВ Х та відповідними їм
умовними імовірностями P(xi /yj )
Х=хi
P(xi /yj )
x1
x2
P(x1 /yj ) P(x2 /yj )
n
…
xn
…
P(xn /yj )
P( xi / y j ) 1
i 1
23.
Аналогічно визначається умовнийЗР ДВВ Y за фіксованого значення
X = xi
24. Таким чином, можна знайти ЗР системи двох залежних ДВВ, якщо знати умовні та безумовні розподіли компонент
P( xi , y j ) P( y j ) P( xi / y j )P( xi , y j ) P( xi ) P( y j / xi )
25. Неперервний випадок (X, Y) – система двох НВВ f(x, y)-щільність імовірностей системи
f1 ( x) f ( x, y ) dyf 2 ( y ) f ( x, y ) dx
26.
Умовною щільністю імовірностейНВВ, що входить до системи, за
фіксованого значення іншої НВВ
називають наступні співвідношення
f ( x, y )
f ( x / y)
f 2 ( y)
f ( x, y )
f ( y / x)
f1 ( x)
27. З попередніх формул
f ( x, y ) f 2 ( y ) f ( x / y )f ( x, y ) f1 ( x) f ( y / x)
28.
5. Числові характеристики СВВ29. Для (X, Y) Дискретний випадок
1. (mx , m y ) мат. сподівання системиn
m
mx xi p( xi )
m y y j p( y j )
i 1
j 1
2. ( Dx , Dy ) дисперсія системи
n
Dx x p( xi ) m
i 1
2
i
m
2
x
Dy y j p( y j ) m
2
j 1
3. ( x , y ) с. к. в. системи
x Dx
y Dy
2
y
30. Для (X, Y) Неперервний випадок
Для (X, Y)1.
Неперервний випадок
(mx , m y ) мат спод системи
mx xf1 x dx
2.
m y yf 2 y dy
( Dx , Dy ) дисп системи
Dx x f1 x dx m
2
2
x
Dy y f 2 y dy m
2
3. ( x , y ) с. к. в. системи
x Dx
y Dy
2
y
31. Нова ЧХ, яка характеризує взаємозв’язок між ВВ в системі Кореляційний момент (коваріація)
K xy M ( X mx )(Y m y ) Cov( xy)Має вимірність : вим Х на вим У
Характеризує
а ) ступінь залежності ВВ
б ) розсіюванн я навколо точки (mx m y )
на площині
32. Дискретний випадок
nm
K xy ( xi mx )( y j m y ) pij
i 1 j 1
n
m
K xy xi y j pij mx m y
i 1 j 1
33. Для (X, Y) Неперервний випадок Кореляційний момент (коваріація)
K xy ( x mx )( y m y ) f ( x, y ) dxdyK xy x yf ( x, y )dxdy mx m y
34. Коефіцієнт кореляції (характеризує тільки ступінь тісноти лінійної залежності між ВВ)
rxyK xy
x y
1 rxy 1
(вставка 2)
35.
rxy 1 - зв’язок між змінними лінійнийrxy 1 - зв’язок між змінними лінійний
rxy 0
-лінійного зв’язку між змінними
х та у немає взагалі або він дуже
слабкий
36. Означення
Дві ВВ Х та У наз корельованими,якщо кореляційний момент Кху 0
(r 0 )
xy
Дві ВВ Х та У наз некорельованими,
якщо кореляційний момент Кху = 0
(r 0 )
xy
37.
Дві корельовані ВВ є також залежними.Обернене твердження правильне не
завжди:
якщо дві ВВ залежні, то вони можуть
бути як корельованими так і
некорельованими











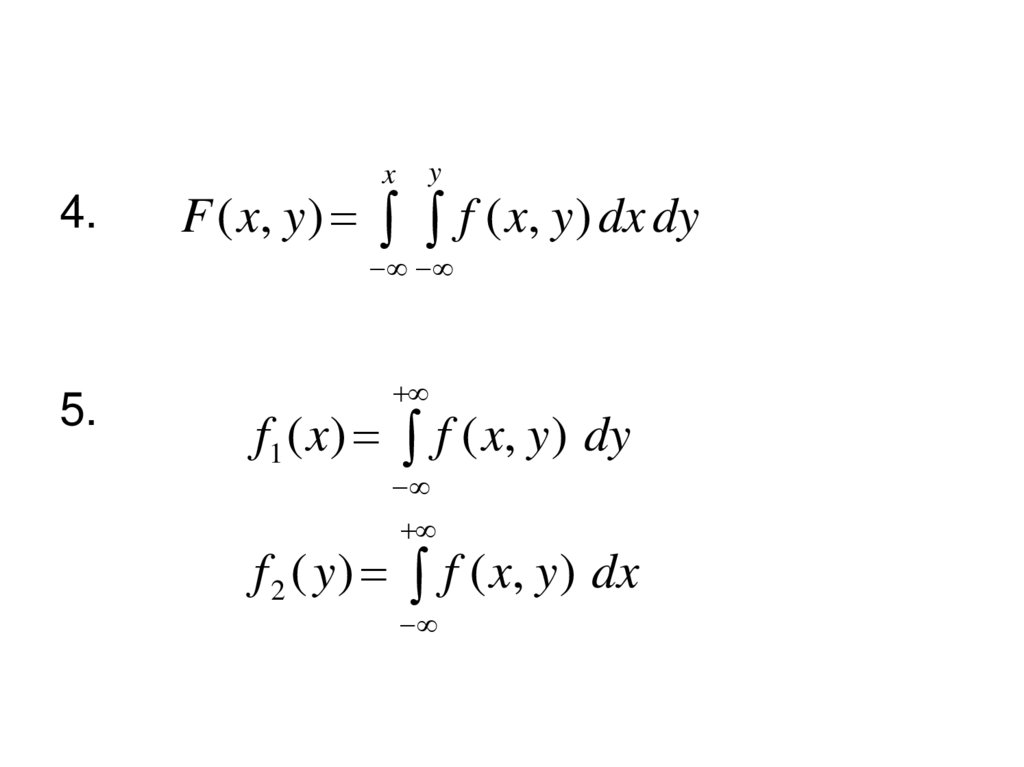
























 Математика
Математика








