Випадкові величини. Визначення випадкової величини (лекція 6)

1.

ВИПАДКОВІ ВЕЛИЧИНИ
Лекція 6

2. Визначення випадкової величини

• Випадкова величина – це величина, що
приймає в результаті випробування одне
з можливих значень, при цьому поява
того чи іншого значення є випадковою
подією.
• Розрізняють дискретні та неперервні
випадкові величини.

3. Дискретна випадкова величина та способи її задання

Дискретною випадковою величиною
називається випадкова величина з кінцевою
кількістю можливих значень.
• Для визначення дискретної випадкової величини
задають закон її розподілу (чи ряд розподілу),
тобто всі можливі значення випадкової
величини та відповідні їм ймовірності:

4. Дискретна випадкова величина та способи її задання

• Події, що полягають в тому, що з'явиться одне з
можливих значень випадкової величини, є несумісними й
утворюють повну групу подій. Сума ймовірностей повної
групи подій дорівнює одиниці:
Pi
n
Pi x 1
P3
P4
i 1
P2
P1
P5
P6
xi
0
x1 x2
x3
x4
x5
x6
Графічне зображення дискретної випадкової величини у вигляді
многокутника розподілу.

5. Числові характеристики дискретної випадкової величини

• Математичне сподівання
n
( X ) xi pi x1 p1 ... xn pn
i 1
• Дисперсія
D( X ) ( X ) ( ( X ))
2
, де ( X 2 ) xi2 Pi
n
2
• Середнє квадратичне відхилення
( X ) D( X )
i 1

6. Основні закони розподілу дискретних випадкових величин

• Формула Бернуллі:
Pn x
Cnx p x q n x
n!
p x q n x
x! n x !
P А p , P А q
• Сукупність отриманих ймовірностей Рn(0),
Рn(1), Рn(2), …,Рn(n) являє собою біномний
розподіл.

7. Основні закони розподілу дискретних випадкових величин

• Формулу Муавра-Лапласа використовують для
схеми Бернуллі, коли n 10 p 0,1
Ймовірності визначають за формулами:
а)
Pn ( X x)
1
e
2 npq
1 x np
2 npq
2
- локальна формула Лапласа;2
б) P ( x X x ) 1
n
1
2
2
z2 z
e 2
z1
x 2 np
x1 np
dz (
) (
)
npq
npq
- інтегральна формула Лапласа, де Ф(z)- інтегральна
функція Лапласа

8. Основні закони розподілу дискретних випадкових величин

• За тих же умов, але коли n 10
застосовують формулу Пуассона:
де np
Pn x
p 0,1
і
x
x!
• При цьому:
X D X ;
e
,

9. Неперервна випадкова величина. Способи її задання

• Неперервною випадковою величиною називається
випадкова величина, що може приймати будь-які
значення з деякого інтервалу (на якому вона існує).
• Інтегральна функція розподілу неперервної
x
випадкової величини:
F ( x) P( X x)
f ( x)dx
• Диференціальна функція розподілу неперервної
випадкової величини (функція щільності розподілу):
dP
f ( x)
F ( x)
dx

10. Неперервна випадкова величина

f(x)
Неперервна випадкова величина
x2
x1
0
x
Графічне задання неперервної випадкової
величини у вигляді функції розподілу щільності
ймовірностей.
F(x)
f ( x)dx 1
1
0
Умова нормування для
неперервної
випадкової величини :
1
2
3
4
5
x
Графічне зображення інтегральної функції розподілу
випадкової величини.

11. Числові характеристики неперервної випадкової величини

( X )
• Математичне сподівання:
x2
x f ( x )dx
x1
D( X ) ( X 2 ) ( ( X )) 2
• Дисперсія :
де
x2
( X 2 ) x 2 f ( x )dx
x1
• Середнє квадратичне відхилення :
( X ) D( X )
• Ймовірність попадання у проміжок :
P( x1 X x 2 )
x2
f ( x)dx F ( x2 ) F ( x1 )
x1

12. Основні закони розподілу неперервних випадкових величин

• 1. Рівномірний розподіл:
Диференціальна функція розподілу -
x a;
0,
1
f ( x)
, a x b;
b a
x b.
0,
Інтегральна функція розподілу -
x a;
0,
x a
F ( x)
, a x b;
b a
x b.
1,

13. Основні закони розподілу неперервних випадкових величин

• 2. Показниковий (експонентний)
розподіл неперервної випадкової величини з
параметром .
Диференціальна функція розподілу -
Інтегральна функція розподілу -
x 0;
0,
f ( x ) x
e , x 0.
x 0;
0,
F ( x) x
1 e , x 0.

14. Основні закони розподілу неперервних випадкових величин

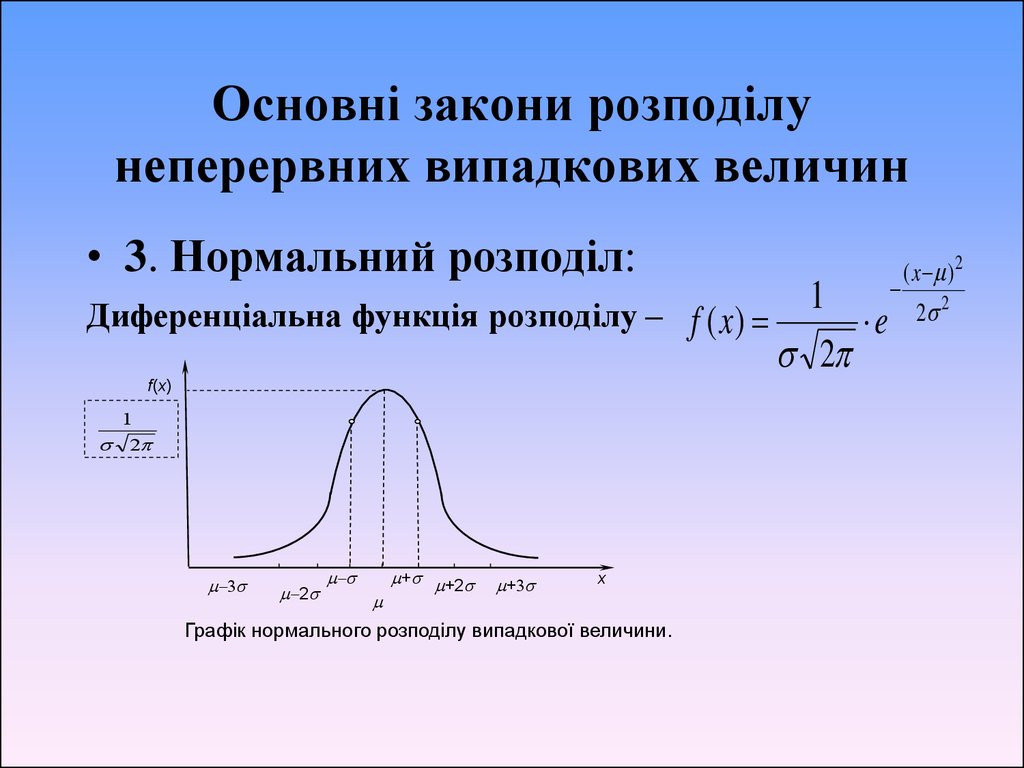
• 3. Нормальний розподіл:
1
Диференціальна функція розподілу – f ( x )
e
2
f(x)
1
2
2
+ +2
+
x
Графік нормального розподілу випадкової величини.
( x )2
2 2

15. Стандартна функція Лапласа

• Якщо в функції Гаусса взяти 0 і 1 , то
отримаємо нормовану або стандартну функцію
(диференціальну функцію ).
( z)
1
e
2
z2
2

16. Основні закони розподілу неперервних випадкових величин 3. Нормальний розподіл

• Ймовірність попадання нормально розподіленої
випадкової величини на інтервал визначається за
формулою:
x2
x1
P( x X x )
1
1
2
z
2
z2
e 2 dz
де
- інтегральна функція Лапласа,
її значення знаходяться за таблицею.
( z )
• Правило трьох сигм: якщо випадкова величина
нормально розподілена, то майже достовірно, тобто з
імовірністю, близької до одиниці , ії значення лежать
на проміжку [ .

17. ДЯКУЮ ЗА УВАГУ!